Dans le conseil du mois de novembre 2011 (TOTM), nous avons présenté les calculs du compresseur d’une étude de cas. Nous avons comparé les résultats de la méthode rigoureuse avec les valeurs des méthodes raccourcies. La méthode rigoureuse était basée sur une équation d’état comme celle de Soave-Redlich-Kwong (SRK) pour calculer les enthalpies et entropies requises. Ces enthalpies et entropies sont utilisées pour déterminer la puissance requise et les températures de décharge. Les résultats ont indiqué que la précision de la méthode de raccourci est sensible à la valeur du rapport de capacité thermique d’état de gaz idéal, k.
Du seul point de vue du calcul, le calcul de la puissance est particulièrement sensible à la spécification du débit massique, de la température et de la pression d’aspiration, et de la température et de la pression de refoulement. Un compresseur va fonctionner sous des valeurs variables des variables affectant ses performances. Ainsi, la partie la plus difficile du calcul d’un compresseur est la spécification d’une plage raisonnable pour chaque variable et non le calcul lui-même. La référence souligne que l’utilisation d’une seule valeur pour chaque variable n’est pas la bonne façon d’évaluer un système de compression.
Normalement, les calculs thermodynamiques sont effectués pour un processus idéal (réversible). Les résultats d’un processus réversible sont ensuite adaptés au monde réel par l’utilisation d’une efficacité thermodynamique. Dans le processus de compression, il existe trois processus idéaux qui peuvent être visualisés : 1) un processus isotherme (PV1=C1), 2) un processus isentropique (PVk=C2) et 3) un processus polytropique (PVn=C3). Chacun de ces processus peut être utilisé de manière appropriée comme base pour évaluer les besoins en puissance de compression, que ce soit par calcul manuel ou informatique. Le processus isotherme, cependant, est rarement utilisé comme base parce que le processus de compression industriel normal n’est même pas approximativement effectué à température constante.
Notez que Dresser Rand fait pas mal de travail avec la compression à « température presque constante », en particulier pour la compression du CO2 à partir de cheminées d’évent. Pour plus de détails, référez-vous à :
Dans ce TOTM, nous allons démontrer comment déterminer l’efficacité d’un compresseur à partir du débit mesuré, de la composition, des températures et des pressions d’aspiration et de refoulement. Un calcul rigoureux basé sur une équation d’état et une méthode raccourcie sont envisagés et les résultats sont comparés.
Efficacité d’un compresseur
Les efficiencies des compresseurs varient selon le type, la taille et le débit du compresseur. Ils ne peuvent être déterminés (après coup) que par un test de compresseur, bien que les fabricants de compresseurs puissent généralement fournir de bonnes estimations. À des fins de planification, la référence suggère les valeurs suivantes pour les efficiencies globales:
Tableau 1. Efficacités globales des compresseurs
|
Type de compresseur |
Efficacité, η |
|
Centrifuge |
0.70 – 0,85 |
|
Spiral à grande vitesse |
0,72 – 0,85 |
|
Spiral à faible vitesse |
0.75 – 0,90 |
|
Vis rotative |
0,65 – 0,75 |
Les références indiquent que ces efficacités globales comprennent la friction des gaz à l’intérieur du compresseur, les pertes mécaniques (roulements, joints, boîte de vitesses, etc.) et les pertes de la boîte de vitesses. L’efficience mécanique varie selon la taille et le type de compresseur, mais 95 % est un chiffre de planification utile. Lors du calcul de la tête du compresseur et de la température de refoulement, l’efficience utilisée sera isentropique ou polytropique (l’efficience isentropique est parfois appelée efficience adiabatique). L’ajout de 3-4 % d’efficiences (pertes mécaniques) aux efficiences globales du tableau 1 donnera généralement une bonne estimation de l’efficience thermodynamique .
Pour évaluer la performance d’un compresseur existant, l’objectif est de calculer l’efficacité (η) du compresseur et la puissance requise.
Les propriétés connues et mesurées sont :
a. Débit volumique du gaz en condition standard (qS) ou débit massique du gaz ()
b. Composition du gaz (zi)
c. Pression d’aspiration (P1) et température (T1)
d. Pression de refoulement (P2) et température (T2)
Estimation de l’efficacité – Méthode rigoureuse
Le cœur de tout logiciel commercial de simulation de flux de processus est une équation d’état. En raison de leur simplicité et de leur relative précision, on utilise une EOS cubique telle que Soave Redlich-Kwong (SRK) ou Peng-Robinson. Ces équations sont utilisées pour calculer les équilibres vapeur-liquide (EVL), l’enthalpie (h) et l’entropie (s). Avec des coefficients d’interaction binaire appropriés, les résultats de simulation de processus de ces deux équations sont pratiquement les mêmes. Par conséquent, seule la SRK est utilisée dans ce travail.
Le rendement isentropique est défini par
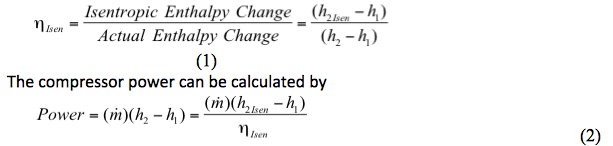
Où :
ηIsen = Rendement isentropique
h1 = Enthalpie d’aspiration calculée à P1, T1, et composition (zi)
h2 = Enthalpie de décharge calculée à P2, T2, et composition (zi)
h2Isen = Enthalpie de décharge isentropique à P2 (ou T2), S2Isen =S1, et composition (zi)
![]() = Débit massique
= Débit massique
Le calcul du rendement ou de la puissance du compresseur comporte deux étapes
1. Détermination de la variation d’enthalpie idéale ou isentropique (réversible et adiabatique) (h2Isen-h1) du processus de compression.
2. Détermination de la variation d’enthalpie réelle (h2-h1).
Le calcul étape par étape basé sur un EOS:
a. Supposer un état stationnaire, c’est-à-dire
b. Supposer que la composition de l’alimentation reste inchangée
c. Calculer l’enthalpie d’aspiration h1=f(P1, T1, et zi) et l’entropie s1=f(P1, T1, et zi) par EOS
d. Supposons un processus isentropique et fixons s2Isen = f (P2, T2Isen, zi) = s1 = f (P1, T1, zi).
e. Calculer l’enthalpie idéale (h2Isen) à la condition de décharge pour zi, T2 (ou P2) et s2Isen connus.
f. Calculer l’enthalpie réelle (h2) à la condition de décharge pour zi, T2 et P2 connus.
g. Calculer le rendement isentropique par l’équation 1 : µIsen = (h2Isen – h1)/(h2 – h1)
h. Calculer la puissance par l’équation 2 : ![]()
Estimation du rendement – Méthode raccourcie
L’exposant de la trajectoire isentropique (k) ou le rapport de capacité thermique du gaz idéal (k=CP/CV) peut être calculé par la corrélation présentée dans le TOTM de mai 2013 :
![]()
Où:
T = Température, K (°R)
![]() = Densité relative du gaz ; rapport du poids moléculaire du gaz au poids moléculaire de l’air
= Densité relative du gaz ; rapport du poids moléculaire du gaz au poids moléculaire de l’air
A = 0.000272 (0.000151)
La température de décharge réelle basée sur un trajet isentropique peut être estimée en

Solvant l’efficacité isentropique,
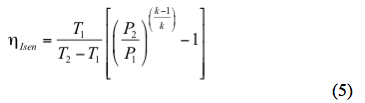
Similairement, la température de décharge réelle basée sur un chemin polytropique peut être estimée en

Solvant l’équation ci-dessus pour le coefficient de chemin polytropique (n) :

De même, la température de décharge réelle basée sur un chemin polytropique peut être estimée (ηPoly) par :

La tête isentropique est calculée par
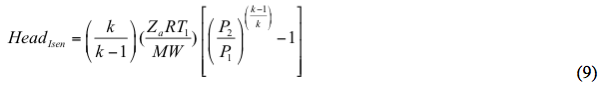
Similairement, la tête polytropique est calculée par
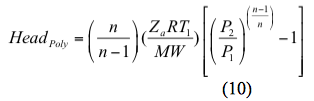
Pour un processus isentropique (réversible et adiabatique) la puissance est calculée par
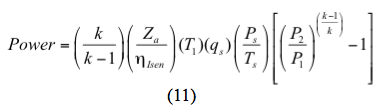
Ou pour un processus polytropique la puissance est calculée par
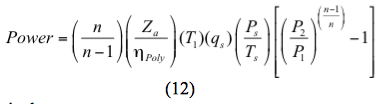
Alternativement :
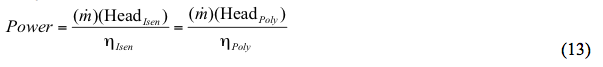
Où :
Head = Tête du compresseur, m (ft)
Power = Puissance du compresseur, kW (HP)
R = Constante universelle des gaz, 848 kg-m/(kmol-K) ou (1545 ft-lbf/(lbmol-°R))
PS = Pression de condition standard, kPa (psia)
P1 = Pression d’aspiration, kPa (psia)
P2 = Pression de refoulement, kPa (psia)
TS = Température de condition standard, K (°R)
T1 = Température d’aspiration, K (°R)
T2 = Température de refoulement, K (°R)
qS = Taux volumétrique du gaz à la condition standard, Sm3/d (scf/jour)
Za = Facteur de compressibilité moyen du gaz = (Z1+Z2)/2
Z1 = Facteur de compressibilité du gaz à l’état d’aspiration
Z2 = Facteur de compressibilité du gaz à l’état de refoulement
MW = Poids moléculaire du gaz
Le calcul de la puissance doit être effectué par étage de compression, puis additionné pour tous les étages reliés à un seul conducteur.
Le calcul pas à pas pour la méthode raccourcie
a. Calculer l’exposant isentropique (k) par l’équation 3 en utilisant la température moyenne définie par T = (T1+3T2)/4. Cette forme de température moyenne a été définie pour obtenir une meilleure correspondance entre les résultats de la méthode rigoureuse et ceux de la méthode raccourcie.
b. Calculer l’efficacité isentropique (ηIsen) par l’équation 5.
c. Calculer le coefficient polytropique (n) par l’équation 7.
d. Calculer l’efficacité polytropique (ηPoly) par l’équation 8.
e. Calculer les têtes isentropiques et polytropiques par les équations 9 et 10, respectivement.
f. Calculer la puissance requise par étage par l’équation 11 ou 12.
Etude de cas
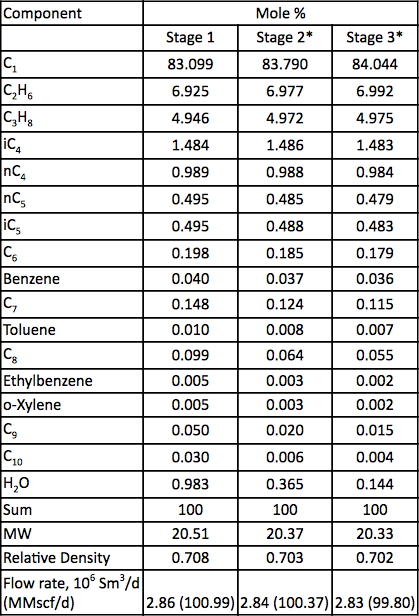
Un mélange de gaz naturel est comprimé à l’aide d’un compresseur centrifuge à trois étages. Le diagramme d’écoulement du processus est présenté à la figure 1. Pour chaque étage, la pression mesurée, et la température sont présentées dans le tableau 1. La composition de l’alimentation mesurée, les débits, et la masse moléculaire et la densité relative calculées sont présentés dans le tableau 2.
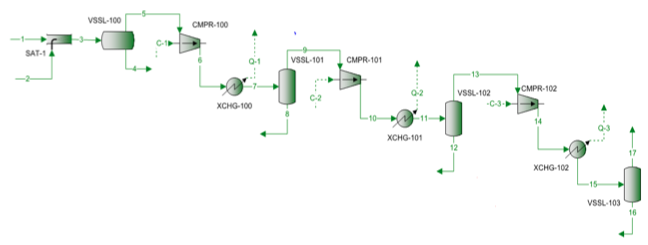
Figure 1. Diagramme d’écoulement du procédé pour une compression en trois étapes
Tableau 1. Température et pression mesurées pour les trois étapes de la compression
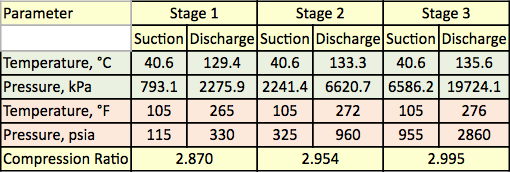
Tableau 2. Analyse des gaz et débit pour les trois étages de compression
* Calculés
Résultats et discussions
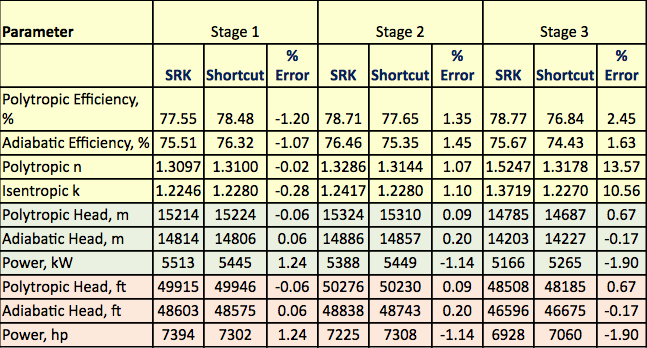
Le schéma de procédé présenté à la figure 1 a été simulé par le logiciel ProMax pour effectuer les calculs rigoureux à l’aide du SRK EOS. Le programme a calculé les rendements polytropiques et isentropiques, les têtes et la puissance de compression. Le programme a également calculé l’exposant de chemin isentropique (k), et l’exposant de chemin polytropique (n). Ces résultats calculés sont présentés dans le tableau 2 pour les trois étapes sous les intitulés SRK. Les calculs effectués par ProMax sont très similaires au pas à pas de a à h décrit dans la section rigoureuse. Le tableau 2 présente également les résultats des calculs raccourcis pour les valeurs correspondantes sous le titre raccourci. Les calculs raccourcis sont basés sur les étapes de a à f décrites dans la section sur la méthode raccourcie. Le pourcentage d’erreur entre la méthode rigoureuse et les méthodes raccourcies pour chaque étape est également présenté dans le tableau 2. Le tableau 2 indique que d’excellents accords sont obtenus pour les étapes 1 et 2. Cependant, des écarts plus importants sont observés pour les exposants isétropiques et polytropiques de l’étape 3 en raison de l’opération à haute pression qui s’est trop éloignée des conditions d’état gazeux idéal.
Tableau 3. Résumé des résultats calculés rigoureux et raccourcis
Conclusions
Le tableau 2 indique qu’il existe de bons accords entre les résultats raccourcis et les résultats rigoureux. Les différences entre les résultats de la méthode rigoureuse et ceux de la méthode raccourcie pour les calculs des installations et la planification sont négligeables. Pour l’étape 3, en raison du fonctionnement à haute pression et d’un écart trop important par rapport à la condition d’état gazeux idéal, une erreur plus importante est observée pour l’exposant isentropique (k).
L’exposant isentropique (k) calculé dans le ProMax n’est pas le rapport de capacité thermique (CP/CV) de l’état gazeux idéal. C’est la valeur de l’exposant isentropique qui est nécessaire pour donner un chemin isentropique de l’entrée à la sortie. Sa valeur est calculée comme une intégration de cette trajectoire. Il s’agit donc en quelque sorte d’une valeur « moyenne » représentant la véritable trajectoire isentropique. Pour les gaz idéaux, la valeur serait égale au rapport (CP/CV).
Cette erreur dans ‘k’ illustre également l’importance de spécifier quelle corrélation doit être utilisée lors de la commande d’un essai de performance (c’est-à-dire, se référer à ASME PTC-10 pour des détails supplémentaires), afin que le client et le fournisseur soient sur le même accord en allant de l’avant en ce qui concerne la masse moléculaire (MW) et k pour le fluide d’essai. Pour plus de détails, se référer à la référence et aux TOTM d’août et septembre 2010 .
Il peut également être utile de noter que lors de la tendance ‘n’ et de l’efficacité polytropique pour évaluer l’état de la machine, la précision relative des instruments/équipements de mesure (transducteurs de température et de pression) et la mise en correspondance des performances du compresseur avec la courbe de performance originale (débit volumique de gaz réel par rapport à la vitesse), introduit de nombreuses sources d’erreurs potentielles dans cette évaluation quotidienne.
Notez que la précision des méthodes raccourcies dépend des valeurs de k et de n. La définition de la température moyenne dans la méthode des raccourcis a été ajustée pour obtenir une meilleure correspondance entre l’exposant de chemin isentropique (k) calculé par la méthode rigoureuse.
Pour en savoir plus sur des cas similaires et sur la façon de minimiser les problèmes opérationnels, nous vous suggérons de participer à nos cours G4 (conditionnement et traitement du gaz), PF4 (installations de production et de traitement du pétrole), ME46 (systèmes de compression – conception mécanique et spécifications) et ME44 (principes fondamentaux des systèmes de pompes et de compresseurs).
PetroSkills offre une expertise de conseil sur ce sujet et bien d’autres. Pour plus d’informations sur ces services, visitez notre site Web à http://petroskills.com/consulting, ou envoyez-nous un courriel à [email protected].
Dr. Mahmood Moshfeghian
Référence:
3. Soave, G., Chem. Eng. Sci., Vol. 27, pp. 1197-1203, 1972.
4. Peng, D. Y., et Robinson, D. B., Ind. Eng. Chem. Fundam. vol. 15, p. 59, 1976.
5. ProMax 3.2, Bryan Research and Engineering, Inc, Bryan, Texas, 2014.
6. ASME PTC-10, « Code d’essai de performance sur les compresseurs et les expulseurs », 1997.
7. Honeywell, J. « Aspects importants des essais de compresseurs centrifuges – Partie 1 », Conseil du mois, août 2010
8. Honeywell, J. « Aspects importants des essais de compresseurs centrifuges – Partie 2 », Conseil du mois, septembre 2010
.