Ce qui suit est mon point de vue sur certains problèmes de mathématiques de soi-disant « common core math » ou « new math » qui ont circulé sur Internet. Je pense qu’ils nous montrent une mise en œuvre mal orientée du CCS.

Gardez à l’esprit que tout ce que vous voyez dans les livres de mathématiques ou sur Internet n’est pas correctement fait sur la base du CCS. Dans certains des exemples que vous voyez, il semble que les gens jettent le bon sens quand ils font des problèmes de mathématiques pour répondre aux normes du socle commun !

Je ne suis pas surpris que la mise en œuvre ait fini par être « bâclée » dans certains endroits. Les CCS sont un tel changement pour la plupart des enseignants qu’ils ont besoin de beaucoup de soutien et de rééducation avant de devoir enseigner selon ces normes.

J’ai toujours pensé que le principal problème auquel est confronté l’enseignement des mathématiques dans les classes élémentaires des écoles publiques est que de nombreux enseignants du primaire ne comprennent pas suffisamment les mathématiques pour pouvoir les enseigner correctement, même au niveau élémentaire. Par exemple, beaucoup d’entre eux ne comprennent pas les concepts, le pourquoi et le comment des algorithmes qu’ils enseignent. Ce n’est pas leur faute – le problème remonte à ce qu’on leur a enseigné dans la formation des enseignants et dans leur propre scolarité.

Même le document des normes lui-même est quelque peu difficile à suivre par endroits. Le lire demande une certaine réflexion. J’aimerais que quelqu’un produise un livret qui explique les normes dans un langage simple et avec de nombreux exemples.

Mauvais exemples de « common core » ou de « nouvelles maths »

Exemple 1

Récemment, j’ai vu une image de stratégies de soustraction sur Facebook qui prétendait qu’elle provenait d’un livre de mathématiques de 1ère année et qu’il s’agissait de « maths common core. »

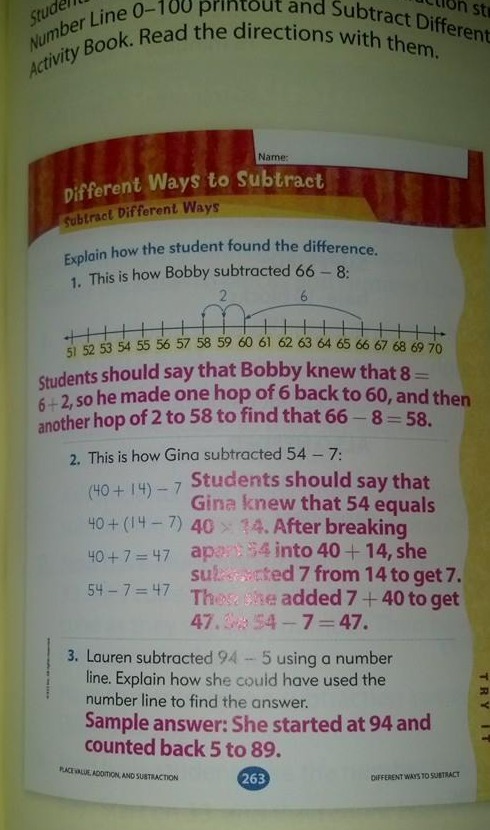
Je pense que la méthode 2 est beaucoup trop difficile pour la 1ère année, et je laisserais même la méthode 1 pour la 2ème année.

Cependant, ce livre ne semble même pas s’aligner sur les normes du Common Core. Les normes pour la 1ère année n’incluent tout simplement pas ce genre de problèmes de soustraction !

C’est ce que nous trouvons dans les normes :

Ajouter et soustraire dans les 20.
1.OA.5.
Relier le comptage à l’addition et à la soustraction (par exemple, en comptant sur 2 pour ajouter 2).
1.OA.6.
Ajouter et soustraire dans les 20, en démontrant de la fluidité pour l’addition et la soustraction dans les 10. Utiliser des stratégies telles que compter, faire des dizaines (p. ex., 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14), décomposer un nombre menant à une dizaine (p. ex., 13 – 4 = 13 – 3 – 1 = 10 – 1 = 9), utiliser la relation entre l’addition et la soustraction (p. ex., sachant que 8 + 4 = 12, on sait que 12 – 8 = 4) et créer des sommes équivalentes mais plus faciles ou connues (p. ex, ajouter 6 +7 en créant l’équivalent connu 6 + 6 + 1 = 12 + 1 = 13).

L’exemple du manuel semble vouloir aborder 1.OA.6 ci-dessus, mais c’est clairement pour l’addition et la soustraction dans la limite de 20, pas avec des nombres plus grands.

Plus tard dans les normes de la 1ère année, nous voyons deux normes qui ont à voir avec la soustraction de nombres à deux chiffres (dans la limite de 100) :

1.NBT.5.
Donné un nombre à deux chiffres, trouver mentalement 10 de plus ou 10 de moins que le nombre, sans avoir à compter ; expliquer le raisonnement utilisé.
1.NBT.6.
Soustraire des multiples de 10 dans l’intervalle 10-90 de multiples de 10 dans l’intervalle 10-90 (différences positives ou nulles), en utilisant des modèles concrets ou des dessins et des stratégies basées sur la valeur de place, les propriétés des opérations, et/ou la relation entre l’addition et la soustraction ; relier la stratégie à une méthode écrite et expliquer le raisonnement utilisé.
Note de Maria : il s’agit de soustractions telles que 34 – 20 ou 89 – 60.

mais ni l’un ni l’autre ne comprend des soustractions comme 54 – 7 ou 82 – 6. Celles-ci sont en 2ème année :

2.NBT.5
Ajouter et soustraire avec aisance dans un intervalle de 100 en utilisant des stratégies basées sur la valeur de place, les propriétés des opérations et/ou la relation entre l’addition et la soustraction.

Notez que la norme de 2e année ne précise pas COMMENT vous soustrayez (si vous utilisez des stratégies de calcul mental ou si vous écrivez des nombres les uns sous les autres et empruntez/regroupez).

Exemple 2

D’après Houghton Mifflin, supposément :

Juanita veut donner des sacs d’autocollants à ses amis. Elle veut donner le même nombre d’autocollants à chaque ami. Elle ne sait pas si elle a besoin de 4 sacs ou de 6 sacs d’autocollants. Combien d’autocollants pourrait-elle acheter pour qu’il n’y ait plus d’autocollants ?

Le problème des autocollants est lié au concept du plus petit commun multiple (LCM). (La réponse est qu’elle devrait acheter 12, 24, 36 ou tout autre multiple de 12 autocollants, car elle peut alors les diviser soit en 4 sacs, soit en 6 sacs.)

Certainement, le problème est TRÈS peu clair et mal formulé. Ma supposition est que le livret dans lequel cela apparaît est simplement non édité. Ce n’est pas la faute des normes elles-mêmes. Je suis d’accord avec Bart Goddard sur Math Forum. C’est un symptôme de la ruée aveugle pour produire des problèmes d’histoires « réelles » qui finissent par être insensés.

D’après le document PDF dans lequel il apparaît, je conclus que le problème est pour la quatrième année, parce que tous les autres problèmes de mots dans le livret correspondent aux normes pour la quatrième année (facteurs, nombres premiers). Mais, les CCS n’incluent même pas le multiple le moins commun dans les normes de 4ème année (c’est en 6ème) ! !! Quelque chose s’est vraiment détraqué avec ce problème de mot.

Exemple 3

A nouveau, censé provenir de Houghton Mifflin pour la 1ère année. Cela correspond à la norme que j’ai déjà citée plus haut :

Ajouter et soustraire dans la limite de 20.
1.OA.6.
Ajouter et soustraire dans la limite de 20, en démontrant une fluidité pour l’addition et la soustraction dans la limite de 10. Utiliser des stratégies telles que compter, faire des dizaines (p. ex., 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14), décomposer un nombre menant à une dizaine (p. ex., 13 – 4 = 13 – 3 – 1 = 10 – 1 = 9), utiliser la relation entre l’addition et la soustraction (p. ex, sachant que 8 + 4 = 12, on sait que 12 – 8= 4) ; et créer des sommes équivalentes mais plus faciles ou connues (par exemple, ajouter 6 +7 en créant l’équivalent connu 6 + 6 + 1 = 12 + 1 = 13).

Bien, tout d’abord, la stratégie consistant à  » faire dix  » a trait à l’ADDITION, et non à la soustraction. En soustraction, on appelle cela « décomposer un nombre menant à une dizaine ». Les instructions devraient donc dire : « Quel est le moyen de décomposer un nombre menant à une dizaine ? ». Je pense que c’est une absurdité totale d’exiger que les élèves de 1ère année connaissent une telle terminologie.

Mais il y a un autre problème ici. Si vous lisez réellement toutes les normes, vous remarquerez qu’à plusieurs autres endroits, il est demandé aux élèves d’expliquer le raisonnement utilisé ou de relier une certaine méthode visuelle à la stratégie, mais PAS dans cette norme !

La façon dont je vois cette norme est que les enseignants sont censés ENSEIGNER les différentes tratégies mentionnées et ensuite donner aux élèves des problèmes SIMPLES d’addition et de soustraction dans les 20, comme 15 – 8 et 10 – 6. Je ne vois PAS cette norme demander aux élèves de reconnaître si un certain modèle visuel correspond à une certaine stratégie.

Encore, il semble que l’auteur jette le bon sens… et ne comprend pas réellement les normes.

Exemple 4

L’exemple ci-dessous est très mal formulé mais le CONCEPT derrière est très bon et se trouve également dans Math Mammoth. Je peux donc comprendre ce qu’ils veulent.

Vous voyez cinq carrés. Coloriez certains en bleu et les autres en rouge. C’est clair.

Coloriez ensuite les carrés de la « liaison numérique » de la même façon. Le lien numérique va à ces trois cercles. Un enfant qui a assisté à une leçon où l’enseignant enseigne les liaisons numériques sait, je l’espère, ce que cela signifie. C’est le même concept qu’une famille de faits… le chiffre du haut est la somme ou le total (5), et les chiffres qui vont aux cercles du bas correspondent à combien vous avez colorié en bleu et combien en rouge, dans ce cas 1 et 4.

Alors je pense que les partenaires cachés sont aussi les 1 et 4. Montrez 1 et 4 doigts à un adulte. Enfin coloriez les 1 et 4 doigts sur l’image (et non vos propres doigts comme cela semble être le cas).

À mon avis, la partie sur les doigts est superflue et confuse. Cependant, le concept des liaisons de nombres est bien plus ancien que le CCS. Les liaisons de nombres ne sont en fait pas mentionnées dans le CCS, bien qu’elles soient liées à cette norme :

1.OA.4
Comprendre la soustraction comme un problème d’addition inconnu. Par exemple,soustraire 10 – 8 en trouvant le nombre qui fait 10 lorsqu’il est ajouté à 8.

et avec celui-ci

1.OA.6.
Ajouter et soustraire dans un intervalle de 20, en démontrant la fluidité pour l’addition et la soustraction dans un intervalle de 10.

Je ne sais pas pourquoi cette feuille de travail sur les obligations numériques est donnée comme un exemple de Common Core Math. Il serait beaucoup mieux intitulé comme un exemple de feuille de travail de mathématiques mal formulée qui POURRAIT même dater d’avant le Common Core (et qui est juste réutilisée dans ce programme d’études particulier)… parce que, comme je l’ai dit, les obligations numériques ne sont PAS mentionnées dans le CCS.

Ce que les normes de mathématiques du Common Core ne sont pas

1. Ils ne sont pas de « nouvelles mathématiques ». Par rapport à de nombreux programmes de mathématiques utilisés dans les années 2000 qui mettaient l’accent sur des algorithmes non traditionnels, le CCS est un mouvement clair vers les algorithmes traditionnels et la mémorisation. Jetez un coup d’œil à ces normes spécifiques :
   

   2.OA.2
   Ajouter et soustraire avec aisance dans la limite de 20 en utilisant des stratégies mentales. À la fin de la 2e année, connaître de mémoire toutes les sommes de deux nombres à un chiffre.
   Note de Maria : ce sont vos faits d’addition de base, comme 7 + 7 ou 5 + 4.

   3.OA.7
   Multiplier et diviser avec aisance dans un intervalle de 100, en utilisant des stratégies telles que la relation entre la multiplication et la division (par exemple, sachant que 8 × 5 = 40, on sait que 40 ÷ 5 = 8) ou les propriétés des opérations. À la fin de la 3e année, connaître de mémoire tous les produits de deux nombres à un chiffre.
   Note de Maria : cela signifie les tables de multiplication et les faits de division de base.

   4.NBT.4
   Ajouter et soustraire avec aisance des nombres entiers à plusieurs chiffres en utilisant l’algorithme standard.

   5.NBT.5
   Multiplier avec aisance des nombres entiers à plusieurs chiffres en utilisant l’algorithme standard.
   Note de Maria : cela ne signifie pas que les élèves multiplient des nombres entiers à plusieurs chiffres seulement en 5e année ; cela est étudié aussi en 3e et 4e années.

2. Les normes n’imposent pas de stratégies étranges ou de modèles visuels aux enseignants et aux élèves. De nombreuses normes laissent le choix aux enseignants et aux élèves. Par exemple :
   

   2.NBT.5
   Ajouter et soustraire avec aisance dans un intervalle de 100 en utilisant des stratégies basées sur la valeur de place, les propriétés des opérations et/ou la relation entre l’addition et la soustraction.

   Notez le « et/ou » dans la phrase ci-dessus. Cela signifie que les enseignants et les élèves ne sont PAS limités à l’utilisation de stratégies spécifiques et qu’on ne leur dit pas d’utiliser plusieurs stratégies. L’algorithme traditionnel de  » l’emprunt  » est une stratégie basée sur la valeur de place, elle est donc incluse ici même dans 2.NBT.5.

   2.NBT.9
   Expliquer pourquoi les stratégies d’addition et de soustraction fonctionnent, en utilisant la valeur de place et les propriétés des opérations. Les explications peuvent être appuyées par des dessins ou des objets.

   Il est dit « peut être appuyé par des dessins » mais cela ne vous oblige pas à le faire, ni ne vous limite à utiliser un modèle visuel ou un type de dessin spécifique.

   3.OA.3
   Utiliser la multiplication et la division à l’intérieur de 100 pour résoudre des problèmes de mots dans des situations impliquant des groupes égaux, des tableaux et des quantités mesurées,par exemple, en utilisant des dessins et des équations avec un symbole pour le nombre inconnu pour représenter le problème.

   L’élève n’est pas obligé d’utiliser un dessin. Cela est juste mentionné comme une possibilité.

   4.NBT.5
   Multiplier un nombre entier d’au plus quatre chiffres par un nombre entier d’un chiffre, et multiplier deux nombres de deux chiffres, en utilisant des stratégies basées sur la valeur de place et les propriétés des opérations. Illustrer et expliquer le calcul à l’aide d’équations, de tableaux rectangulaires et/ou de modèles aréolaires.

   Notez le « et/ou ». Illustrez le calcul mais il est suffisant de l’illustrer en utilisant des équations. Vous n’êtes pas obligé de l’illustrer en utilisant des tableaux.

   Cela dit, certaines normes mentionnent un modèle visuel spécifique, comme une ligne de nombres ou un modèle d’aire rectangulaire, mais c’est moins courant que de donner un choix comme dans les normes ci-dessus.

Mathématiques conceptuelles

Il y a certaines normes qui entrent dans le côté conceptuel des mathématiques que les enseignants de l’école élémentaire peuvent ne pas comprendre si on ne leur enseigne pas ce qu’elles signifient ; par exemple :

5. NF.7b
Interpréter la division d’un nombre entier par une fraction unitaire, et calculer de tels quotients. Par exemple, créer un contexte d’histoire pour 4 ÷ (1/5), et utiliser un modèle visuel de fraction pour montrer le quotient. Utilisez la relation entre la multiplication et la division pour expliquer que 4 ÷ (1/5) = 20 parce que 20 × (1/5) = 4.

Un tel problème d’histoire serait : combien de morceaux de 1/5 pied de long pouvez-vous couper dans un morceau de matériau de 4 pieds ? Un modèle visuel pourrait montrer 4 entiers, divisés en cinquièmes. On peut alors compter que 4 entiers ont un total de 20 cinquièmes.

5.NF.4b
Trouver l’aire d’un rectangle avec des longueurs de côté fractionnaires en le carrelant avec des carrés unitaires des longueurs de côté fractionnaires appropriées, et montrer que l’aire est la même que celle qui serait trouvée en multipliant les longueurs de côté. Multiplier les longueurs latérales fractionnaires pour trouver les aires des rectangles, et représenter les produits fractionnaires comme des aires rectangulaires.

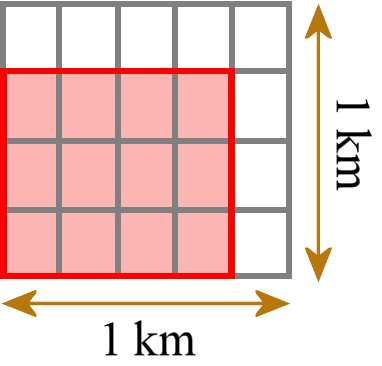C’est-à-dire par exemple un rectangle avec des longueurs latérales de 3/4 km et 4/5 km. Ensuite, nous le carrelons avec des petits rectangles unitaires (et non des carrés unitaires ; ici, la norme elle-même a la mauvaise terminologie) qui ont chacun des longueurs de côté 1/4 km et 1/5 km.

Nous pouvons compter combien de petits carreaux nous avons besoin. Nous avons besoin de 12 de ces tuiles. Chaque tuile a une superficie de 1/20 km2, donc la superficie totale est de 12/20 km2. Ensuite, nous vérifions et comparons que nous obtenons la même réponse que si nous avions multiplié les deux longueurs de côté en utilisant la multiplication régulière des fractions (3/4 km × 4/5 km = 12/20 km2).

J’ai toujours eu ce genre de problèmes dans mes livres – même avant l’arrivée de CCS.

Certains prétendent que les enfants n’ont pas besoin d’une telle compréhension conceptuelle ou que c’est trop difficile. Personnellement, je ne suis pas d’accord. Je me suis toujours efforcé (également avant le CCS) d’expliquer les concepts de l’arithmétique des fractions afin que les élèves ne finissent pas par « suivre aveuglément les règles », uniquement capables de calculer avec des fractions s’il leur arrive de se souvenir correctement de la règle. J’ai toujours mis l’accent sur la compréhension conceptuelle en mathématiques (comme mes lecteurs le savent !).

Mais, j’espère que vous pouvez voir comment certaines de ces choses peuvent être peu familières aux enseignants et aux parents de l’école, et il n’est donc pas étonnant que suivre les normes du Common Core soit difficile pour eux.

C’est mon espoir que Math Mammoth Light Blue Series et les unités que je vends à mes magasins Teachers Pay Teachers et Teachers’ Notebook peuvent aider ces enseignants &parents qui ont besoin de matériel aligné sur le Common Core. Et comme je l’ai dit, le reste d’entre vous peut être confiant en les utilisant aussi. Ils ne contiennent pas de mathématiques « étranges » ou absurdes, mais comme toujours, ils sont simplement basés sur la base solide de l’enseignement des concepts de mathématiques en même temps que les procédures.

Par Maria Miller