L’identité d’Euler semble déroutante :

Elle émerge d’une formule plus générale :

Yowza — nous relions un exposant imaginaire au sinus et au cosinus ! Et d’une certaine manière, en branchant pi, on obtient -1 ? Est-ce que cela pourrait jamais être intuitif ?

Pas selon le mathématicien des années 1800 Benjamin Peirce :

C’est absolument paradoxal ; nous ne pouvons pas le comprendre, et nous ne savons pas ce que cela signifie, mais nous l’avons prouvé, et donc nous savons que cela doit être la vérité.

Argh, cette attitude me fait bouillir le sang ! Les formules ne sont pas des sortilèges à mémoriser : il faut, il faut, il faut trouver une intuition. Voici la mienne :

La formule d’Euler décrit deux façons équivalentes de se déplacer dans un cercle.

C’est tout ? Cette étonnante équation concerne le fait de tourner sur soi-même ? Oui — et nous pouvons la comprendre en nous appuyant sur quelques analogies :

• En partant du nombre 1, voyez la multiplication comme une transformation qui change le nombre : $1 \cdot e^{i \pi}$
• La croissance exponentielle régulière augmente continuellement 1 par un certain taux pendant une certaine période de temps ; la croissance exponentielle imaginaire fait continuellement tourner 1 pendant une certaine période de temps
• Croître pour des unités de temps « pi » signifie faire pi radians autour d’un cercle
• Donc, $e^{i \pi}$ signifie commencer à 1 et faire tourner pi (la moitié d’un cercle) pour arriver à -1

C’est la vue de haut niveau, plongeons dans les détails. Au fait, si quelqu’un essaie de vous impressionner avec $e^{i \pi} = -1$, demandez-lui ce qu’est i à la i-ième puissance. S’ils ne peuvent pas y réfléchir, la formule d’Euler est encore une formule magique pour eux.

Mise à jour : En écrivant, j’ai pensé qu’une vidéo pourrait aider à expliquer les idées plus clairement :

Comprendre cos(x) + i * sin(x)

Le signe égal est surchargé. Parfois nous voulons dire « mettre une chose à une autre » (comme x = 3) et d’autres fois nous voulons dire « ces deux choses décrivent le même concept » (comme $\sqrt{-1} = i$).

La formule d’Euler est cette dernière : elle donne deux formules qui expliquent comment se déplacer dans un cercle. Si nous examinons le mouvement circulaire en utilisant la trigonométrie, et que nous parcourons x radians :

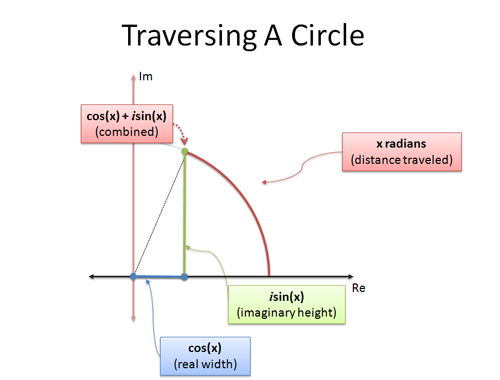
• cos(x) est la coordonnée x (distance horizontale)
• sin(x) est la coordonnée y (distance verticale)

L’énoncé

est une façon astucieuse de condenser les coordonnées x et y en un seul nombre. L’analogie « les nombres complexes sont bidimensionnels » nous aide à interpréter un seul nombre complexe comme une position sur un cercle.

Lorsque nous fixons x à $\pi$, nous nous déplaçons de $\pi$ unités le long de l’extérieur du cercle unitaire. Comme la circonférence totale est de $2\pi$, le bon vieux $\pi$ est à mi-chemin, ce qui nous place à -1.

Neato : Le côté droit de la formule d’Euler ($\cos(x) + i \sin(x)$) décrit le mouvement circulaire avec des nombres imaginaires. Maintenant, découvrons comment le côté e de l’équation l’accomplit.

Qu’est-ce qu’une croissance imaginaire ?

Combiner les coordonnées x et y en un nombre complexe est délicat, mais gérable. Mais que signifie un exposant imaginaire ?

Reculons un peu. Quand je vois $3^4$, je pense à cela comme ceci:

• 3 est le résultat final de la croissance instantanée (en utilisant e) à un taux de ln(3). En d’autres termes : $3 = e^{\ln(3)}$
• $3^4$ est la même chose que de croître jusqu’à 3, mais ensuite de croître pendant 4x plus longtemps. Donc $3^4 = e^{\ln(3) \cdot 4} = 81$

Au lieu de voir les nombres en eux-mêmes, vous pouvez les considérer comme quelque chose vers lequel e a dû « grandir ». Les nombres réels, comme 3, donnent un taux d’intérêt de ln(3) = 1,1, et c’est ce que e « recueille » au fur et à mesure qu’il avance, en croissant continuellement.

La croissance régulière est simple : elle continue à « pousser » un nombre dans la même direction, réelle, qu’il suivait. 3 × 3 pousse dans la direction initiale, la rendant 3 fois plus grande (9).

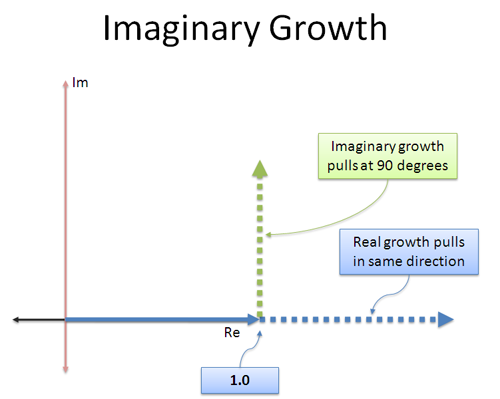
La croissance imaginaire est différente : les « intérêts » que nous gagnons sont dans une direction différente ! C’est comme un moteur à réaction qui a été attaché sur le côté — au lieu d’aller vers l’avant, nous commençons à pousser à 90 degrés.

La chose astucieuse à propos d’une poussée orthogonale (perpendiculaire) constante est qu’elle ne vous accélère pas ou ne vous ralentit pas — elle vous fait tourner ! Prendre n’importe quel nombre et le multiplier par i ne changera pas sa magnitude, juste la direction qu’il pointe.

Intuitivement, voici comment je vois le taux de croissance imaginaire continu : « Quand je grandis, ne me pousse pas en avant ou en arrière dans la direction où je vais déjà. Faites-moi tourner à la place. »

Mais ne devrions-nous pas tourner de plus en plus vite?

Je me suis aussi posé cette question. La croissance régulière se compose dans notre direction initiale, donc nous allons 1, 2, 4, 8, 16, multipliant 2x à chaque fois et restant dans les nombres réels. Nous pouvons considérer cela $e^{\ln(2)x}$, ce qui signifie croître instantanément à un taux de ln(2) pendant « x » secondes.

Et hé — si notre taux de croissance était deux fois plus rapide, 2ln(2) vs ln(2), cela ressemblerait à croître pendant deux fois plus longtemps (2x vs x). La magie de e nous permet de permuter le taux et le temps ; 2 secondes à ln(2) est la même croissance que 1 seconde à 2ln(2).

Maintenant, imaginez que nous avons un certain taux de croissance purement imaginaire (Ri) qui nous fait tourner jusqu’à ce que nous atteignions i, ou 90 degrés vers le haut. Que se passe-t-il si nous doublons ce taux à 2Ri, allons-nous sortir du cercle ?

Nope ! Avoir un taux de 2Ri signifie que nous tournons simplement deux fois plus vite, ou alternativement, tourner à un taux de R pendant deux fois plus longtemps, mais nous restons sur le cercle. Tourner deux fois plus longtemps signifie que nous sommes maintenant orientés à 180 degrés.

Une fois que nous réalisons qu’un certain taux de croissance exponentielle peut nous faire passer de 1 à i, augmenter ce taux ne fait que nous faire tourner davantage. Nous n’échapperons jamais au cercle.

Cependant, si notre taux de croissance est complexe (a+bi vs Ri), alors la partie réelle (a) nous fera croître normalement, tandis que la partie imaginaire (bi) nous fait tourner. Mais ne soyons pas trop fantaisistes : La formule d’Euler, $e^{ix}$, concerne la croissance purement imaginaire qui nous maintient sur le cercle (plus loin).

Un rapide contrôle de sanité

Pendant l’écriture, j’ai dû clarifier quelques questions pour moi-même :

Pourquoi utiliser $e^x$, ne sommes-nous pas en train de faire tourner le nombre 1 ?

e représente le processus de commencer à 1 et de croître continuellement à 100% d’intérêt pour 1 unité de temps.

Quand nous écrivons e, nous capturons tout ce processus dans un seul nombre — e représente tout le charabia de la croissance continue. Donc, en réalité, $e^x$ dit « commencer à 1 et croître continuellement à 100% pendant x secondes », et commence à 1 comme nous le voulons.

Mais que fait i en tant qu’exposant ?

Pour un exposant régulier comme $3^4$, nous demandons :

• Quel est le taux de croissance implicite ? On croît de 1 à 3 (la base de l’exposant).
• Comment change-t-on ce taux de croissance ? Nous le mettons à l’échelle par 4x (la puissance de l’exposant).

Nous pouvons convertir notre croissance au format « e » : notre taux instantané est ln(3), et nous l’augmentons à ln(3) * 4. Encore une fois, la puissance de l’exposant (4) vient de mettre à l’échelle notre taux de croissance.

Lorsque l’exposant supérieur est i (comme dans $3^i$), nous multiplions simplement notre taux de croissance implicite par i. Ainsi, au lieu de croître au bon vieux ln(3), nous croissons au ln(3) * i.

La partie supérieure de l’exposant modifie le taux de croissance implicite de la partie inférieure.

The Nitty Gritty Details

Regardons cela de plus près. Rappelez-vous cette définition de e:

Ce $\frac{100\%}{n}$ représente la portion d’intérêt que nous avons gagné dans chaque période microscopique. Nous avons supposé que le taux d’intérêt était de 100% dans la dimension réelle — mais que se passerait-il s’il était de 100% dans la direction imaginaire ?

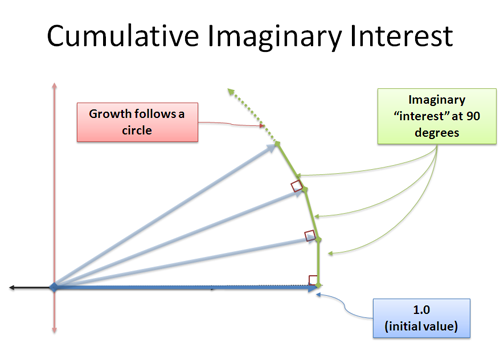
Maintenant, notre intérêt nouvellement formé s’ajoute à nous dans la direction à 90 degrés. Étonnamment, cela ne change pas notre longueur — c’est un concept délicat, car il semble faire un triangle où l’hypoténuse doit être plus grande. Nous avons affaire à une limite, et la distance supplémentaire se situe dans la marge d’erreur que nous spécifions. C’est un sujet que je veux aborder un autre jour, mais prenez ma parole : la croissance perpendiculaire continue vous fera tourner. C’est le cœur du sinus et du cosinus, où votre changement est perpendiculaire à votre position actuelle, et vous vous déplacez dans un cercle.

Nous appliquons i unités de croissance par incréments infiniment petits, chacun nous poussant à un angle de 90 degrés. Il n’y a pas de rotation  » de plus en plus rapide  » – au lieu de cela, nous rampons le long du périmètre sur une distance de |i| = 1 (magnitude de i).

Et hé — la distance rampée autour d’un cercle est un angle en radians ! Nous avons trouvé une autre façon de décrire le mouvement circulaire !

Pour obtenir un mouvement circulaire : Changer continuellement en tournant à un angle de 90 degrés (aka taux de croissance imaginaire).

Donc, la formule d’Euler dit « la croissance exponentielle, imaginaire trace un cercle ». Et ce chemin est le même que se déplacer dans un cercle en utilisant le sinus et le cosinus dans le plan imaginaire.

Dans ce cas, le mot « exponentiel » prête à confusion parce que nous voyageons autour du cercle à un taux constant. Dans la plupart des discussions, on suppose que la croissance exponentielle a un effet cumulatif, composé.

Quelques exemples

Vous ne me croyez pas vraiment, n’est-ce pas ? Voici quelques exemples, et comment y penser intuitivement.

Exemple : $e^i$

Où est le x ? Ah, c’est juste 1. Intuitivement, sans sortir une calculatrice, on sait que cela signifie « parcourir 1 radian le long du cercle unité ». Dans ma tête, je vois « e » essayant de croître de 1 à 100% tous dans la même direction, mais i continue de déplacer la balle et force « 1 » à croître le long du bord d’un cercle:

Pas le plus joli des nombres, mais il est là. N’oubliez pas de mettre votre calculatrice en mode radian lorsque vous le poinçonnez.

Exemple : $3^i$

Ceci est délicat — ce n’est pas dans notre format standard. Mais souvenez-vous,

Nous voulons une croissance initiale de 3x à la fin de la période, ou un taux instantané de ln(3). Mais, le i arrive et change ce taux de ln(3) en « i * ln(3) »:

Nous pensions que nous allions nous transformer à un taux régulier de ln(3), un peu plus rapide que 100% de croissance continue puisque e est environ 2,718. Mais oh non, i nous a fait tourner : maintenant nous nous transformons à un taux imaginaire ce qui signifie que nous ne faisons que tourner autour. Si i était un nombre régulier comme 4, il nous aurait fait croître 4 fois plus vite. Maintenant, nous grandissons à une vitesse de ln(3), mais latéralement.

Nous devrions nous attendre à un nombre complexe sur le cercle unitaire — il n’y a rien dans le taux de croissance pour augmenter notre taille. Résoudre l’équation :

Donc, plutôt que de finir à « 1 » unité autour du cercle (comme $e^i$), nous finissons à ln(3) unités autour.

Exemple : $i^i$

Il y a quelques mois, cela m’aurait fait pleurer. Pas aujourd’hui ! Décomposons les transformations :

Nous commençons par 1 et voulons le modifier. Comme résoudre $3^i$, quel est le taux de croissance instantané représenté par i comme base?

Hrm. Normalement, nous ferions ln(x) pour obtenir le taux de croissance nécessaire pour atteindre x à la fin de 1 unité de temps. Mais pour un taux imaginaire ? Nous devons nous pencher sur la question.

Pour commencer avec 1 et croître jusqu’à i, nous devons commencer à tourner dès le départ. A quelle vitesse ? Eh bien, nous devons obtenir 90 degrés (pi/2 radians) en 1 unité de temps. Notre vitesse est donc de $i \frac{\pi}{2}$. N’oubliez pas que notre vitesse doit être imaginaire puisque nous sommes en rotation, et non en croissance ! Le bon vieux $\frac{\pi}{2}$ est d’environ 1,57 et entraîne une croissance régulière.

Cela devrait être logique : pour transformer 1,0 en i à la fin d’une unité, nous devrions faire une rotation de $\frac{\pi}{2}$ radians (90 degrés) dans cette quantité de temps. Donc, pour obtenir « i », nous pouvons utiliser $e^{i \frac{\pi}{2}}$.

Phew. Cela décrit i comme base. Qu’en est-il de l’exposant ?

Eh bien, l’autre i nous dit de changer notre taux — oui, ce taux que nous avons mis si longtemps à déterminer ! Donc plutôt que de tourner à une vitesse de $i \frac{\pi}{2}$, ce que signifie une base de i, nous transformons le taux en:

Les i s’annulent et rendent le taux de croissance à nouveau réel ! Nous avons fait tourner notre taux et nous nous sommes poussés dans les nombres négatifs. Et un taux de croissance négatif signifie que nous nous rétrécissons — nous devrions nous attendre à ce que $i^i$ rende les choses plus petites. Et c’est le cas:

Tada ! (Cherchez « i^i » sur Google pour utiliser sa calculatrice)

Prenez une respiration : Vous pouvez intuitivement comprendre comment les bases imaginaires et les exposants imaginaires devraient se comporter. Whoa.

Et en bonus, vous avez compris ln(i) — pour que $e^x$ devienne i, faites tourner e de $\frac{\pi}{2}$ radians.

Exemple : (i^i)^i

Un double exposant imaginaire ? Si vous insistez. Tout d’abord, nous savons ce que sera notre taux de croissance à l’intérieur de la parenthèse :

Nous obtenons un taux de croissance négatif (décroissant) de -pi/2. Et maintenant nous modifions à nouveau ce taux par i:

Et maintenant nous avons une rotation négative ! Nous faisons le tour du cercle à un taux de $-\frac{\pi}{2}$ par unité de temps. Combien de temps allons-nous faire ? Eh bien, il y a une unité de temps implicite « 1 » tout en haut de cette chaîne d’exposants ; la valeur implicite par défaut est d’aller jusqu’à 1 unité de temps (tout comme $e = e^1$). 1 unité de temps nous donne une rotation de $-\frac{\pi}{2}$ radians (-90 degrés) ou -i!

Et, juste pour le plaisir, si nous élevions au carré ce résultat fou:

C’est « juste » deux fois la rotation : 2 est un nombre régulier donc double notre taux de rotation à un plein -180 degrés dans une unité de temps. Ou, vous pouvez le voir comme l’application d’une rotation de -90 degrés deux fois de suite.

À première vue, ce sont des exposants vraiment étranges. Mais avec nos analogies, nous pouvons les prendre dans la foulée.

Croissance complexe

Nous pouvons avoir une croissance réelle et imaginaire en même temps : la partie réelle nous met à l’échelle, et la partie imaginaire nous fait tourner autour :

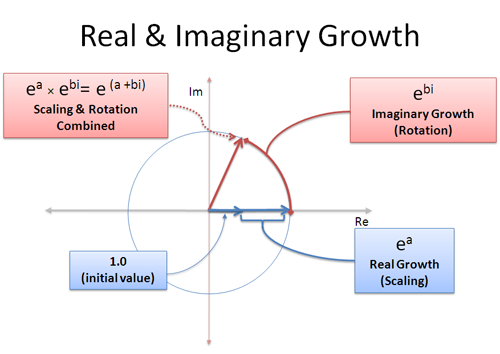
Un taux de croissance complexe comme (a + bi) est un mélange de croissance réelle et imaginaire. La partie réelle a, signifie « croître à 100% pendant a secondes » et la partie imaginaire b signifie « tourner pendant b secondes ». Rappelez-vous, les rotations ne bénéficient pas de l’avantage de la capitalisation puisque vous continuez à  » pousser  » dans une direction différente — la rotation s’additionne linéairement.

Avec cela en tête, nous pouvons représenter n’importe quel point sur n’importe quel cercle de taille en utilisant (a+bi) ! Le rayon est $e^a$ et l’angle est déterminé par $e^{bi}$. C’est comme si vous mettiez le nombre dans l’expanseur-o-tron pendant deux cycles : une fois pour le faire grandir à la bonne taille (a secondes), une autre fois pour le faire tourner au bon angle (b secondes). Ou, vous pourriez d’abord le faire tourner et ensuite le faire croître !

Disons que nous voulons connaître la quantité de croissance pour obtenir 6 + 8i. Cela revient à demander le logarithme naturel d’un nombre imaginaire : comment faire croître e pour obtenir (6 + 8i) ?

• Radius : De quelle taille de cercle avons-nous besoin ? Eh bien, la magnitude est de $\sqrt{6^2 + 8^2} = \sqrt{100} = 10$. Ce qui signifie que nous devons croître pendant ln(10) = 2,3 secondes pour atteindre cette quantité.
• Montant à tourner : Quel est l’angle de ce point ? Nous pouvons utiliser arctan pour le déterminer : atan(8/6) = 53 degrés = .93 radian.
• Combinaison du résultat : ln(6+8i) = 2,3 + .93i

C’est-à-dire que nous pouvons atteindre le point aléatoire (6 + 8i) si nous utilisons $e^{2.3 + .93i}$.

Pourquoi est-ce utile ?

La formule d’Euler nous donne une autre façon de décrire le mouvement dans un cercle. Mais nous pouvions déjà le faire avec le sinus et le cosinus — qu’est-ce qui est si spécial ?

C’est une question de perspective. Le sinus et le cosinus décrivent le mouvement en termes de grille, traçant les coordonnées horizontales et verticales.

La formule d’Euler utilise des coordonnées polaires — quel est votre angle et votre distance ? Encore une fois, il s’agit de deux façons de décrire le mouvement :

• Système de grille : Allez 3 unités à l’est et 4 unités au nord
• Coordonnées polaires : Allez 5 unités à un angle de 53,13 degrés

Selon le problème, les coordonnées polaires ou rectangulaires sont plus utiles. La formule d’Euler nous permet de convertir entre les deux pour utiliser le meilleur outil pour le travail. De plus, comme $e^{ix}$ peut être converti en sinus et cosinus, nous pouvons réécrire les formules de trigonométrie comme des variations de e, ce qui est très pratique (pas besoin de mémoriser sin(a+b), vous pouvez le dériver — plus un autre jour). Et c’est beau que chaque nombre, réel ou complexe, soit une variation de e.

Mais utilité, schmutilité : le résultat le plus important est la réalisation que les équations déroutantes peuvent devenir intuitives avec les bonnes analogies. Ne laissez pas de belles équations comme la formule d’Euler rester un sort magique — construisez sur les analogies que vous connaissez pour voir les perspicacités à l’intérieur de l’équation.

Happy math.

Appendice

La screencast était amusante, et les commentaires sont définitivement les bienvenus. Je pense que cela aide les idées à sauter, et marcher à travers l’article m’a aidé à trouver des lacunes dans mon intuition.

• Brian Slesinsky a une présentation soignée sur la formule d’Euler
• Visual Complex Analysis a une grande discussion sur la formule d’Euler — voir p. 10 dans le Google Book Preview
• J’ai fait un exposé sur les mathématiques et les analogies qui explique l’identité d’Euler plus visuellement :

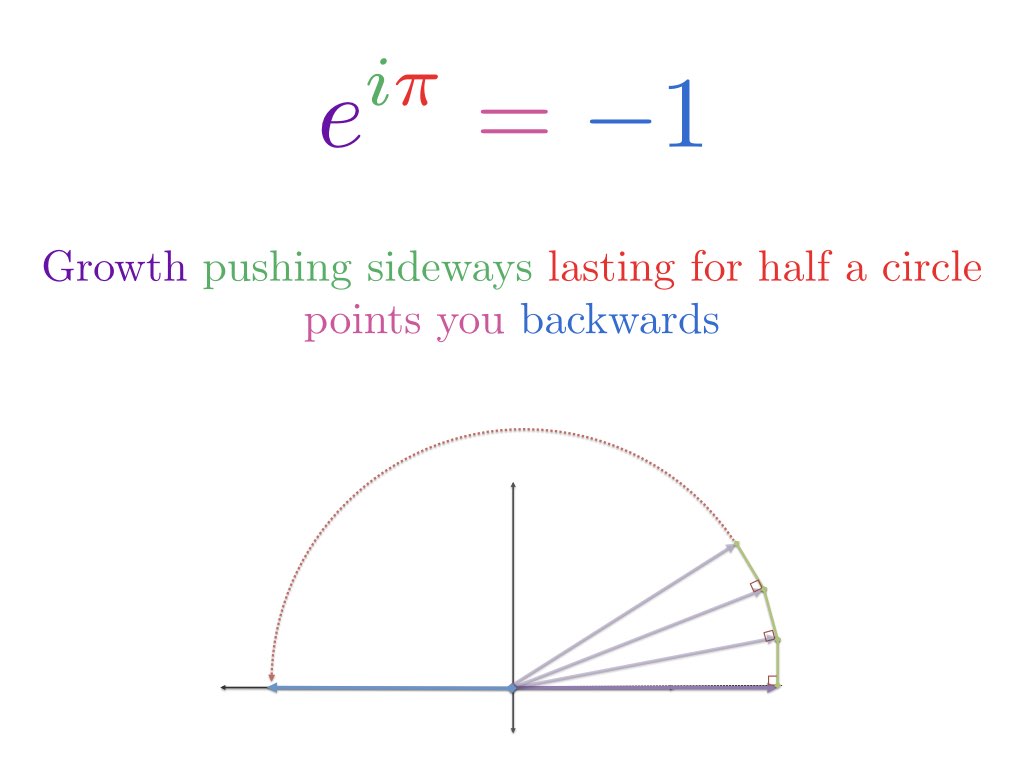
Autres posts dans cette série

1. Un guide visuel et intuitif des nombres imaginaires
2. Arithmétique intuitive avec les nombres complexes
3. Comprendre pourquoi la multiplication complexe fonctionne
4. Guide intuitif des angles, Degrés et Radians
5. Compréhension intuitive de la formule d’Euler
6. Un guide interactif de la transformée de Fourier
7. Guide intuitif de la convolution

.

8. Compréhension intuitive des ondes sinusoïdales
9. Un guide intuitif de l’algèbre linéaire
10. Intuition du programmeur pour la multiplication matricielle
11. Multiplication imaginaire vs. Exposants imaginaires

.