
Galilée est souvent considéré comme le père de la science moderne. C’est lui qui a rassemblé les principes de l’expérience, de la théorie et des mathématiques dans un cadre standard. Probablement plus que quiconque, Galilée est la personne responsable du développement de la science moderne.
On raconte que Galilée a lâché deux billes d’acier de masses différentes, mais du même matériau depuis la tour penchée de Pise et qu’elles ont atterri en même temps. Ce qui est remarquable à propos de cette expérience, c’est qu’il a inauguré une nouvelle méthode de faire de la science où vous conduisez une expérience pour tester une hypothèse. Il a montré que nous devons faire plus que simplement penser que quelque chose est vrai, mais aussi que nous devons le prouver.

Galilée a trouvé un paradoxe intéressant alors qu’il était le chef du département de mathématiques de l’université de Pise.
Définition : Un paradoxe, également appelé antinomie, est un énoncé logiquement auto-contradictoire ou un énoncé qui va à l’encontre de l’attente de quelqu’un. (Wikipedia). (Grec : « para » = au-delà, « doxa » = croyance)
Le paradoxe de Galilée consistait à déterminer si deux ensembles contenant des objets infinis sont équivalents entre eux. Par exemple, que P soit l’ensemble des entiers positifs où P= {0,1,2,3,…} et E l’ensemble des nombres pairs où E = {0,2,4,6,…}. Galilée prétendait que les tailles de ces deux ensembles vont être les mêmes parce que nous pouvons apparier chaque entier positif de l’ensemble P avec les nombres pairs de l’ensemble E.

Alors comment la taille des deux ensembles peut-elle être la même lorsqu’un nombre « inférieur » apparaît dans E ? C’est ce qu’on a appelé le paradoxe de Galilée et qui a lancé un nouveau débat sur le concept d’infini.
Après Galilée, son élève Evangelista Torricelli est devenu le chef du département de mathématiques de l’université de Pise. Vous avez peut-être entendu parler de lui en raison de ses travaux sur la pression atmosphérique et de l’invention du baromètre. Comme Toricelli s’intéresse aussi aux mathématiques, il demande :
Est-il possible d’avoir un objet avec un volume fini et une surface infinie ? En premier lieu, une telle chose semble improbable pour la plupart d’entre nous. Cependant, les mathématiques nous disent qu’une telle chose pourrait se produire. Torricelli a répondu lui-même à sa question et a découvert la Trompette de Toricelli dont la surface est infinie, mais le volume fini. Sa découverte vue comme un paradoxe « incroyable ».
A propos, il y a une règle essentielle dans la philosophie des mathématiques ; Quelle que soit l’époque de la philosophie ou des mathématiques à laquelle vous avez affaire, elle est liée à l’histoire, la culture et la religion de cette région. C’est pourquoi on appelle la trompette de Toricelli aussi la corne de Gabriel. Une référence est faite ici à la Bible parce que les chrétiens croient que l’ange, Gabriel, soufflera dans la corne le jour du jugement.
Alors, comment se forme la trompette de Toricelli ? Nous savons tous comment faire un graphique de y=x. Si vous représentez plutôt l’équation y=1/x où x est supérieur ou égal à 1, le graphique sera comme ceci :
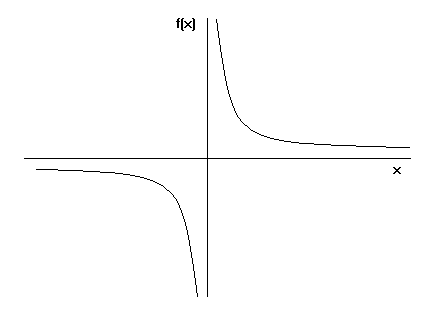
Lorsque nous prenons le graphique de y=1/x et que nous le faisons tourner autour de l’axe des x, nous voyons la trompette de Toricelli.

Heureusement, nous avons entre les mains des formules mathématiques pour calculer l’aire et le volume de la trompette de Toricelli. Lorsque nous utilisons la formule d’intégration ci-dessous pour le volume de la trompette, nous obtenons une quantité finie.
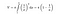
Par contre, lorsque nous appliquons la formule d’intégration pour la surface de la trompette, cette fois, la surface de celle-ci devient infinie. Ce résultat n’est-il pas intéressant ?
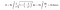
Puisque le volume de la trompette de Toricelli est fini, nous pouvons la remplir avec une quantité finie de peinture. Par exemple, supposons que le volume de la trompette est de 100 litres. Je vais chez Home Depot, j’achète 100 litres de peinture et je la remplis. Cependant, ce qui rend la chose intéressante, c’est que j’aurai peint la surface infinie avec ces 100 litres de peinture. Aujourd’hui, la plupart des gens appellent ce paradoxe, « le paradoxe du peintre. »
Houston, nous avons un problème ici ! La situation qui est impossible en pratique devient possible en mathématiques. Alors, comment la trompette de Torricelli peut-elle être réelle ? Ou encore, comment pouvons-nous faire correspondre précisément tous les éléments des ensembles alors qu’un des ensembles est un sous-ensemble d’un autre dans l’exemple de Galilée ?
La raison de tous ces conflits est que le concept d’infini n’est pas similaire aux autres concepts que nous connaissons, et cela déroute beaucoup de gens. Galilée dit pour son paradoxe,
« Oui, mon ami, l’infini existe. Il est futile de s’y opposer. Les ensembles sur lesquels je travaille sont des exemples d’ensembles fermés qui impliquent l’infini. Ils commencent à un point et vont jusqu’à l’infini, et pourtant, ils sont toujours des ensembles. Cependant, mes commentaires et mes concepts concernant l’infini doivent être différents de ceux que j’utiliserais pour des magnitudes finies. Si vous avez affaire à des magnitudes finies, vous pouvez dire que 3 kilos sont inférieurs à 5 kilos, ou que 32 mètres sont plus longs que 7 mètres. Mais quand il s’agit d’infini, vous ne pouvez pas dire que cet infini est plus grand, plus petit ou égal à cela. »
C’était la solution de Galilée 1600s.
Malheureusement, la solution de Galilée avait commencé un nouveau débat sur l’infini. Les mathématiciens et les philosophes ne pouvaient pas se mettre d’accord sur une réponse spécifique jusqu’à ce que Cantor partage sa « théorie des ensembles », que les étudiants apprennent à l’école primaire aujourd’hui.
Nous pouvons périodiquement historiciser le développement de l’idée de l’infini. Elle a d’abord émergé des Éléates, qui était une école de philosophie présocratique fondée par Parménide au début du cinquième siècle avant JC dans la ville antique d’Élée. Cette école comptait trois grands philosophes, tels que Zénon, Xénophane et Parménide. Dans cette école, la philosophie acceptée était que l’existence était singulière, et qu’il n’y avait pas de pluralité. Zénon était célèbre pour ses paradoxes sur l’infini chez les Éléates. Plus tard, dans les années 300 avant Jésus-Christ, Aristoteles a surgi et a proposé une paire de concepts pour expliquer les paradoxes de Zénon, qui étaient l’infini potentiel et l’infini réel.
L’infini potentiel est un groupe de nombres ou un groupe de « choses » qui continue sans se terminer, continuant ou se répétant encore et encore sans point final reconnaissable.
L’infini réel implique des ensembles ou des « choses » sans fin dans un espace qui a un début et une fin ; c’est une série qui est techniquement « complétée » mais qui consiste en un nombre infini de membres.
Aristote croyait qu’il n’y avait pas d’infini réel. Cette idée d’Aristote a dominé le monde de la philosophie jusqu’aux années 1600. Ensuite, des philosophes comme Cusa et Bruno ont affirmé qu’il existe un infini réel, mais que nous ne pouvons pas lui donner un sens. Après Cusa et Bruno, le grand penseur Spinoza s’est joint au sujet.
Spinoza a dit que nous pouvions comprendre le concept d’infini et les classer en taille. Cependant, il a également déclaré qu’il ne pouvait pas faire le calcul sur eux. Par exemple, il pouvait ajouter 3 à 5, mais il ne pouvait pas ajouter un infini à un autre.
Finalement, pour terminer ces débats, un bel homme, Georg Cantor s’est présenté et a trouvé la théorie des ensembles, qui est toujours la base des mathématiques. Il a fixé le point final des discussions sur l’infini avec sa théorie des ensembles.
Il nous a montré qu’un ensemble infini serait plus grand ou plus petit qu’un autre ensemble infini. De plus, Cantor a affirmé que nous pouvions ajouter et multiplier des ensembles infinis. Jusqu’à cette époque, les humains avaient suivi les idées d’Aristote sur l’infini. Selon Aristote, si nous multiplions le nombre 3 par l’infini, il redeviendrait infini. L’infini engloutirait tout. Sur cette base, il affirmait qu’il n’y aurait qu’un infini potentiel, et non un infini réel.
Cependant, Cantor nous a prouvé le contraire de l’idée d’Aristote avec la théorie des ensembles. Si on ajoute un à un ensemble infini, ce ne sera plus le même ensemble. Il a essayé de comparer les infinis. Par exemple, Cantor a prouvé que l’ensemble de toutes les fonctions de (0,1)→ℕ est dénombrable. Il a donc défini une fonction biunivoque et onto de l’intervalle (0,1) aux nombres naturels.
En d’autres termes, il a prouvé que tous les nombres naturels peuvent tenir entre 0 et 1 parce qu’il y avait une infinité de nombres rationnels entre 0-1, et que ces infinis peuvent être appariés. Puis il a fait quelque chose d’encore plus dangereux que de trouver deux infinis égaux. Il a comparé l’infinité des nombres réels avec l’infinité des nombres naturels et a trouvé que l’infinité des nombres réels est plus grande que l’autre. Il a même regardé sa preuve et a dit à son ami Dedekind : « Je le vois, mais même moi je ne peux pas le croire… ».
Cantor était aussi un mathématicien avec des préoccupations philosophiques et religieuses très sérieuses. Tout en développant la théorie des ensembles, il a dit : « Dieu m’a dicté la théorie des ensembles ».
La théorie des ensembles n’était pas largement acceptée lorsqu’elle a été développée. Les entreprises n’embauchaient même pas Cantor pour un quelconque emploi. Un mathématicien, Henri Poincaré, a dit un jour : « Les idées de ce Cantor sont une mauvaise maladie qui colle au collet des mathématiques. Et les mathématiques le soigneront un jour ». Cantor a dû aller dans un hôpital psychiatrique pendant un certain temps et y est mort. Mais aujourd’hui, on le considère comme un génie.
Cantor était un homme solitaire au bord de l’infini. Il a cité la Bible au début de son article sur les nombres transfinis : « Tout ce qui est caché sera mis en lumière. »