Imaginez un carré de papier posé à plat sur votre bureau. Je vous demande de fermer les yeux. Vous entendez le papier se déplacer. Lorsque vous ouvrez les yeux, le papier ne semble pas avoir changé. Qu’est-ce que j’aurais pu lui faire pendant que vous ne regardiez pas ?
Il est évident que je n’ai pas fait tourner le papier de 30 degrés, car alors le papier aurait l’air différent.

Je ne l’ai pas non plus retourné à travers une ligne reliant, par exemple, un des coins au milieu d’un autre bord. Le papier aurait été différent si je l’avais fait.

Ce que j’aurais pu faire, cependant, c’est faire tourner le papier dans le sens des aiguilles d’une montre ou dans le sens inverse par un multiple quelconque de 90 degrés, ou le retourner à travers l’une des lignes diagonales ou les lignes horizontales et verticales.
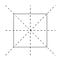
Une façon utile de visualiser les transformations est de marquer les coins du carré.

La dernière option est celle de ne rien faire. C’est ce qu’on appelle la transformation d’identité. Ensemble, elles sont toutes appelées les transformations de symétrie du carré.
Je peux combiner des transformations de symétrie pour en faire d’autres. Par exemple, deux retournements à travers le segment de ligne BD produit l’identité, tout comme quatre rotations successives de 90 degrés dans le sens inverse des aiguilles d’une montre. Un retournement autour de la ligne verticale suivi d’un retournement autour de la ligne horizontale a l’effet sûr d’une rotation de 180 degrés. En général, toute combinaison de transformations de symétrie produira une transformation de symétrie. Le tableau suivant donne les règles de composition des transformations de symétrie:

Dans ce tableau, les R avec les indices 90, 180 et 270 désignent des rotations dans le sens inverse des aiguilles d’une montre de 90, 180 et 270 degrés, H désigne une bascule autour de la ligne horizontale, V une bascule autour de la ligne verticale, MD une bascule autour de la diagonale du haut à gauche au bas à droite, et OD une bascule sur l’autre diagonale. Pour trouver le produit de A et B, allez à la ligne de A et ensuite à la colonne de B. Par exemple, H∘MD=R₉₀.
Il y a plusieurs choses que vous pouvez remarquer en regardant le tableau :
- L’opération ∘ est associative, ce qui signifie que A∘(B∘C) = (A∘B)∘C pour toute transformation A, B et C.
- Pour toute paire de transformations de symétrie A et B, la composition A∘B est aussi une transformation de symétrie
- Il existe un élément e tel que A∘e=e∘A pour toute A
- Pour toute transformation de symétrie A, il existe une unique transformation de symétrie A-¹ telle que A∘A-¹=A-¹∘A=e
On dit donc que la collection des transformations de symétrie d’un carré, combinée à la composition, forme une structure mathématique appelée groupe. Ce groupe est appelé D₄, le groupe dièdre du carré. Ces structures sont le sujet de cet article.
Définition d’un groupe
Un groupe ⟨G,*⟩ est un ensemble G avec une règle * pour combiner deux éléments quelconques dans G qui satisfait les axiomes de groupe:
Dans l’abstrait, nous supprimons souvent * et écrivons a*b comme ab et nous nous référons à * comme une multiplication.

Il n’est pas nécessaire que * soit commutatif, c’est-à-dire que a*b=b*a. On peut s’en rendre compte en regardant la table de D₄, où H∘MD=R₉₀ mais MD∘H=R₂₇₀. Les groupes où * est commutatif sont appelés groupes abéliens d’après Neils Abel.
Les groupes abéliens sont l’exception plutôt que la règle. Un autre exemple de groupe non abélien est celui des transformations de symétrie d’un cube. Considérons seulement les rotations autour des axes :
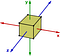
Si je fais d’abord une rotation de 90 degrés dans le sens inverse des aiguilles d’une montre autour de l’axe y, puis de 90 degrés dans le sens inverse des aiguilles d’une montre autour de l’axe z, alors sa aura un résultat différent de celui que j’obtiendrais en faisant une rotation de 90 degrés autour de l’axe z, puis de 90 degrés autour de l’axe y.

Il est possible qu’un élément soit son propre inverse. Considérons le groupe qui est constitué de 0 et de 1 avec l’opération d’addition binaire. Son tableau est:

Il est clair que 1 est son propre inverse. Il s’agit également d’un groupe abélien. Ne vous inquiétez pas, la plupart des groupes ne sont pas aussi ennuyeux.
Plusieurs exemples de groupes incluent :
- L’ensemble des entiers avec addition.
- L’ensemble des nombres rationnels ne comprenant pas 0 avec multiplication.
- L’ensemble des solutions de l’équation polynomiale xⁿ-1=0, appelées les nièmes racines de l’unité, avec multiplication.
Voici quelques exemples qui ne sont pas des groupes :
- L’ensemble des nombres naturels sous addition n’est pas un groupe car il n’y a pas d’inverses, qui seraient les nombres négatifs.
- L’ensemble de tous les nombres rationnels incluant 0 sous multiplication n’est pas un groupe car il n’y a pas de nombre rationnel q pour lequel 0/q=1, donc tout élément n’a pas d’inverse.
Structure de groupe
Un groupe est bien plus qu’un blob qui satisfait les quatre axiomes. Un groupe peut avoir une structure interne, et cette structure peut être très complexe. Un des problèmes de base en algèbre abstraite est de déterminer à quoi ressemble la structure interne d’un groupe, puisque dans le monde réel, les groupes qui sont réellement étudiés sont beaucoup plus grands et plus compliqués que les exemples simples que nous avons donnés ici.
Un des types de base de structure interne est un sous-groupe. Un groupe G a un sous-groupe H lorsque H est un sous-ensemble de G et :
- Pour a,b∈H, a*b∈H et b*a∈H
- Pour a∈H, a-¹∈H
- L’identité est un élément de H
Si H≠G alors H est dit être un sous-groupe propre. Le sous-groupe de G constitué uniquement de l’identité est appelé le sous-groupe trivial.
Un groupe non abélien peut avoir des sous-groupes commutatifs. Considérons le groupe diédral carré dont nous avons parlé dans l’introduction. Ce groupe n’est pas abélien mais le sous-groupe des rotations est abélien et cyclique :
Nous donnons maintenant deux exemples de structure de groupe.
Même si un groupe G n’est pas abélien, il se peut tout de même qu’il existe une collection d’éléments de G qui commute avec tout ce qui est dans G. Cette collection est appelée le centre de G. Le centre C est un sous-groupe de G. Preuve:
Supposons maintenant que f est une fonction dont le domaine et l’étendue sont tous deux G. Une période de f est un élément a∈G tel que f(x)=f(ax) pour tout x∈G. L’ensemble P des périodes de f est un sous-groupe de G. Preuve:
Les groupes finis sont finiment engendrés
On a vu que les groupes cycliques sont engendrés par un seul élément. Lorsqu’il est possible d’écrire chaque élément d’un groupe G comme produits d’un sous-ensemble A (pas nécessairement propre) de G, alors on dit que A engendre G et on écrit cela sous la forme G=⟨A⟩. La preuve la plus « well, duh » que vous verrez jamais est la preuve que tous les groupes finis sont générés par un ensemble générateur fini:
- Let G be finite. Chaque élément de G est un produit de deux autres éléments de G donc G=⟨G⟩. QED.

Nous terminerons cet article par une application.
Communication résistante aux erreurs
La façon la plus simple de transmettre des informations numériques est de les coder dans des chaînes binaires de longueur fixe. Aucun schéma de communication n’est totalement exempt d’interférences, il y a donc toujours une possibilité que les mauvaises données soient reçues. La méthode du décodage à maximum de vraisemblance est une approche simple et efficace pour détecter et corriger les erreurs de transmission.
Disons que 𝔹ⁿ est l’ensemble des chaînes binaires, ou mots, de longueur n. Il est simple de montrer que 𝔹ⁿ est un groupe abélien sous addition binaire sans report (de sorte que par exemple 010+011=001). Notons que tout élément est son propre inverse. Un code C est un sous-ensemble de 𝔹ⁿ. Voici un exemple de code dans 𝔹⁶:
C = {000000, 001011, 010110, 011101, 100101, 101110, 110011, 111000}
Les éléments d’un code sont appelés mots-codes. Seuls les mots de code seront transmis. On dit qu’il y a erreur lorsqu’une interférence modifie un bit dans un mot transmis. La distance d(a,b) entre deux mots-codes a et b est le nombre de chiffres par lesquels deux mots-codes diffèrent. La distance minimale d’un code est la plus petite distance entre deux de ses mots de code. Pour l’exemple de code juste au-dessus, la distance minimale est de trois.
Dans la méthode de décodage à maximum de vraisemblance, si on reçoit un mot x, qui peut contenir des erreurs, le récepteur doit interpréter x comme le mot de code a tel que d(a,x) est un minimum. Je montrerai que pour un code de distance minimale m, cela peut toujours (1) détecter les erreurs qui changent moins de m bits et (2) corriger les erreurs qui changent ½(m-1) ou moins de bits.

Dans notre exemple de code, m=3 et la sphère de rayon ½(m-1)=1 autour du mot code 011101 est {011101, 111101, 001101, 011001, 010101, 011111, 011100}. Donc, si le récepteur reçoit l’un de ces mots, il sait qu’il était censé recevoir 011101.
C’est bien beau tout ça, mais qu’est-ce que tout cela a à voir avec la théorie des groupes ? La réponse se trouve dans la façon dont nous produisons réellement les codes avec lesquels cette méthode fonctionne.
Il est possible pour un code dans 𝔹ⁿ de former un sous-groupe. Dans ce cas, on dit que le code est un code de groupe. Les codes de groupe sont des groupes finis donc ils sont finiment engendrés. Nous allons voir comment produire un code en trouvant un ensemble générateur.
Un code peut être spécifié de telle sorte que les premiers bits de chaque mot de code sont appelés les bits d’information et les bits à la fin sont appelés les bits de parité. Dans notre exemple de code C, les trois premiers bits sont des bits d’information et les trois derniers sont des bits de parité. Les bits de parité satisfont aux équations de contrôle de parité. Pour un mot de code A₁A₂A₃A₄A₅A₆, les équations de parité sont A₄=A₁+A₂, A₅=A₂+A₃, et A₆=A₁+A₃. Les équations de parité fournissent une autre couche de protection contre les erreurs : si l’une des équations de parité n’est pas satisfaite alors une erreur s’est produite.
Voici ce que nous faisons. Supposons que nous voulons des mots de code avec m bits d’information et n bits de parité. Pour générer un code de groupe, écrire une matrice avec m lignes et m+n colonnes. Dans le bloc formé par les m premières colonnes, écrivez la matrice identité m×m. Dans la colonne j pour m+1≤j≤m_n, écrivez un 1 dans la kième ligne si Aₖ apparaît dans l’équation de parité du bit de parité Aⱼ et 0 sinon. Dans notre exemple de code, la matrice est :

Une telle matrice est appelée matrice génératrice du code de groupe. Vous pouvez vérifier directement que les lignes génèrent C:

Les lignes de toute matrice génératrice forment un ensemble générateur pour un code de groupe C. Preuve:
- Identité et inverses : Toute ligne ajoutée à elle-même donne l’identité, une chaîne constituée de tous les zéros.
- Fermeture : Si A,B∈C alors A et B sont des sommes de lignes de la matrice génératrice donc A+B est aussi une somme de lignes de la matrice génératrice. Donc A+B∈C.
Cela nous permet de générer un code, maintenant je vais montrer comment générer un code utile.
Définir le poids w(x) pour signifier le nombre de uns dans x. Par exemple, w(100101)=3. Il est évident que w(x)=d(x,0) où 0 est un mot dont les chiffres sont tous des zéros. Le poids minimum W d’un code est le poids du mot codé non nul ayant le moins de uns dans le code. Pour un code de distance minimale m, d(x,0)≥m donc w(x)≥m et donc W=m.
Rappelons que pour qu’un mot soit considéré comme un mot-code, il doit satisfaire un ensemble d’équations de contrôle de parité. Pour notre exemple de code, celles-ci sont A₄=A₁+A₂, A₅=A₂+A₃, et A₆=A₁+A₃. On peut aussi les écrire sous la forme d’un système linéaire :
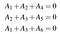
Qui lui-même peut être écrit en termes de produits scalaires :

Ou sous une forme plus compacte comme Ha=0 où a=(A₁,A₂,A₃,A₄,A₅,A₆) et H est la matrice de contrôle de parité pour le code :

On peut vérifier par calcul direct que si w(a)≤2 alors on ne peut pas avoir Ha=0. En général, le poids minimum est t+1 où t est le plus petit nombre tel toute collection de t colonnes de H ne font pas une somme nulle (c’est-à-dire qu’elles sont linéairement indépendantes). Prouver cela nous emmènerait juste un peu trop loin dans l’algèbre linéaire.
Si cela vous effraie, ne vous inquiétez pas. Nous pouvons produire de très bons codes sans cela en profitant du fait que le résultat que je viens de mentionner implique que si chaque colonne de H est non nulle et qu’il n’y a pas deux colonnes égales alors le poids minimum, et donc la distance minimum du code, est au moins de trois. C’est très bien : si notre système de communication est censé avoir une erreur de bit pour cent mots transmis, alors seulement un mot transmis sur dix mille aura une erreur non corrigée et un mot transmis sur un million aura une erreur non détectée.
Nous avons donc maintenant une recette pour produire un code utile pour le schéma de détection à maximum de vraisemblance pour des mots de code contenant m bits d’information et n bits de parité :
- Créer une matrice avec m+n colonnes et n lignes. Remplissez la matrice avec des uns et des zéros de façon à ce qu’il n’y ait pas deux colonnes identiques et qu’aucune colonne ne comporte que des zéros.
- Chaque ligne de la matrice de contrôle de parité résultante correspond à l’une des équations des bits de parité. Ecrivez-les sous forme de système d’équations et résolvez-les de façon à ce que chaque bit de parité s’écrive en fonction des bits d’information.
- Créez une matrice à m+n colonnes et m lignes. Dans le bloc formé par les m premières colonnes, écrire la matrice identité m×m. Dans la colonne j pour m+1≤j≤m_n, écrivez un 1 à la kième ligne si Aₖ apparaît dans l’équation de parité du bit de parité Aⱼ et 0 sinon.
- Les lignes de cette matrice sont les générateurs d’un groupe de code de distance minimale au moins égale à trois. C’est le code que nous utiliserons.
À titre d’exemple, supposons que j’ai besoin d’un code simple de huit mots et que je n’ai besoin que d’une détection d’erreur de base et non d’une correction, donc je peux m’en tirer avec une distance minimale de deux. Je veux trois bits d’information et deux bits de parité. J’écris la matrice de contrôle de parité suivante :
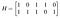
Il y a deux paires de colonnes qui sont égales, donc le plus petit t pour lequel toute collection de t colonnes est linéairement indépendante est un, donc le poids minimum, et donc la distance minimum que j’aurai, est deux. Les lignes représentent les équations de contrôle de parité A₄=A₁+A₃ et A₅=A₁+A₂+A₃. Ma matrice génératrice est donc :

Et les lignes de cette matrice génèrent le groupe de codes :
- {00000, 00111, 01001, 01110, 10011, 10100, 111010, 11101}
Marques finales
L’algèbre abstraite est un sujet profond avec des implications de grande envergure, mais elle est aussi très facile à apprendre. Mis à part quelques mentions passagères d’algèbre linéaire, presque tout ce que j’ai discuté ici est accessible à quelqu’un qui n’a fait que de l’algèbre de lycée.
Lorsque j’ai eu l’idée d’écrire cet article, je voulais vraiment parler du Rubik’s cube, mais finalement j’ai voulu choisir un exemple qui ne pouvait être couvert qu’avec les idées les plus basiques de la théorie des groupes. De plus, il y a tellement de choses à dire sur le groupe du Rubik’s cube qu’il mérite un article autonome, donc cela viendra bientôt.
Mes cours universitaires d’algèbre abstraite étaient basés sur le livre A Book of Abstract Algebra de Charles Pinter, qui est et un traitement accessible. Les exemples dans cet article ont tous été empruntés avec quelques modifications à Pinter.
En guise de note finale, toutes les images qui ne sont pas citées sont mon propre travail original et peuvent être utilisées avec attribution. Comme toujours, j’apprécie toute correction ou demande de clarification.