Les valeurs propres sont un ensemble spécial de scalaires associés à un système linéaire d’équations (i.e., une équation matricielle) qui sont parfois aussi connues sous le nom de racines caractéristiques, valeurs caractéristiques (Hoffman et Kunze 1971), valeurs propres ou racines latentes (Marcus et Minc 1988, p. 144).

La détermination des valeurs propres et des vecteurs propres d’un système est extrêmement importante en physique et en ingénierie, où elle équivaut à la diagonalisation de la matrice et se pose dans des applications courantes comme l’analyse de stabilité, la physique des corps en rotation et les petites oscillations des systèmes vibrants, pour n’en citer que quelques-unes. Chaque valeur propre est appariée avec un vecteur dit propre correspondant (ou, en général, un vecteur propre droit correspondant et un vecteur propre gauche correspondant ; il n’y a pas de distinction analogue entre gauche et droite pour les valeurs propres).

La décomposition d’une matrice carrée en valeurs propres et vecteurs propres est connue dans cet ouvrage sous le nom de décomposition propre, et le fait que cette décomposition est toujours possible tant que la matrice constituée des vecteurs propres de est carrée est connu sous le nom de théorème de la décomposition propre.

L’algorithme de Lanczos est un algorithme de calcul des valeurs propres et des vecteurs propres pour de grandes matrices symétriques et peu nombreuses.

Disons que est une transformation linéaire représentée par une matrice . S’il existe un vecteur tel que

(1)

pour un certain scalaire , alors est appelée valeur propre de avec le vecteur propre (droit) correspondant .

Laissant être une matrice carrée

(2)

avec une valeur propre , alors les vecteurs propres correspondants satisfont

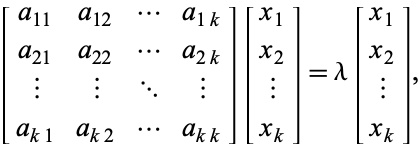(3)

ce qui est équivalent au système homogène

.

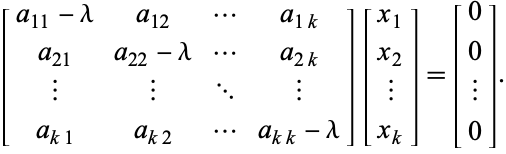(4)

L’équation (4) peut être écrite de manière compacte comme

(5)

où est la matrice d’identité. Comme le montre la règle de Cramer, un système linéaire d’équations a des solutions non triviales si le déterminant disparaît, donc les solutions de l’équation (5) sont données par

(6)

Cette équation est connue comme l’équation caractéristique de , et le côté gauche est connu comme le polynôme caractéristique.

Par exemple, pour une matrice , les valeurs propres sont

(7)

qui se présentent comme les solutions de la characteristicequation

(8)

Si toutes les valeurs propres sont différentes, alors en les rebranchant, on obtient équations indépendantes pour les composantes de chaque vecteur propre correspondant, et le système est dit non dégénéré. Si les valeurs propres sont -fois dégénérées, alors le système est dit dégénéré et les vecteurs propres ne sont pas linéairement indépendants. Dans ce cas, la contrainte supplémentaire que les vecteurs propres soient orthogonaux,

(9)

où est le delta de Kronecker, peut être appliquée pour donner des contraintes supplémentaires, permettant ainsi la solution pour les vecteurs propres.

Les valeurs propres peuvent être calculées dans le langage Wolfram en utilisant les valeurs propres. Les vecteurs propres et les valeurs propres peuvent être retournés ensemble en utilisant la commande Eigensystem.

Supposons que nous connaissions la valeur propre de

(10)

Ajout d’une constante fois la matrice identité à ,

(11)

de sorte que les nouvelles valeurs propres soient égales aux anciennes plus . En multipliant par une constante

(12)

alors les nouvelles valeurs propres sont les anciennes multipliées par .

Envisageons maintenant une transformation de similitude de . Soit le déterminant de , alors

.

			(13)
			(14)
			(15)

donc les valeurs propres sont les mêmes que pour .