A hónap novemberi tippjében (TOTM) 2011 novemberében egy esettanulmány kompresszorszámításokat mutattunk be. Összehasonlítottuk a szigorú módszer eredményeit a rövidített módszerek értékeivel. A szigorú módszer a Soave-Redlich-Kwong (SRK) típusú állapotegyenleten alapult a szükséges entalpiák és entrópiák kiszámításához. Az entalpiákat és entrópiákat a teljesítményszükséglet és a kisülési hőmérsékletek meghatározására használják. Az eredmények azt mutatták, hogy a rövidített módszer pontossága érzékeny az ideális gázállapot hőkapacitási arány k értékére.
Kizárólag számítási szempontból a teljesítményszámítás különösen érzékeny a tömegáram, a szívási hőmérséklet és nyomás, valamint a kiadási hőmérséklet és nyomás meghatározására. Egy kompresszor a teljesítményét befolyásoló változók változó értékei mellett fog működni. Így a kompresszor számításának legnehezebb része az egyes változók ésszerű tartományának meghatározása, és nem maga a számítás. A hivatkozás hangsúlyozza, hogy az egyes változók egyetlen értékének használata nem a helyes módja egy kompresszorrendszer értékelésének.
A termodinamikai számításokat általában ideális (reverzibilis) folyamatra végzik. A reverzibilis folyamat eredményeit ezután a termodinamikai hatásfok alkalmazásával a valós világhoz igazítják. A sűrítési folyamatban három ideális folyamatot lehet szemléltetni: 1) egy izotermikus folyamat (PV1=C1), 2) egy izentróp folyamat (PVk=C2) és 3) egy polytróp folyamat (PVn=C3). E folyamatok bármelyike alkalmasan felhasználható a kompressziós teljesítményigény kézi vagy számítógépes számítással történő értékelésének alapjául. Az izotermikus folyamatot azonban ritkán használják alapként, mivel a szokásos ipari sűrítési folyamatot még csak megközelítőleg sem állandó hőmérsékleten végzik.
Megjegyzendő, hogy a Dresser Rand elég sok munkát végez a “közel állandó hőmérsékletű” sűrítéssel, különösen a szellőzőkéményekből történő CO2-sűrítéssel. A részleteket lásd:
Ezzel a TOTM-mel bemutatjuk, hogyan lehet meghatározni egy kompresszor hatásfokát a mért áramlási sebesség, összetétel, szívó- és nyomóhőmérséklet és nyomás alapján. Egy szigorú, állapotegyenleten alapuló számítást és egy rövidített módszert veszünk figyelembe, és az eredményeket összehasonlítjuk.
Kompresszorhatásfok
A kompresszorok efficienciája a kompresszor típusától, méretétől és az átfolyástól függően változik. Ezek csak (utólag) kompresszorvizsgálattal határozhatók meg, bár a kompresszorgyártók általában jó becsléseket tudnak adni. Tervezési célokra a referencia a következő értékeket javasolja az általános efficienciákra:
1. táblázat. Kompresszorok összhatásfokai
|
Kompresszor típusa |
Hatékonyság, η |
|
Centrifugális |
0.70 – 0.85 |
|
Nagysebességű dugattyús |
0.72 – 0.85 |
|
Kissebességű dugattyús |
0.75 – 0,90 |
|
Pörgős csavaros |
0,65 – 0,75 |
A hivatkozás szerint ezek a teljes efficienciák tartalmazzák a kompresszoron belüli gázsúrlódást, a mechanikai veszteségeket (csapágyak, tömítések, sebességváltó stb.) és a sebességváltó veszteségeit. A mechanikai efficiencia a kompresszor méretétől és típusától függően változik, de a 95% hasznos tervezési szám. A kompresszor fej- és nyomóhőmérsékletének kiszámításakor az alkalmazott efficiencia izentróp vagy polytróp (az izentróp efficienciát néha adiabatikus efficienciának is nevezik). Ha az 1. táblázatban szereplő összes efficienciákhoz hozzáadunk 3-4 % efficienciát (mechanikai veszteségek), akkor általában jól becsülhető a termodinamikai efficiencia.
A meglévő kompresszor teljesítményének értékeléséhez a cél a kompresszor hatásfokának (η) és teljesítményigényének kiszámítása.
Az ismert és mért tulajdonságok:
a. Szabványos állapotban a gáz térfogatáram (qS) vagy a gáz tömegaránya ()
b. Gázösszetétel (zi)
c. Szívási nyomás (P1) és hőmérséklet (T1)
d. Kiáramlási nyomás (P2) és hőmérséklet (T2)
A hatásfok becslése – szigorú módszer
Minden kereskedelmi forgalomban kapható folyamatáramlás-szimulációs szoftver szíve egy állapotegyenlet. Egyszerűségük és viszonylagos pontosságuk miatt olyan köbös EOS-t használnak, mint a Soave Redlich-Kwong (SRK) vagy a Peng-Robinson. Ezeket az egyenleteket a gőz-folyadék-egyensúly (VLE), az entalpia (h) és az entrópia (s) kiszámítására használják. Megfelelő bináris kölcsönhatási együtthatókkal e két egyenlet folyamatszimulációs eredményei gyakorlatilag megegyeznek. Ezért ebben a munkában csak az SRK-t használjuk.
Az izentróp hatásfokot a következőképpen határozzuk meg:
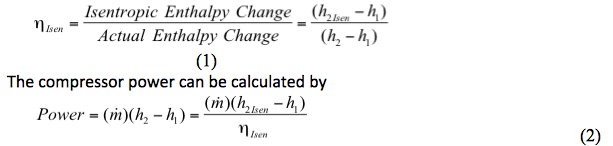
Hol:
ηIsen = izentróp hatásfok
h1 = P1, T1, és összetételnél (zi)
h2 = P2, T2-nél számított szívási entalpia, és összetétel (zi)
h2Isen = Izentróp kiadási entalpia P2 (vagy T2), S2Isen =S1, és összetétel (zi)
![]() = Tömegáram
= Tömegáram
A kompresszor hatásfokának vagy teljesítményének kiszámítása két lépésből áll
1. A kompressziós folyamat ideális vagy izentróp (reverzibilis és adiabatikus) entalpiaváltozásának (h2Isen-h1) meghatározása.
2. A tényleges entalpiaváltozás (h2-h1) meghatározása.
A lépésenkénti számítás egy EOS alapján:
a. Állandósult állapot feltételezése, azaz
b. Feltételezzük, hogy a takarmány összetétele változatlan marad
c. Számítsuk ki a szívási entalpiát h1=f(P1, T1 és zi) és az entrópiát s1=f(P1, T1 és zi) EOS
d. Tegyük fel izentróp folyamatot és állítsuk be s2Isen = f (P2, T2Isen, zi) = s1 = f (P1, T1, zi).
e. Számítsa ki az ideális entalpiát (h2Isen) kisülési állapotban ismert zi, T2 (vagy P2) és s2Isen esetén.
f. Számítsa ki a tényleges entalpiát (h2) kisülési állapotban ismert zi, T2 és P2 esetén.
g. Számítsa ki az izentróp hatásfokot az 1. egyenlet alapján: µIsen = (h2Isen – h1)/(h2 – h1)
h. Számítsa ki a teljesítményt a 2. egyenlet alapján: ![]()
A hatásfok becslése – Rövidített módszer
Az izentróp úti exponens (k) vagy az ideális gáz hőkapacitási aránya (k=CP/CV) a 2013. májusi TOTM-ben bemutatott összefüggés alapján számítható ki:
![]()
Hol:
T = hőmérséklet, K (°R)
![]() = gáz relatív sűrűsége; a gáz molekulatömegének aránya a levegő molekulatömegéhez
= gáz relatív sűrűsége; a gáz molekulatömegének aránya a levegő molekulatömegéhez
A = 0.000272 (0.000151)
A tényleges kisülési hőmérséklet izentróp pálya alapján becsülhető

Az izentróp hatásfok megoldásával,
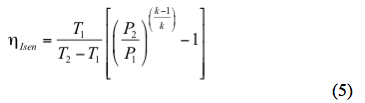
hasonlóan, a polytróp pályán alapuló tényleges kisülési hőmérséklet becsülhető

A fenti egyenletet a polytróp pálya együtthatójára (n) feloldva:

Hasonlóképpen, a polytróp pálya alapján becsülhető a tényleges kisülési hőmérséklet (ηPoly):

Az izentróp fejet a következő módon lehet kiszámítani:
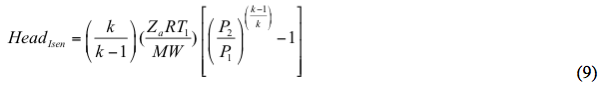
Hasonlóképpen, a polytróp fejet
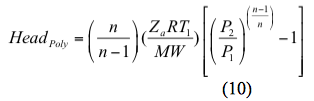
Egy izentróp (reverzibilis és adiabatikus) folyamat esetében a teljesítményt
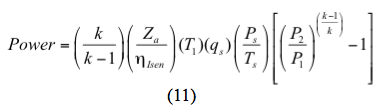
Vagy egy polytróp folyamat esetében a teljesítményt
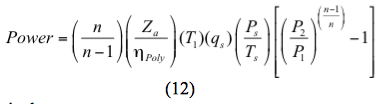
Alternatív módon:
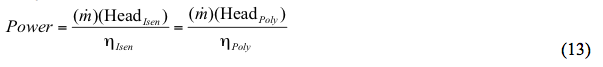
Ha:
Fülfejtés = Kompresszor fejmagasság, m (ft)
Teljesítmény = Kompresszor teljesítménye, kW (LE)
R = Univerzális gázállandó, 848 kg-m/(kmol-K) vagy (1545 ft-lbf/(lbmol-°R))
PS = Szabványos üzemi nyomás, kPa (psia)
P1 = Szívási nyomás, kPa (psia)
P2 = Kiürítési nyomás, kPa (psia)
TS = Szabványos hőmérséklet, K (°R)
T1 = Szívási hőmérséklet, K (°R)
T2 = Kiürítési hőmérséklet, K (°R)
qS = Gáz térfogatáram standard állapotban, Sm3/d (scf/nap)
Za = A gáz átlagos sűríthetőségi tényezője = (Z1+Z2)/2
Z1 = A gáz sűríthetőségi tényezője a szívási állapotban
Z2 = A gáz sűríthetőségi tényezője a kiadási állapotban
MW = A gáz molekulatömege
A teljesítményszámítást a sűrítési fokozatonként kell elvégezni, majd összegezni az egyetlen meghajtóhoz csatlakozó összes fokozatra.
A rövidített módszer lépésenkénti számítása
a. Számítsa ki az izentrópikus exponenciát (k) a 3. egyenlet alapján a T = (T1+3T2)/4 által meghatározott átlaghőmérséklet felhasználásával. Az átlaghőmérsékletnek ezt a formáját azért határoztuk meg, hogy jobb egyezést érjünk el a szigorú és a rövidített módszer eredményei között.
b. Számítsa ki az izentróp hatásfokot (ηIsen) az 5. egyenlet alapján.
c. Számítsa ki a polytropikus együtthatót (n) a 7. egyenlet alapján.
d. Számítsuk ki a polytróp hatásfokot (ηPoly) a 8.
e. egyenlet szerint. Számítsuk ki az izentróp és a polytróp fejek értékét a 9. és a 10. egyenlet segítségével.
f. Számítsa ki a szükséges teljesítményt fokozatonként a 11. vagy a 12. egyenlet segítségével.
Egy esettanulmány
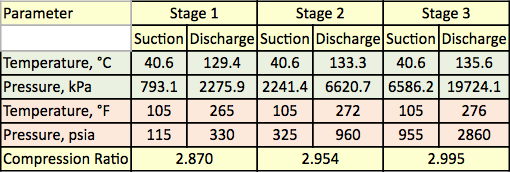
Egy földgázkeveréket háromfokozatú centrifugálkompresszorral sűrítünk. A folyamat áramlási diagramja az 1. ábrán látható. Az egyes fokozatoknál a mért nyomást, és hőmérsékletet az 1. táblázat mutatja be. A mért tápanyag-összetételt, az áramlási sebességeket, valamint a számított molekulatömeget és relatív sűrűséget a 2. táblázat mutatja be.
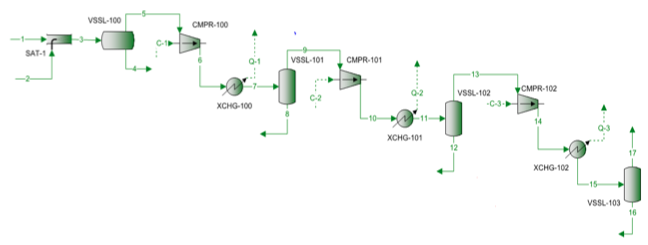
1. ábra. Folyamatáramlási diagram a 3 lépcsős sűrítéshez
1. táblázat. A mért hőmérséklet és nyomás a három fokozatú sűrítéshez
2. táblázat. Gázelemzés és áramlási sebesség a sűrítés három fokozatához
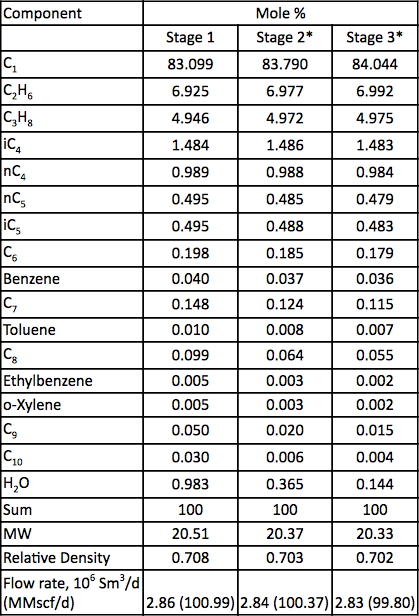
* Számított
Eredmények és viták
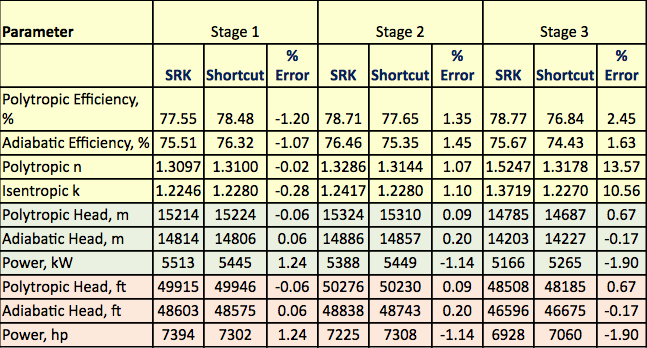
Az 1. ábrán látható folyamatáramlási diagramot a ProMax szoftverrel szimuláltuk a szigorú számítások elvégzéséhez az SRK EOS segítségével. A program kiszámította a polytróp és izentróp hatásfokokat, a fejlettségeket és a sűrítési teljesítményt. A program kiszámította az izentróp úti exponenciát (k) és a polytróp úti exponenciát (n) is. Ezeket a számított eredményeket a 2. táblázat tartalmazza mindhárom fokozatra vonatkozóan SRK címszó alatt. A ProMax által elvégzett számítások nagyon hasonlóak a szigorú szakaszban ismertetett a-h lépésről lépésre történő számításokhoz. A 2. táblázat a megfelelő értékekre vonatkozó rövidítéses számítási eredményeket is bemutatja a rövidítéses címszó alatt. A rövidített számítások a rövidített módszerről szóló részben ismertetett a-f lépésről-lépésre történő számításokon alapulnak. A 2. táblázatban a szigorú módszer és a rövidítéses módszerek közötti hibaszázalékot is bemutatjuk az egyes szakaszokra vonatkozóan. A 2. táblázat azt mutatja, hogy az 1. és 2. szakaszra kiváló egyezéseket kapunk. Nagyobb eltérések figyelhetők meg azonban a 3. szakasz izetropikus és polytropikus exponenseinél a nagynyomású működés miatt, amely túlságosan eltért az ideális gázállapot feltételeitől.
3. táblázat. A szigorú és a rövid úton számított eredmények összefoglalása
Következtetések
A 2. táblázat azt mutatja, hogy a rövid úton számított és a szigorú úton számított eredmények között jó az egyezés. A szigorú és a rövidített módszer eredményei közötti különbségek a létesítményszámítások és a tervezés szempontjából elhanyagolhatóak. A 3. szakasz esetében a nagynyomású működés és az ideális gázállapottól való túl nagy eltérés miatt nagyobb hiba figyelhető meg az izentropikus exponens (k) esetében.
A ProMaxban számított izentropikus exponens (k) nem az ideális gázállapot hőkapacitás (CP/CV) aránya. Ez az az izentrópiás exponens értéke, amely ahhoz szükséges, hogy izentróp útvonal jöjjön létre a bemenet és a kimenet között. Az értékét ennek az útvonalnak az integrálásával számítják ki. Így ez egyfajta “átlagos” érték, amely a valódi izentróp útvonalat képviseli. Ideális gázok esetében az érték egyenlő lenne a (CP/CV) aránnyal.
A “k” hibája azt is szemlélteti, hogy a teljesítményvizsgálat megrendelésekor milyen korrelációt kell használni (azaz további részletekért lásd az ASME PTC-10-et), hogy az ügyfél és a szállító a továbbiakban egyezségre jusson a vizsgált folyadék molekulatömegét (MW) és k értékét illetően. További részletekért lásd a referenciát és a 2010. augusztusi és szeptemberi TOTM-eket .
Az is érdemes megjegyezni, hogy az “n” és a polytropikus hatásfok tendenciája és a gép állapotának értékelése során a mérőműszerek/berendezések (hőmérséklet- és nyomásátalakítók) relatív pontossága és a kompresszor teljesítményének az eredeti teljesítménygörbére (tényleges gáz térfogatáram a sebesség függvényében) való leképezése számos lehetséges hibaforrást vezet be ebbe a napi értékelésbe.
Megjegyezzük, hogy a rövidítési módszerek pontossága a k és n értékeitől függ. Az átlaghőmérséklet definícióját a rövidített módszerben kiigazították, hogy a szigorú módszerrel számított izentróp úti exponens (k) jobban illeszkedjen.
Ha többet szeretne megtudni a hasonló esetekről és arról, hogyan lehet minimalizálni az üzemeltetési problémákat, javasoljuk, hogy vegyen részt a G4 (Gázkondicionálás és feldolgozás), PF4 (Olajtermelő és feldolgozó létesítmények), ME46 (Kompresszor rendszerek-mechanikai tervezés és specifikációk) és ME44 (Szivattyú- és kompresszorrendszerek alapjai), tanfolyamainkon.
A PetroSkills tanácsadói szakértelmet kínál ebben és sok más témában. Ha további információt szeretne kapni ezekről a szolgáltatásokról, látogasson el weboldalunkra a http://petroskills.com/consulting címen, vagy írjon nekünk a [email protected] e-mail címre.
Dr. Mahmood Moshfeghian
Hivatkozás:
3. Soave, G., Chem. Eng. Sci., Vol. 27, pp. 1197-1203, 1972.
4. Peng, D. Y., and Robinson, D. B., Ind. Eng. Chem. Fundam., Vol. 15, p. 59, 1976.
5. ProMax 3.2, Bryan Research and Engineering, Inc, Bryan, Texas, 2014.
6. ASME PTC-10, “Performance test Code on Compressors and Exhausters”, 1997.
7. Honeywell, J. “A centrifugálkompresszorok vizsgálatának fontos szempontjai – 1. rész”, A hónap tippje, 2010. augusztus
8. Honeywell, J. “A centrifugálkompresszorok vizsgálatának fontos szempontjai – 2. rész”, A hónap tippje, 2010. szeptember
.