A P-Only szabályozóhoz hasonlóan az arányos-integrál (PI) algoritmus is kiszámítja és minden T mintavételi időnként továbbítja a szabályozó kimeneti (CO) jelét a végső szabályozó elemnek (pl. szelep, változó fordulatszámú szivattyú). A PI-algoritmus által kiszámított CO-t a szabályozó hangolási paraméterei és a szabályozó hibája, e(t) befolyásolja.
A PI-szabályozók két hangolási paramétert állítanak be. Bár emiatt nagyobb kihívást jelent a hangolásuk, mint a csak P-szabályozóké, nem olyan bonyolultak, mint a három paraméteres PID-szabályozók.
Az integrálhatás lehetővé teszi a PI-szabályozók számára az eltolás kiküszöbölését, ami a csak P-szabályozók egyik fő gyengesége. Így a PI-szabályozók olyan egyensúlyt biztosítanak a bonyolultság és a képességek között, amely miatt messze a legszélesebb körben használt algoritmusok a folyamatszabályozási alkalmazásokban.
A PI-algoritmus
Míg a különböző gyártók különböző formákba öntik a lényegében ugyanazt az algoritmust, itt azt vizsgáljuk meg, amit különbözőképpen függő, ideális, folytonos, pozíció formaként írnak le:
![]()
Hol:
CO = a szabályozó kimeneti jele (a kimenő vezeték)
CObias = a szabályozó előfeszítése vagy nulla értéke; az alább ismertetett bumpless átvitellel állítható be
e(t) = aktuális szabályozó hiba, SP – PV
SP = beállított pont
PV = mért folyamatváltozó (a vezeték befelé)
Kc = szabályozó erősítése, egy hangolási paraméter
Ti = visszaállítási idő, egy hangolási paraméter
Az egyenlőségjel jobb oldalán lévő első két kifejezés megegyezik a cikk elején hivatkozott P-Only szabályozóval.
A szabályozó integrál üzemmódja az egyenlet utolsó tagja. Feladata a szabályozó hibájának, e(t), időbeli integrálása vagy folyamatos összegzése.
Egy pár dolgot érdemes tudni a visszaállítási idő hangolási paraméterről, Ti:
| ▪ | Ez külön súlyt ad az integrálterminusnak, így az integrálhatás hatása önállóan beállítható. |
| ▪ | A nevezőben van, így a kisebb értékek nagyobb súlyt biztosítanak (pl. növelik az integrál kifejezés hatását. |
| ▪ | Ez időegységgel rendelkezik, így mindig pozitív. |
A proporcionális terminus függvénye
A csak P-szabályozóhoz hasonlóan a PI-szabályozó Kc-e(t) arányos terminusa minden t időpontban a szabályozó e(t) hibájának nagysága alapján hozzáad vagy kivon a CObiasból.
Amint e(t) nő vagy csökken, a CObiashoz hozzáadott összeg azonnal és arányosan nő vagy csökken. A szabályozó hibájának előzményei és aktuális pályája nincs hatással az arányos kifejezés kiszámítására.
Az alábbi ábra (kattintson a nagyméretű nézetért) szemlélteti ezt az elképzelést a beállított pontra adott válaszra. Az arányos számításhoz használt hiba látható a grafikonon:
▪ A t = 25 perc időpontban e(25) = 60-56 = 4
▪ A t = 40 perc időpontban e(40) = 60-62 = -2
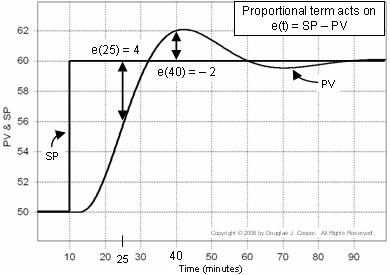
Megismételve, hogy a szabályozó hibája e(t) = SP – PV, ahelyett, hogy a PV-t és az SP-t különálló nyomvonalaknak tekintenénk, mint fent, kiszámíthatjuk és ábrázolhatjuk az e(t)-t a t időpont minden egyes pontján.
Az alábbiakban (kattintson a nagyméretű nézetért) a fenti adatokkal megegyező adatok láthatók, csak magának az e(t)-nek az ábrázolásaként. Vegyük észre, hogy a fenti ábrán a PV = SP = 50 az első 10 percben, míg az alábbi hibadiagramon e(t) = 0 ugyanebben az időszakban.
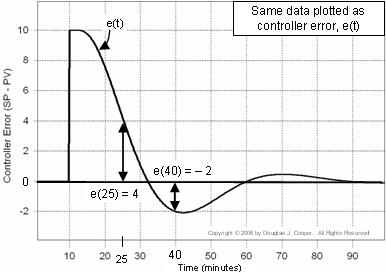
Ez az ábra azért hasznos, mert segít szemléltetni, hogyan változik folyamatosan a szabályozó hibájának mérete és előjele az idő múlásával.
Az integrál kifejezés függvénye
Míg az arányos kifejezés csak a szabályozó számításának időpontjában veszi figyelembe az e(t) aktuális nagyságát, addig az integrál kifejezés a hiba előzményeit veszi figyelembe, vagyis azt, hogy a mért folyamatváltozó mennyi ideig és milyen messze volt a beállított ponttól az idők folyamán.
Az integrálás egy folyamatos összegzés. A hiba időbeli integrálása azt jelenti, hogy a szabályozó teljes hibatörténetét összegezzük a jelen időpontig, attól kezdve, hogy a szabályozót először kapcsoltuk automatikára.
A szabályozó hibája e(t) = SP – PV. Az alábbi ábrán (kattintson a nagyméretű nézetért) a hiba integrálösszegét az SP és PV nyomvonalak közötti árnyékolt területként számoljuk ki.
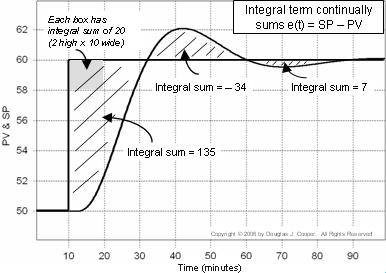
A diagram minden egyes dobozában az integrálösszeg 20 (2 magas és 10 széles). Ha megszámoljuk az árnyékolt területeken található dobozok számát (beleértve a dobozok töredékeit is), kiszámíthatjuk a hiba integrálösszegét.
Amikor tehát a PV először lépi át a beállított pontot t = 32 körül, az integrálösszeg már körülbelül 135-re nőtt. A PI-szabályozó integráltermét így írjuk fel:
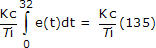
Mivel a számítást a szabályozó hibája irányítja, az alábbiakban látható (a nagyméretű nézetért kattintsunk) szabályozóhiba-diagramból közvetlen képet kapunk a helyzetről:

Megjegyezzük, hogy az egyes árnyékolt részek integrálja a hibával azonos előjelű. Mivel az integrálösszeg akkor kezd felhalmozódni, amikor a szabályozó először kerül automatikus üzemmódba, a teljes integrálösszeg növekszik, amíg e(t) pozitív, és zsugorodik, amikor negatív.
A grafikonokon a t = 60 perc időpillanatban az integrálösszeg 135 – 34 = 101. A válasz t = 90 percnél nagyrészt rendeződik, és az integrálösszeg ekkor 135 – 34 + 7 = 108.
Az integrálhatás megszünteti az eltolódást
Az előző mondat egy finom, de nagyon fontos megfigyelést tesz. A válasz nagyrészt teljes a t = 90 perc időpontban, mégis az összes hiba integrálösszege nem nulla.
Ebben a példában az integrálösszeg végső vagy maradék értéke 108. Ez a maradékérték az, ami lehetővé teszi a PI-szabályozó integrálhatását az eltolás megszüntetésére.
Amint azt egy korábbi cikkünkben tárgyaltuk, a legtöbb, csak P-szabályozással működő folyamatnál a normál működés során eltolás tapasztalható. Az offset a szabályozó hibájának tartós értéke (azaz a PV nem egyenlő az SP-vel állandósult állapotban).
A P-Only szabályozóból felismerjük:
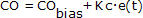
hogy a CO mindig egyenlő lesz a CObiával, hacsak nem adunk hozzá vagy vonunk le belőle valamit.
A fenti P-Only egyenletben csak akkor van mit hozzáadni vagy levonni a CObiából, ha e(t) nem nulla. Ha e(t) nem állandóan nulla, akkor a PV nem egyenlő az SP-vel, és van offsetünk.
A PI szabályozóval azonban:
![]()
már tudjuk, hogy az integrál hibaösszegnek lehet egy végső vagy maradék értéke a válaszadás befejezése után. Ez azért fontos, mert ez azt jelenti, hogy e(t) lehet nulla, mégis lehet valami, amit hozzáadhatunk vagy kivonhatunk a CObiasból, hogy kialakítsuk a szabályozó végső kimenetét, a CO-t.
Amíg tehát van bármilyen hiba (amíg e(t) nem nulla), az integrál kifejezés mérete nő vagy csökken, hogy hatással legyen a CO-ra. A CO változásai csak akkor szűnnek meg, ha a PV tartósan egyenlő SP-vel (amikor e(t) = 0).
Az integrálterminusnak ekkor lehet maradványértéke, ahogy azt az imént tárgyaltuk. Ez az integrálásból származó maradékérték, amikor hozzáadódik a CObias-hoz, lényegében egy új teljes torzítási értéket hoz létre, amely megfelel az új működési szintnek.
Az integrálhatás valójában folyamatosan visszaállítja a torzítási értéket az eltolás kiküszöbölésére, ahogy a működési szint változik.
A PI-szabályozás kihívásai
A PI-algoritmus alkalmazása során vannak kihívások:
| ▪ | A két hangolási paraméter kölcsönhatásban van egymással, és a tervezőnek ki kell egyensúlyoznia a hatásukat. |
| ▪ | Az integrál kifejezés hajlamos növelni a folyamatválasz oszcillációs vagy gördülő viselkedését. |
Mivel a két hangolási paraméter kölcsönhatásba lép egymással, kihívást jelenthet a “legjobb” hangolási értékek elérése. Tervezési és hangolási receptünk értéke és fontossága növekszik, ahogy a szabályozó egyre összetettebbé válik.
A szabályozó inicializálása az ütközésmentes átvitelhez
Amikor bármilyen szabályozót kézi üzemmódból automatikusra (nyitott hurokból zárt hurokba) kapcsolunk, azt szeretnénk, ha az eredmény eseménytelen lenne. Vagyis nem akarjuk, hogy az átkapcsolás olyan hirtelen szabályozási műveleteket okozzon, amelyek befolyásolják vagy megzavarják a folyamatunkat
Az átkapcsoláskor ezt a kívánt eredményt úgy érjük el, hogy a szabályozó integrál hibaösszegét nullára inicializáljuk. Továbbá a beállítási pontot és a szabályozó előfeszítési értékét úgy inicializáljuk, hogy beállítjuk:
▪ SP egyenlő az aktuális PV-vel
▪ CObias egyenlő az aktuális CO-val
Mivel az integrál hibaösszeg nullára van állítva, nincs semmi olyan hozzáadandó vagy kivonandó a CObiasból, ami hirtelen változást okozna az aktuális szabályozó kimenetében. Ha a beállított pont megegyezik a mért folyamatváltozóval, nincs olyan hiba, amely a CO-unkban változást okozna. És mivel a szabályozó előfeszítése az aktuális CO-értékünkre van beállítva, alapértelmezés szerint fel vagyunk készülve az aktuális működés fenntartására.
Így, amikor kézi üzemmódból automatikus üzemmódra váltunk, “ütközésmentes átállás” van, meglepetés nélkül. Ezt az eredményt mindenki értékeli.
A visszaállítási idő kontra visszaállítási sebesség
A különböző gyártók kissé eltérő formába öntik a vezérlőalgoritmusaikat. Néhányan arányos sávot használnak a szabályozó erősítése helyett. Valamint egyesek reset rate, Tr, reset time helyett reset time-ot használnak. Ezek egyszerűen egymás inverzei:
Tr = 1/Ti
Nem számít, hogyan fejezik ki a hangolási paramétereket, a PI-algoritmusok mind egyformán alkalmasak.
De nagyon fontos, hogy ismerje a gyártóját, mielőtt elkezdi hangolni a szabályozóját, mert a paraméterértékeket az adott algoritmusformához kell igazítani.A szabályozók tervezéséhez és hangolásához használt kereskedelmi szoftverek automatikusan megoldják ezt a problémát az Ön számára.
PI-szabályozó megvalósítása
Ebben a cikkben a PI-szabályozó tervezését, hangolását és megvalósítását vizsgáljuk meg a hőcserélőn és a gravitációsan leeresztett tartályokon.
Ebben a cikkben a PI-szabályozó tervezését, hangolását és megvalósítását vizsgáljuk.