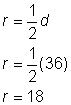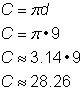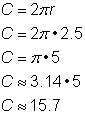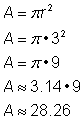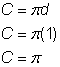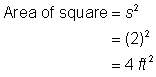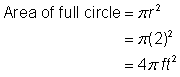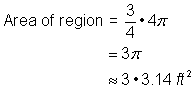Körök
Tanulási cél(ok)
– A körök tulajdonságainak azonosítása.
– A kör kerületének meghatározása.
– Meghatározza a kör területét.
– Meghatározza az összetett geometriai alakzatok területét és kerületét.
Bevezetés
A kör egy gyakori alakzat. Mindenütt látod őket – az autók kerekei, a levegőben repülő frizbik, az adatokat szállító kompaktlemezek. Ezek mind körök.
A kör ugyanúgy kétdimenziós alakzat, mint a sokszögek és a négyszögek. A köröket azonban másképp mérjük, mint ezeket a többi alakzatot – még néhány más kifejezést is használnunk kell a leírásukra. Nézzük meg ezt az érdekes alakzatot.
A körök tulajdonságai
A kör olyan pontok halmazát ábrázolja, amelyek mindegyike azonos távolságra van egy rögzített, középső ponttól. Ezt a fix pontot nevezzük középpontnak. A kör középpontjától a kör bármely pontjáig mért távolságot a kör sugarának nevezzük.
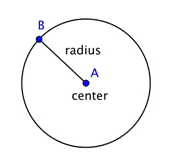
Ha két sugarat (a sugár többes száma) összeillesztünk, hogy egy, a kört átszelő vonalszakaszt alkossunk, akkor átmérőt kapunk. Egy kör átmérője a kör középpontján halad át, és végpontjai magán a körön vannak.
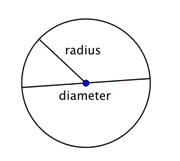
Minden kör átmérője a kör sugarának kétszerese. Ezt a 2r, azaz “a sugár kétszerese” kifejezéssel lehet ábrázolni. Tehát ha ismered egy kör sugarát, akkor megszorozhatod 2-vel, hogy megtaláld az átmérőjét; ez azt is jelenti, hogy ha ismered egy kör átmérőjét, akkor eloszthatod 2-vel, hogy megtaláld a sugarát.
|
Példa |
||
|
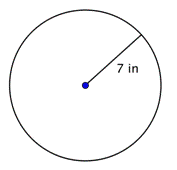
Probléma |
Keresd meg a kör átmérőjét.
|
|
|
d = 2r d = 2(7) d = 14 |
Az átmérő a sugár kétszerese, vagyis 2r. Ennek a körnek a sugara 7 hüvelyk, tehát az átmérője 2(7) = 14 hüvelyk. |
|
|
Válasz |
Az átmérő 14 hüvelyk. |
|
|
Példa |
||
|
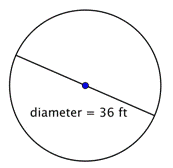
Probléma |
Meg kell találni a kör sugarát.
|
|
|
|
A sugár az átmérő fele, vagyis |
|
|
Válasz |
A sugár 18 láb. |
|
Körfogat
A kör kör körüli távolságot kerületnek nevezzük. (Emlékezzünk vissza, egy sokszög körüli távolság a kerület.)
A körök egyik érdekes tulajdonsága, hogy a kör kerületének és átmérőjének aránya minden kör esetében azonos. Nem számít, hogy mekkora a kör mérete, a kerület és az átmérő aránya ugyanaz lesz.
Az alábbiakban különböző tárgyak néhány tényleges méretét adjuk meg. A mérések milliméteres vagy negyed hüvelykes pontosságúak (a használt mértékegységtől függően). Nézd meg mindegyiknél a kerület és az átmérő arányát – bár a tárgyak különbözőek, az arány mindegyiknél megközelítőleg ugyanaz.
|
Tétel |
Kerület (C) (a legközelebbi századrészre kerekítve) |
átmérő (d) |
arány |
|
Cup |
253 mm |
79 mm |
|
|
negyed |
8484 mm |
27 mm |
|
|
Tál |
37.25 in |
11.75 in |
|
A kerület és az átmérő hozzávetőleges méretek, mivel nincs pontos mód ezen méretek pontos mérésére. Ha azonban pontosabban meg tudnád mérni őket, akkor azt találnád, hogy a ![]() arány a megadott elemek mindegyikénél a 3,14 felé mozdulna el. A
arány a megadott elemek mindegyikénél a 3,14 felé mozdulna el. A ![]() arány matematikai neve pi, és a görög
arány matematikai neve pi, és a görög ![]() betűvel jelölik.
betűvel jelölik.
![]() egy nem végződő, nem ismétlődő tizedesjegy, ezért nem lehet teljesen kiírni. A
egy nem végződő, nem ismétlődő tizedesjegy, ezért nem lehet teljesen kiírni. A ![]() első 10 számjegye 3,141592653; ezt gyakran 3,14-re kerekítik, vagy
első 10 számjegye 3,141592653; ezt gyakran 3,14-re kerekítik, vagy ![]() törtként becsülik. Megjegyezzük, hogy mind a 3,14, mind a
törtként becsülik. Megjegyezzük, hogy mind a 3,14, mind a ![]() a
a ![]() közelítése, és olyan számításoknál használják, ahol nem fontos a pontosság.
közelítése, és olyan számításoknál használják, ahol nem fontos a pontosság.
Mivel tudjuk, hogy a kerület és az átmérő hányadosa (vagy ![]() ) minden kör esetében állandó, ezt a számot használhatjuk egy kör kerületének megkeresésére, ha ismerjük az átmérőjét.
) minden kör esetében állandó, ezt a számot használhatjuk egy kör kerületének megkeresésére, ha ismerjük az átmérőjét.
![]() =
= ![]() , tehát C =
, tehát C = ![]() d
d
Aminthogy d = 2r, akkor C = ![]() d =
d = ![]() (2r) = 2
(2r) = 2![]() r.
r.
Kör kerülete
A kör kerületének (C) kiszámításához használjuk a következő képletek egyikét:
Ha ismerjük a kör átmérőjét (d): ![]()
Ha ismered a kör sugarát (r): ![]()
|
Példa |
||
|
Probléma |
Keresd meg a kör kerületét.
|
|
|
|
A kör kerületének kiszámításához, ha az átmérő 9 hüvelyk, használd a Mivel a |
|
|
Válasz |
A kerület 9 |
|
|
Példa |
||
|
Probléma |
Következtessük egy 2 sugarú kör kerületét.5 yard. |
|
|
|
A 2,5 yard sugarú kör kerületének kiszámításához használjuk a |
|
|
Válasz |
A kerület 5 |
|
A kör sugara 8 inch. Mekkora a kerülete, a legközelebbi hüvelykre kerekítve?
A) 25 hüvelyk
B) 50 hüvelyk
C) 64 hüvelyk2
D) 201 hüvelyk
A terület
![]() a geometriában fontos szám. Már használtad egy kör kerületének kiszámításához. A
a geometriában fontos szám. Már használtad egy kör kerületének kiszámításához. A ![]() -t akkor is használod, amikor egy kör területét számolod ki.
-t akkor is használod, amikor egy kör területét számolod ki.
Kör területe
A kör területének (A) kiszámításához használd a képletet: ![]()
|
Példa |
||
|
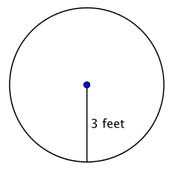
Probléma |
A kör területének meghatározása.
|
|
|
|
A kör területének kiszámításához használd a Ne feledd, hogy a választ négyzetmértékegységben írd, hiszen a területet keresed. |
|
|
Válasz |
A terület 9 |
|
A gomb átmérője 20 milliméter. Mekkora a gomb területe? Használd a 3,14-es értéket közelítőleg ![]() .
.
A) 62,8 mm
B) 314 mm2
C) 400 mm2
D) 1256 mm2
Összetett alakzatok
Most már tudod, hogyan kell kiszámítani a kör kerületét és területét, ezt a tudást felhasználhatod összetett alakzatok kerületének és területének kiszámításához. Az ilyen típusú feladatok megoldásának trükkje az, hogy az összetett alakzaton belül azonosítod az alakzatokat (és az alakzatok részeit), kiszámítod az egyes méreteiket, majd összeadod őket.
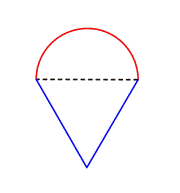
Nézd meg például az alábbi képet. Meg lehet-e találni a kerületét?
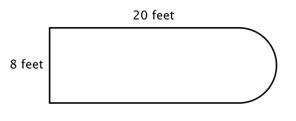
Az első lépés az, hogy az összetett ábrán belül azonosítsuk az egyszerűbb alakzatokat. Egy téglalapra és egy félkörre bonthatod, ahogy az alábbiakban látható.
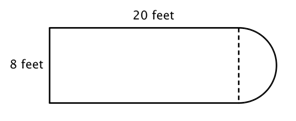
Tudod, hogyan találd meg egy téglalap kerületét, és tudod, hogyan találd meg egy kör kerületét. Itt a téglalap három tömör oldalának kerülete 8 + 20 + 20 = 48 láb. (Figyeljük meg, hogy a téglalapnak csak három oldala adódik össze az összetett alakzat kerületéhez, mert a másik oldal nem egy élnél van; azt a félkör fedi!)
A félkör kerületének megkereséséhez használjuk a ![]() képletet 8 láb átmérővel, majd az eredmény felét vesszük. A félkör kerülete
képletet 8 láb átmérővel, majd az eredmény felét vesszük. A félkör kerülete ![]() , azaz körülbelül 12,56 láb, így a teljes kerület körülbelül 60,56 láb.
, azaz körülbelül 12,56 láb, így a teljes kerület körülbelül 60,56 láb.
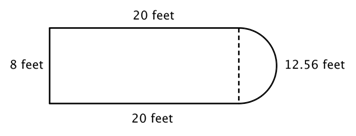
|
Példa |
||
|
Probléma |
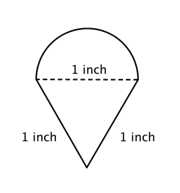
Keresd meg a félkörből és egy háromszögből álló összetett alakzat kerületét (a legközelebbi századrészre).
|
|
|
|
Az összetett alakzaton belüli kisebb alakzatok azonosítása. Ez az ábra egy félkört és egy háromszöget tartalmaz. |
|
|
Az átmérő (d) = 1
A félkör kerülete = |
Keresd meg a kör kerületét. Ezután osszuk el 2-vel, hogy megtaláljuk a félkör kerületét. |
|
|
|
|
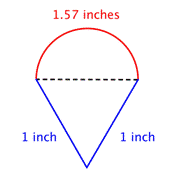
A félkör kerületének és a két láb hosszának összeadásával megkapjuk a teljes kerületet. Mivel a félkör kerületének a méréseink közelítőek, a kerület is közelítő lesz. |
|
Válasz |
Nagyságrendileg 3 db.57 hüvelyk |
|
|
Példa |
||
|
Probléma |
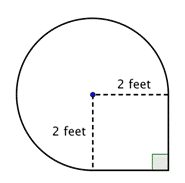
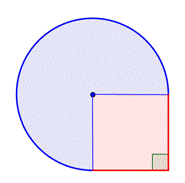
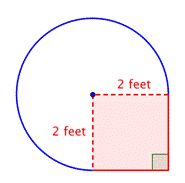
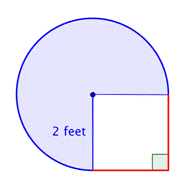
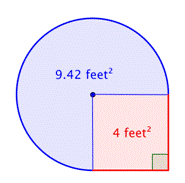
Következtesse az összetett ábra területét, háromnegyed körből és egy négyzetből álló alakzatot a legközelebbi század rész pontossággal.
|
|
|
|
Kisebb alakzatok azonosítása az összetett ábrán belül. Ez az ábra egy kör alakú területet és egy négyzetet tartalmaz. Ha mindkettő területét megtalálod, meg tudod találni az egész ábra területét. |
|
|
|
Keresd meg a négyzet területét. |
|
|
|
|
Keresd meg a kör alakú terület területét. A sugár 2 láb. Megjegyezzük, hogy a terület |
|
|
4 láb2 + |
Add össze a két régiót. Mivel a kör alakú kör területének mérése közelítő, az ábra területe is közelítő lesz. |
|
Válasz |
A terület megközelítőleg 13.42 láb2. |
|
Mekkora az alábbi ábrán látható alakzat területe (a legközelebbi századrészre)? (Mindkét lekerekített terület félkör.)
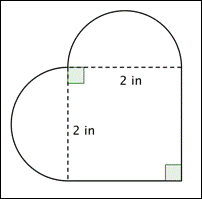
A) 16,56 in2
B) 7,14 in2
C) 4 in2
D) 3.14 in2
Summary
A kör egy fontos geometriai alakzat. A kör körüli távolságot kerületnek, a kör belső terét pedig területnek nevezzük. A kör kerületének és területének kiszámításához egy pi (![]() ) nevű számra van szükség, amely egy nem végződő, nem ismétlődő tizedesjegy. A pi-t gyakran a 3,14 és a
) nevű számra van szükség, amely egy nem végződő, nem ismétlődő tizedesjegy. A pi-t gyakran a 3,14 és a ![]() értékekkel közelítik. Összetett alakzatok – beleértve a kör alakú részeket tartalmazó alakzatokat is – kerületét vagy területét a kerület és terület képletének megfelelő alkalmazásával határozhatod meg.
értékekkel közelítik. Összetett alakzatok – beleértve a kör alakú részeket tartalmazó alakzatokat is – kerületét vagy területét a kerület és terület képletének megfelelő alkalmazásával határozhatod meg.