Cele nauczania
- Zrozumieć trójwymiarową reprezentację orbitali elektronicznych
Orbital jest kwantowo-mechanicznym udoskonaleniem orbity Bohra. W przeciwieństwie do jego koncepcji prostego orbitalu kołowego o stałym promieniu, orbitale są matematycznie wyprowadzonymi regionami przestrzeni o różnym prawdopodobieństwie zawarcia elektronu.
Jeden ze sposobów reprezentacji rozkładu prawdopodobieństwa elektronów został zilustrowany wcześniej na orbitalu 1s wodoru. Ponieważ Ψ2 daje prawdopodobieństwo znalezienia elektronu w danej objętości przestrzeni (takiej jak pikometr sześcienny), wykres Ψ2 w zależności od odległości od jądra (r) jest wykresem gęstości prawdopodobieństwa. Orbital 1s jest sferycznie symetryczny, więc prawdopodobieństwo znalezienia elektronu 1s w dowolnym punkcie zależy tylko od jego odległości od jądra. Gęstość prawdopodobieństwa jest największa w punkcie \(\) = 0\) (w jądrze) i maleje systematycznie wraz z odległością. Przy bardzo dużych wartościach r, gęstość prawdopodobieństwa elektronu jest bardzo mała, ale nie zerowa.
Dla kontrastu, możemy obliczyć prawdopodobieństwo radialne (prawdopodobieństwo znalezienia elektronu 1s w odległości \(r\) od jądra) dodając razem prawdopodobieństwa elektronu znajdującego się we wszystkich punktach serii x sferycznych powłok o promieniach r1, r2, r3,…, rx – 1, rx. W rezultacie, dzielimy atom na bardzo cienkie koncentryczne powłoki, tak jak warstwy cebuli (Rysunek \) i obliczamy prawdopodobieństwo znalezienia elektronu na każdej sferycznej powłoce. Przypomnijmy, że gęstość prawdopodobieństwa elektronów jest największa przy \(r) = 0 (Rysunek \(\PageIndex{1b}}), więc gęstość kropek jest największa dla najmniejszych powłok sferycznych w części (a) na Rysunku \(\PageIndex{1}}. Z drugiej strony, powierzchnia każdej kulistej powłoki jest równa \(4πr^2\), która rośnie bardzo szybko wraz ze wzrostem \(r) (Rysunek \(\PageIndex{1c}}). Ponieważ powierzchnia powłok sferycznych rośnie szybciej ze wzrostem \(r) niż gęstość prawdopodobieństwa elektronów maleje, wykres prawdopodobieństwa radialnego ma maksimum w pewnej szczególnej odległości \(r) (Rysunek \(\PageIndex{1d}}). Najważniejsze jest to, że kiedy \(r) jest bardzo małe, powierzchnia powłoki sferycznej jest tak mała, że całkowite prawdopodobieństwo znalezienia elektronu w pobliżu jądra jest bardzo małe; przy jądrze prawdopodobieństwo elektronu znika (Rysunek \(\PageIndex{1d}}).

Przy atomie wodoru, szczyt w wykresie prawdopodobieństwa radialnego występuje przy \(r\) = 0.529 Å (52.9 pm), który jest dokładnie promieniem obliczonym przez Bohra dla orbity n = 1. Tak więc najbardziej prawdopodobny promień otrzymany z mechaniki kwantowej jest identyczny z promieniem obliczonym przez mechanikę klasyczną. W modelu Bohra zakładano jednak, że elektron znajduje się w tej odległości przez 100% czasu, podczas gdy w modelu Schrödinga znajduje się on w tej odległości tylko przez pewien czas. Różnica pomiędzy tymi dwoma modelami wynika z falowego zachowania elektronu i zasady nieoznaczoności Heisenberga.
Rysunek porównuje gęstości prawdopodobieństwa elektronów na orbitalach 1s, 2s, i 3s wodoru. Zauważ, że wszystkie trzy są sferycznie symetryczne. W przypadku orbitali 2s i 3s, jakkolwiek (i w przypadku wszystkich innych orbitali s również), gęstość prawdopodobieństwa elektronów nie spada gładko wraz ze wzrostem \(r). Zamiast tego, obserwuje się serię minimów i maksimów w radialnych wykresach prawdopodobieństwa (Rysunek \(\PageIndex{2c}}). Minima odpowiadają kulistym węzłom (regionom zerowego prawdopodobieństwa elektronowego), które przeplatają się z kulistymi regionami niezerowego prawdopodobieństwa elektronowego. Istnienie tych węzłów jest konsekwencją zmian fazy falowej w funkcji falowej Ψ.
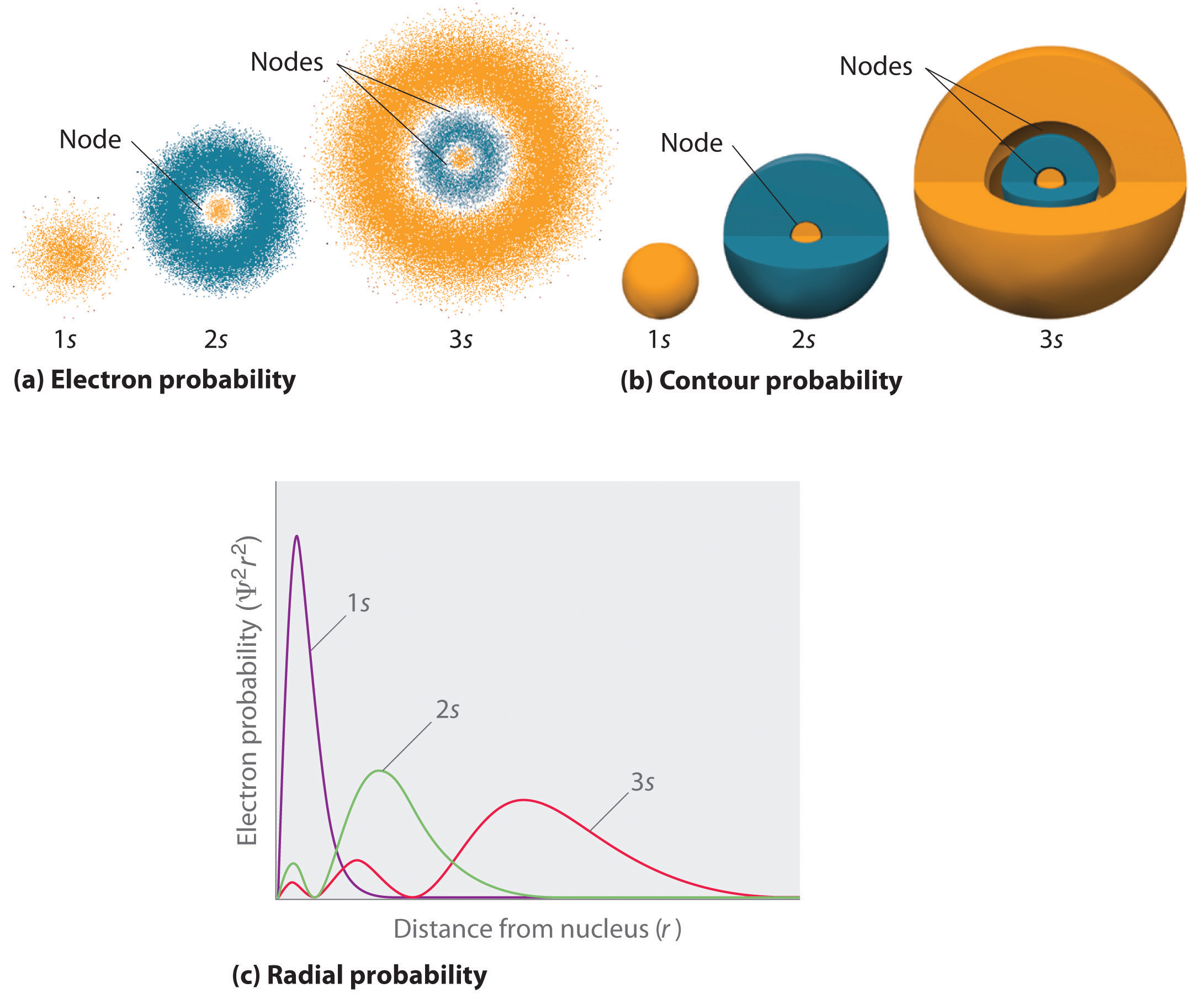
Orbitale s (l=0)
Trzy rzeczy dzieją się z orbitalami s wraz ze wzrostem n (Rysunek \\):
- Stają się większe, rozciągając się dalej od jądra.
- Zawierają więcej węzłów. Jest to podobne do fali stojącej, która ma regiony o znacznej amplitudzie oddzielone węzłami, punktami o zerowej amplitudzie.
- Dla danego atomu, orbitale s również stają się bardziej energetyczne wraz ze wzrostem n z powodu zwiększonej odległości od jądra.
Orbitale są ogólnie rysowane jako trójwymiarowe powierzchnie, które obejmują 90% gęstości elektronowej, jak pokazano dla 1s, 2s i 3s orbitali wodoru w części (b) na rysunku. Chociaż takie rysunki pokazują względne rozmiary orbitali, zwykle nie pokazują sferycznych węzłów na orbitalach 2s i 3s, ponieważ sferyczne węzły leżą wewnątrz 90% powierzchni. Na szczęście, pozycje węzłów sferycznych nie są ważne dla wiązania chemicznego.
p Orbitale (l=1)
Tylko orbitale s są sferycznie symetryczne. Wraz ze wzrostem wartości l, liczba orbitali w danej podpowłoce wzrasta, a kształty orbitali stają się bardziej złożone. Ponieważ podpowłoka 2p ma l = 1, przy trzech wartościach ml (-1, 0, i +1), istnieją trzy orbitale 2p.
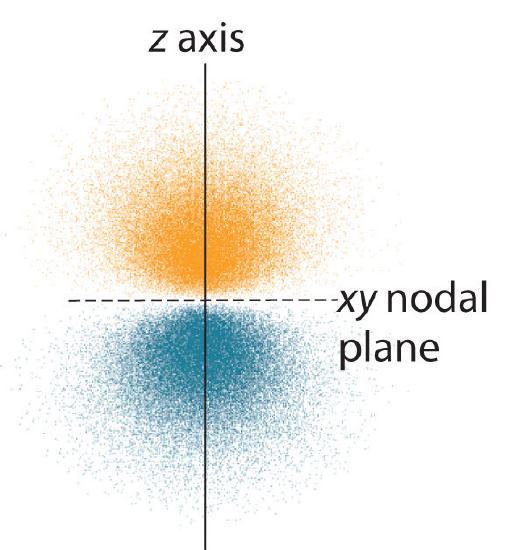
Rozkład prawdopodobieństwa elektronów dla jednego z orbitali 2p wodoru jest pokazany na rysunku rzedu. Ponieważ orbital ten ma dwa płaty gęstości elektronowej rozmieszczone wzdłuż osi z, z gęstością elektronową równą zero w płaszczyźnie xy (tj. płaszczyzna xy jest płaszczyzną węzłową), jest to orbital \(2p_z\). Jak pokazano na rysunku, pozostałe dwa orbitale 2p mają identyczny kształt, ale leżą odpowiednio wzdłuż osi x (2p_x) i y (2p_y). Zauważmy, że każdy orbital p ma tylko jedną płaszczyznę węzłową. W każdym przypadku faza funkcji falowej fo każdego z orbitali 2p jest dodatnia fo płatów skierowanych wzdłuż osi dodatniej i ujemna fo płatów skierowanych wzdłuż osi ujemnej. Należy podkreślić, że znaki te odpowiadają fazie fali opisującej ruch elektronu, a nie dodatnim ładunkom ujemnym.
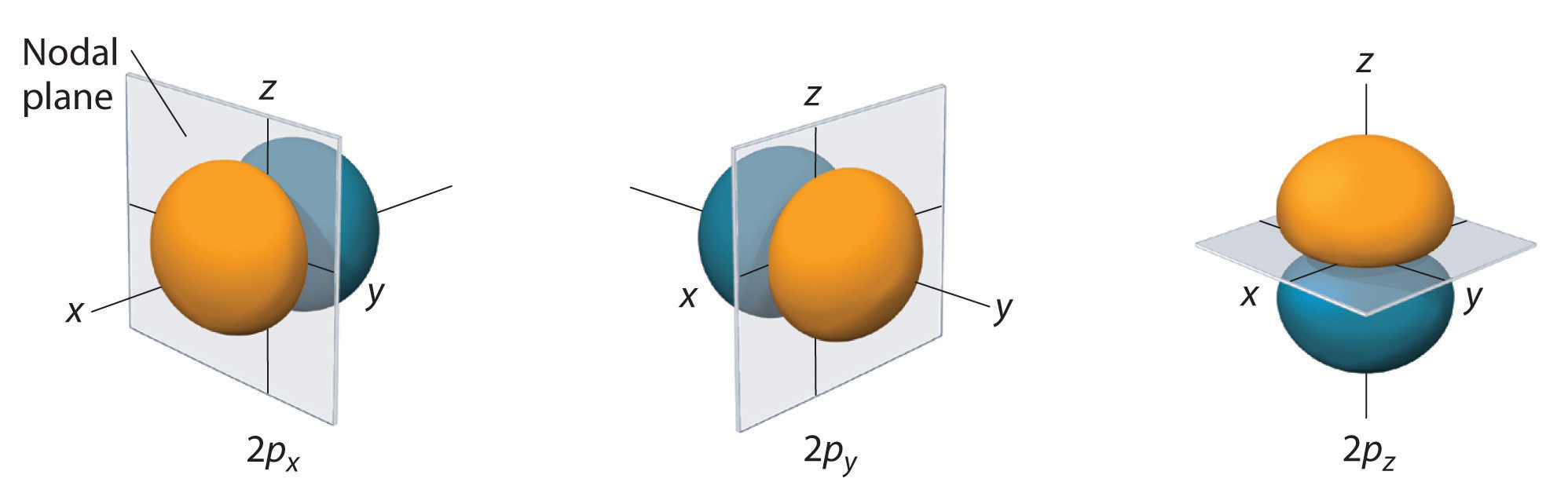
Przedstawione powierzchnie obejmują 90% całkowitego prawdopodobieństwa elektronu na orbitalach 2px, 2py i 2pz. Każdy orbital jest zorientowany wzdłuż osi oznaczonej indeksem, a płaszczyzna węzłowa, która jest prostopadła do tej osi przecina każdy orbital 2p. Faza funkcji falowej jest dodatnia (pomarańczowa) w obszarze przestrzeni, w którym x, y, o, z jest dodatnia i ujemna (niebieska), w którym x, y, o, z jest ujemna. Podobnie jak w przypadku orbitali s, rozmiar i złożoność orbitali p w każdym atomie rośnie wraz ze wzrostem głównej liczby kwantowej n. Kształty 90% powierzchni prawdopodobieństwa orbitali 3p, 4p i wyżejenergetycznych orbitali p są jednak zasadniczo takie same jak te pokazane na rysunku
Orbitale d (l=2)
Powłoki z l = 2 mają pięć orbitali d; pierwsza główna powłoka, która ma podpowłokę d odpowiada n = 3. Pięć orbitali d ma wartości ml -2, -1, 0, +1, i +2.
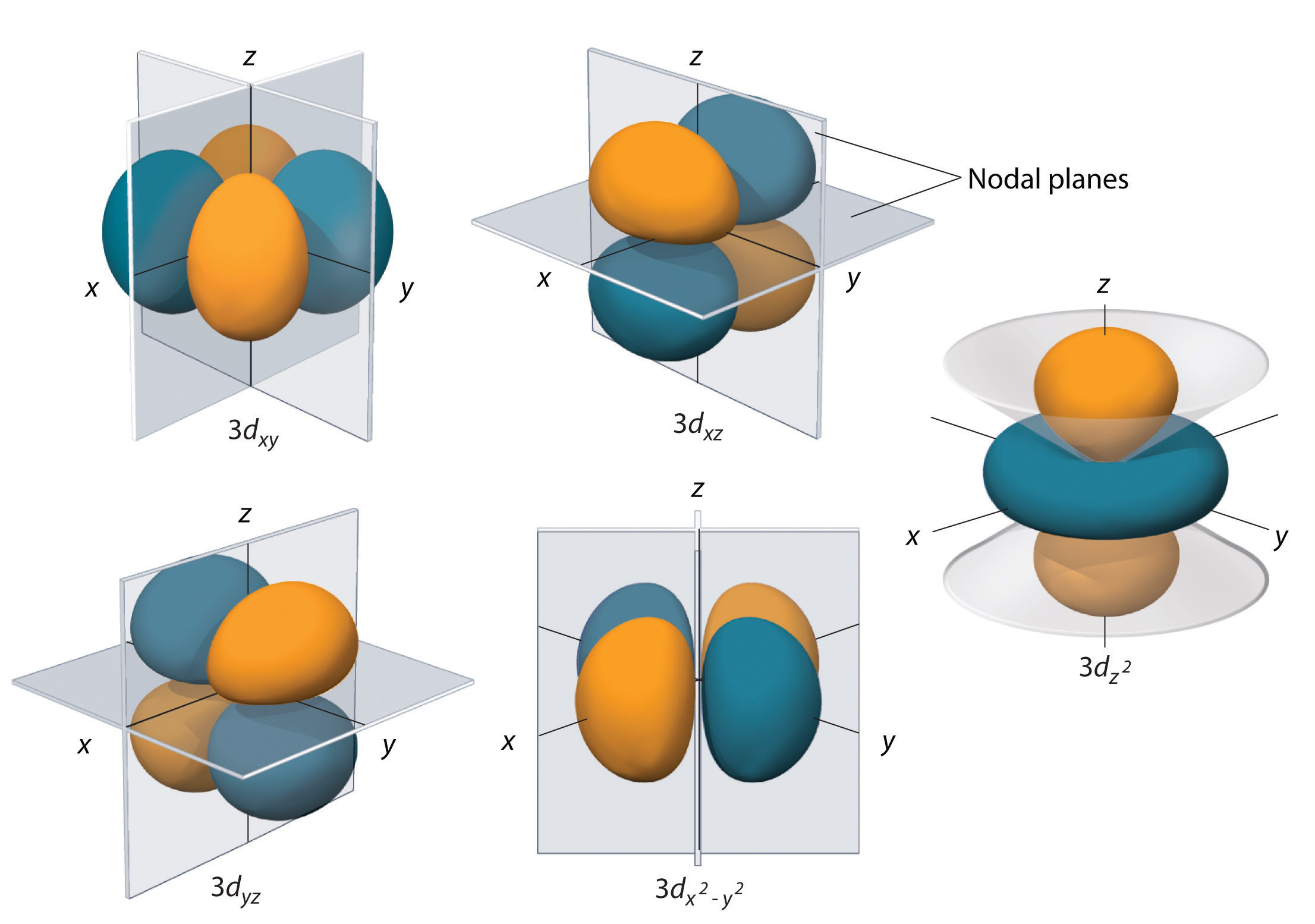
Orbitale 3d wodoru, pokazane na rysunku, mają bardziej złożone kształty niż orbitale 2p. Wszystkie pięć orbitali 3d zawiera dwie powierzchnie węzłowe, w porównaniu do jednej powierzchni węzłowej każdego orbitalu p i zero powierzchni węzłowej każdego orbitalu s. W trzech z orbitali d, płaty gęstości elektronowej są zorientowane pomiędzy płaszczyznami x i y, x i z, oraz y i z; orbitale te są określane jako orbitale \(3d_{xy}\), \(3d_{xz}\), i \(3d_{yz}\), odpowiednio. Czwarty orbital d ma płatki leżące wzdłuż osi x i y; jest to orbital \(3d_{x^2-y^2}). Piąty orbital 3d, zwany orbitalem 3d_{z^2}}, ma wyjątkowy kształt: wygląda jak orbital 2p_z połączony z dodatkowym pączkiem prawdopodobieństwa elektronowego leżącym w płaszczyźnie xy. Pomimo swojego osobliwego kształtu, orbital 3d_{z^2}} jest matematycznie równoważny innym orbitalom i ma taką samą energię. W przeciwieństwie do orbitali p, faza funkcji falowej dla orbitali d jest taka sama dla przeciwległych par płatów. Jak pokazano na rysunku faza funkcji falowej jest dodatnia dla dwóch płatów orbitalu d leżących wzdłuż osi z, natomiast faza funkcji falowej jest ujemna dla pączka gęstości elektronów w płaszczyźnie xy. Podobnie jak w przypadku orbitali s i p, wraz ze wzrostem n zwiększa się rozmiar orbitali d, ale ogólne kształty pozostają podobne do tych przedstawionych na rysunku
f Orbitale (l=3)
Pierwotne powłoki o n = 4 mogą mieć podpowłoki o l = 3 i wartościach ml -3, -2, -1, 0, +1, +2, i +3. Te podpowłoki składać się z siedem f orbitali. Każdy orbital f ma trzy powierzchnie węzłowe, więc ich kształty są złożone. Ponieważ orbitale f nie są szczególnie ważne dla naszych celów, nie omawiamy ich dalej, a orbitale z wysokimi wartościami l nie są w ogóle omawiane.
Energie orbitalne
Ale omówiliśmy kształty orbitali, powiedzieliśmy niewiele o ich energiach porównawczych. Rozpoczynamy naszą dyskusję o energiach orbitali rozważając atomy lub jony z tylko jednym elektronem (takie jak H o He+).
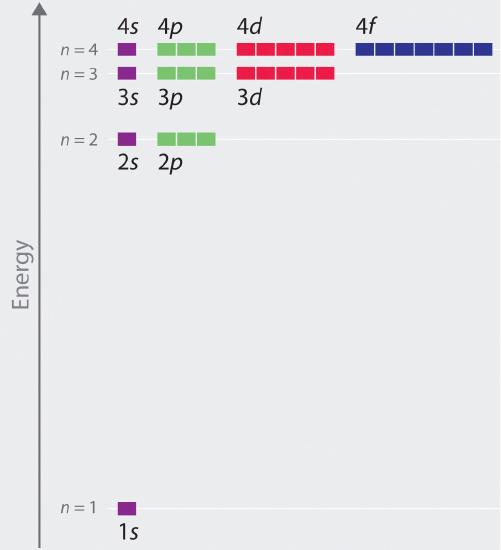
Względne energie orbitali atomowych z n ≤ 4 dla atomu wodoru są przedstawione na Rysunku; zauważ, że energie orbitali zależą tylko od głównej liczby kwantowej n. W konsekwencji, energie orbitali 2s i 2p wodoru są takie same; energie orbitali 3s, 3p i 3d są takie same; i tak dalej. Mechanika kwantowa przewiduje, że w atomie wodoru wszystkie orbitale o tej samej wartości n (np. trzy orbitale 2p) są zdegenerowane, co oznacza, że mają taką samą energię. Energie orbitali otrzymane dla wodoru za pomocą mechaniki kwantowej są dokładnie takie same jak dozwolone energie obliczone przez Bohra. W przeciwieństwie jednak do modelu Bohra, który dopuszczał tylko jeden orbital na każdym poziomie energetycznym, mechanika kwantowa przewiduje istnienie 4 orbitali o różnym rozkładzie gęstości elektronowej w powłoce głównej n = 2 (jeden orbital 2s i trzy 2p), 9 w powłoce głównej n = 3 i 16 w powłoce głównej n = 4.Różne wartości l i ml dla poszczególnych orbitali w danej powłoce głównej nie są istotne dla zrozumienia widm emisyjnych i absorpcyjnych atomu wodoru w większości warunków, ale wyjaśniają rozszczepienie głównych linii, które są obserwowane, gdy atomy wodoru są umieszczone w polu magnetycznym. Rysunek pokazuje, że poziomy energetyczne zbliżają się do siebie wraz ze wzrostem wartości n, co jest oczekiwane ze względu na zależność energii orbitalnych od 1/n2.
Energie orbitali w każdym gatunku z jednym elektronem mogą być obliczone przez mini odmianę równania Bohra, które może być rozszerzone na inne gatunki jednoelektronowe przez uwzględnienie ładunku jądra (liczby protonów w jądrze):
Ogólnie rzecz biorąc, zarówno energia jak i promień maleją wraz ze wzrostem ładunku jądra. Tak więc najbardziej stabilne orbitale (te o najniższej energii) to te najbliżej jądra. Na przykład, w stanie podstawowym atomu wodoru, pojedynczy elektron znajduje się na orbitalu 1s, podczas gdy w pierwszym stanie wzbudzonym, atom zaabsorbował energię i elektron został przeniesiony na jeden z orbitali n = 2. W jonach z pojedynczym elektronem energia danego orbitalu zależy tylko od n, a wszystkie podpowłoki w obrębie powłoki głównej, takie jak orbitale \(p_x\), \(p_y\) i \(p_z\) są zdegenerowane.
Podsumowanie
Chemicznie ważne typy orbitali atomowych odpowiadają wartościom \(\ell = 0\), \(1\), \(2\) i \(3\). Orbitale o wartości ≥ 0 są orbitalami s i są sferycznie symetryczne, z największym prawdopodobieństwem znalezienia elektronu występującego przy jądrze. Wszystkie orbitale o wartościach \(n > 1\) i \(ell = 0\) zawierają o jeden węzeł więcej. Orbitale z \ell = 1\) są orbitalami p i zawierają płaszczyznę węzłową obejmującą jądro, co daje kształt hantli. Orbitale z \(\ell = 2\) są orbitalami d i mają bardziej złożone kształty z co najmniej dwoma powierzchniami węzłowymi. Orbitale z ˆ = 3 ˆ są orbitalami f, które są jeszcze bardziej złożone.
Ponieważ jego średnia odległość od jądra określa energię elektronu, każdy orbital atomowy z danym zestawem liczb kwantowych ma szczególną energię z nim związaną, energię orbitalną.
W atomach o tylko jednym elektronie, wszystkie orbitale o tej samej wartości liczby kwantowej mają tę samą energię (są zdegenerowane), a energie powłok głównych rosną płynnie wraz ze wzrostem liczby kwantowej. Atom jonu z elektronem(ami) na orbitalu(ach) o najniższej energii jest w stanie podstawowym, natomiast atom jonu, w którym jeden elektron(y) więcej zajmuje orbitale o wyższej energii, jest w stanie wzbudzonym.
Współautorzy i przypisy
-
Zmodyfikowane przez Joshua Halpern (Howard University)
.