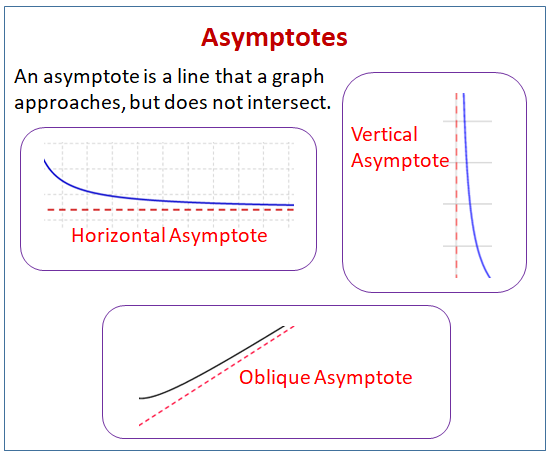
Asymptota to linia, do której zbliża się wykres, ale jej nie przecina.
W tej lekcji, dowiemy się, jak znaleźć pionowe asymptoty, poziome asymptoty i skośne asymptoty funkcji racjonalnych.
Powiązane tematy:
Więcej lekcji na temat rachunku

Następujący diagram pokazuje różne rodzaje asymptot: asymptoty poziome, asymptoty pionowe i asymptoty skośne. Przewiń stronę w dół, aby znaleźć więcej przykładów i rozwiązań, jak znaleźć asymptoty.

Jak wyznaczyć asymptotę pionową?

Metoda 1: Użyj definicji asymptoty pionowej

Prostą x = a nazywamy asymptotę pionową krzywej y = f(x), jeśli przynajmniej jedno z poniższych stwierdzeń jest prawdziwe.

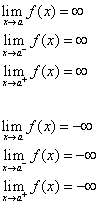
Metoda 2:

Dla funkcji racjonalnych asymptoty pionowe są liniami pionowymi, które odpowiadają zerom mianownika.
Dana jest funkcja racjonalna, f(x)

Krok 1: Napisz f(x) w postaci zredukowanej

Krok 2: jeśli x – c jest współczynnikiem w mianowniku to x = c jest asymptotą pionową.

Przykład:

Znajdź asymptoty pionowe funkcji

Rozwiązanie:

Metoda 1: Skorzystaj z definicji Asymptoty pionowej.

Jeśli x jest bliskie 3, ale większe od 3, to mianownik x – 3 jest małą liczbą dodatnią, a 2x jest bliskie 8. Zatem jest dużą liczbą dodatnią.

Intuicyjnie widzimy, że

Podobnie, jeśli x jest bliskie 3, ale mniejsze od 3, to x – 3 jest małą liczbą ujemną, a 2x jest bliskie 8. Zatem jest dużą liczbą ujemną.

Linia x = 3 jest asymptotą pionową.

Metoda 2:

Krok 1: f(x) jest już w postaci zredukowanej.

Krok 2: Mianownik wynosi x – 3, a więc asymptota pionowa znajduje się w punkcie x = 3.

Znajdowanie pionowych asymptot funkcji wymiernych

Na co zwrócić uwagę, aby znaleźć pionowe asymptoty funkcji wymiernych.

• Pokaż rozwiązania krok po kroku

Pionowe asymptoty funkcji wymiernych: Quick Way to Find Them

Przykład znajdowania pionowych asymptot funkcji racjonalnych.

• Pokaż rozwiązania krok po kroku

Jak znaleźć pionowe asymptoty funkcji racjonalnych

• Pokaż rozwiązania krok po kroku

Jak wyznaczyć asymptotę poziomą?

Metoda 1: Skorzystaj z definicji Asymptoty poziomej

Prostą y = L nazywamy asymptotę poziomą krzywej y = f(x), jeśli albo

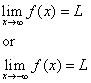
Metoda 2:

Dla funkcji racjonalnej, f(x)

Jeśli stopień x w liczniku jest mniejszy niż stopień x w mianowniku to y = 0 jest asymptotą poziomą.

Jeżeli stopień x w liczniku jest równy stopniowi x w mianowniku to y = c, gdzie c otrzymujemy przez dzielenie współczynników wiodących.

Przykład:

Znajdź asymptoty poziome i pionowe funkcji.

Rozwiązanie:

Metoda 1:

Podziel oba liczniki i mianownik przez x.

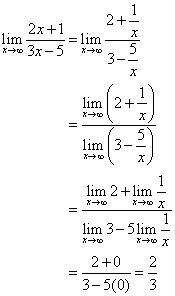
Prosta jest asymptotą poziomą.

Metoda 2:

Stopień x w liczniku jest równy stopniowi x w mianowniku.

Dzieląc wiodące współczynniki otrzymujemy

Linia jest asymptotą poziomą.

Shortcut to Find Horizontal Asymptotes of Rational Functions

Kilka sztuczek, które bardzo ułatwiają znajdowanie asymptot poziomych funkcji racjonalnych

• Pokaż rozwiązania krok po kroku

W tym filmie przedstawimy podstawowy przegląd asymptot poziomych. Określimy, czy dane funkcje racjonalne mają asymptoty poziome i czym one są.

• Pokaż rozwiązania krok po kroku

W tym filmie omówimy bardziej szczegółowo zasady asymptot poziomych.

• Pokaż rozwiązania krok po kroku

Asymptota skośna lub asymptota ukośna

Niektóre krzywe mają asymptoty ukośne, czyli ani poziome, ani pionowe.

Jeśli to prosta y = mx + b jest nazywana asymptotą skośną, ponieważ odległości pionowe między krzywą y = f(x) a prostą y = mx + b zbliżają się do 0.

Dla funkcji racjonalnych asymptoty skośne występują, gdy stopień licznika jest o jeden większy od stopnia mianownika. W takim przypadku równanie asymptoty skośnej można znaleźć przez długie dzielenie.

Przykład:

Znajdź asymptoty funkcji

Rozwiązanie:

Ponieważ mianownik x2 + 1 nigdy nie jest równy 0, nie ma asymptoty pionowej.

Ponieważ stopień x w liczniku jest większy od stopnia x w mianowniku nie ma asymptoty poziomej.

Ponieważ stopień x w liczniku jest o jeden większy od stopnia x w mianowniku możemy zastosować długie dzielenie, aby otrzymać asymptotę skośną.

Więc, linia y = x jest asymptotą skośną.

Znajdowanie asymptot skośnych funkcji rzeczywistych

Ten film opisuje kiedy funkcja rzeczywista ma asymptotę skośną, krótko opisuje czym jest asymptota skośna, a następnie podaje dwa przykłady.

• Pokaż rozwiązania krok po kroku

Znajdowanie asymptot funkcji rzeczywistej (pionowe, poziome i skośne)

Ten film pokazuje jak znaleźć pionowe asymptoty i skośne asymptoty funkcji rzeczywistej.

• Pokaż rozwiązania krok po kroku

Znajdowanie wszystkich asymptot funkcji (pionowych, poziomych, skośnych)

Przyglądamy się funkcji i znajdujemy asymptotę pionową, a także stwierdzamy, że nie ma asymptot poziomych, ale istnieje asymptota skośna. Następnie używamy długiego podziału, aby znaleźć skośną asymptotę.

• Pokaż rozwiązania krok po kroku

Wypróbuj darmowy kalkulator matematyczny i narzędzie do rozwiązywania zadań poniżej, aby ćwiczyć różne tematy matematyczne. Wypróbuj podane przykłady lub wpisz swój własny problem i sprawdź swoją odpowiedź, korzystając z objaśnień krok po kroku.