To co następuje to moje podejście do niektórych problemów matematycznych z rzekomo „common core math” lub „nowej matematyki”, które krążyły w internecie. Czuję, że pokazują nam źle ukierunkowaną implementację CCS.

Zachowaj w umyśle, nie wszystko co widzisz w książkach matematycznych lub w internecie jest poprawnie zrobione w oparciu o CCS. W niektórych przykładach, które widzisz, wygląda na to, że ludzie wyrzucają zdrowy rozsądek przy rozwiązywaniu problemów matematycznych, aby odnieść się do standardów Common Core!

Nie jestem zaskoczony, że wdrożenie skończyło się „spartaczone” w niektórych miejscach. CCS są taką zmianą dla większości nauczycieli, że potrzebują dużo wsparcia i reedukacji zanim zostaną zobowiązani do nauczania ich.

Zawsze myślałem, że GŁÓWNYM problemem stojącym przed edukacją matematyczną w klasach podstawowych w szkołach publicznych jest to, że wielu nauczycieli klas podstawowych nie rozumie matematyki na tyle, by być w stanie uczyć jej poprawnie nawet na poziomie podstawowym. Na przykład, wielu z nich nie rozumie pojęć, dlaczego i gdzie są algorytmy, których uczą. Nie jest to ich wina – problem tkwi w tym, czego uczono ich w trakcie kształcenia nauczycieli i w ich własnej szkole.

Nawet sam dokument standardów jest miejscami nieco trudny do zrozumienia. Czytanie go wymaga trochę myślenia. Chciałbym, żeby ktoś wydał broszurę, która wyjaśnia standardy prostym językiem i z licznymi przykładami.

Złe przykłady „common core” lub „nowej matematyki”

Przykład 1

Ostatnio widziałem na Facebooku obraz strategii odejmowania, który twierdził, że pochodzi z podręcznika matematyki dla 1 klasy i jest „matematyką Common Core.”

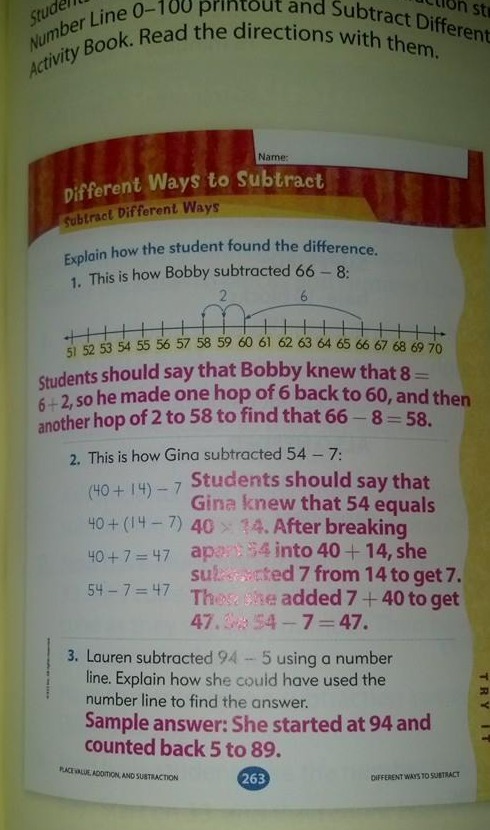
Myślę, że metoda 2 jest zbyt trudna dla 1 klasy, i zostawiłbym nawet metodę 1 dla 2 klasy.

Jednakże, ta książka nie wydaje się nawet wyrównywać z normami Common Core. Standardy dla 1 klasy po prostu nie zawierają tego rodzaju problemów z odejmowaniem!

To jest to co znajdziemy w standardach:

Dodawaj i odejmuj w zakresie 20.
1.OA.5
Odnoszenie liczenia do dodawania i odejmowania (np. licząc na 2, aby dodać 2).
1.OA.6.
Dodawanie i odejmowanie w zakresie 20, wykazując biegłość w dodawaniu i odejmowaniu w zakresie 10. Używa strategii takich jak liczenie dalej; tworzenie dziesięciu (np., 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14); rozkładanie liczby prowadzącej do dziesięciu (np., 13 – 4 = 13 – 3 – 1 = 10 – 1 = 9); używanie relacji pomiędzy dodawaniem i odejmowaniem (np., wiedząc, że 8 + 4 = 12, wiemy, że 12 – 8= 4); i tworzenie równoważnych, ale łatwiejszych lub znanych sum (np, dodawanie 6 +7 przez tworzenie znanego odpowiednika 6 + 6 + 1 = 12 + 1 = 13).

Przykład z podręcznika wydaje się chcieć odnieść się do 1.OA.6 powyżej, ale to jest wyraźnie dla dodawania i odejmowania w granicach 20, nie z większymi liczbami.

Później w standardach 1 klasy widzimy dwa standardy, które mają do czynienia z odejmowaniem liczb dwucyfrowych (w granicach 100):

1.NBT.5.
Dając liczbę dwucyfrową, mentalnie znaleźć 10 więcej lub 10 mniej niż liczba, bez konieczności liczenia; wyjaśnić zastosowane rozumowanie.
1.NBT.6.
Odejmowanie wielokrotności liczby 10 w zakresie 10-90 od wielokrotności liczby 10 w zakresie 10-90 (dodatnie lub zerowe różnice), używając konkretnych modeli lub rysunków i strategii opartych na wartości miejsc, właściwościach działań i/lub związku pomiędzy dodawaniem i odejmowaniem; odniesienie strategii do pisemnej metody i wyjaśnienie użytego rozumowania.
Uwaga Marii: oznacza to odejmowanie takie jak 34 – 20 lub 89 – 60.

Ale żadne z nich nie obejmuje odejmowania takiego jak 54 – 7 lub 82 – 6. Te są w 2 klasie:

2.NBT.5
Płynnie dodaje i odejmuje w zakresie 100 używając strategii opartych na wartości miejsca, właściwości operacji, i / lub związek między dodawaniem i odejmowaniem.

Zauważ, że standard 2 klasy nie określa JAK odejmować (czy używasz strategii matematyki mentalnej czy piszesz liczby pod sobą i pożyczasz/grupujesz).

Przykład 2

Z Houghton Mifflin, podobno:

Juanita chce dać torebki naklejek swoim przyjaciołom. Chce dać każdemu przyjacielowi taką samą liczbę naklejek. Nie jest pewna, czy potrzebuje 4 czy 6 worków naklejek. Ile naklejek mogłaby kupić, żeby nie zostały żadne naklejki?

Problem z naklejkami ma związek z pojęciem najmniejszej wspólnej wielokrotności (LCM). (Odpowiedź brzmi: powinna kupić 12, 24, 36, lub jakąkolwiek inną wielokrotność 12 naklejek, ponieważ wtedy może je podzielić albo na 4 woreczki, albo na 6 woreczków.)

Zapewne, problem jest BARDZO niejasny i źle sformułowany. Wydaje mi się, że książeczka, w której to się pojawia, jest po prostu niezredagowana. Nie jest to wina samych standardów. Zgadzam się z Bartem Goddardem na Math Forum. To jest symptom ślepego pędu do tworzenia „realnych” problemów z historii, które w końcu stają się bezsensowne.

Z dokumentu PDF, w którym to się pojawia, wnioskuję, że problem jest dla czwartej klasy, ponieważ wszystkie inne problemy słowne w książeczce pasują do standardów dla czwartej klasy (czynniki, liczby pierwsze). Ale CCS nawet nie uwzględnia najmniejszej wielokrotności w standardach dla 4 klasy (jest w 6)!!! Coś poszło naprawdę nie tak z tym problemem słownym.

Przykład 3

Powtarzam, podobno z Houghton Mifflin dla 1 klasy. To pasuje do standardu, który już przytoczyłem powyżej:

Add and subtract within 20.
1.OA.6.
Add and subtract within 20, demonstrating fluency for addition andsubtraction within 10. Używa strategii takich jak liczenie dalej; tworzenie dziesiątki (np. 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14); rozkładanie liczby prowadzącej do dziesiątki (np. 13 – 4 = 13 – 3 – 1 = 10 – 1 = 9); używanie relacji pomiędzy dodawaniem i odejmowaniem (np, wiedząc, że 8 + 4 = 12, jeden wie 12 – 8= 4); i tworzenie równoważnych, ale łatwiejsze lub znane sumy (np. dodawanie 6 +7 tworząc znany odpowiednik 6 + 6 + 1 = 12 + 1 = 13).

Now, po pierwsze, strategia „podejmowania dziesięć” ma do czynienia z ADDITION, nie odejmowanie. W odejmowaniu nazywa się to „rozkładaniem liczby prowadzącej do dziesiątki”. Więc instrukcja powinna mówić: „Która pokazuje sposób rozkładania liczby prowadzący do dziesiątki?”. Czuję, że to kompletny NONSENS wymagać od uczniów 1 klasy, aby znać taką terminologię.

Ale jest jeszcze jeden problem tutaj. Jeśli rzeczywiście przeczytasz wszystkie standardy, zauważysz, że w kilku innych miejscach prosi się uczniów o wyjaśnienie użytego rozumowania lub o powiązanie pewnej metody wizualnej ze strategią, ale NIE w tym standardzie!

Jak widzę ten standard, nauczyciele powinni uczyć różnych strategii wymienionych w tym standardzie, a następnie dać uczniom proste problemy z dodawaniem i odejmowaniem w zakresie 20, takie jak 15 – 8 i 10 – 6. Nie widzę, aby ta norma wymagała od uczniów rozpoznawania, czy dany model wizualny pasuje do danej strategii.

Ponownie, wygląda na to, że autor wyrzuca zdrowy rozsądek… i nie rozumie standardów.

Przykład 4

Przykład poniżej jest bardzo słabo sformułowany, ale KONCEPCJA stojąca za nim jest bardzo dobra i znajduje się również w Math Mammoth. Mogę zatem domyślić się, o co im chodzi.

Widzisz pięć kwadratów. Niektóre z nich pokoloruj na niebiesko, a pozostałe na czerwono. To jest jasne.

Potem pokoloruj kwadraty w „więzi liczbowej” w ten sam sposób. Więź liczbowa idzie do tych trzech kółek. Dziecko, które było obecne w lekcji, gdzie nauczyciel uczy więzi liczbowych, ma nadzieję, że wie, co to znaczy. Jest to taka sama koncepcja jak rodzina faktów… górna liczba jest sumą lub sumą całkowitą (5), a liczby, które idą do dolnych kółek odpowiadają temu, ile pokolorowałeś na niebiesko, a ile na czerwono, w tym przypadku 1 i 4.

Wtedy myślę, że ukryci partnerzy są również 1 i 4. Pokaż 1 i 4 palce osobie dorosłej. Na koniec pokoloruj palce 1 i 4 na obrazku (a nie własne palce, jak to brzmi).

W mojej opinii część o palcach jest superflous i mylące. Jednakże, koncepcja wiązań liczbowych jest o wiele starsza niż CCS. Więzy liczbowe nie są wspomniane w CCS, chociaż wiążą się z tym standardem:

1.OA.4
Uznaj odejmowanie jako problem nieznanego-dodawania. Na przykład, odjąć 10 – 8 przez znalezienie liczby, która daje 10 po dodaniu do 8.

i z tym

1.OA.6.
Dodaj i odejmij w ciągu 20, demonstrując biegłość dla dodawania i odejmowania w ciągu 10.

Nie wiem, dlaczego ten arkusz wiązania liczb jest podany jako przykład Common Core Math. Byłoby to o wiele lepiej zatytułowane jako przykład źle sformułowanego arkusza matematycznego, który mógłby nawet pochodzić z okresu przed Common Core (i jest po prostu ponownie wykorzystany w tym konkretnym programie nauczania)… ponieważ, jak już powiedziałem, wiązania liczbowe NIE są wspomniane w CCS.

Czym Common Core Math Standards nie są

1. Nie są one „nową matematyką”. W porównaniu z wieloma programami nauczania matematyki stosowanymi w latach 2000, które podkreślały nietradycyjne algorytmy, CCS jest wyraźnym ruchem w kierunku tradycyjnych algorytmów i zapamiętywania. Sprawdź te konkretne standardy:
   

   2.OA.2
   Płynnie dodawaj i odejmuj w zakresie 20 używając strategii umysłowych. Do końca klasy 2, znać z pamięci wszystkie sumy dwóch liczb jednocyfrowych.
   Uwaga Marii: to są twoje podstawowe fakty dodawania, takie jak 7 + 7 lub 5 + 4.

   3.OA.7
   Płynnie mnożyć i dzielić w zakresie 100, używając strategii takich jak związek pomiędzy mnożeniem i dzieleniem (np. wiedząc, że 8 × 5 = 40, wiemy, że 40 ÷ 5 = 8) lub właściwości działań. Do końca klasy 3, znać z pamięci wszystkie iloczyny dwóch liczb jednocyfrowych.
   Uwaga Marii: oznacza to tabliczkę mnożenia i podstawowe fakty dotyczące dzielenia.

   4.NBT.4
   Płynnie dodawać i odejmować wielocyfrowe liczby całkowite stosując standardowy algorytm.

   5.NBT.5
   Płynnie mnożyć wielocyfrowe liczby całkowite stosując standardowy algorytm.
   Uwaga Marii: nie oznacza to, że uczniowie mnożą wielocyfrowe liczby całkowite tylko w 5 klasie; jest to również badane w 3 i 4 klasie.

2. Standardy nie narzucają nauczycielom i uczniom dziwnych strategii czy modeli wizualnych. Wiele standardów pozostawia to w gestii nauczycieli i uczniów. Na przykład:
   

   2.NBT.5
   Płynnie dodaje i odejmuje w zakresie 100 używając strategii opartych na wartościach miejscowych, własnościach działań, i/lub związku między dodawaniem i odejmowaniem.

   Zauważ „i/lub” w powyższym zdaniu. Oznacza to, że nauczyciele i uczniowie NIE są ograniczeni do stosowania żadnych konkretnych strategii, ani nie są zmuszeni do stosowania kilku strategii. Tradycyjny algorytm „pożyczania” jest strategią opartą na wartości miejsc, więc jest on włączony właśnie tutaj, w 2.NBT.5.

   2.NBT.9
   Wyjaśnić dlaczego strategie dodawania i odejmowania działają, używając wartości miejsca i własności działań. Wyjaśnienia mogą być poparte rysunkami lub obiektami.

   To mówi „mogą być poparte rysunkami”, ale nie zmusza cię do tego, ani nie ogranicza cię do używania konkretnego modelu wizualnego lub typu rysunku.

   3.OA.3
   Użycie mnożenia i dzielenia w zakresie 100 do rozwiązywania problemów słownych w sytuacjach dotyczących równych grup, tablic i wielkości pomiarowych, np. poprzez użycie rysunków i równań z symbolem nieznanej liczby do przedstawienia problemu.

   Uczeń nie MUSI używać rysunku. To jest tylko wspomniane jako możliwość.

   4.NBT.5
   Mnoży liczbę całkowitą do czterech cyfr przez jednocyfrową liczbę całkowitą i mnoży dwie dwucyfrowe liczby, używając strategii opartych na wartości miejsc i właściwościach działań. Ilustrowanie i wyjaśnianie obliczeń przy użyciu równań, tablic prostokątnych, i/lub modeli.

   Uwaga na „i/lub”. Zilustruj obliczenia, ale wystarczy zilustrować je za pomocą równań. Nie MUSISZ ilustrować tego używając tablic.

   To powiedziawszy, niektóre standardy wspominają o konkretnym modelu wizualnym, takim jak linia liczbowa lub model prostokątnego obszaru, ale jest to mniej powszechne niż dawanie wyboru jak w powyższych standardach.

Matematyka pojęciowa

Są pewne standardy, które dotyczą pojęciowej strony matematyki, której nauczyciele szkół podstawowych mogą nie zrozumieć, jeśli nie zostaną nauczeni, co one oznaczają; na przykład:

5. NF.7b
Interpretowanie dzielenia liczby całkowitej przez ułamek jednostkowy i obliczanie takich ilorazów. Na przykład, stworzyć kontekst fabularny dla 4 ÷ (1/5) i użyć wizualnego modelu ułamka, aby pokazać iloraz. Użyj relacji między mnożeniem i dzieleniem, aby wyjaśnić, że 4 ÷ (1/5) = 20, ponieważ 20 × (1/5) = 4.

Jednym z takich problemów może być: ile kawałków o długości 1/5 stopy można wyciąć z kawałka materiału o długości 4 stóp? Model wizualny mógłby pokazywać 4 całości, podzielone na części piąte. Możemy wtedy policzyć, że 4 całości mają w sumie 20 piątych części.

5.NF.4b
Znajdujemy pole prostokąta o ułamkowych długościach boków poprzez pokrycie go kwadratami jednostkowymi o odpowiednich długościach boków ułamka jednostkowego i pokazujemy, że pole jest takie samo, jakie otrzymalibyśmy mnożąc długości boków. Mnożymy ułamkowe długości boków, aby znaleźć pola prostokątów, i przedstawiamy iloczyny ułamkowe jako pola prostokątów.

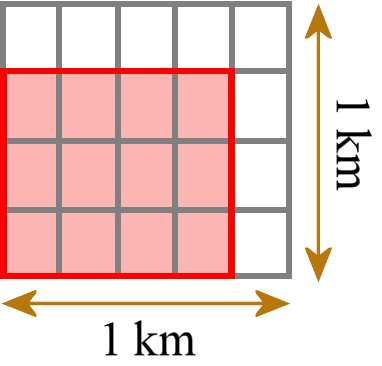To oznacza na przykład prostokąt o długościach boków 3/4 km i 4/5 km. Następnie wykładamy go małymi prostokątami jednostkowymi (nie kwadratami jednostkowymi; tutaj norma sama stosuje błędną terminologię), z których każdy ma bok o długości 1/4 km i 1/5 km.

Możemy policzyć, ile małych płytek potrzebujemy. Potrzebujemy 12 takich płytek. Każdy kafelek ma powierzchnię 1/20 km2, więc łączna powierzchnia wynosi 12/20 km2. Następnie sprawdzamy i porównujemy, że otrzymujemy taką samą odpowiedź, jak gdybyśmy pomnożyli dwie długości boków używając zwykłego mnożenia ułamków (3/4 km × 4/5 km = 12/20 km2).

Zawsze miałem tego typu problemy w moich książkach – nawet zanim pojawił się CCS.

Niektórzy argumentują, że dzieci nie potrzebują takiego zrozumienia pojęciowego lub że jest to zbyt trudne. Osobiście, nie zgadzam się z tym. Zawsze (również przed CCS) dążyłem do wyjaśnienia pojęć arytmetyki ułamkowej tak, aby uczniowie nie skończyli „ślepo podążając za regułami”, zdolni do obliczania ułamków tylko wtedy, gdy dobrze zapamiętają regułę. Zawsze kładłem nacisk na zrozumienie pojęciowe w matematyce (jak moi czytelnicy wiedzą!).

Mam jednak nadzieję, że widzicie jak niektóre z tych rzeczy mogą być nieznane nauczycielom szkolnym i rodzicom, i dlatego nie jest dziwne, że przestrzeganie Common Core Standards jest dla nich trudne.

Mam nadzieję, że Math Mammoth Light Blue Series i jednostki, które sprzedaję w moich sklepach Teachers Pay Teachers i Teachers’ Notebook mogą pomóc tym nauczycielom & rodzicom, którzy potrzebują Common Core wyrównane materiały. I jak powiedziałem, reszta z was może być pewny siebie w ich użyciu, jak również. Nie zawierają one żadnych „dziwnych” czy bezsensownych pojęć matematycznych, ale jak zawsze są po prostu oparte na solidnych podstawach nauczania pojęć matematycznych wraz z procedurami.

Przez Maria Miller