Tożsamość Eulera wydaje się zaskakująca:

Wynika z bardziej ogólnego wzoru:

Yowza — odnosimy urojony wykładnik do sinusa i cosinusa! I w jakiś sposób wstawienie pi daje -1? Czy to w ogóle może być intuicyjne?

Nie według matematyka z 1800 roku Benjamina Peirce’a:

To jest absolutnie paradoksalne; nie możemy tego zrozumieć i nie wiemy, co to znaczy, ale udowodniliśmy to i dlatego wiemy, że to musi być prawda.

Argh, takie podejście sprawia, że krew mi się gotuje! Formuły nie są magicznymi zaklęciami, które należy zapamiętać: musimy, musimy, musimy znaleźć wgląd. Oto moje:

Wzór Eulera opisuje dwa równoważne sposoby poruszania się po okręgu.

To wszystko? To oszałamiające równanie dotyczy kręcenia się w kółko? Tak — i możemy je zrozumieć, opierając się na kilku analogiach:

• Zaczynając od liczby 1, zobacz mnożenie jako transformację, która zmienia liczbę: $1 ^cdot e^{i ^pi}$
• Regularny wzrost wykładniczy stale zwiększa 1 o pewną stopę przez pewien okres czasu; urojony wzrost wykładniczy stale obraca 1 przez pewien okres czasu
• Rośnięcie przez „pi” jednostek czasu oznacza obracanie pi radianów wokół koła
• Dlatego $e^{i \i}$ oznacza rozpoczęcie od 1 i obracanie pi (w połowie drogi wokół koła), aby dostać się do -1

To jest widok wysokiego poziomu, zanurzmy się w szczegółach. Przy okazji, jeśli ktoś próbuje zaimponować ci $e^{i \i} = -1$, zapytaj go o i do i-tej potęgi. Jeśli nie potrafią tego przemyśleć, formuła Eulera wciąż jest dla nich magicznym zaklęciem.

Update: Podczas pisania pomyślałem, że wideo może pomóc wyjaśnić idee bardziej przejrzyście:

Understanding cos(x) + i * sin(x)

Znak równości jest przeciążony. Czasem mamy na myśli „ustaw jedną rzecz na drugą” (jak x = 3), a innym razem mamy na myśli „te dwie rzeczy opisują tę samą koncepcję” (jak $sqrt{-1} = i$).

Wzór Eulera jest tym drugim: daje dwa wzory, które wyjaśniają, jak poruszać się po okręgu. Jeśli zbadamy ruch po okręgu używając trygon, i przemieścimy się x radianów:

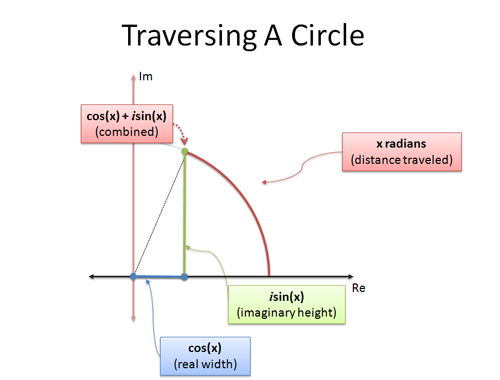
• cos(x) jest współrzędną x (odległość pozioma)
• sin(x) jest współrzędną y (odległość pionowa)

Stwierdzenie

jest sprytnym sposobem na zmiażdżenie współrzędnych x i y w jedną liczbę. Analogia „liczby zespolone są dwuwymiarowe” pomaga nam interpretować pojedynczą liczbę zespoloną jako położenie na okręgu.

Gdy ustawimy x na $pi$, podróżujemy $pi$ jednostek wzdłuż zewnętrznej części okręgu jednostkowego. Ponieważ całkowity obwód wynosi $2pi$, zwykłe stare $pi$ jest w połowie drogi, co stawia nas w punkcie -1.

Neato: Prawa strona wzoru Eulera ($cos(x) + i \sin(x)$) opisuje ruch po okręgu z liczbami urojonymi. Teraz dowiedzmy się, jak strona e równania to osiąga.

Czym jest wzrost urojonych?

Łączenie współrzędnych x i y w liczbę złożoną jest trudne, ale możliwe do wykonania. Ale co oznacza wykładnik urojonego?

Cofnijmy się trochę. Kiedy widzę $3^4$, myślę o tym w ten sposób:

• 3 jest wynikiem końcowym natychmiastowego wzrostu (używając e) w tempie ln(3). Innymi słowy: $3 = e^{ln(3)}$
• $3^4$ jest tym samym, co wzrost do 3, ale następnie rośnie przez 4x tak długo. Więc $3^4 = e^{ln(3) ^cdot 4} = 81$

Zamiast widzieć liczby same w sobie, możesz myśleć o nich jako o czymś, do czego e musiał „dorosnąć”. Liczby rzeczywiste, takie jak 3, dają stopę procentową ln(3) = 1.1, i to jest to, co e „zbiera”, gdy idzie, rosnąc nieprzerwanie.

Regularny wzrost jest prosty: utrzymuje „pchanie” liczby w tym samym, rzeczywistym kierunku, w którym szła. 3 × 3 popycha w pierwotnym kierunku, czyniąc ją 3 razy większą (9).

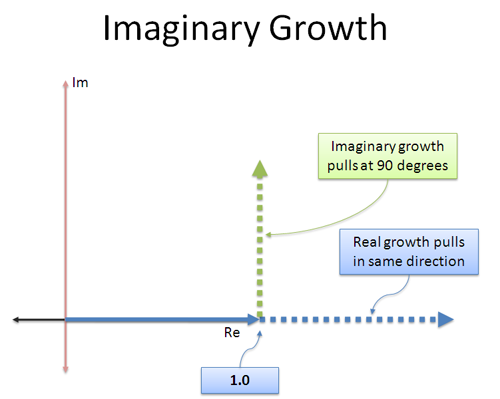
Wyobrażeniowy wzrost jest inny: „odsetki”, które zarabiamy są w innym kierunku! To jak silnik odrzutowy, który został przypięty z boku — zamiast iść do przodu, zaczynamy pchać pod kątem 90 stopni.

Zabawną rzeczą w stałym ortogonalnym (prostopadłym) pchaniu jest to, że nie przyspiesza cię ani nie zwalnia — ono cię obraca! Wzięcie dowolnej liczby i pomnożenie jej przez i nie zmieni jej wielkości, tylko kierunek, w którym wskazuje.

Intuicyjnie, oto jak widzę ciągłe wyimaginowane tempo wzrostu: „Kiedy rosnę, nie popychaj mnie do przodu lub do tyłu w kierunku, w którym już zmierzam. Obróć mnie zamiast tego.”

Ale Shouldn’t We Spin Faster and Faster?

Też się nad tym zastanawiałem. Regularny wzrost potęguje się w naszym pierwotnym kierunku, więc idziemy 1, 2, 4, 8, 16, mnożąc 2x za każdym razem i pozostając w liczbach rzeczywistych. Możemy rozważyć to $e^{ln(2)x}$, co oznacza natychmiastowy wzrost w tempie ln(2) przez „x” sekund.

I hej — gdyby nasze tempo wzrostu było dwa razy szybsze, 2ln(2) vs ln(2), wyglądałoby to tak samo, jak wzrost przez dwa razy dłuższy czas (2x vs x). Magia e pozwala nam zamienić tempo i czas; 2 sekundy przy ln(2) to taki sam wzrost jak 1 sekunda przy 2ln(2).

Teraz wyobraźmy sobie, że mamy jakieś czysto wyimaginowane tempo wzrostu (Ri), które obraca nas aż do osiągnięcia i, czyli 90 stopni w górę. Co się stanie, jeśli podwoimy to tempo do 2Ri, czy będziemy się obracać poza okręgiem?

Nie! Posiadanie tempa 2Ri oznacza, że po prostu obracamy się dwa razy szybciej, lub alternatywnie, obracamy się z prędkością R przez dwa razy dłużej, ale pozostajemy na okręgu. Obracanie się dwa razy dłużej oznacza, że jesteśmy teraz zwróceni o 180 stopni.

Odkąd zdamy sobie sprawę, że jakaś wykładnicza stopa wzrostu może nas zabrać z 1 do i, zwiększenie tej stopy po prostu bardziej nas kręci. Nigdy nie uciekniemy z koła.

Jednakże, jeśli nasza stopa wzrostu jest złożona (a+bi vs Ri), to część rzeczywista (a) będzie nas rozwijać jak zwykle, podczas gdy część urojona (bi) obraca nas. Ale nie popadajmy w fantazję: Wzór Eulera, $e^{ix}$, dotyczy czysto urojonego wzrostu, który utrzymuje nas na okręgu (więcej później).

A Quick Sanity Check

Podczas pisania musiałem wyjaśnić sobie kilka pytań:

Po co używać $e^x$, czy nie obracamy liczby 1?

e reprezentuje proces rozpoczynania od 1 i ciągłego wzrostu przy 100% odsetkach przez 1 jednostkę czasu.

Kiedy piszemy e, ujmujemy cały ten proces w jednej liczbie — e reprezentuje cały ten rigmarole ciągłego wzrostu. Więc tak naprawdę, $e^x$ mówi „zacznij od 1 i rośnij nieprzerwanie w 100% przez x sekund”, a zaczyna się od 1, tak jak chcemy.

Ale co robi i jako wykładnik?

Dla wykładnika regularnego, takiego jak $3^4$, pytamy:

• Jaka jest ukryta szybkość wzrostu? Rośniemy z 1 do 3 (podstawa wykładnika).
• Jak zmienimy tę stopę wzrostu? Skalujemy ją o 4x (potęga wykładnika).

Możemy przekonwertować nasz wzrost na format „e”: nasza stopa chwilowa to ln(3), a my zwiększamy ją do ln(3) * 4. Ponownie, potęga wykładnika (4) właśnie przeskalowała nasz wzrost.

Gdy górnym wykładnikiem jest i (jak w $3^i$), po prostu mnożymy naszą ukrytą stopę wzrostu przez i. Zamiast więc rosnąć w zwykłym, starym tempie ln(3), rośniemy w tempie ln(3) * i.

Górna część wykładnika modyfikuje ukrytą stopę wzrostu dolnej części.

The Nitty Gritty Details

Przyjrzyjrzyjrzyjmy się temu bliżej. Zapamiętaj definicję e:

Ta $frac{100%}{n}$ reprezentuje część odsetek, które zarobiliśmy w każdym mikroskopowym okresie. Założyliśmy, że stopa procentowa wynosi 100% w wymiarze rzeczywistym — ale co by się stało, gdyby wynosiła 100% w kierunku urojonym?

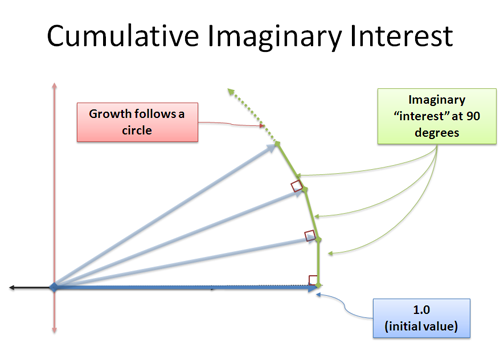
Teraz, nasze nowo powstałe odsetki dodają nam w kierunku 90 stopni. O dziwo, nie zmienia to naszej długości — jest to podchwytliwa koncepcja, ponieważ wydaje się, że tworzy trójkąt, w którym przeciwprostokątna musi być większa. Mamy do czynienia z ograniczeniem, a dodatkowa odległość mieści się w określonym przez nas marginesie błędu. Jest to coś, czym chcę się zająć innego dnia, ale uwierz mi na słowo: ciągły prostopadły wzrost będzie cię obracał. To jest serce sinusa i cosinusa, gdzie twoja zmiana jest prostopadła do twojej aktualnej pozycji, a ty poruszasz się po okręgu.

Stosujemy i jednostek wzrostu w nieskończenie małych przyrostach, z których każdy popycha nas pod kątem 90 stopni. Nie ma „coraz szybszego” obrotu – zamiast tego pełzamy po obwodzie na odległość |i| = 1 (wielkość i).

I hej — odległość pełzania po okręgu to kąt w radianach! Znaleźliśmy inny sposób na opisanie ruchu kołowego!

Aby uzyskać ruch kołowy: Zmieniaj w sposób ciągły, obracając się pod kątem 90 stopni (vel urojona szybkość wzrostu).

Więc wzór Eulera mówi „wykładniczy, urojony wzrost wytycza okrąg”. A ta ścieżka jest taka sama jak poruszanie się po okręgu za pomocą sinusa i cosinusa w płaszczyźnie urojonej.

W tym przypadku słowo „wykładniczy” jest mylące, ponieważ poruszamy się po okręgu ze stałą prędkością. W większości dyskusji przyjmuje się, że wzrost wykładniczy ma efekt kumulacyjny, składany.

Kilka przykładów

Nie bardzo mi wierzysz, prawda? Oto kilka przykładów i jak myśleć o nich intuicyjnie.

Przykład: $e^i$

Gdzie jest x? Intuicyjnie, bez wyciągania kalkulatora, wiemy, że oznacza to „podróż o 1 radian wzdłuż okręgu jednostkowego”. W mojej głowie widzę, jak „e” próbuje rosnąć o 1 na 100% w tym samym kierunku, ale i przesuwa piłkę i zmusza „1” do wzrostu wzdłuż krawędzi okręgu:

Nie jest to najładniejsza liczba, ale jest. Pamiętaj, aby ustawić swój kalkulator w trybie radianów, gdy będziesz to wpisywać.

Przykład: $3^i$

To jest podchwytliwe — nie jest w naszym standardowym formacie. Ale pamiętaj,

Chcemy mieć początkowy wzrost 3x na koniec okresu, czyli natychmiastowe tempo ln(3). Ale, i przychodzi i zmienia to tempo ln(3) na „i * ln(3)”:

Myśleliśmy, że będziemy się przekształcać w regularnym tempie ln(3), trochę szybciej niż 100% ciągłego wzrostu, ponieważ e wynosi około 2,718. Ale o nie, i obrócił nas wokół: teraz przekształcamy się w tempie urojonym, co oznacza, że po prostu obracamy się wokół. Gdyby i było zwykłą liczbą, taką jak 4, sprawiłoby to, że roślibyśmy 4x szybciej. Teraz rośniemy z prędkością ln(3), ale w bok.

Powinniśmy spodziewać się liczby złożonej na okręgu jednostkowym — nie ma nic w tempie wzrostu, co mogłoby zwiększyć nasze rozmiary. Rozwiązywanie równania:

Więc, zamiast skończyć na „1” jednostce wokół koła (jak $e^i$), skończymy na ln(3) jednostkach wokół.

Przykład: $i^i$

Kilka miesięcy temu, to doprowadziłoby mnie do łez. Ale nie dzisiaj! Rozbijmy transformacje:

Zaczynamy od 1 i chcemy ją zmienić. Jak w rozwiązaniu $3^i$, jaka jest chwilowa stopa wzrostu reprezentowana przez i jako bazę?

Hrm. Normalnie zrobilibyśmy ln(x), aby uzyskać tempo wzrostu potrzebne do osiągnięcia x na końcu 1 jednostki czasu. Ale dla wyimaginowanego tempa? Musimy się nad tym zastanowić.

Aby zacząć od 1 i rosnąć do i, musimy zacząć się obracać na początku. Jak szybko? Cóż, musimy uzyskać 90 stopni (pi/2 radianów) w 1 jednostce czasu. Zatem nasze tempo to $i \frac{pi}{2}$. Pamiętaj, że nasze tempo musi być urojone, ponieważ obracamy się, a nie rośniemy! Zwykłe stare $frac{pi}{2}$ wynosi około 1.57 i skutkuje regularnym wzrostem.

To powinno mieć sens: aby zamienić 1.0 na i na końcu 1 jednostki, powinniśmy obrócić $frac{pi}{2}$ radianów (90 stopni) w tym czasie. Tak więc, aby uzyskać „i” możemy użyć $e^{i \frac{pi}{2}}$.

Phew. To opisuje i jako podstawę. A co z wykładnikiem?

Cóż, drugie i mówi nam o zmianie naszego tempa – tak, tego tempa, które tak długo rozgryzaliśmy! Więc zamiast obracać się z prędkością $i \frac{pi}{2}$, co oznacza podstawa i, przekształcamy tempo na:

I’s cancel and make the growth rate real again! Obróciliśmy naszą stopę i popchnęliśmy się do liczb ujemnych. A ujemna stopa wzrostu oznacza, że się kurczymy – powinniśmy oczekiwać, że $i^i$ sprawi, że rzeczy będą mniejsze. I tak się dzieje:

Tada! (Wyszukaj „i^i” w Google, aby użyć jego kalkulatora)

Odetchnij: Możesz intuicyjnie dowiedzieć się, jak powinny zachowywać się urojone podstawy i urojone wykładniki. Whoa.

And as a bonus, you figured out ln(i) — to make $e^x$ become i, make e rotate $\frac{\pi}{2}$ radians.

Example: (i^i)^i

Podwójny wykładnik urojony? Jeśli się upierasz. Po pierwsze, wiemy jakie będzie nasze tempo wzrostu wewnątrz nawiasu:

Otrzymujemy ujemne (malejące) tempo wzrostu wynoszące -pi/2. A teraz ponownie modyfikujemy to tempo o i:

I teraz mamy ujemny obrót! Obracamy się po okręgu z prędkością $-alfrac{pi}{2}$ na jednostkę czasu. Jak długo to potrwa? Cóż, na samym szczycie tego łańcucha wykładników znajduje się dorozumiana jednostka czasu „1”; domyślnie jest to 1 jednostka czasu (tak jak $e = e^1$). 1 jednostka czasu daje nam obrót o $-alfrac{pi}{2}$ radianów (-90 stopni) lub -i!

A gdybyśmy podnieśli ten szalony wynik do kwadratu:

To „tylko” dwukrotny obrót: 2 jest liczbą regularną, więc podwaja nasz obrót do pełnego -180 stopni w jednostce czasu. Można też spojrzeć na to jako na zastosowanie obrotu o 90 stopni dwa razy z rzędu.

Na pierwszy rzut oka, są to naprawdę dziwne wykładniki. Ale z naszych analogii możemy wziąć je w kroku.

Kompleksowy wzrost

Możemy mieć rzeczywisty i urojony wzrost w tym samym czasie: część rzeczywista skaluje nas w górę, a część urojona obraca nas wokół:

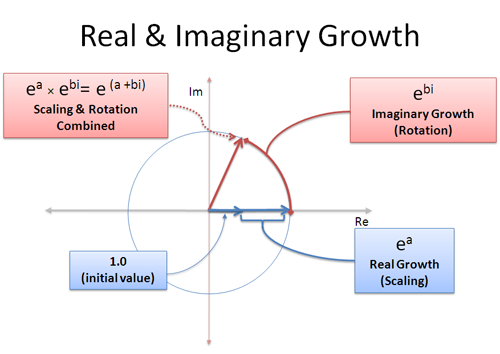
Złożona stopa wzrostu jak (a + bi) jest mieszanką rzeczywistego i urojonego wzrostu. Część rzeczywista a, oznacza „rosnąć na 100% przez a sekund”, a część urojona b oznacza „obracać się przez b sekund”. Pamiętaj, że obroty nie mają korzyści z potęgowania, ponieważ ciągle „pchasz” w innym kierunku – obroty sumują się liniowo.

Mając to na uwadze, możemy reprezentować dowolny punkt na okręgu o dowolnym rozmiarze używając (a+bi)! Promień to $e^a$, a kąt jest określony przez $e^{bi}$. To tak, jakby umieścić liczbę w expand-o-tronie na dwa cykle: raz, aby powiększyć ją do odpowiednich rozmiarów (a sekund), drugi raz, aby obrócić ją do odpowiedniego kąta (b sekund). Lub, można obrócić go najpierw, a następnie rosnąć!

Powiedzmy, że chcemy znać kwotę wzrostu, aby dostać się do 6 + 8i. To jest naprawdę prośba o logarytm naturalny liczby urojonej: jak zwiększyć e, aby uzyskać (6 + 8i)?

• Radius: Jak dużego okręgu potrzebujemy? Cóż, wielkość jest równa $sqrt{6^2 + 8^2} = \sqrt{100} = 10$. Co oznacza, że musimy rosnąć przez ln(10) = 2,3 sekundy, aby osiągnąć tę ilość.
• Liczba do obrócenia: Jaki jest kąt tego punktu? Możemy użyć arctan, aby to obliczyć: atan(8/6) = 53 stopnie = .93 radian.
• Połącz wynik: ln(6+8i) = 2.3 + .93i

To znaczy, że możemy osiągnąć losowy punkt (6 + 8i), jeśli użyjemy $e^{2.3 + .93i}$.

Dlaczego to jest użyteczne?

Wzór Eulera daje nam inny sposób na opisanie ruchu po okręgu. Ale mogliśmy to już zrobić za pomocą sinusa i cosinusa — co jest takiego specjalnego?

Wszystko sprowadza się do perspektywy. Sinus i cosinus opisują ruch w kategoriach siatki, wykreślając współrzędne poziome i pionowe.

Formuła Eulera używa współrzędnych biegunowych — jaki jest twój kąt i odległość? Ponownie, są to dwa sposoby opisania ruchu:

• System siatkowy: Idź 3 jednostki na wschód i 4 jednostki na północ
• Współrzędne biegunowe: Przejdź 5 jednostek pod kątem 53,13 stopni

W zależności od problemu bardziej przydatne są współrzędne biegunowe lub prostokątne. Wzór Eulera pozwala nam na konwersję między tymi dwoma, aby użyć najlepszego narzędzia do pracy. Ponadto, ponieważ $e^{ix}$ można przekształcić na sinus i cosinus, możemy przepisać wzory w trygonie jako wariacje na temat e, co jest bardzo przydatne (nie trzeba zapamiętywać sin(a+b), można to wyprowadzić — więcej o tym kiedy indziej). I to jest piękne, że każda liczba, rzeczywista czy złożona, jest wariacją na temat e.

Ale użyteczność, schmutility: najważniejszym wynikiem jest świadomość, że zaskakujące równania mogą stać się intuicyjne dzięki odpowiednim analogiom. Nie pozwól, aby piękne równania, takie jak formuła Eulera, pozostały magicznym zaklęciem — bazuj na analogiach, które znasz, aby dostrzec spostrzeżenia wewnątrz równania.

Szczęśliwa matematyka.

Dodatek

Screencast był zabawny, a informacje zwrotne są zdecydowanie mile widziane. Myślę, że to pomaga pomysłom pop, a chodzenie przez artykuł pomogło mi znaleźć luki w mojej intuicji.

• Brian Slesinsky ma zgrabną prezentację na temat formuły Eulera
• Visual Complex Analysis ma świetną dyskusję na temat formuły Eulera — zobacz str. 10 w Google Book Preview
• Zrobiłem wykład na Math and Analogies, który wyjaśnia Tożsamość Eulera bardziej wizualnie:

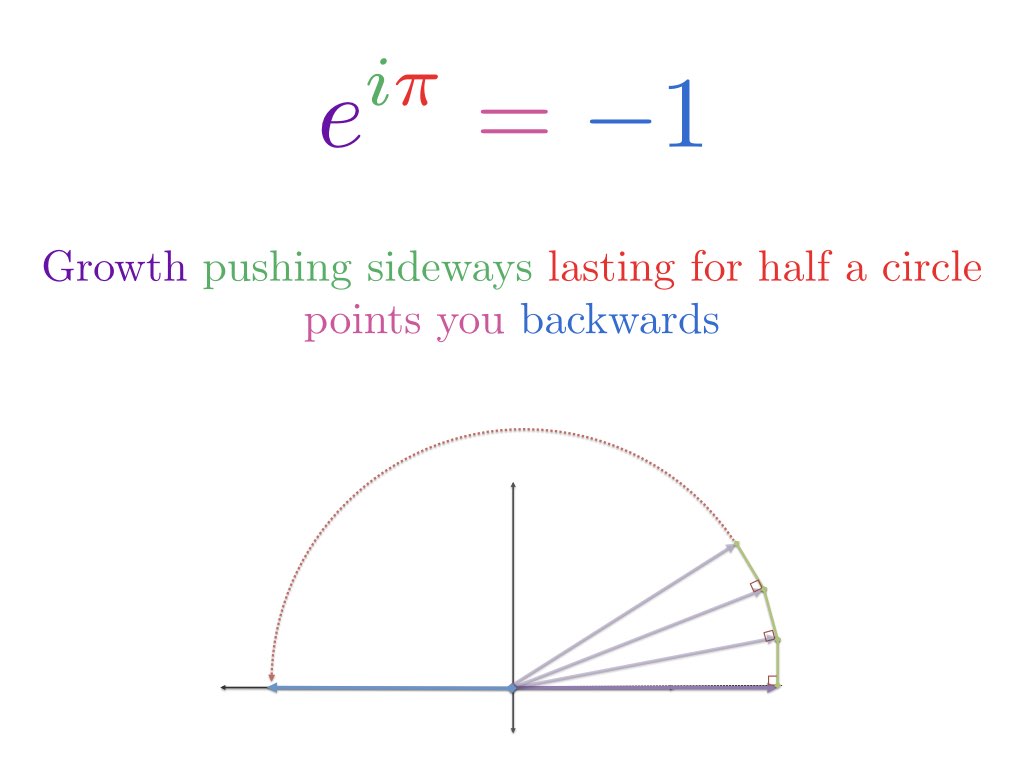
Other Posts In This Series

1. A Visual, Intuitive Guide to Imaginary Numbers
2. Intuitive Arithmetic With Complex Numbers
3. Understanding Why Complex Multiplication Works
4. Intuitive Guide to Angles, Stopnie i radiany
5. Intuicyjne rozumienie wzoru Eulera
6. Intuicyjny przewodnik po transformacie Fouriera
7. Intuicyjny przewodnik po konwolucji
8. Intuicyjny przewodnik po konwolucji
9. Intuicyjne rozumienie fal sinusoidalnych
10. Intuicyjny przewodnik po algebrze liniowej
11. Intuicja programisty w mnożeniu macierzy
12. Mnożenie binarne vs. Wykładniki urojonego mnożenia

Mnożenie a wykładniki urojonego mnożenia