W wskazówce miesiąca (TOTM) z listopada 2011 r. przedstawiliśmy obliczenia sprężarki w studium przypadku. Porównaliśmy wyniki uzyskane metodą rygorystyczną z wartościami uzyskanymi metodami skrótowymi. Metoda rygorystyczna opierała się na równaniu stanu Soave-Redlich-Kwong (SRK) do obliczania wymaganych entalpii i entropii. Entalpie i entropie są wykorzystywane do określenia zapotrzebowania na moc i temperatury tłoczenia. Wyniki wskazały, że dokładność metody skrótu jest wrażliwa na wartość współczynnika pojemności cieplnej w stanie gazu idealnego, k.
Z samego tylko obliczeniowego punktu widzenia, obliczanie mocy jest szczególnie wrażliwe na specyfikację masowego natężenia przepływu, temperatury i ciśnienia ssania oraz temperatury i ciśnienia tłoczenia. Sprężarka będzie pracować przy zmiennych wartościach zmiennych wpływających na jej wydajność. Dlatego najtrudniejszą częścią obliczeń sprężarki jest określenie rozsądnego zakresu dla każdej zmiennej, a nie same obliczenia. Referent podkreśla, że stosowanie jednej wartości dla każdej zmiennej nie jest właściwym sposobem oceny systemu sprężania.
Normalnie, obliczenia termodynamiczne są wykonywane dla procesu idealnego (odwracalnego). Wyniki procesu odwracalnego są następnie dostosowywane do świata rzeczywistego poprzez zastosowanie sprawności termodynamicznej. W procesie sprężania istnieją trzy idealne procesy, które można zobrazować: 1) proces izotermiczny (PV1=C1), 2) proces izentropowy (PVk=C2) i 3) proces politropowy (PVn=C3). Każdy z tych procesów może być odpowiednio użyty jako podstawa do oszacowania zapotrzebowania na moc sprężania za pomocą obliczeń ręcznych lub komputerowych. Proces izotermiczny jest jednak rzadko używany jako podstawa, ponieważ normalny przemysłowy proces sprężania nie jest nawet w przybliżeniu prowadzony w stałej temperaturze.
Zauważ, że Dresser Rand wykonuje sporo pracy z „prawie stałotemperaturowym” procesem sprężania, szczególnie dla sprężania CO2 z kominów wentylacyjnych. W tym TOTM pokażemy, jak określić wydajność sprężarki na podstawie zmierzonego natężenia przepływu, składu, temperatur i ciśnień na ssaniu i tłoczeniu. Rozważone zostaną rygorystyczne obliczenia oparte na równaniu stanu oraz metoda skrócona, a wyniki zostaną porównane.
Wydajność sprężarki
Wydajność sprężarki różni się w zależności od jej typu, rozmiaru i wydajności. Można je określić (później) jedynie poprzez test sprężarki, chociaż producenci sprężarek mogą zazwyczaj przedstawić dobre dane szacunkowe. Dla celów planowania, odniesienia sugerują następujące wartości dla ogólnych współczynników efektywności:
Tabela 1. Całkowita wydajność sprężarki
|
Typ sprężarki |
Sprawność, η |
|
|
Odśrodkowa |
0.70 – 0,85 |
|
|
Wysokoobrotowe |
0,72 – 0,85 |
|
|
Niskoobrotowe |
0,75 – 0,90 |
0.75 – 0,90 |
|
Śruba obrotowa |
0,65 – 0,75 |
Odniesienie wskazuje, że te ogólne współczynniki efektywności obejmują tarcie gazu w sprężarce, straty mechaniczne (łożyska, uszczelnienia, przekładnia itp.) oraz straty w przekładni. Efektywność mechaniczna różni się w zależności od wielkości i typu sprężarki, ale 95% jest przydatną wartością do planowania. Przy obliczaniu wysokości podnoszenia sprężarki i temperatury tłoczenia stosuje się współczynnik wydajności izentropowej lub politropowej (współczynnik izentropowy jest czasami nazywany współczynnikiem adiabatycznym). Dodanie 3-4 % współczynnika efektywności (straty mechaniczne) do ogólnych współczynników efektywności podanych w tabeli 1 daje na ogół dobre oszacowanie współczynnika termodynamicznego.
Aby ocenić wydajność istniejącej sprężarki, należy obliczyć jej efektywność (η) i zapotrzebowanie na moc.
Właściwości znane i mierzone to:
a. Objętościowe natężenie przepływu gazu w warunkach standardowych (qS) lub masowe natężenie przepływu gazu ()
b. Skład gazu (zi)
c. Ciśnienie ssania (P1) i temperatura (T1)
d. Ciśnienie wylotowe (P2) i temperatura (T2)
Oszacowanie wydajności – rygorystyczna metoda
Sercem każdego komercyjnego oprogramowania do symulacji przepływu procesu jest równanie stanu. Ze względu na ich prostotę i względną dokładność, stosuje się sześcienne EOS, takie jak Soave Redlich-Kwong (SRK) lub Peng-Robinson. Równania te są używane do obliczania równowagi para-ciecz (VLE), entalpii (h) i entropii (s). Przy odpowiednich współczynnikach interakcji binarnej, wyniki symulacji procesu dla tych dwóch równań są praktycznie takie same. Dlatego w niniejszej pracy zastosowano tylko SRK.
Wydajność izentropowa jest zdefiniowana przez
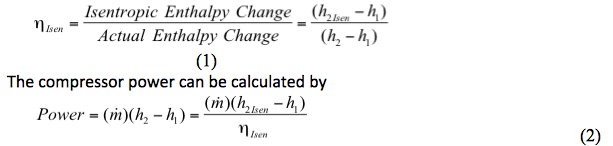
Gdzie:
ηIsen = Sprawność izentropowa
h1 = Entalpia ssania obliczona przy P1, T1, i składzie (zi)
h2 = Entalpia tłoczenia obliczona przy P2, T2, i skład (zi)
h2Isen = Izentropowa entalpia tłoczenia w P2 (lub T2), S2Isen =S1, i skład (zi)
![]() = Masowe natężenie przepływu
= Masowe natężenie przepływu
Obliczanie sprawności lub mocy sprężarki obejmuje dwa kroki
1. Wyznaczenie idealnej lub izentropowej (odwracalnej i adiabatycznej) zmiany entalpii (h2Isen-h1) procesu sprężania.
2. Wyznaczenie rzeczywistej zmiany entalpii (h2-h1).
Obliczenia krok po kroku na podstawie EOS:
a. Założyć stan ustalony, tj.
b. Przyjąć, że skład nadawy pozostaje niezmieniony
c. Obliczyć entalpię ssania h1=f(P1, T1, i zi) oraz entropię s1=f(P1, T1, i zi) metodą EOS
d. Założyć proces izentropowy i wyznaczyć s2Isen = f (P2, T2Isen, zi) = s1 = f (P1, T1, zi).
e. Obliczyć entalpię idealną (h2Isen) w stanie rozładowania dla znanych zi, T2 (lub P2) i s2Isen.
f. Obliczyć entalpię rzeczywistą (h2) w stanie rozładowania dla znanych zi, T2 i P2.
g. Obliczyć sprawność izentropową wg równania 1: µIsen = (h2Isen – h1)/(h2 – h1)
h. Oblicz moc według Równania 2: ![]()
Estimating Efficiency – Shortcut Method
Wykładnik drogi izentropowej (k) lub współczynnik pojemności cieplnej gazu idealnego (k=CP/CV) można obliczyć za pomocą zależności przedstawionej w TOTM z maja 2013 r:
![]()
Gdzie:
T = Temperatura, K (°R)
![]() = Gęstość względna gazu; stosunek masy cząsteczkowej gazu do masy cząsteczkowej powietrza
= Gęstość względna gazu; stosunek masy cząsteczkowej gazu do masy cząsteczkowej powietrza
A = 0.000272 (0.000151)
Faktyczną temperaturę tłoczenia w oparciu o ścieżkę izentropową można oszacować przez

rozwiązanie dla sprawności izentropowej,
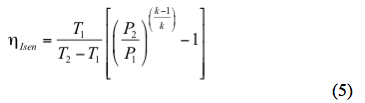
Podobnie, rzeczywistą temperaturę tłoczenia na podstawie ścieżki politropowej można oszacować przez

Rozwiązanie powyższego równania dla współczynnika ścieżki politropowej (n):

Podobnie, rzeczywista temperatura tłoczenia na podstawie ścieżki politropowej może być oszacowana (ηPoly) przez:

Głowica izentropowa jest obliczana przez
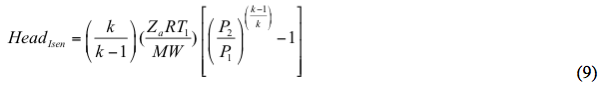
Podobnie, głowica politropowa jest obliczana przez
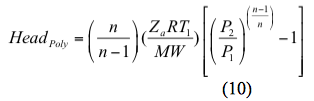
Dla procesu izentropowego (odwracalnego i adiabatycznego) moc jest obliczana przez
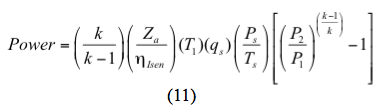
Albo dla procesu politropowego moc jest obliczana przez
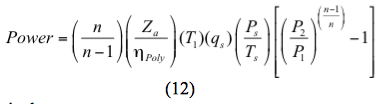
Alternatywnie:
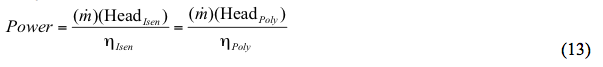
Gdzie:
Head = Głowica sprężarki, m (ft)
Power = Moc sprężarki, kW (HP)
R = Uniwersalna stała gazowa, 848 kg-m/(kmol-K) lub (1545 ft-lbf/(lbmol-°R))
PS = Ciśnienie stanu normalnego, kPa (psia)
P1 = Ciśnienie ssania, kPa (psia)
P2 = Ciśnienie tłoczenia, kPa (psia)
TS = Temperatura stanu normalnego, K (°R)
T1 = Temperatura ssania, K (°R)
T2 = Temperatura tłoczenia, K (°R)
qS = Objętościowe natężenie przepływu gazu w warunkach standardowych, Sm3/d (scf/dzień)
Za = Średni współczynnik ściśliwości gazu = (Z1+Z2)/2
Z1 = Współczynnik ściśliwości gazu w stanie ssania
Z2 = Współczynnik ściśliwości gazu w stanie tłoczenia
MW = Masa cząsteczkowa gazu
Obliczenie mocy należy wykonać dla każdego stopnia sprężania, a następnie zsumować dla wszystkich stopni podłączonych do jednego sterownika.
Obliczenia krok po kroku dla metody skróconej
a. Obliczyć wykładnik izentropowy (k) według równania 3, używając średniej temperatury zdefiniowanej przez T = (T1+3T2)/4. Taka postać średniej temperatury została zdefiniowana w celu uzyskania lepszej zgodności pomiędzy wynikami uzyskanymi metodą rygorystyczną i skróconą.
b. Obliczyć sprawność izentropową (ηIsen) według równania 5.
c. Obliczyć współczynnik politropowy (n) wg równania 7.
d. Obliczyć sprawność politropową (ηPoly) wg równania 8.
e. Obliczyć głowice izentropową i politropową, odpowiednio według równań 9 i 10.
f. Obliczyć wymaganą moc na stopień za pomocą równania 11 lub 12.
Studium przypadku
Mieszanina gazu ziemnego jest sprężana za pomocą trzystopniowej sprężarki odśrodkowej. Schemat przepływu procesu pokazano na rysunku 1. Pomiary ciśnienia i temperatury dla każdego etapu przedstawiono w tabeli 1. Zmierzony skład zasilania, natężenie przepływu oraz obliczoną masę cząsteczkową i gęstość względną przedstawiono w tabeli 2.
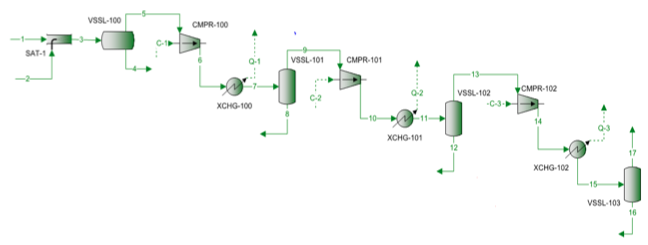
Rysunek 1. Schemat przepływu procesu dla 3-stopniowego sprężania
Tabela 1. Zmierzona temperatura i ciśnienie dla trzech etapów sprężania
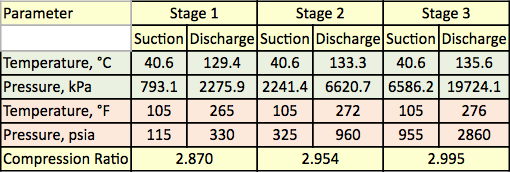
Tabela 2. Analiza gazu i natężenie przepływu dla trzech stopni sprężania
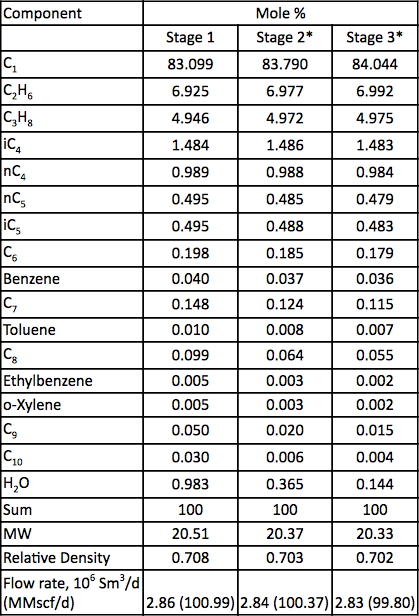
* Obliczone
Wyniki i dyskusje
Schemat przepływu procesu przedstawiony na rysunku 1 został zasymulowany przez oprogramowanie ProMax w celu wykonania rygorystycznych obliczeń z wykorzystaniem SRK EOS. Program obliczył sprawności politropowe i izentropowe, głowice i moc sprężania. Program obliczył również wykładnik ścieżki izentropowej (k) oraz wykładnik ścieżki politropowej (n). Obliczone wyniki przedstawiono w tabeli 2 dla wszystkich trzech etapów w pozycjach SRK. Obliczenia wykonane przez ProMax są bardzo podobne do obliczeń krok po kroku od a do h opisanych w części rygorystycznej. Tabela 2 przedstawia również wyniki obliczeń skrótowych dla odpowiednich wartości w rubryce skrót. Obliczenia metodą skróconą są oparte na metodzie krok po kroku od a do f opisanej w części poświęconej metodzie skróconej. W tabeli 2 przedstawiono również procentowe wartości błędu między metodą ścisłą a metodami skróconymi dla każdego etapu. Tabela 2 wskazuje, że doskonałe uzgodnienia uzyskuje się dla etapów 1 i 2. Jednak większe odchylenia obserwuje się dla wykładników izetropowego i politropowego etapu 3 ze względu na pracę pod wysokim ciśnieniem, która zbytnio odbiegała od warunków idealnego stanu gazu.
Tabela 3. Podsumowanie wyników obliczeń rygorystycznych i skrótowych
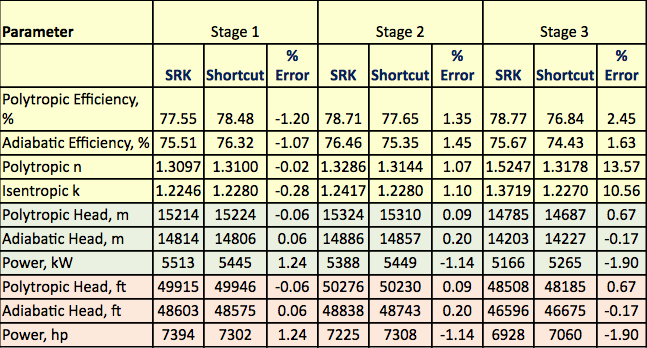
Wnioski
Tabela 2 wskazuje, że istnieją dobre uzgodnienia pomiędzy wynikami skrótowymi i rygorystycznymi. Różnice pomiędzy wynikami metody ścisłej i skróconej dla obliczeń obiektów i celów planistycznych są pomijalne. Dla etapu 3, z powodu pracy pod wysokim ciśnieniem i zbyt dużego odchylenia od stanu gazu idealnego, obserwuje się większy błąd dla wykładnika izentropowego (k).
Obliczony wykładnik izentropowy (k) w programie ProMax nie jest stosunkiem pojemności cieplnej (CP/CV) w stanie gazu idealnego. Jest to wartość wykładnika izentropowego, która jest wymagana do uzyskania ścieżki izentropowej od wlotu do wylotu. Jego wartość jest obliczana jako całka tej ścieżki. Tak więc jest to w pewnym sensie „średnia” wartość reprezentująca prawdziwą ścieżkę izentropową. Dla gazów idealnych, wartość ta byłaby równa stosunkowi (CP/CV).
Ten błąd w „k” ilustruje również znaczenie określenia, która korelacja ma być użyta podczas zamawiania testu wydajności (tj. odnieść się do ASME PTC-10 w celu uzyskania dodatkowych szczegółów), tak aby klient i sprzedawca byli na tej samej umowie w odniesieniu do masy cząsteczkowej (MW) i k dla badanego płynu. W celu uzyskania dalszych szczegółów należy odnieść się do referencji oraz TOTM z sierpnia i września 2010 r.
Warto również zauważyć, że podczas wyznaczania trendu „n” i wydajności politropowej w celu oceny stanu maszyny, względna dokładność przyrządów/sprzętu pomiarowego (przetworniki temperatury i ciśnienia) oraz odwzorowanie wydajności sprężarki na oryginalną krzywą wydajności (rzeczywiste objętościowe natężenie przepływu gazu w funkcji prędkości obrotowej) wprowadza wiele potencjalnych błędnych źródeł do tej codziennej oceny.
Zauważ, że dokładność metod skróconych zależy od wartości k i n. Definicja średniej temperatury w metodzie skróconej została dostosowana w celu uzyskania lepszego dopasowania wykładnika ścieżki izentropowej (k) obliczonego metodą rygorystyczną.
Aby dowiedzieć się więcej o podobnych przypadkach i jak zminimalizować problemy operacyjne, sugerujemy wzięcie udziału w naszych kursach G4 (Gas Conditioning and Processing), PF4 (Oil Production and Processing Facilities), ME46 (Compressor Systems-Mechanical Design and Specifications) i ME44 (Fundamentals of Pump and Compressors Systems).
PetroSkills oferuje ekspertyzy konsultingowe na ten i wiele innych tematów. Aby uzyskać więcej informacji na temat tych usług, odwiedź naszą stronę internetową pod adresem http://petroskills.com/consulting lub napisz do nas na adres [email protected].
Dr Mahmood Moshfeghian
Referencje:
3. Soave, G., Chem. Eng. Sci., Vol. 27, pp. 1197-1203, 1972.
4. Peng, D. Y., and Robinson, D. B., Ind. Eng. Chem. Fundam., Vol. 15, s. 59, 1976.
5. ProMax 3.2, Bryan Research and Engineering, Inc, Bryan, Texas, 2014.
6. ASME PTC-10, „Performance test Code on Compressors and Exhausters”, 1997.
7. Honeywell, J. „Ważne aspekty testowania sprężarek odśrodkowych – część 1”, Wskazówka miesiąca, sierpień 2010
8. Honeywell, J. „Ważne aspekty testowania sprężarek odśrodkowych – część 2”, Wskazówka miesiąca, wrzesień 2010
.