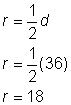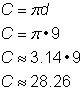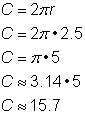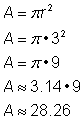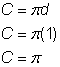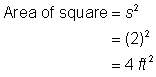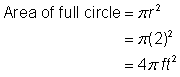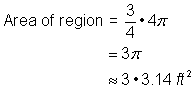Kręgi
Cel(e) nauczania
– Zidentyfikować właściwości okręgów.
– Znaleźć obwód okręgu.
– Znaleźć pole okręgu.
– Znaleźć pole i obwód złożonych figur geometrycznych.
Wprowadzenie
Kręgi są powszechnym kształtem. Widzisz je wszędzie – koła w samochodzie, Frisbees przechodzące przez powietrze, płyty kompaktowe dostarczające dane. To wszystko są okręgi.
Okrąg jest dwuwymiarową figurą tak jak wielokąty i czworokąty. Jednakże, okręgi są mierzone inaczej niż te inne kształty – trzeba nawet użyć kilku różnych terminów, aby je opisać. Spójrzmy na ten interesujący kształt.
Właściwości okręgów
Okrąg reprezentuje zbiór punktów, z których wszystkie są w tej samej odległości od stałego, środkowego punktu. Ten stały punkt nazywany jest środkiem. Odległość od środka okręgu do dowolnego punktu na okręgu nazywamy promieniem.
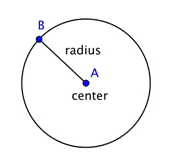
Gdy dwa promienie (liczba mnoga od radius) są połączone razem, aby utworzyć odcinek linii w poprzek okręgu, mamy średnicę. Średnica okręgu przechodzi przez środek okręgu i ma swoje punkty końcowe na samym okręgu.
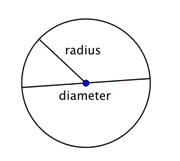
Średnica dowolnego okręgu jest dwa razy dłuższa od długości jego promienia. Można ją przedstawić za pomocą wyrażenia 2r, czyli „dwa razy promień”. Jeśli więc znasz promień okręgu, możesz pomnożyć go przez 2, aby znaleźć średnicę; oznacza to również, że jeśli znasz średnicę okręgu, możesz podzielić ją przez 2, aby znaleźć promień.
|
Przykład |
||
|
Problem |
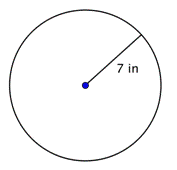
Znajdź średnicę okręgu.
|
|
|
d = 2r d = 2(7) d = 14 |
Średnica jest dwa razy większa od promienia, czyli 2r. Promień tego okręgu wynosi 7 cali, więc średnica wynosi 2(7) = 14 cali. |
|
|
Odpowiedź |
Średnica wynosi 14 cali. |
|
|
Przykład |
||
|
Problem |
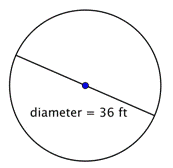
Znajdź promień okręgu.
|
|
|
|
Promień jest połową średnicy, czyli |
|
|
Odpowiedź |
Promień wynosi 18 stóp. |
|
Obwód
Dystans wokół okręgu nazywamy obwodem. (Przypomnijmy, że odległość wokół wielokąta to obwód.)
Jedną z interesujących własności okręgów jest to, że stosunek obwodu okręgu do jego średnicy jest taki sam dla wszystkich okręgów. Bez względu na rozmiar okręgu, stosunek obwodu i średnicy będzie taki sam.
Poniżej podano kilka rzeczywistych pomiarów różnych przedmiotów. Pomiary są dokładne do najbliższego milimetra lub ćwierć cala (w zależności od używanej jednostki miary). Spójrz na stosunek obwodu do średnicy dla każdego z nich – mimo, że przedmioty są różne, stosunek dla każdego z nich jest w przybliżeniu taki sam.
|
Przedmiot |
Obwód (C) (zaokrąglony do najbliższej setnej części) |
.
Średnica (d) |
Ratio |
|
Miseczka |
253 mm . |
79 mm |
|
|
Kwarta |
84 mm |
27 mm |
|
|
Miska |
37.25 in |
11.75 in |
|
Obwód i średnica są pomiarami przybliżonymi, ponieważ nie ma możliwości dokładnego zmierzenia tych wymiarów. Gdyby jednak udało się je zmierzyć dokładniej, okazałoby się, że stosunek ![]() dla każdego z podanych przedmiotów zmierzałby do 3,14. Matematyczna nazwa stosunku
dla każdego z podanych przedmiotów zmierzałby do 3,14. Matematyczna nazwa stosunku ![]() to pi i jest reprezentowana przez grecką literę
to pi i jest reprezentowana przez grecką literę ![]() .
.
![]() jest niekończącą się, niepowtarzającą się liczbą dziesiętną, więc nie da się jej zapisać w całości. Pierwsze 10 cyfr
jest niekończącą się, niepowtarzającą się liczbą dziesiętną, więc nie da się jej zapisać w całości. Pierwsze 10 cyfr ![]() to 3,141592653; często zaokrągla się ją do 3,14 lub szacuje jako ułamek
to 3,141592653; często zaokrągla się ją do 3,14 lub szacuje jako ułamek ![]() . Zauważ, że zarówno 3,14 jak i
. Zauważ, że zarówno 3,14 jak i ![]() są przybliżeniami liczby
są przybliżeniami liczby ![]() i są używane w obliczeniach, w których nie jest ważna dokładność.
i są używane w obliczeniach, w których nie jest ważna dokładność.
Ponieważ wiesz, że stosunek obwodu do średnicy (lub ![]() ) jest stały dla wszystkich okręgów, możesz użyć tej liczby do znalezienia obwodu okręgu, jeśli znasz jego średnicę.
) jest stały dla wszystkich okręgów, możesz użyć tej liczby do znalezienia obwodu okręgu, jeśli znasz jego średnicę.
![]() =
= ![]() , więc C =
, więc C = ![]() d
d
Ale skoro d = 2r, to C = ![]() d =
d = ![]() (2r) = 2
(2r) = 2![]() r.
r.
Obwód okręgu
Aby znaleźć obwód (C) okręgu, skorzystaj z jednego z następujących wzorów:
Jeżeli znasz średnicę (d) okręgu: ![]()
Jeśli znasz promień (r) okręgu: ![]()
|
Przykład |
||
|
Problem |
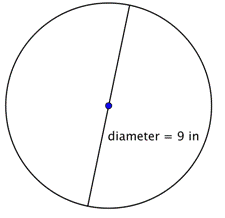
Znajdź obwód okręgu.
|
|
|
|
Aby obliczyć obwód, mając średnicę 9 cali, skorzystaj ze wzoru Ponieważ używasz przybliżenia dla |
|
|
Podpowiedź |
Obwód wynosi 9 |
|
|
Przykład |
||
|
Problem |
Znajdź obwód koła o promieniu 2.5 jardów. |
|
|
|
Aby obliczyć obwód okręgu o promieniu 2,5 jarda, skorzystaj ze wzoru |
|
|
Podpowiedź |
Obwód wynosi 5 |
|
Krąg ma promień 8 cali. Ile wynosi jego obwód, zaokrąglony do najbliższego cala?
A) 25 cali
B) 50 cali
C) 64 cale2
D) 201 cali
Powierzchnia
![]() jest ważną liczbą w geometrii. Używałeś jej już do obliczania obwodu koła. Używasz
jest ważną liczbą w geometrii. Używałeś jej już do obliczania obwodu koła. Używasz ![]() również wtedy, gdy obliczasz pole koła.
również wtedy, gdy obliczasz pole koła.
Powierzchnia okręgu
Aby znaleźć pole (A) okręgu, skorzystaj ze wzoru: ![]()
|
Przykład |
||
|
Problem |
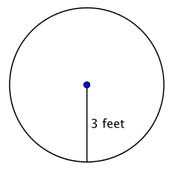
Znajdź pole koła.
|
|
|
|
Aby znaleźć pole tego okręgu, skorzystaj ze wzoru Pamiętaj, aby odpowiedź zapisać w jednostkach kwadratowych, ponieważ znajdujesz pole powierzchni. |
|
|
Odpowiedź |
Pole powierzchni wynosi 9 |
|
Guzik ma średnicę 20 milimetrów. Jakie jest pole powierzchni tego guzika? Skorzystaj z 3,14 jako przybliżenia ![]() .
.
A) 62,8 mm
B) 314 mm2
C) 400 mm2
D) 1256 mm2
Figury złożone
Teraz, gdy wiesz, jak obliczyć obwód i pole koła, możesz użyć tej wiedzy, aby znaleźć obwód i pole figur złożonych. Sztuką w rozwiązywaniu tego typu problemów jest zidentyfikowanie kształtów (i części kształtów) w ramach figury złożonej, obliczenie ich indywidualnych wymiarów, a następnie dodanie ich razem.
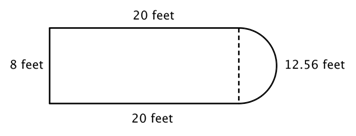
Na przykład, spójrz na poniższy obrazek. Czy możliwe jest znalezienie obwodu?
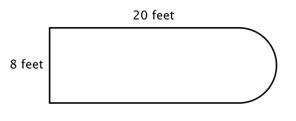
Pierwszym krokiem jest zidentyfikowanie prostszych figur w tej złożonej figurze. Możesz rozłożyć ją na prostokąt i półkole, jak pokazano poniżej.
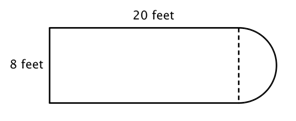
Wiesz jak znaleźć obwód prostokąta i wiesz jak znaleźć obwód koła. Tutaj, obwód trzech pełnych boków prostokąta wynosi 8 + 20 + 20 = 48 stóp. (Zauważ, że tylko trzy boki prostokąta dodadzą się do obwodu figury złożonej, ponieważ drugi bok nie jest na krawędzi; jest objęty półokręgiem!)
Aby znaleźć obwód półokręgu, użyj wzoru ![]() o średnicy 8 stóp, a następnie weź połowę wyniku. Obwód półkola wynosi
o średnicy 8 stóp, a następnie weź połowę wyniku. Obwód półkola wynosi ![]() , czyli około 12,56 stopy, więc całkowity obwód wynosi około 60,56 stopy.
, czyli około 12,56 stopy, więc całkowity obwód wynosi około 60,56 stopy.
|
Przykład |
||
|
Problem |
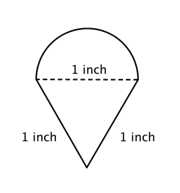
Znajdź obwód (z dokładnością do jednej setnej) figury złożonej, składającej się z półokręgu i trójkąta.
|
|
|
|
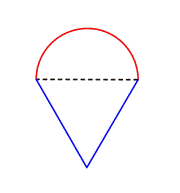
Zidentyfikuj mniejsze kształty wewnątrz figury złożonej. Ta figura zawiera półkole i trójkąt. |
|
|
Średnica (d) = 1
Obwód półkola = |
Znajdź obwód koła. Następnie podziel przez 2, aby znaleźć obwód półokręgu. |
|
|
|
|
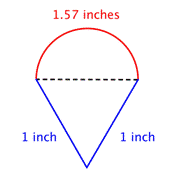
Znajdź całkowity obwód, dodając obwód półokręgu i długości dwóch nóg. Ponieważ nasz pomiar obwodu półkola jest przybliżony, obwód również będzie przybliżony. |
|
Odpowiedź |
W przybliżeniu 3.57 cali |
|
|
Przykład |
||
|
Problem |
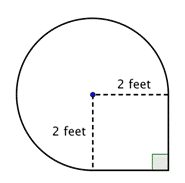
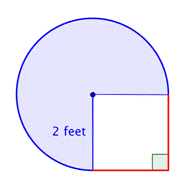
Znajdź pole figury złożonej, składającej się z trzech czwartych koła i kwadratu, z dokładnością do jednej setnej.
|
|
|
|
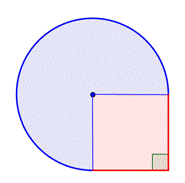
Zidentyfikuj mniejsze kształty w obrębie figury złożonej. Ta figura zawiera okrąg i kwadrat. Jeśli znajdziesz pole każdego z nich, możesz znaleźć pole całej figury. |
|
|
|
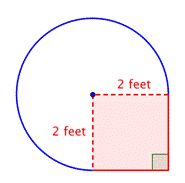
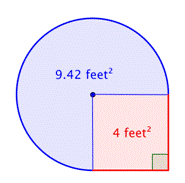
Znajdź pole kwadratu. |
|
|
|
|
Znajdź pole powierzchni okręgu. Promień wynosi 2 stopy. Zauważ, że obszar jest |
|
|
4 stopy2 + |
Dodaj oba regiony razem. Ponieważ Twój pomiar powierzchni okręgu jest przybliżony, powierzchnia figury również będzie przybliżona. |
|
Odpowiedź |
Powierzchnia wynosi w przybliżeniu 13.42 stóp2. |
|
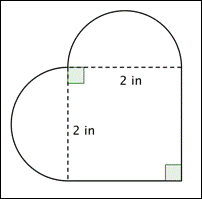
Jakie jest pole (z dokładnością do setnej części) figury przedstawionej poniżej? (Oba zaokrąglone regiony są półkolami.)
A) 16,56 cala2
B) 7,14 cala2
C) 4 in2
D) 3.14 in2
Podsumowanie
Kręgi są ważnym kształtem geometrycznym. Odległość wokół okręgu nazywana jest obwodem, a przestrzeń wewnątrz okręgu nazywana jest polem. Obliczenie obwodu i pola koła wymaga liczby zwanej pi (![]() ), która jest niekończącą się, niepowtarzającą się liczbą dziesiętną. Pi jest często przybliżane przez wartości 3,14 i
), która jest niekończącą się, niepowtarzającą się liczbą dziesiętną. Pi jest często przybliżane przez wartości 3,14 i ![]() . Możesz znaleźć obwód lub pole powierzchni złożonych kształtów – w tym kształtów, które zawierają sekcje kołowe – stosując wzory na obwód i pole w odpowiednich przypadkach.
. Możesz znaleźć obwód lub pole powierzchni złożonych kształtów – w tym kształtów, które zawierają sekcje kołowe – stosując wzory na obwód i pole w odpowiednich przypadkach.