
Galileo jest często uważany za ojca współczesnej nauki. Był on tym, który połączył zasady eksperymentu, teorii i matematyki w standardowe ramy. Prawdopodobnie bardziej niż ktokolwiek inny Galileusz był osobą odpowiedzialną za rozwój nowoczesnej nauki.
Mówi się, że Galileusz upuścił dwie stalowe kule o różnej masie, ale z tego samego materiału z krzywej wieży w Pizie i wylądowały one w tym samym czasie. Co jest niezwykłe w tym eksperymencie jest on wprowadził nową metodę robienia nauki, gdzie przeprowadzić eksperyment, aby przetestować hipotezę. Pokazał, że musimy zrobić więcej niż tylko myśleć, że coś jest prawdą, ale także musimy to udowodnić.

Galileusz znalazł interesujący paradoks, gdy był kierownikiem Katedry Matematyki na Uniwersytecie w Pizie.
Definicja: Paradoks, zwany też antynomią, to logicznie samozaprzeczalne stwierdzenie lub stwierdzenie sprzeczne z czyimś oczekiwaniem. (Wikipedia). (grecki: „para” = poza, „doxa” = wiara)
Paradoks Galileusza dotyczył określenia, czy dwa zbiory zawierające nieskończone obiekty są sobie równoważne. Na przykład, niech P będzie zbiorem liczb całkowitych dodatnich, gdzie P= {0,1,2,3,…} i E jest zbiorem liczb parzystych, gdzie E = {0,2,4,6,…}. Galileusz twierdził, że rozmiary tych dwóch zbiorów będą takie same, ponieważ możemy sparować każdą dodatnią liczbę całkowitą ze zbioru P z liczbami parzystymi ze zbioru E.

Jak więc rozmiary tych dwóch zbiorów będą takie same, gdy w E pojawi się „mniejsza” liczba? To zostało nazwane paradoksem Galileusza i rozpoczęło nową debatę na temat pojęcia nieskończoności.
Po Galileuszu, jego uczeń Evangelista Torricelli został kierownikiem Katedry Matematyki na Uniwersytecie w Pizie. Być może słyszeliście go z powodu jego prac na ciśnienie atmosferyczne i wynalazek barometru. Ponieważ Toricelli jest również zainteresowany w matematyce, pyta:
Czy to możliwe, aby mieć obiekt o skończonej objętości i nieskończonej powierzchni? W pierwszej kolejności, takie coś wydaje się mało prawdopodobne dla większości z nas. Jednak matematyka mówi nam, że taka rzecz może się zdarzyć. Torricelli odpowiedział na swoje pytanie sam i odkrył Toricelli’s Trumpet, którego powierzchnia jest nieskończona, ale którego objętość jest skończona. Jego odkrycie postrzegane jako „niesamowite” paradoks.
Przy okazji, istnieje istotna zasada w filozofii matematyki; Niezależnie od tego, z którą epoką filozofii lub matematyki masz do czynienia, jest ona związana z historią, kulturą i religią tego regionu. Dlatego trąbkę Toricellego nazywają również Rogiem Gabriela. Odniesienie jest tutaj do Biblii, ponieważ chrześcijanie wierzą, że anioł Gabriel będzie dmuchał w róg w Dniu Sądu Ostatecznego.
Więc jak tworzy się trąbka Toricellego? Wszyscy wiemy, jak wykreślić wykres y=x. Jeśli zamiast tego wykreślimy równanie y=1/x, gdzie x jest większe lub równe 1, wykres będzie wyglądał tak:
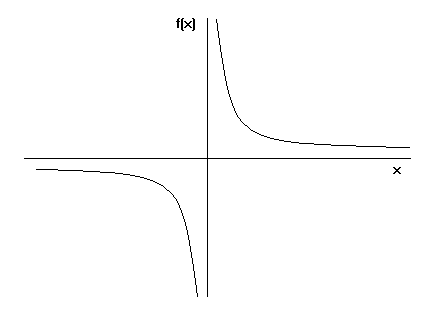
Gdy weźmiemy wykres y=1/x i obrócimy go wokół osi x, zobaczymy trąbkę Toricellego.

Na szczęście mamy w rękach wzory matematyczne, dzięki którym możemy obliczyć pole powierzchni i objętość trąbki Toricellego. Gdy zastosujemy poniższy wzór całkowania dla objętości trąbki, otrzymamy skończoną ilość.
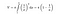
Jednakże, gdy zastosujemy wzór całkowania dla powierzchni trąbki, tym razem jej powierzchnia staje się nieskończona. Czyż ten wynik nie jest interesujący?
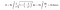
Ponieważ objętość trąbki Toricellego jest skończona, możemy ją wypełnić skończoną ilością farby. Dla przykładu załóżmy, że jej objętość wynosi 100 litrów. Idę do Home Depot i kupić 100 litrów farby i wypełnić go. Jednak to, co czyni to interesującym, to fakt, że pomalowałem nieskończoną powierzchnię tymi 100 litrami farby. Dziś większość ludzi nazywa ten paradoks „paradoksem malarza.”
Houston, mamy tu problem! Sytuacja, która jest niemożliwa w praktyce, staje się możliwa w matematyce. Jak więc trąbka Torricellego może być prawdziwa? Albo, jak możemy dokładnie dopasować wszystkie elementy zbiorów, podczas gdy jeden ze zbiorów jest podzbiorem innego w przykładzie Galileusza?
Powodem tych wszystkich konfliktów jest to, że pojęcie nieskończoności nie jest podobne do innych pojęć, które znamy, a to dezorientuje wielu ludzi. Galileusz mówi na swój paradoks,
„Tak, mój przyjacielu, istnieje nieskończoność. Daremne jest sprzeciwianie się temu. Zbiory, nad którymi pracuję, są przykładami zbiorów zamkniętych, które dotyczą nieskończoności. Zaczynają się w punkcie i ciągną się do nieskończoności, a jednak nadal są zbiorami. Jednak moje uwagi i pojęcia dotyczące nieskończoności muszą być inne niż te, których użyłbym dla wielkości skończonych. Jeśli masz do czynienia z wielkościami skończonymi, możesz powiedzieć, że 3 kilogramy są mniejsze niż 5 kilogramów, lub 32 metry są dłuższe niż 7 metrów. Ale jeśli chodzi o nieskończoność, nie można powiedzieć, że ta nieskończoność jest większa, mniejsza lub równa tej.”
To było rozwiązanie Galileusza 1600s.
Niestety, rozwiązanie Galileusza rozpoczęło nową debatę na temat nieskończoności. Matematycy i filozofowie nie mogli zgodzić się na konkretną odpowiedź, dopóki Cantor nie przedstawił swojej „teorii zbiorów”, której uczniowie uczą się dziś w szkole podstawowej.
Możemy okresowo uhistorycznić rozwój idei nieskończoności. Po raz pierwszy pojawiła się ona u Eleatów, którzy byli przedsokratejską szkołą filozoficzną założoną przez Parmenidesa na początku V wieku p.n.e. w starożytnym mieście Elea. W szkole tej działało trzech wielkich filozofów, takich jak Zeno, Ksenofanes i Parmenides. W tej szkole, przyjęta filozofia była taka, że istnienie było pojedyncze, i nie było wielości. Zenon był znany z paradoksów na temat nieskończoności u Eleatów. Później w 300 r. p.n.e., Arystoteles powstał i zaproponował parę pojęć, aby wyjaśnić paradoksy Zenona, które były potencjalną nieskończonością i rzeczywistą nieskończonością.
Potencjalna nieskończoność jest grupą liczb lub grupą „rzeczy”, która trwa bez zakończenia, kontynuując lub powtarzając się w kółko bez rozpoznawalnego punktu końcowego.
Faktyczna nieskończoność obejmuje nigdy niekończące się zestawy lub „rzeczy” w przestrzeni, która ma początek i koniec; jest to seria, która jest technicznie „zakończona”, ale składa się z nieskończonej liczby członków.
Arystoteles wierzył, że nie ma faktycznej nieskończoności. Ta idea Arystotelesa dominowała w świecie filozofii aż do lat 1600. Następnie filozofowie tacy jak Cusa i Bruno twierdzili, że istnieje rzeczywista nieskończoność, ale nie możemy nadać jej sensu. Po Cusie i Bruno, wielki myśliciel Spinoza włączył się do tematu.
Spinoza powiedział, że możemy zrozumieć pojęcie nieskończoności i uszeregować je pod względem wielkości. Jednak stwierdził również, że nie może zrobić matematyki na nich. Na przykład, mógł dodać 3 do 5, ale nie mógł dodać jednej nieskończoności do drugiej.
W końcu, aby zakończyć te debaty, pojawił się piękny człowiek, Georg Cantor i znalazł teorię zbiorów, która nadal jest podstawą matematyki. To on wyznaczył ostateczny punkt w dyskusjach o nieskończoności dzięki swojej teorii zbiorów.
Wykazał nam, że zbiór nieskończony będzie większy lub mniejszy od innego zbioru nieskończonego. Co więcej, Cantor twierdził, że możemy dodawać i mnożyć zbiory nieskończoności. Do tego czasu ludzie kierowali się ideami Arystotelesa na temat nieskończoności. Według Arystotelesa, gdybyśmy pomnożyli liczbę 3 przez nieskończoność, byłaby ona znowu nieskończona. Nieskończoność pochłonęłaby wszystko. Na tej podstawie twierdził, że istniałaby tylko potencjalna nieskończoność, a nie rzeczywista nieskończoność.
Jednakże Cantor udowodnił nam przeciwieństwo idei Arystotelesa za pomocą teorii zbiorów. Jeśli dodamy jeden do nieskończonego zbioru, to nie będzie to już ten sam zbiór. Próbował porównywać nieskończoności. Na przykład Cantor udowodnił, że zbiór wszystkich funkcji z (0,1)→ℕ jest policzalny. Zdefiniował więc funkcję jedno- i onto z przedziału (0,1) na liczby naturalne.
Innymi słowy, udowodnił, że wszystkie liczby naturalne mieszczą się między 0 a 1, ponieważ między 0-1 było nieskończenie wiele liczb racjonalnych, a te nieskończoności można sparować. Następnie zrobił coś jeszcze bardziej niebezpiecznego niż znalezienie dwóch równych nieskończoności. Porównał nieskończoność liczb rzeczywistych z nieskończonością liczb naturalnych i stwierdził, że nieskończoność liczb rzeczywistych jest większa od drugiej. Spojrzał nawet na swój dowód i powiedział swojemu przyjacielowi Dedekindowi: „Widzę to, ale nawet ja nie mogę w to uwierzyć …”.
Cantor był również matematykiem z bardzo poważnymi problemami filozoficznymi i religijnymi. Podczas opracowywania teorii zbiorów powiedział: „Bóg podyktował mi teorię zbiorów”.
Teoria zbiorów nie była powszechnie akceptowana, gdy została po raz pierwszy opracowana. Firmy nawet nie zatrudniały Cantora do żadnej pracy. Matematyk, Henri Poincaré, powiedział kiedyś: „Idee tego Cantora to zła choroba, która wbija się w kołnierz matematyki. I matematyka pewnego dnia go wyleczy”. Cantor musiał na jakiś czas trafić do szpitala psychiatrycznego i tam zmarł. Ale dziś uważamy go za geniusza.
Cantor był samotnym człowiekiem na skraju nieskończoności. Na początku swojego artykułu o liczbach nieskończonych zacytował Biblię: „Wszystko, co jest ukryte, zostanie wydobyte na światło dzienne”
.