Wartości własne macierzy to specjalny zbiór skalarów związanych z liniowym układem równań (tj.e., Równania macierzowe), które czasami są również znane jako korzenie charakterystyczne, wartości charakterystyczne (Hoffman i Kunze 1971), wartości właściwe lub korzenie ukryte (Marcus i Minc 1988, s. 144).

Wyznaczanie wartości własnych i wektorów własnych układu jest niezwykle ważne w fizyce i inżynierii, gdzie jest równoważne diagonalizacji macierzy i pojawia się w tak powszechnych zastosowaniach jak analiza stabilności, fizyka ciał wirujących i małe drgania systemów wibracyjnych, aby wymienić tylko kilka. Każda wartość własna jest sparowana z odpowiadającym jej tzw. wektorem własnym (lub, ogólnie, odpowiadającym jej prawym wektorem własnym i odpowiadającym jej lewym wektorem własnym; nie ma analogicznego rozróżnienia między lewą i prawą stroną dla wartości własnych).

Rozkład macierzy kwadratowej na wartości własne i wektory własne jest znany w tej pracy jako rozkład własny, a fakt, że rozkład ten jest zawsze możliwy, o ile macierz składająca się z wektorów własnych jest kwadratowa, jest znany jako twierdzenie o rozkładzie własnym.

Algorytm Lanczosa jest algorytmem obliczania wartości własnych i wektorów własnych dla dużych symetrycznych macierzy rzadkich.

Niech będzie przekształceniem liniowym reprezentowanym przez macierz . Jeśli istnieje wektor taki, że

(1)

dla pewnego skalara , to nazywamy wartością własną z odpowiadającym jej (prawym) wektorem własnym .

Letting be a square matrix

(2)

with eigenvalue , to odpowiadające im wektory własne spełniają

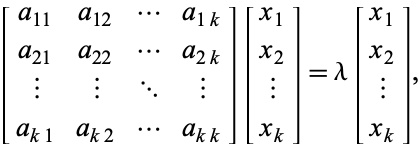(3)

co jest równoważne układowi jednorodnemu

.

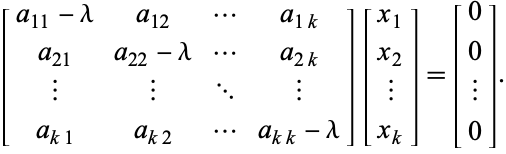(4)

Zapytanie (4) można zapisać zwięźle jako

(5)

gdzie jest macierzą tożsamości. Jak wynika z reguły Cramera, liniowy układ równań ma nietrywialne rozwiązania, jeśli wyznacznik znika, więc rozwiązania równania (5) są dane przez

(6)

Równanie to jest znane jako równanie charakterystyczne układu , a lewa strona jest znana jako wielomian charakterystyczny.

Na przykład, dla macierzy , wartości własne to

(7)

, które powstają jako rozwiązania równania charakterystycznego

(8)

Jeżeli wszystkie wartości własne są różne, to podłączenie ich z powrotem daje niezależnych równań dla składowych każdego odpowiadającego im wektora własnego, a system mówi się, że jest niezdegenerowany. Jeżeli wartości własne są -krotnie zdegenerowane, to mówi się, że układ jest zdegenerowany, a wektory własne nie są liniowo niezależne. W takich przypadkach, dodatkowe ograniczenie, aby wektory własne były ortogonalne,

(9)

gdzie jest deltą Kroneckera, może być zastosowane w celu uzyskania dodatkowych ograniczeń, umożliwiając w ten sposób rozwiązanie dla wektorów własnych.

Wartości własne mogą być obliczane w języku Wolfram Language za pomocą Eigenvalues. Wektory własne i wartości własne mogą być zwrócone razem za pomocą polecenia Eigensystem.

Zakładamy, że znamy wartość własną dla

(10)

Dodanie stałej razy macierz tożsamości do ,

(11)

więc nowe wartości własne są równe starym plus . Mnożąc przez stałą

(12)

więc nowe wartości własne są równe starym pomnożonym przez .

Teraz rozważmy przekształcenie podobieństwa . Niech będzie wyznacznikiem , wtedy

.

			(13)
			(14)
			(15)

więc wartości własne są takie same jak dla .