Wyobraź sobie kwadrat papieru leżący płasko na biurku. Proszę cię, abyś zamknął oczy. Słyszysz jak papier się przesuwa. Kiedy otwierasz oczy, wydaje się, że papier się nie zmienił. Co mogłem z nim zrobić, gdy nie patrzyłeś?
Jest oczywiste, że nie obróciłem papieru o 30 stopni, ponieważ wtedy papier wyglądałby inaczej.

Nie odwróciłem go również w poprzek linii łączącej, powiedzmy, jeden z rogów z punktem środkowym innej krawędzi. Papier wyglądałby inaczej, gdybym to zrobił.

Mogłem jednak obrócić papier zgodnie z ruchem wskazówek zegara lub przeciwnie do ruchu wskazówek zegara o dowolną wielokrotność 90 stopni lub przerzucić go w poprzek jednej z linii ukośnych lub linii poziomych i pionowych.
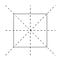
Pomocnym sposobem wizualizacji przekształceń jest zaznaczenie narożników kwadratu.

Ostatnią opcją jest nie robienie nic. Nazywa się to transformacją tożsamościową. Razem, to wszystko są nazywane przekształcenia symetrii kwadratu.
Mogę połączyć przekształcenia symetrii, aby inne przekształcenia symetrii. Na przykład, dwa przerzucenia przez odcinek linii BD dają identyczność, podobnie jak cztery kolejne obroty o 90 stopni w kierunku przeciwnym do ruchu wskazówek zegara. Przerzucenie o linię pionową, a następnie o linię poziomą daje taki sam efekt jak obrót o 180 stopni. Ogólnie rzecz biorąc, dowolna kombinacja przekształceń symetrii da przekształcenie symetrii. Poniższa tabela podaje reguły komponowania przekształceń symetrycznych:

W tej tabeli R z indeksami 90, 180 i 270 oznaczają obrót o 90, 180 i 270 stopni w kierunku przeciwnym do ruchu wskazówek zegara, H oznacza obrót wokół linii poziomej, V – obrót wokół linii pionowej, MD – obrót wokół przekątnej od lewej górnej do prawej dolnej, a OD – obrót wokół drugiej przekątnej. Aby znaleźć iloczyn A i B, przejdź do wiersza A, a następnie do kolumny B. Na przykład H∘MD=R₉₀.
Jest kilka rzeczy, które możesz zauważyć, patrząc na tabelę:
- Operacja ∘ jest asocjacyjna, co oznacza, że A∘(B∘C) = (A∘B)∘C dla dowolnych przekształceń A, B i C.
- Dla dowolnej pary przekształceń symetrycznych A i B, kompozycja A∘B jest również przekształceniem symetrycznym
- Istnieje jeden element e taki, że A∘e=e∘A dla każdego A
- Dla każdego przekształcenia symetrycznego A, istnieje unikalne przekształcenie symetrii A-¹ takie, że A∘A-¹=A-¹∘A=e
Mówimy zatem, że zbiór przekształceń symetrii kwadratu, w połączeniu ze składem, tworzy strukturę matematyczną zwaną grupą. Grupę tę nazywamy D₄, czyli grupą diadyczną dla kwadratu. Struktury te są przedmiotem tego artykułu.
Definicja grupy
Grupa ⟨G,*⟩ to zbiór G z regułą * łączenia dowolnych dwóch elementów w G, która spełnia aksjomaty grupy:
W abstrakcji często tłumimy * i piszemy a*b jako ab oraz odnosimy się do * jako mnożenia.

Nie jest konieczne, aby * było komutatywne, co oznacza, że a*b=b*a. Można się o tym przekonać, patrząc na tablicę D₄, gdzie H∘MD=R₉₀, ale MD∘H=R₂₇₀. Grupy, w których * jest komutatywne nazywane są grupami abelowskimi po Neils Abel.
Grupy abelowskie są raczej wyjątkiem niż regułą. Innym przykładem grupy nieabelowej są przekształcenia symetrii sześcianu. Rozważmy tylko obroty wokół osi:
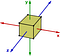
Jeśli najpierw obrócę się o 90 stopni przeciwnie do ruchu wskazówek zegara wokół osi y, a następnie o 90 stopni przeciwnie do ruchu wskazówek zegara wokół osi z, to jego będzie miał inny wynik niż gdybym obrócił się o 90 stopni wokół osi z, a następnie o 90 stopni wokół osi y.

Możliwe jest, aby element był swoim własnym odwrotnością. Rozważmy grupę, która składa się z 0 i 1 z operacją dodawania binarnego. Jej tablica to:

Wyraźnie 1 jest swoim własnym odwrotnością. Jest to również grupa abeliczna. Nie martw się, większość grup nie jest tak nudna.
Kilka innych przykładów grup to:
- Zbiór liczb całkowitych z dodawaniem.
- Zbiór liczb racjonalnych nie zawierających 0 z mnożeniem.
- Zbiór rozwiązań równania wielomianowego xⁿ-1=0, zwanych n-tymi korzeniami jedności, z mnożeniem.
Oto kilka przykładów, które nie są grupami:
- Zbiór liczb naturalnych w dodawaniu nie jest grupą, bo nie ma odwrotności, którymi byłyby liczby ujemne.
- Zbiór wszystkich liczb racjonalnych, w tym 0 z mnożeniem nie jest grupą, ponieważ nie ma liczby racjonalnej q, dla której 0/q=1, więc nie każdy element ma odwrotność.
Struktura grupy
Grupa jest czymś więcej niż tylko plamką, która spełnia cztery aksjomaty. Grupa może mieć wewnętrzną strukturę, a ta struktura może być bardzo zawiła. Jednym z podstawowych problemów w algebrze abstrakcyjnej jest określenie, jak wygląda wewnętrzna struktura grupy, ponieważ w rzeczywistym świecie grupy, które są faktycznie badane, są znacznie większe i bardziej skomplikowane niż proste przykłady, które tu podaliśmy.
Jednym z podstawowych typów struktury wewnętrznej jest podgrupa. Grupa G ma podgrupę H, gdy H jest podzbiorem G i:
- Dla a,b∈H, a*b∈H i b*a∈H
- Dla a∈H, a-¹∈H
- Tożsamość jest elementem H
Jeśli H≠G to mówi się, że H jest podgrupą właściwą. Podgrupa G składająca się tylko z tożsamości nazywana jest podgrupą trywialną.
Grupa nieabelowa może mieć podgrupy komutatywne. Rozważmy kwadratową grupę katedralną, którą omawialiśmy we wstępie. Grupa ta nie jest abelianem, ale podgrupa rotacji jest abelianem i jest cykliczna:
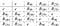
Podamy teraz dwa przykłady struktury grupy.
Nawet jeśli grupa G nie jest abelianem, może się zdarzyć, że istnieje zbiór elementów G, które komutują ze wszystkim w G. Zbiór ten nazywamy centrum G. Środek C jest podgrupą grupy G. Dowód:
Załóżmy teraz, że f jest funkcją, której dziedziną i zakresem jest zarówno G. Okresem f jest element a∈G taki, że f(x)=f(ax) dla wszystkich x∈G. Zbiór P okresów f jest podgrupą G. Dowód:
Grupy skończone są skończenie generowane
Widzieliśmy, że grupy cykliczne są generowane przez jeden element. Jeśli każdy element grupy G można zapisać jako iloczyn (niekoniecznie właściwego) podzbioru A grupy G, to mówimy, że A generuje G i zapisujemy to jako G=⟨A⟩. Najbardziej „no tak, duh” dowód jaki kiedykolwiek zobaczysz to dowód na to, że wszystkie grupy skończone są generowane przez skończony zbiór generujący:
- Niech G będzie skończone. Każdy element G jest iloczynem dwóch innych elementów G, więc G=⟨G⟩. QED.

Zakończymy ten artykuł pewnym zastosowaniem.
Komunikacja odporna na błędy
Najprostszym sposobem przesyłania informacji cyfrowej jest kodowanie jej w ciągach binarnych o stałej długości. Żaden schemat komunikacji nie jest całkowicie wolny od zakłóceń, więc zawsze istnieje możliwość, że zostaną odebrane błędne dane. Metoda dekodowania z maksymalnym prawdopodobieństwem jest prostym i skutecznym podejściem do wykrywania i korygowania błędów transmisji.
Pozwól 𝔹ⁿ być zbiorem ciągów binarnych, lub słów, o długości n. Łatwo pokazać, że 𝔹ⁿ jest grupą abelianów pod dodawaniem binarnym bez przenoszenia (tak, że na przykład 010+011=001). Zauważmy, że każdy element jest swoim własnym odwrotnością. Kod C jest podzbiorem 𝔹ⁿ. Poniżej podano przykład kodu w 𝔹⁶:
C = {0000, 001011, 010110, 011101, 100101, 101110, 110011, 111000}
Elementy kodu nazywamy słowami kodowymi. Tylko słowa kodowe będą przesyłane. O błędzie mówimy, gdy zakłócenia zmieniają bit w przesyłanym słowie. Odległość d(a,b) między dwoma słowami kodowymi a i b jest to liczba cyfr, którymi różnią się dwa słowa kodowe. Minimalna odległość kodu to najmniejsza odległość między dowolnymi dwoma jego słowami kodowymi. Dla powyższego przykładowego kodu minimalna odległość wynosi trzy.
W metodzie dekodowania z maksymalnym prawdopodobieństwem, jeśli otrzymujemy słowo x, które może zawierać błędy, odbiorca powinien zinterpretować x jako słowo kodowe a takie, że d(a,x) jest minimalne. Pokażę, że dla kodu o minimalnej odległości m można zawsze (1) wykryć błędy, które zmieniają mniej niż m bitów i (2) poprawić błędy, które zmieniają ½(m-1) lub mniej bitów.

W naszym przykładowym kodzie, m=3 i sfera o promieniu ½(m-1)=1 wokół słowa kodowego 011101 to {011101, 111101, 001101, 011001, 010101, 011111, 011100}. Więc jeśli odbiornik otrzyma którekolwiek z tych słów, wie, że miał otrzymać 011101.
Więc to wszystko dobrze, ale co to ma wspólnego z teorią grup? Odpowiedź tkwi w tym, jak faktycznie tworzymy kody, z którymi pracuje ta metoda.
Możliwe jest, aby kod w 𝔹ⁿ tworzył podgrupę. W takim przypadku mówimy, że kod jest kodem grupowym. Kody grupowe są grupami skończonymi, więc są skończenie generowane. Zobaczymy jak stworzyć kod poprzez znalezienie zbioru generującego.
Kod może być określony tak, że kilka pierwszych bitów każdego słowa kodowego jest nazywanych bitami informacji, a bity na końcu są nazywane bitami parzystości. W naszym przykładowym kodzie C, pierwsze trzy bity są bitami informacji, a ostatnie trzy są bitami parzystości. Bity parzystości spełniają równania kontroli parzystości. Dla słowa kodowego A₁A₂A₃A₄A₅A₆ równania parzystości mają postać A₄=A₁+A₂, A₅=A₂+A₃ oraz A₆=A₁+A₃. Równania parzystości zapewniają kolejną warstwę ochrony przed błędami: jeśli którekolwiek z równań parzystości nie jest spełnione, to wystąpił błąd.
Oto, co robimy. Załóżmy, że chcemy mieć słowa kodowe z m bitami informacji i n bitami parzystości. Aby wygenerować kod grupowy, należy napisać macierz o m wierszach i m+n kolumnach. W bloku utworzonym przez pierwsze m kolumn wpisujemy macierz tożsamości m×m. W kolumnie j dla m+1≤j≤m_n należy wpisać 1 w k-tym wierszu, jeśli Aₖ występuje w równaniu parzystości dla bitu parzystości Aⱼ i 0 w przeciwnym przypadku. W naszym przykładowym kodzie macierz ma postać:

Macierz taką nazywamy macierzą generującą dla kodu grupowego. Można sprawdzić bezpośrednio, że wiersze generują C:

Rowery dowolnej macierzy generującej tworzą zbiór generujący dla kodu grupowego C. Dowód:
- Tożsamość i odwrotności: Każdy wiersz dodany do siebie daje tożsamość, ciąg składający się ze wszystkich zer.
- Zamknięcie: Jeśli A,B∈C to A i B są sumami wierszy macierzy generującej, więc A+B jest również sumą wierszy macierzy generującej. Zatem A+B∈C.
To pozwala nam wygenerować kod, teraz pokażę jak wygenerować użyteczny kod.
Zdefiniuj wagę w(x) jako liczbę jedynek w x. Na przykład, w(100101)=3. Jest oczywiste, że w(x)=d(x,0) gdzie 0 jest słowem, którego wszystkie cyfry są zerami. Minimalna waga W kodu to waga niezerowego słowa kodowego o najmniejszej liczbie jedynek w kodzie. Dla kodu o minimalnej odległości m, d(x,0)≥m więc w(x)≥m i dlatego W=m.
Przypomnijmy, że aby słowo mogło być uznane za słowo kodowe, musi spełniać zestaw równań kontroli parzystości. Dla naszego przykładowego kodu są to A₄=A₁+A₂, A₅=A₂+A₃ oraz A₆=A₁+A₃. Możemy je również zapisać w postaci układu liniowego:
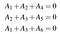
Który sam można zapisać w postaci iloczynów kropkowych:

Albo w bardziej zwartej formie jako Ha=0 gdzie a=(A₁,A₂,A₃,A₄,A₅,A₆), a H jest macierzą kontroli parzystości dla kodu:

Można sprawdzić przez bezpośrednie obliczenia, że jeśli w(a)≤2 to nie możemy mieć Ha=0. W ogólności minimalna waga to t+1, gdzie t jest najmniejszą liczbą taką, że dowolny zbiór t kolumn H nie sumuje się do zera (tzn. są one liniowo niezależne). Udowodnienie tego zabrałoby nas tylko trochę za daleko w algebrę liniową.
Jeśli to cię przeraża, nie martw się. Możemy wyprodukować kilka bardzo dobrych kodów bez tego, wykorzystując fakt, że wynik, o którym właśnie wspomniałem, implikuje, że jeśli każda kolumna H jest niezerowa i żadne dwie kolumny nie są równe, to minimalna waga, a więc i minimalna odległość kodu, wynosi co najmniej trzy. To bardzo dobrze: Jeśli nasz system komunikacyjny ma mieć jeden błąd bitowy na każde sto transmitowanych słów, to tylko jedno na dziesięć tysięcy transmitowanych słów będzie miało nieskorygowany błąd, a jedno na milion transmitowanych słów będzie miało niewykryty błąd.
Mamy więc teraz przepis na wyprodukowanie użytecznego kodu dla schematu detekcji z maksymalnym prawdopodobieństwem dla słów kodowych zawierających m bitów informacji i n bitów parzystości:
- Stwórz macierz o m+n kolumnach i n wierszach. Wypełnij macierz jedynkami i zerami tak, aby żadne dwie kolumny nie były takie same i żadna kolumna nie była tylko zerami.
- Każdy wiersz wynikowej macierzy kontroli parzystości odpowiada jednemu z równań bitów parzystości. Zapisz je jako układ równań i rozwiąż tak, aby każdy bit parzystości był zapisany w postaci bitów informacji.
- Utwórz macierz o m+n kolumnach i m wierszach. W bloku utworzonym przez pierwsze m kolumn zapisz macierz tożsamości m×m. W kolumnie j dla m+1≤j≤m_n, napisz 1 w k-tym wierszu, jeśli Aₖ pojawia się w równaniu parzystości dla bitu parzystości Aⱼ i 0 w przeciwnym razie.
- Rowery tej macierzy są generatorami grupy kodowej z minimalną odległością co najmniej trzy. To jest kod, którego będziemy używać.
Jako przykład, załóżmy, że potrzebuję prostego, ośmiosłownego kodu i potrzebuję tylko podstawowej detekcji błędów, a nie korekcji, więc mogę uciec z minimalną odległością dwóch. Chcę mieć trzy bity informacyjne i dwa bity parzystości. Zapisuję następującą macierz kontroli parzystości:
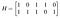
Dwie pary kolumn są równe, więc najmniejsze t, dla którego dowolny zbiór t kolumn jest liniowo niezależny, wynosi jeden, więc minimalna waga, a zatem minimalna odległość, którą będę miał, wynosi dwa. Wiersze reprezentują równania kontroli parzystości A₄=A₁+A₃ oraz A₅=A₁+A₂+A₃. Moja macierz generująca to zatem:

A wiersze tej macierzy generują grupę kodów:
- {00000, 00111, 01001, 01110, 10011, 10100, 111010, 11101}
Uwagi końcowe
Algebra abstrakcyjna jest głębokim tematem o dalekosiężnych implikacjach, ale jest też bardzo łatwa do nauczenia. Poza kilkoma wzmiankami o algebrze liniowej, prawie wszystko, co tutaj omówiłem, jest dostępne dla kogoś, kto miał tylko algebrę w szkole średniej.
Kiedy po raz pierwszy wpadłem na pomysł napisania tego artykułu, naprawdę chciałem porozmawiać o kostce Rubika, ale w końcu chciałem wybrać przykład, który może być pokryty tylko z najbardziej podstawowymi ideami teorii grup. Dodatkowo, jest tak wiele do powiedzenia o grupie kostki Rubika, że zasługuje ona na samodzielny artykuł, który pojawi się wkrótce.
Kursy algebry abstrakcyjnej w moim college’u były oparte na książce A Book of Abstract Algebra autorstwa Charlesa Pintera, która jest przystępnie napisana. Przykłady w tym artykule zostały zapożyczone z pewnymi modyfikacjami od Pintera.
Jako ostatnia uwaga, wszelkie obrazy, które nie są cytowane są moją własną oryginalną pracą i mogą być używane z atrybucją. Jak zawsze, doceniam wszelkie korekty lub prośby o wyjaśnienie.