A sajátértékek egy lineáris egyenletrendszerhez tartozó skalárok speciális halmaza (i.e., egy mátrixegyenlethez), amelyeket néha karakterisztikus gyököknek, jellemző értékeknek (Hoffman és Kunze 1971), sajátértékeknek vagy látens gyököknek is neveznek (Marcus és Minc 1988, 144. o.).

A rendszer sajátértékeinek és sajátvektorainak meghatározása rendkívül fontos a fizikában és a mérnöki tudományokban, ahol ez egyenértékű a mátrixdiagonalizációval, és olyan gyakori alkalmazásokban merül fel, mint a stabilitáselemzés, a forgó testek fizikája és a rezgő rendszerek kis rezgései, hogy csak néhányat említsünk. Minden egyes sajátértékhez párosul egy megfelelő, úgynevezett sajátvektor (vagy általában egy megfelelő jobb sajátvektor és egy megfelelő bal sajátvektor; a sajátértékek esetében nincs analóg megkülönböztetés a bal és a jobb oldal között).

A négyzetes mátrix sajátértékekre és sajátvektorokra való felbontását ebben a munkában sajátérték-felbontásnak nevezzük, és azt a tényt, hogy ez a felbontás mindig lehetséges, amíg a sajátvektoraiból álló mátrix négyzetes, sajátérték-felbontási tételként ismerjük.

A Lanczos-algoritmus egy algoritmus nagy szimmetrikus ritka mátrixok sajátértékeinek és sajátvektorainak kiszámítására.

Legyen egy mátrix által reprezentált lineáris transzformáció. Ha van olyan vektor, hogy

(1)

valamilyen skalárra, akkor a sajátértékének nevezzük, amelynek megfelelő (jobb) sajátvektora .

Legyen egy négyzetes mátrix

(2)

sajátértékkel , akkor a megfelelő sajátvektorok kielégítik

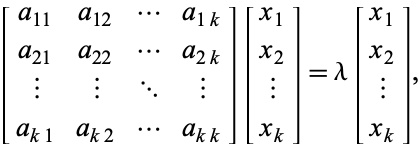(3)

, ami egyenértékű a homogén rendszerrel

.

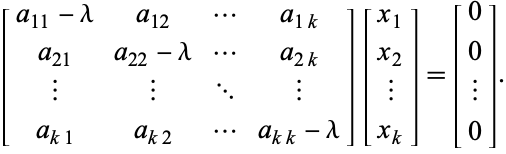(4)

A (4) egyenlet kompakt módon felírható

(5)

ahol az azonossági mátrix. A Cramer-szabály szerint egy lineáris egyenletrendszernek akkor vannak nemtriviális megoldásai, ha a determináns eltűnik, tehát az (5. egyenlet megoldásai a következők:

(6)

Ezt az egyenletet karakterisztikus egyenletének, baloldali oldalát pedig karakterisztikus polinomnak nevezzük.

Például egy mátrix esetében, a sajátértékek a következők

(7)

, amelyek a következő megoldásokként keletkeznek karakterisztikus egyenlet

(8)

Ha minden sajátérték különböző, akkor ezeket visszadugva független egyenletet kapunk minden egyes megfelelő sajátvektor komponensére, és a rendszerről azt mondjuk, hogy nem degenerált. Ha a sajátértékek -szeresen degeneráltak, akkor a rendszert degeneráltnak mondjuk, és a sajátvektorok nem lineárisan függetlenek. Ilyen esetekben az a további kényszer, hogy a sajátvektorok ortogonálisak legyenek,

(9)

ahol a Kronecker-delta, alkalmazható, hogy további kényszereket kapjunk, így lehetővé válik a sajátvektorok megoldása.

A sajátértékek kiszámíthatók a Wolfram Nyelvben a Sajátértékek segítségével. A sajátvektorok és a sajátértékek együttesen is visszaadhatók az Eigensystem paranccsal.

Tegyük fel, hogy ismerjük a

(10)

Az sajátértékét, ha egy konstans szorozva az azonossági mátrixot adjuk hozzá,

(11)

így az új sajátértékek megegyeznek a régivel plusz . megszorozva

(12)

szóval az új sajátértékek a régi és szorozva

Most tekintsük a hasonlósági transzformációját. Legyen a determinánsa, akkor

.

			(13)
			(14)
			(15)

tehát a sajátértékek ugyanazok, mint a esetében.