Lärandemål
- Känna till förhållandet mellan syra- eller basstyrka och storleken på \(K_a\), \(K_b\), \(pK_a\) och \(pK_b\).
- För att förstå utjämningseffekten.
Storleken på jämviktskonstanten för en joniseringsreaktion kan användas för att bestämma den relativa styrkan hos syror och baser. Den allmänna ekvationen för joniseringen av en svag syra i vatten, där HA är modersyran och A- är dess konjugerade bas, är till exempel följande:
\
Jämviktskonstanten för denna dissociation är följande:
\}{} \label{16.5.2}\]
Som vi noterade tidigare är koncentrationen av vatten i stort sett konstant för alla reaktioner i vattenlösning, så \(\) i ekvation \(\ref{16.5.2}\) kan införlivas i en ny kvantitet, syrajoniseringskonstanten (\(K_a\)), som också kallas för syradissociationskonstanten:
\=\dfrac{}{}{} \label{16.5.3}\]
Därmed skiljer sig de numeriska värdena för K och \(K_a\) åt genom koncentrationen av vatten (55,3 M). För enkelhetens skull kan \(H_3O^+\) skrivas som \(H^+\) i ekvation \(\ref{16.5.3}\). Kom dock ihåg att fri \(H^+\) inte existerar i vattenlösningar och att en proton överförs till \(H_2O\) i alla syrajoniseringsreaktioner för att bilda hydroniumjoner, \(H_3O^+\). Ju större \(K_a\), desto starkare är syran och desto högre är koncentrationen av \(H^+\) vid jämvikt. Liksom alla jämviktskonstanter mäts syra-basjoniseringskonstanter faktiskt i termer av aktiviteterna av \(H^+\) eller \(OH^-\), vilket gör dem enhetslösa. Värdena för \(K_a\) för ett antal vanliga syror anges i tabell \(\PageIndex{1}\).
Svaga baser reagerar med vatten för att producera hydroxidjonen enligt följande allmänna ekvation, där B är moderbasen och BH+ är dess konjugerade syra:
\
Jämviktskonstanten för denna reaktion är basjoniseringskonstanten (Kb), som också kallas basdissociationskonstanten:
\= \frac{}{} \label{16.5.5}\]
Ännu en gång är koncentrationen av vatten konstant, så den förekommer inte i uttrycket för jämviktskonstanten; istället ingår den i \(K_b\). Ju större \(K_b\), desto starkare är basen och desto högre är \(OH^-\)-koncentrationen vid jämvikt. Värdena för \(K_b\) för ett antal vanliga svaga baser anges i tabell \(\PageIndex{2}\).
Det finns ett enkelt samband mellan storleken på \(K_a\) för en syra och \(K_b\) för dess konjugerade bas. Tänk till exempel på joniseringen av cyanvätesyra (\(HCN\)) i vatten för att producera en sur lösning, och reaktionen av \(CN^-\) med vatten för att producera en basisk lösning:
\
\
\
Gjämviktskonstantuttrycket för joniseringen av HCN är som följer:
\}{} \label{16.5.8}\]
Det motsvarande uttrycket för cyanidens reaktion med vatten är följande:
\}{} \label{16.5.9}\]
Om vi lägger till ekvationerna \(\ref{16.5.6}\) och \(\ref{16.5.7}\) får vi följande:
| Reaktion | Gjämviktskonstanter |
|---|---|
| \(\cancel{HCN_{(aq)}} \rightleftharpoons H^+_{(aq)}+\cancel{CN^-_{(aq)}} \) | \(K_a=\cancel{}/\cancel{}\) |
| \(\cancel{CN^-_{(aq)}}+H_2O_{(l)} \rightleftharpoons OH^-_{(aq)}+\cancel{HCN_{(aq)}}}\) | \(K_b=\cancel{}/\cancel{}\) |
| \(H_2O_{(l)} \rightleftharpoons H^+_{(aq)}+OH^-_{(aq)}\) | \(K=K_a \times K_b=\) |
I detta fall, är summan av de reaktioner som beskrivs av \(K_a\) och \(K_b\) ekvationen för autojonisering av vatten, och produkten av de två jämviktskonstanterna är \(K_w\):
\
Om vi känner till antingen \(K_a\) för en syra eller \(K_b\) för dess konjugerade bas kan vi alltså beräkna den andra jämviktskonstanten för varje konjugerat syra-baspar.
Som med \(pH\), \(pOH\) och pKw kan vi använda negativa logaritmer för att undvika exponentiell notation när vi skriver joniseringskonstanter för syror och baser, genom att definiera \(pK_a\) på följande sätt:
\
\
och \(pK_b\) som
\
\
\
Samma gäller ekvation \(\ref{16.5.10}\), som uttrycker förhållandet mellan \(K_a\) och \(K_b\), kan skrivas i logaritmisk form enligt följande:
\
Vid 25 °C blir detta
\
Värdena för \(pK_a\) och \(pK_b\) anges för flera vanliga syror och baser i tabellerna \(\PageIndex{1}\) och \(\PageIndex{2}\), och en mer omfattande uppsättning data finns i tabellerna E1 och E2. På grund av användningen av negativa logaritmer motsvarar mindre värden på \(pK_a\) större syrajoniseringskonstanter och därmed starkare syror. Nitrös syra (\(HNO_2\)), med en \(pK_a\) på 3,25, är t.ex. ungefär en miljon gånger starkare syra än cyanvätesyra (HCN), med en \(pK_a\) på 9,21. Omvänt motsvarar mindre värden på \(pK_b\) större basjoniseringskonstanter och därmed starkare baser.
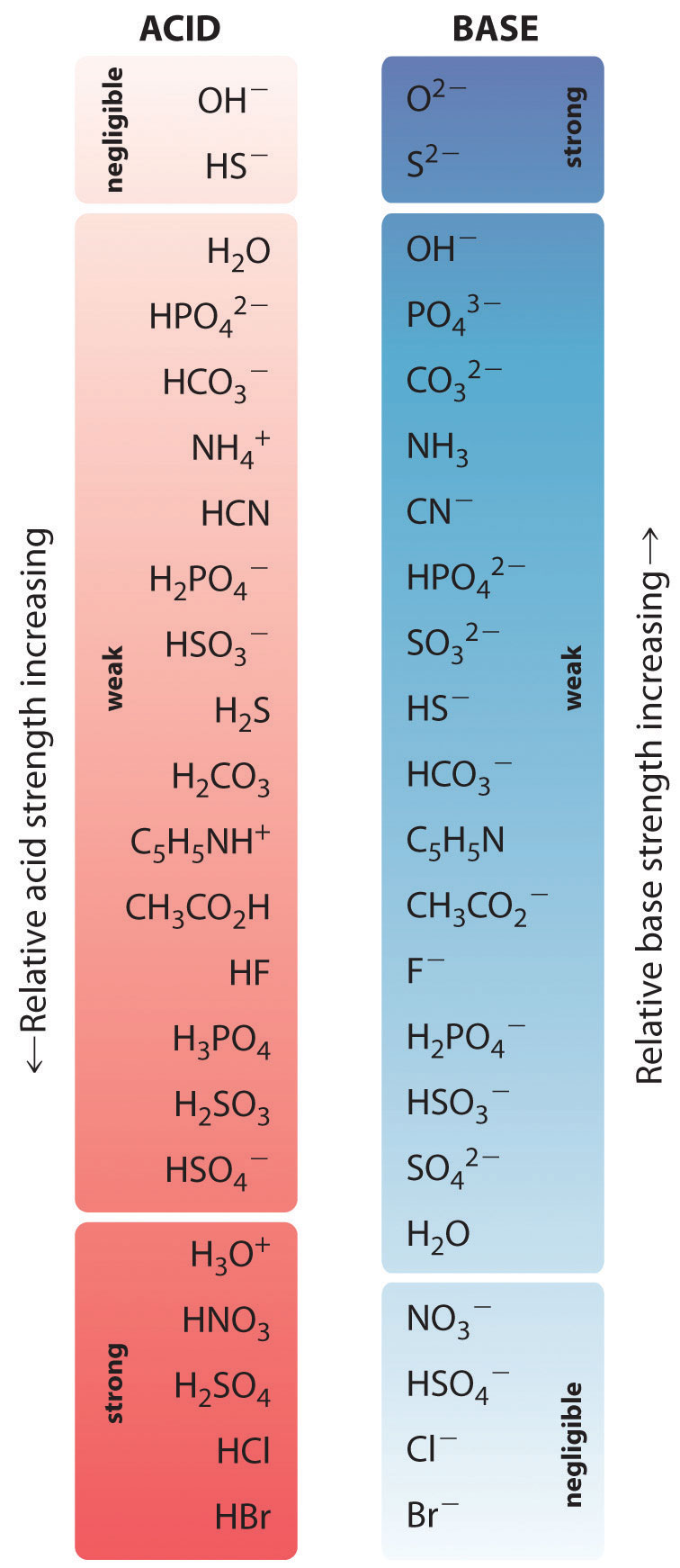
Den relativa styrkan hos några vanliga syror och deras konjugerade baser visas grafiskt i figur \(\PageIndex{1}\). De konjugerade syra-bas-paren är listade i ordning (uppifrån och ner) med ökande syrastyrka, vilket motsvarar minskande värden på \(pK_a\). Denna ordning motsvarar minskande styrka hos den konjugerade basen eller ökande värden på \(pK_b\). Längst ner till vänster i figur \(\PageIndex{2}\) finns de vanligaste starka syrorna och längst upp till höger de vanligaste starka baserna. Lägg märke till det omvända förhållandet mellan styrkan hos modersyran och styrkan hos den konjugerade basen. Således är den konjugerade basen till en stark syra en mycket svag bas, och den konjugerade basen till en mycket svag syra är en stark bas.
Den konjugerade basen till en stark syra är en svag bas och vice versa.
Vi kan använda de relativa styrkorna hos syror och baser för att förutsäga riktningen på en syra-basreaktion genom att följa en enda regel: en syra-basjämvikt gynnar alltid sidan med den svagare syran och basen, vilket indikeras av dessa pilar:
\
I en syra-basreaktion reagerar protonen alltid med den starkare basen.
Saltsyran är till exempel en stark syra som joniserar i stort sett fullständigt i utspädd vattenlösning för att producera \(H_3O^+\) och \(Cl^-\); endast försumbara mängder \(HCl\)-molekyler förblir odissocierade. Därför ligger joniseringsjämvikten praktiskt taget hela vägen till höger, vilket representeras av en enda pil:
Däremot är ättiksyra en svag syra och vatten en svag bas. Följaktligen innehåller vattenlösningar av ättiksyra mestadels ättiksyramolekyler i jämvikt med en liten koncentration av \(H_3O^+\) och acetatjoner, och joniseringsjämvikten ligger långt till vänster, vilket representeras av dessa pilar:
\
Samma sak gäller för ammoniakens reaktion med vatten, där hydroxidjonen är en stark bas och ammoniak är en svag bas, medan ammoniumjonen är en starkare syra än vatten. Därför ligger även denna jämvikt till vänster:
\
Alla syra-basjämvikter gynnar sidan med den svagare syran och basen. Protonerna är alltså bundna till den starkare basen.
Exempel \(\PageIndex{1}\): Butyrat- och dimetylammoniumjoner
- Beräkna \(K_b\) och \(pK_b\) för butyratjonen (\(CH_3CH_2CH_2CO_2CO_2^-\)). \(pK_a\) för smörsyra vid 25 °C är 4,83. Butyrsyra är orsaken till den dåliga lukten av härsket smör.
- Beräkna \(K_a\) och \(pK_a\) för dimetylammoniumjonen (\((CH_3)_2NH_2^+\)). Basjoniseringskonstanten \(K_b\) för dimetylamin (\((CH_3)_2NH\)) är \(5,4 \ gånger 10^{-4}\) vid 25°C.
Givet: \(pK_a\) och \(K_b\)
Sökt efter: motsvarande \(K_b\) och \(pK_b\), \(K_a\) och \(pK_a\)
Strategi:
Konstanterna \(K_a\) och \(K_b\) är relaterade enligt ekvation \(\ref{16.5.10}\). Konstanterna \(pK_a\) och \(pK_b\) för en syra och dess konjugerade bas är relaterade enligt ekvationerna \(\ref{16.5.15}\) och \(\(\ref{16.5.16}\). Använd relationerna pK = -log K och K = 10-pK (ekvationerna \(\ref{16.5.11}\) och \(\ref{16.5.13}\)) för att konvertera mellan \(K_a\) och \(pK_a\) eller \(K_b\) och \(pK_b\).
Lösning:
Vi får \(pK_a\) för smörsyra och ombeds att beräkna \(K_b\) och \(pK_b\) för dess konjugerade bas, butyratjonen. Eftersom det angivna värdet för \(pK_a\) gäller för en temperatur på 25 °C kan vi använda ekvation \(\ref{16.5.16}\): \(pK_a\) + \(pK_b\) = pKw = 14,00. Genom att ersätta \(pK_a\) och lösa \(pK_b\),
\\
\
Eftersom \(pK_b = -\log K_b\) är \(K_b\) \(10^{-9,17} = 6,8 \ gånger 10^{-10}\).
I detta fall får vi \(K_b\) för en bas (dimetylamin) och ombeds att beräkna \(K_a\) och \(pK_a\) för dess konjugerade syra, dimetylammoniumjonen. Eftersom den ursprungliga kvantiteten är \(K_b\) snarare än \(pK_b\) kan vi använda ekvation \(\ref{16.5.10}\): \(K_aK_b = K_w\). Genom att ersätta värdena för \(K_b\) och \(K_w\) vid 25°C och lösa \(K_a\),
\
\
Eftersom \(pK_a\) = -log \(K_a\) har vi \(pK_a = -\log(1,9 \ gånger 10^{-11}) = 10,72\). Vi kunde också ha omvandlat \(K_b\) till \(pK_b\) för att få samma svar:
\
Om vi får någon av dessa fyra storheter för en syra eller en bas (\(K_a\), \(pK_a\), \(K_b\) eller \(pK_b\)) kan vi beräkna de andra tre.
Övning \(\PageIndex{1}\): Mjölksyra
Mjölksyra (\(CH_3CH(OH)CO_2H\)) är ansvarig för den starka smaken och lukten av surmjölk; den anses också ge ömhet i trötta muskler. Dess \(pK_a\) är 3,86 vid 25°C. Beräkna \(K_a\) för mjölksyra och \(pK_b\) och \(K_b\) för laktatjonen.
Svar
- \(K_a = 1,4 \ gånger 10^{-4}\) för mjölksyra;
- \(pK_b\) = 10.14 och
- \(K_b = 7,2 \times 10^{-11}\) för laktatjonen
- Solutions of Strong Acids and Bases: Du kommer att märka i tabell \(\(\PageIndex{1}\) att syror som \(H_2SO_4\) och \(HNO_3\) ligger ovanför hydroniumjonen, vilket innebär att de har \(pK_a\)-värden som är mindre än noll och är starkare syror än \(H_3O^+\)-jonen. Kom ihåg från kapitel 4 att den sura protonen i praktiskt taget alla oxosyror är bunden till en av syreatomerna i oxoanjonen. Salpetersyra bör därför korrekt skrivas som \(HONO_2\). Tyvärr skrivs dock formlerna för oxosyror nästan alltid med väte till vänster och syre till höger, vilket ger \(HNO_3\) i stället. Faktum är att alla sex vanliga starka syror som vi först stötte på i kapitel 4 har \(pK_a\)-värden som är lägre än noll, vilket innebär att de har en större tendens att förlora en proton än vad \(H_3O^+\)-jonen har. Omvänt är de konjugerade baserna till dessa starka syror svagare baser än vatten. Följaktligen ligger protonöverföringsjämvikten för dessa starka syror långt till höger, och tillsats av någon av de vanliga starka syrorna till vatten resulterar i en i huvudsak stökiometrisk reaktion av syran med vatten för att bilda en lösning av \(H_3O^+\)-jonen och syrans konjugerade bas.
- Polyprotiska syror och baser
- Sammanfattning
- Nyckelekvationer
- Kontributorer och tillskrivningar
Solutions of Strong Acids and Bases: Du kommer att märka i tabell \(\(\PageIndex{1}\) att syror som \(H_2SO_4\) och \(HNO_3\) ligger ovanför hydroniumjonen, vilket innebär att de har \(pK_a\)-värden som är mindre än noll och är starkare syror än \(H_3O^+\)-jonen. Kom ihåg från kapitel 4 att den sura protonen i praktiskt taget alla oxosyror är bunden till en av syreatomerna i oxoanjonen. Salpetersyra bör därför korrekt skrivas som \(HONO_2\). Tyvärr skrivs dock formlerna för oxosyror nästan alltid med väte till vänster och syre till höger, vilket ger \(HNO_3\) i stället. Faktum är att alla sex vanliga starka syror som vi först stötte på i kapitel 4 har \(pK_a\)-värden som är lägre än noll, vilket innebär att de har en större tendens att förlora en proton än vad \(H_3O^+\)-jonen har. Omvänt är de konjugerade baserna till dessa starka syror svagare baser än vatten. Följaktligen ligger protonöverföringsjämvikten för dessa starka syror långt till höger, och tillsats av någon av de vanliga starka syrorna till vatten resulterar i en i huvudsak stökiometrisk reaktion av syran med vatten för att bilda en lösning av \(H_3O^+\)-jonen och syrans konjugerade bas.
Och även om \(K_a\) för \(HI\) är ca 108 större än \(K_a\) för \(HNO_3\), ger reaktionen av antingen \(HI\) eller \(HNO_3\) med vatten en i stort sett stökiometrisk lösning av \(H_3O^+\) och I- eller \(NO_3^-\). Faktum är att en 0,1 M vattenlösning av en stark syra faktiskt innehåller 0,1 M \(H_3O^+\), oavsett vilken den starka syran är. Detta fenomen kallas utjämningseffekten: varje art som är en starkare syra än vattnets konjugerade syra (\(H_3O^+\)) utjämnas till styrkan hos \(H_3O^+\) i vattenlösning eftersom \(H_3O^+\) är den starkaste syra som kan existera i jämvikt med vatten. Följaktligen är det omöjligt att skilja mellan styrkan hos syror som HI och HNO3 i vattenlösning, och ett alternativt tillvägagångssätt måste användas för att bestämma deras relativa syrestyrka.
En metod är att använda ett lösningsmedel som vattenfri ättiksyra. Eftersom ättiksyra är en starkare syra än vatten måste den också vara en svagare bas, med en mindre tendens att acceptera en proton än \(H_2O\). Mätningar av konduktiviteten hos 0,1 M-lösningar av både HI och \(HNO_3\) i ättiksyra visar att HI är helt dissocierad, men \(HNO_3\) är endast delvis dissocierad och beter sig som en svag syra i detta lösningsmedel. Detta resultat visar tydligt att HI är en starkare syra än \(HNO_3\). Den relativa ordningen av syrestyrkor och ungefärliga värden för \(K_a\) och \(pK_a\) för de starka syrorna högst upp i tabell \(\PageIndex{1}\) bestämdes med hjälp av mätningar som denna och olika icke-vattenhaltiga lösningsmedel.
I vattenlösningar är \(H_3O^+\) den starkaste syran och \(OH^-\) den starkaste basen som kan existera i jämvikt med \(H_2O\).
Den utjämnande effekten gäller även för lösningar av starka baser: I vattenlösning jämnas alla baser som är starkare än OH- ut till OH-styrkan eftersom OH- är den starkaste basen som kan existera i jämvikt med vatten. Salter som \(K_2O\), \(NaOCH_3\) (natriummetoxid) och \(NaNH_2\) (natriumamid eller natriumamid), vars anjoner är konjugerade baser av arter som skulle ligga under vatten i tabell \(\PageIndex{2}\), är alla starka baser som reagerar i stort sett fullständigt (och ofta våldsamt) med vatten genom att ta emot en proton för att ge en lösning av \(OH^-\) och motsvarande katjon:
\
\
\
Andra exempel som du kan stöta på är kaliumhydrid (\(KH\)) och metallorganiska föreningar som metyllitium (\(CH_3Li\)).
Polyprotiska syror och baser
Som du lärt dig innehåller polyprotiska syror som \(H_2SO_4\), \(H_3PO_4\) och \(H_2CO_3\) mer än en joniserbar proton, och protonerna försvinner stegvis. Den fullständigt protonerade arten är alltid den starkaste syran eftersom det är lättare att avlägsna en proton från en neutral molekyl än från en negativt laddad jon. Syrastyrkan minskar alltså med förlusten av efterföljande protoner, och på motsvarande sätt ökar \(pK_a\). Ta till exempel \(H_2SO_4\):
\
Jämvikten i den första reaktionen ligger långt till höger, vilket är förenligt med att \(H_2SO_4\) är en stark syra. I den andra reaktionen är däremot märkbara mängder av både \(HSO_4^-\) och \(SO_4^{2-}\) närvarande vid jämvikt.
För en polyprotisk syra minskar syrastyrkan och \(pK_a\) ökar med den sekventiella förlusten av varje proton.
Vätesulfatjonen (\(HSO_4^-\)) är både den konjugerade basen av \(H_2SO_4\) och den konjugerade syran av \(SO_4^{2-}\). Precis som vatten kan HSO4- därför fungera som antingen en syra eller en bas, beroende på om den andra reaktanten är en starkare syra eller en starkare bas. Omvänt är sulfatjonen (\(SO_4^{2-}\)) en polyprotisk bas som kan ta emot två protoner stegvis:
\
\
Som alla andra konjugerade syra-baspar är styrkorna hos de konjugerade syrorna och baserna relaterade till varandra genom \(pK_a\) + \(pK_b\) = pKw. Tänk till exempel på det konjugerade syra-basparet \(HSO_4^-/ SO_4^{2-}\). Av tabell \(\(\PageIndex{1}\) ser vi att \(pK_a\) för \(HSO_4^-\) är 1,99. Följaktligen är \(pK_b\) för \(SO_4^{2-}\) 14,00 – 1,99 = 12,01. Sulfat är alltså en ganska svag bas, medan \(OH^-\) är en stark bas, så den jämvikt som visas i ekvation \(\ref{16.6}\) ligger till vänster. Jonen \(HSO_4^-\) är också en mycket svag bas (\(pK_a\) för \(H_2SO_4\) = 2,0, \(pK_b\) för \(HSO_4^- = 14 – (-2,0) = 16\)), vilket stämmer överens med vad vi förväntar oss för den konjugerade basen till en stark syra.
Exempel \(\PageIndex{2}\)
Förutsäg om jämvikten för varje reaktion ligger till vänster eller höger som det står skrivet.
- \(NH^+_{4(aq)}+PO^{3-}_{4(aq)} \rightleftharpoons NH_{3(aq)}+HPO^{2−}_{4(aq)}\)
- \(CH_3CH_2CO_2H_{(aq)}+CN^−_{(aq)} \rightleftharpoons CH_3CH_2CO^-_{2(aq)}+HCN_{(aq)}\)
Givet: balanserad kemisk ekvation
Sökt: jämviktsläge
Strategi:
Identifiera de konjugerade syra-basparen i varje reaktion. Hänvisa sedan till tabellerna \(\PageIndex{1}\)och\(\PageIndex{2}\) och figur \(\PageIndex{2}\) för att bestämma vilken som är den starkare syran och basen. Jämvikt gynnar alltid bildandet av det svagare syra-basparet.
Lösning:
De konjugerade syra-basparen är \(NH_4^+/NH_3\) och \(HPO_4^{2-}/PO_4^{3-}\). Enligt tabellerna \(\PageIndex{1}\) och \(\PageIndex{2}\) är \(NH_4^+\) en starkare syra (\(pK_a = 9.25\)) än \(HPO_4^{2-}\) (pKa = 12,32), och \(PO_4^{3-}\) är en starkare bas (\(pK_b = 1,68\)) än \(NH_3\) (\(pK_b = 4,75\)). Jämvikten kommer därför att ligga till höger, vilket gynnar bildandet av det svagare syra-basparet:
\
De konjugerade syra-basparen är \(CH_3CH_2CO_2H/CH_3CH_2CO_2_2^-\) och \(HCN/CN^-\). Enligt tabell \(\PageIndex{1}\) är HCN en svag syra (pKa = 9,21) och \(CN^-\) en måttligt svag bas (pKb = 4,79). Propionsyra (\(CH_3CH_2CO_2H\)) finns dock inte med i tabell \(\PageIndex{1}\). I en situation som denna är den bästa metoden att leta efter en liknande förening vars syra-basegenskaper finns förtecknade. Propionsyra och ättiksyra är till exempel identiska med undantag för de grupper som är knutna till kolatomen i karboxylsyran (\(\ce{-CH_2CH_3}\) jämfört med \(\ce{-CH_3}\)), så vi kan förvänta oss att de två föreningarna har liknande syra-basegenskaper. I synnerhet skulle vi förvänta oss att \(pK_a\) för propionsyra skulle vara av liknande storlek som \(pK_a\) för ättiksyra. (I själva verket är \(pK_a\) för propionsyra 4,87, jämfört med 4,76 för ättiksyra, vilket gör propionsyra till en något svagare syra än ättiksyra). Propionsyra borde alltså vara en betydligt starkare syra än \(HCN\). Eftersom den starkare syran bildar den svagare konjugerade basen förutspår vi att cyanid kommer att vara en starkare bas än propionat. Jämvikten kommer därför att ligga till höger, vilket gynnar bildandet av det svagare syra-basparet:
\
Övningsuppgift \(\PageIndex{1}\)
Förutsäg om jämvikten för varje reaktion ligger till vänster eller till höger som det står skrivet.
- \(H_2O_{(l)}+HS^-_{(aq)}) \rightleftharpoons OH^−_{(aq)}+H_2S_{(aq)}\)
- \(HCO^−_{2(aq)}+HSO^−_{4(aq)} \rightleftharpoons HCO_2H_{(aq)}+SO^{2-}_{4(aq)}\)
Svar a
vänster
Svar b
vänster
Sammanfattning
Syra-basreaktioner innehåller alltid två konjugerade syra-baspar. Varje syra och varje bas har en associerad joniseringskonstant som motsvarar dess syra- eller basstyrka. Två arter som skiljer sig åt med endast en proton utgör ett konjugerat syra-baspar. Storleken på jämviktskonstanten för en joniseringsreaktion kan användas för att bestämma den relativa styrkan hos syror och baser. För en vattenlösning av en svag syra kallas dissociationskonstanten för syrajoniseringskonstanten (\(K_a\)). På samma sätt är jämviktskonstanten för reaktionen av en svag bas med vatten basjoniseringskonstanten (\(K_b\)). För varje konjugerat syra-baspar gäller \(K_aK_b = K_w\). Mindre värden på \(pK_a\) motsvarar större syrajoniseringskonstanter och därmed starkare syror. Omvänt motsvarar mindre värden på \(pK_b\) större joniseringskonstanter för baser och därmed starkare baser. Vid 25 °C är \(pK_a + pK_b = 14,00\). Syra-basreaktioner går alltid i den riktning som ger upphov till det svagare syra-basparet. Ingen syra som är starkare än \(H_3O^+\) och ingen bas som är starkare än \(OH^-\) kan existera i vattenlösning, vilket leder till det fenomen som kallas utjämnande effekt. Polyprotiska syror (och baser) förlorar (och får) protoner stegvis, där den helt protonerade arten är den starkaste syran och den helt deprotonerade arten den starkaste basen.
Nyckelekvationer
- Syrans joniseringskonstant: \=\dfrac{}{}{} \]
- Basjoniseringskonstant: \= \dfrac{}{}{} \]
- Samband mellan \(K_a\) och \(K_b\) för ett konjugerat syra-baspar: \
- Definition av \(pK_a\): \
- Definition av \(pK_b\): \ \
- Samband mellan \(pK_a\) och \(pK_b\) för ett konjugerat syra-baspar: \ \
Kontributorer och tillskrivningar
-
Stephen Lower, Professor Emeritus (Simon Fraser U.) Chem1 Virtual Textbook