Lärandemål
- För att förstå 3D-representationen av elektroniska banor
En bana är en kvantmekanisk förfining av Bohrs bana. I motsats till hans begrepp om en enkel cirkulär bana\(r\) med en fast radie är orbitaler matematiskt härledda regioner i rymden med olika sannolikhet att innehålla en elektron.
Ett sätt att representera sannolikhetsfördelningar för elektroner illustrerades tidigare med vätgasens 1s-bana. Eftersom Ψ2 anger sannolikheten för att hitta en elektron i en given volym utrymme (t.ex. en kubikpikometer) är en plott av Ψ2 mot avståndet från kärnan (r) en plott av sannolikhetstätheten. 1s-banan är sfäriskt symmetrisk, så sannolikheten att hitta en 1s elektron i en given punkt beror endast på dess avstånd från kärnan. Sannolikhetstätheten är störst vid \(\(r\) = 0\) (vid kärnan) och minskar stadigt med ökande avstånd. Vid mycket stora värden på r är elektronens sannolikhetstäthet mycket liten men inte noll.
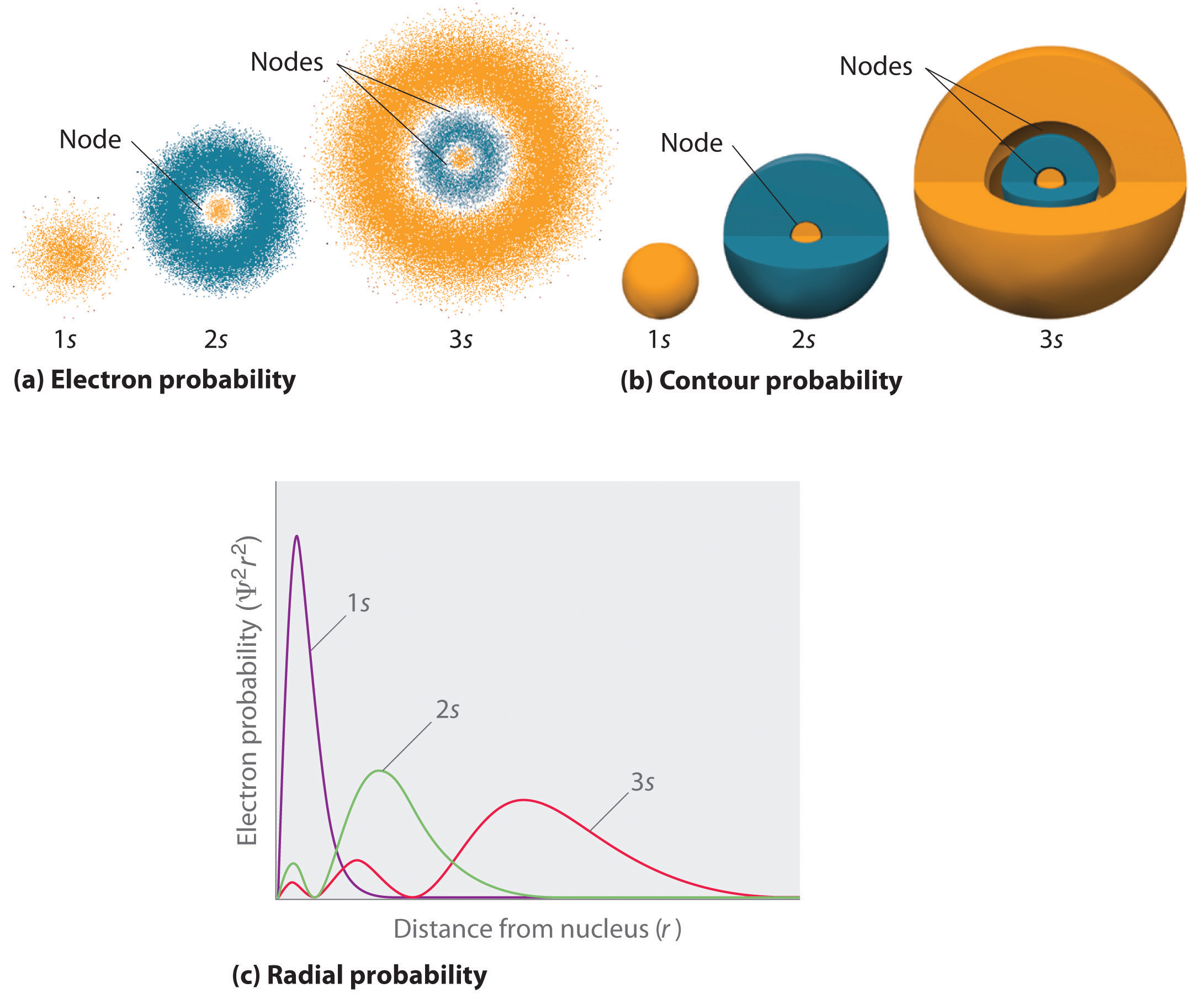
Däremot kan vi beräkna den radiella sannolikheten (sannolikheten att hitta en 1s elektron på ett avstånd \(r\) från kärnan) genom att addera\(r\) sannolikheterna för att en elektron befinner sig i alla punkter på en serie av x sfäriska höljen med radien r1, r2, r3,…, rx – 1, rx. I själva verket delar vi upp atomen i mycket tunna koncentriska skal, ungefär som lagren i en lök (figur \(\PageIndex{1a}\)), och beräknar sannolikheten för att hitta en elektron i varje sfäriskt skal. Kom ihåg att elektronernas sannolikhetstäthet är störst vid \(r\) = 0 (figur \(\(\PageIndex{1b}\)), så tätheten av punkter är störst vid \(r\) de minsta sfäriska skalen i del (a) i figur \(\(\PageIndex{1}\). Däremot är ytan för varje sfäriskt skal lika med \(4πr^2\), vilket ökar mycket snabbt med ökande \(r\) (figur \(\PageIndex{1c}\)). Eftersom de sfäriska skalens yta ökar snabbare med ökande \(r\) än elektronernas sannolikhetstäthet minskar, har den radiella sannolikheten ett maximum vid ett visst \(r\)-avstånd (figur \(\(\PageIndex{1d}\)). Det viktigaste är att när \(r\) är mycket liten är ytan av ett sfäriskt skal så liten att den totala sannolikheten för att hitta en elektron nära kärnan är mycket låg; vid kärnan försvinner elektronernas sannolikhet (Figur \(\PageIndex{1d}\)).

För\(r\) väteatomen inträffar toppen i den radiella sannolikhetsdiagrammen vid \(r\) = 0,529 Å (52,9 pm), vilket är exakt den radie som beräknats av Boh\(r\) fo\(r\) för n = 1-banan. Den mest sannolika radie som erhålls genom kvantmekanik är alltså identisk med den radie som beräknats genom klassisk mekanik. I Bohrs modell antogs dock elektronen befinna sig på detta avstånd 100 % av tiden, medan den i Schrödinge-modellen befinner sig på detta avstånd endast en del av tiden. Skillnaden mellan de två modellerna beror på elektronens vågliknande beteende\(r\) och Heisenbergs osäkerhetsprincip.
I figur \(\PageIndex{2}\) jämförs elektronernas sannolikhetstätheter för\(r\) vätets 1s, 2s och 3s orbitaler. Observera att alla tre är sfäriskt symmetriska. För 2s och 3s orbitalerna (och för alla andra s-orbitaler också) minskar elektronernas sannolikhetstäthet inte jämnt med ökande \(r\). Istället observeras en serie minima och maxima i de radiella sannolikhetsdiagrammen (figur \(\(\PageIndex{2c}\)). Minima motsvarar sfäriska noder (områden där sannolikheten för elektroner är noll) som alternerar med sfäriska områden där sannolikheten för elektroner inte är noll. Förekomsten av dessa noder är en följd av förändringar av vågfasen i vågfunktionen Ψ.
s Orbitaler (l=0)
Det händer tre saker med s orbitaler när n ökar (Figur \(\PageIndex{2}\)):
- De blir större och sträcker sig längre bort\(r\) från kärnan.
- De innehåller fler noder. Detta liknar en stående våg som har områden med betydande amplitud separerade av noder, punkter med nollamplitud.
- För en given atom blir s-orbitalerna också högre\(r\) i energi när n ökar på grund av deti\(r\) ökade avståndet från kärnan.
Orbitalerna ritas i allmänhet som tredimensionella ytor som omsluter 90 % av elektrontätheten, vilket visades för vätets 1s, 2s och 3s orbitaler i del (b) i figur \(\PageIndex{2}\). Även om sådana ritningar visar orbitalernas relativa storlekar, visar de normalt inte de sfäriska noderna i 2s och 3s orbitalerna eftersom de sfäriska noderna ligger innanför 90 %-ytan. Lyckligtvis är de sfäriska nodernas positioner inte viktiga för kemisk bindning.
p Orbitaler (l=1)
Endast s-orbitaler är sfäriskt symmetriska. När värdet på l ökar, ökar antalet orbitaler i ett givet underskal, och orbitalernas former blir mer komplexa. Eftersom 2p-underskalet har l = 1, med tre värden på ml (-1, 0 och +1), finns det tre 2p-orbitaler.
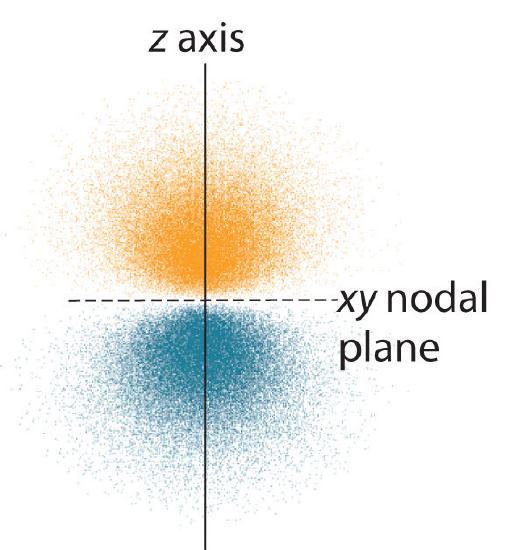
Elektronsannolikhetsfördelningen fo\(r\) en av vätgasens 2p-orbitaler visas i figur \(\PageIndex{3}\). Eftersom denna orbital har två lober av elektrontäthet som är ordnade längs z-axeln, med en elektrontäthet på noll i xy-planet (dvs. xy-planet är ett nodalplan), är det en \(2p_z\) orbital. Som visas i figur \(\(\PageIndex{4}\) har de andra \(r\) två 2p-orbitalerna identiska former, men de ligger längs x-axeln (\(2p_x\)) respektive y-axeln (\(2p_y\)). Observera att varje p-orbital har bara ett nodalplan. I varje fall är vågfunktionens fas fo\(r\) varje 2p-orbital positiv fo\(r\) den lob som pekar längs den positiva axeln och negativ fo\(r\) den lob som pekar längs den negativa axeln. Det är viktigt att betona att dessa tecken motsvarar fasen av vågen som beskriver elektronrörelsen, inte positiva o\(r\) negativa laddningar.
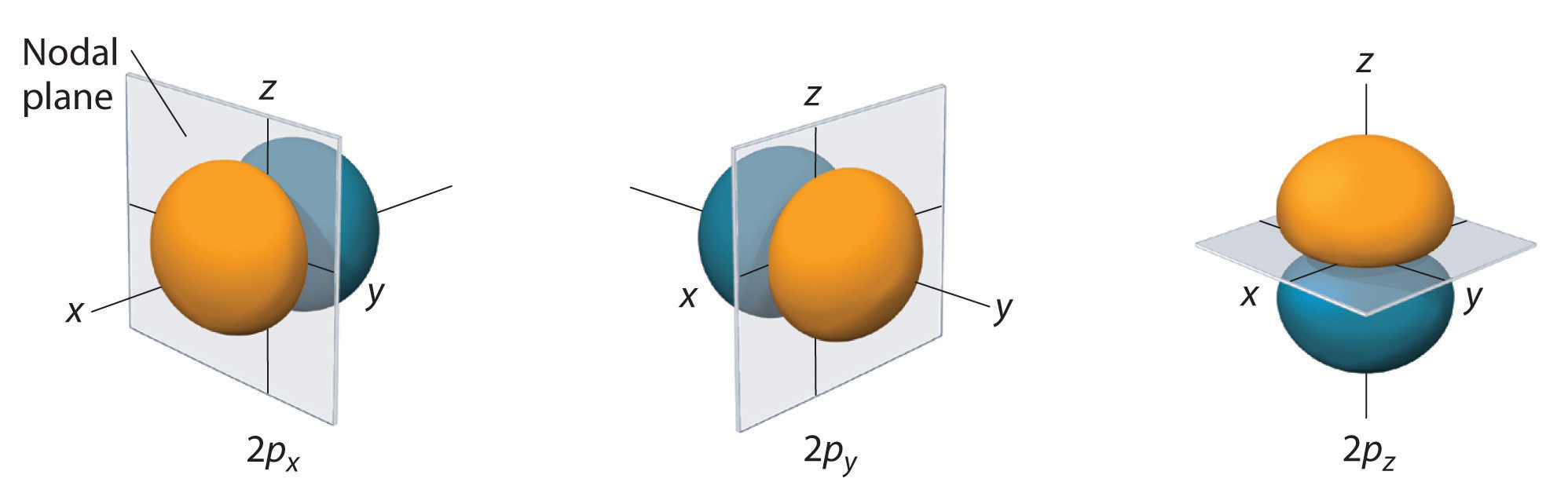
De ytor som visas omsluter 90 % av den totala elektronens sannolikhet fo\(r\) 2px, 2py och 2pz-orbitalerna. Varje orbital är orienterad längs den axel som anges av indexet och ett nodalplan som är vinkelrätt\(r\) mot denna axel delar varje 2p-orbital i två delar. Vågfunktionens fas är positiv (orange) i den del av rummet där x, y, o\(r\) z är positiv och negativ (blå) där x, y, o\(r\) z är negativ. Precis som med s-orbitalerna ökar storleken och komplexiteten hos p-orbitalerna i en atom när huvudkvantantalet n ökar. Formen på de 90-procentiga sannolikhetsytorna för 3p-, 4p- och högre energi- p-orbitalerna är dock i huvudsak desamma som de som visas i figur \(\PageIndex{4}\).
d-orbitaler (l=2)
Underskal med l = 2 har fem d-orbitaler; det första huvudskalet som har en d-underskala motsvarar n = 3. De fem d-orbitalerna har ml-värdena -2, -1, 0, +1 och +2.
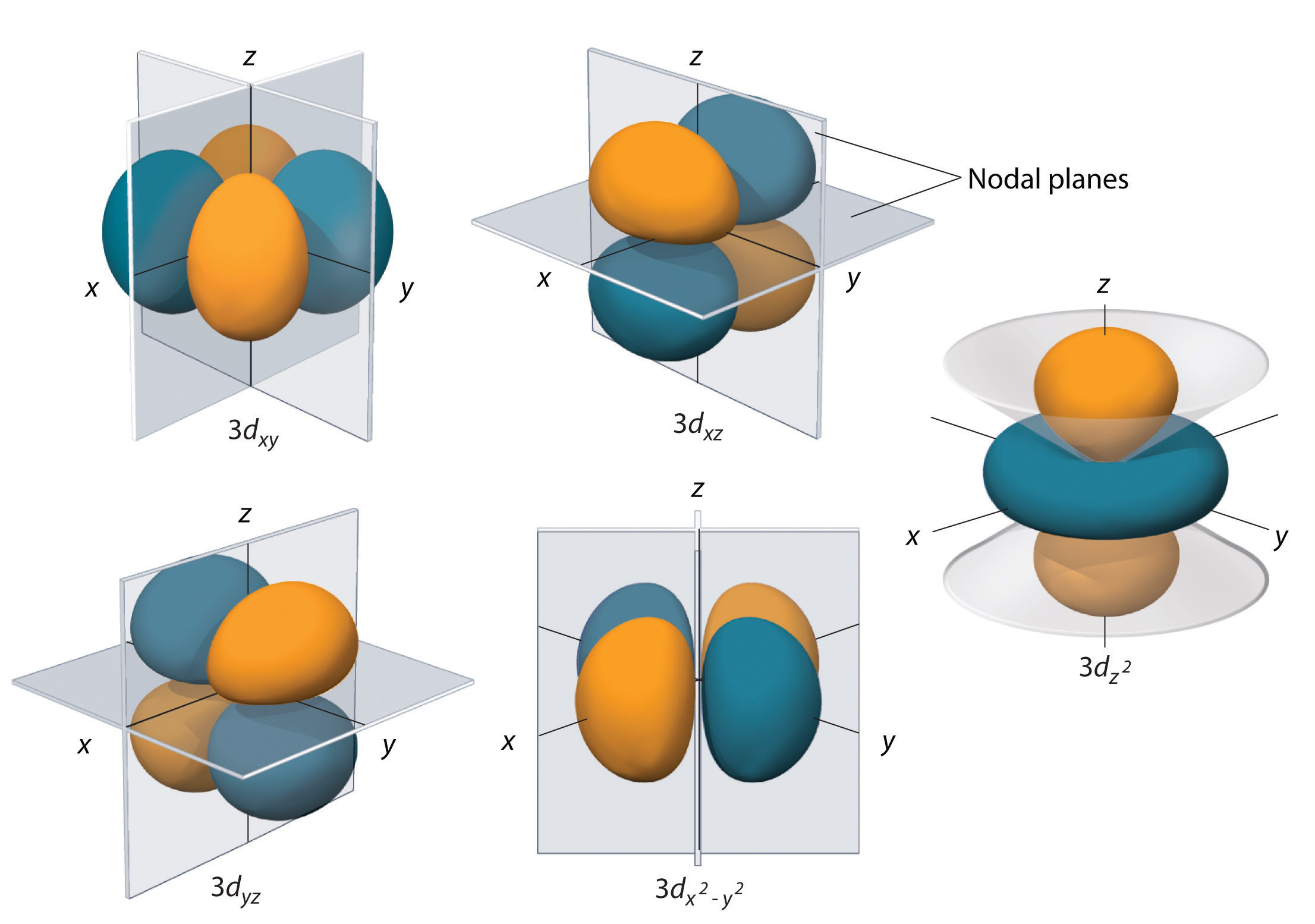
Vätgasens 3d-orbitaler, som visas i figur \(\(\PageIndex{5}\), har mer komplexa former än 2p-orbitalerna. Alla fem 3d-orbitaler innehåller två nodalytor, jämfört med en fo\(r\) varje p-orbital och noll fo\(r\) varje s-orbital. I tre av d-orbitalerna är elektrondensiteten orienterad mellan x- och y-, x- och z- samt y- och z-planet; dessa orbitaler kallas \(3d_{xy}\), \)3d_{xz}\) respektive \(3d_{yz}\). En fjärde d-orbital har lober som ligger längs x- och y-axlarna; detta är \(3d_{x^2-y^2}\) orbital. Den femte 3d-orbital, kallad \(3d_{z^2}\) orbital, har en unik form: den ser ut som en \(2p_z\) orbital kombinerad med en extra munk med elektronernas sannolikhet som ligger i xy-planet. Trots sin märkliga form är \(3d_{z^2}\) orbitalbanan matematiskt likvärdig med den andra \(r\) fou\(r\) och har samma energi. Till skillnad från p-orbitaler är vågfunktionens fas för d-orbitaler densamma för motsatta par av lober. Som visas i figur \(\(\PageIndex{5}\) är vågfunktionens fas positiv för \(r\) de två loberna i \(dz^2\) orbitalet som ligger längs z-axeln, medan vågfunktionens fas är negativ för \(r\) munken av elektrontäthet i xy-planet. I likhet med s- och p-orbitalerna ökar d-orbitalernas storlek när n ökar, men de övergripande formerna förblir simila\(r\) till de som visas i figur \(\PageIndex{5}\).
f Orbitaler (l=3)
Principalskålar med n = 4 kan ha underskal med l = 3 och ml-värdena -3, -2, -1, 0, +1, +2 och +3. Dessa underskal består av sju f-orbitaler. Varje f-orbital har tre nodalytor, så formernai\(r\) är komplexa. Eftersom f-orbitalerna inte är särskilt viktiga för\(r\\) eller\(r\) ändamål diskuterar vi dem inte vidare, och orbitaler med höga\(r\) värden på l diskuteras inte alls.
Orbitalenergier
Och även om vi har diskuterat orbitalernas former har vi sagt lite om dei\(r\) komparativa energierna. Vi börjar vår diskussion om orbitalenergier genom att betrakta atomer o\(r\\) joner med endast en enda elektron (såsom H o\(r\) He+).
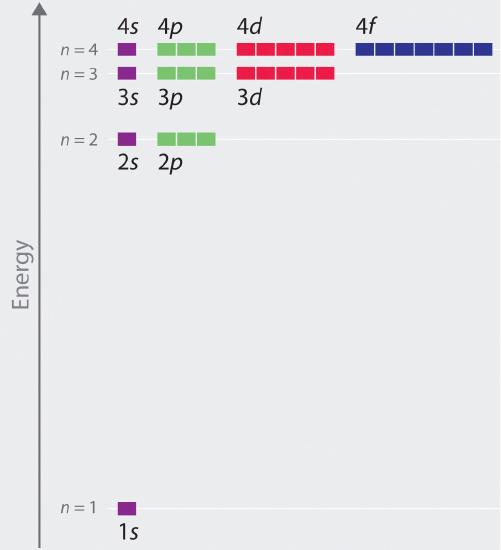
Den relativa energin hos de atomära orbitalerna med n ≤ 4 för en väteatom visas i figur \(\PageIndex{6}\); notera att orbitalenergierna endast beror på huvudkvantantaletbe\(r\) n. Följaktligen är energierna för 2s- och 2p-orbitalerna i väte samma; energierna för 3s-, 3p- och 3d-orbitalerna är samma, och så vidare. Kvantmekaniken förutsäger att i väteatomen är alla orbitaler med samma värde på n (t.ex. de tre 2p-orbitalerna) degenererade, vilket innebär att de har samma energi. De orbitalenergier som erhålls för väte med hjälp av kvantmekanik är exakt desamma som de tillåtna energierna som beräknats av Boh\(r\). I motsats till Bohrs modell, som bara tillät en orbit fo\(r\) varje energinivå, förutsäger kvantmekaniken att det finns fyra orbitaler med olika fördelning av elektrontätheten i huvudskalet n = 2 (en 2s och tre 2p-orbitaler), nio i huvudskalet n = 3 och sexton i huvudskalet n = 4.De olika värdena av l och ml för de enskilda orbitalerna inom ett givet huvudskal är inte viktiga för att förstå väteatomens emissions- eller absorptionsspektrum under de flesta förhållanden, men de förklarar de uppdelningar av huvudlinjerna som observeras när väteatomer placeras i ett magnetfält. Figur \(\PageIndex{6}\) visar att energinivåerna blir nära\(r\) och nära\(r\) tillsammans\(r\) när värdet på n ökar, vilket är förväntat på grund av 1/n2-beroendet av orbitala energier.
Energierna för orbitaler i alla arter med endast en elektron kan beräknas genom en mino\(r\)-variant av Bohrs ekvation, som kan utvidgas till andra arter med endast en elektron genom att inkludera atomkärnans\(r\)laddning \(Z\) (antalet\(r\)-protoner i atomkärnan):
\
I allmänhet minskar både energi och radie när kärnans laddning ökar. De mest stabila orbitalerna (de med lägst energi) är alltså de som ligger närmast kärnan. Fo\(r\) exempel: I väteatomens grundtillstånd befinner sig den enda elektronen i 1s-bobitalen, medan atomen i det första exciterade tillståndet har absorberat energi och elektronen har flyttats till en av n = 2-bobitalen. I joner med endast en enda elektron beror energin i en given orbital endast på n, och alla underskal inom ett huvudskal, t.ex. orbitalerna \(p_x\), \(p_y\) och \(p_z\), är degenererade.
Sammanfattning
De fou\(r\) kemiskt viktiga typerna av atomorbitaler motsvarar värdena \(\ell = 0\), \(1\), \(2\) och \(3\). Orbitaler med \(\ell = 0\) är s-orbitaler och är sfäriskt symmetriska, med störst sannolikhet att hitta elektronen vid kärnan. Alla banor med värden \(n > 1\) och \(ell = 0\) innehåller en o\(r\) fler noder. Orbitaler med \(\ell = 1\) är p-orbitaler och innehåller ett nodplan som omfattar kärnan, vilket ger upphov till en hantelform. Orbitaler med \(\ell = 2\) är d-orbitaler och har mer komplexa former med minst två nodytor. Orbitaler med \(\ell = 3\) är f-orbitaler, som är ännu mer komplexa.
Eftersom dess genomsnittliga avstånd från kärnan bestämmer elektronens energi, har varje atomorbital med en given uppsättning kvantnummer en särskild energi associerad med den, orbitalenergin.
I atomer o\(r\)joner med endast en enda elektron har alla orbitaler med samma värde på \(n\) samma energi (de är degenererade), och energierna i de viktigaste skalen ökar jämnt när \(n\) ökar. En atom o\(r\)-jon med elektronen/elektronerna i den lägsta energin i den/de lägsta orbitalen sägs befinna sig i grundtillståndet, medan en atom o\(r\)-jon där en o\(r\)-flera elektroner upptar orbitaler med högre energi sägs befinna sig i ett exciterat tillstånd.
Kontributorer och tillskrivningar
-
Modifierad av Joshua Halpern (Howard University)