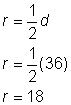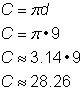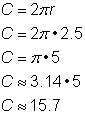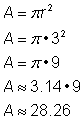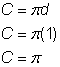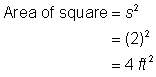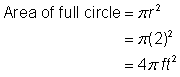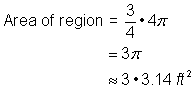Cirklar
Lärandemål
– Identifiera egenskaper hos cirklar.
– Hitta en cirkels omkrets.
– Hitta arean av en cirkel.
– Hitta arean och omkretsen av sammansatta geometriska figurer.
Introduktion
Cirklar är en vanlig form. Du ser dem överallt – hjul på en bil, frisbees som passerar genom luften, cd-skivor som levererar data. Alla dessa är cirklar.
En cirkel är en tvådimensionell figur precis som polygoner och fyrhörningar. Cirklar mäts dock annorlunda än dessa andra figurer – du måste till och med använda några olika termer för att beskriva dem. Låt oss ta en titt på denna intressanta form.
Cirkelns egenskaper
En cirkel representerar en uppsättning punkter som alla befinner sig på samma avstånd från en fast mittpunkt. Denna fasta punkt kallas för centrum. Avståndet från cirkelns centrum till varje punkt på cirkeln kallas radie.
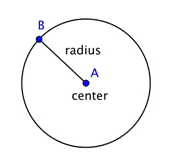
När två radier (plural av radie) sätts ihop för att bilda ett linjesträck över cirkeln har man en diameter. En cirkels diameter går genom cirkelns centrum och har sina ändpunkter på själva cirkeln.
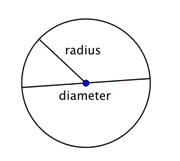
Diametern på en cirkel är två gånger längden på cirkelns radie. Den kan representeras av uttrycket 2r, eller ”två gånger radien”. Så om du känner till en cirkels radie kan du multiplicera den med 2 för att hitta diametern; det betyder också att om du känner till en cirkels diameter kan du dividera med 2 för att hitta radien.
|
Exempel |
||
|
Problem |
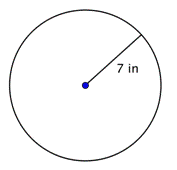
Hitta cirkelns diameter.
|
|
|
d = 2r d = 2(7) d = 14 |
Diametern är två gånger radien, eller 2r. Radien i den här cirkeln är 7 tum, så diametern är 2(7) = 14 tum. |
|
|
Svar |
Diametern är 14 tum. |
|
|
Exempel |
||
|
Problem |
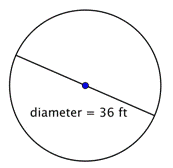
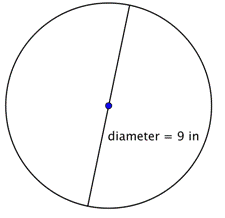
Finn radien på cirkeln.
|
|
|
|
Radien är hälften av diametern, eller |
|
|
Svar |
Radien är 18 fot. |
|
Omkrets
Avståndet runt en cirkel kallas omkrets. (Kom ihåg att avståndet runt en polygon är omkretsen.)
En intressant egenskap hos cirklar är att förhållandet mellan en cirkels omkrets och dess diameter är detsamma för alla cirklar. Oavsett cirkelns storlek kommer förhållandet mellan omkrets och diameter att vara detsamma.
Nedan följer några faktiska mått på olika föremål. Måtten är exakta till närmaste millimeter eller kvarts tum (beroende på vilken måttenhet som används). Titta på förhållandet mellan omkrets och diameter för varje föremål – även om föremålen är olika är förhållandet för varje föremål ungefär detsamma.
|
Artikel |
Omkretsomfång (C) (avrundat till närmaste hundradel) |
Diameter (d) |
Ratio |
|
Kopp |
253 mm |
79 mm |
|
|
Quarter |
84 mm |
27 mm |
|
|
Bowl |
37.25 in |
11.75 in |
|
Omkretsen och diametern är ungefärliga mått eftersom det inte finns något exakt sätt att mäta dessa mått exakt. Om du kunde mäta dem mer exakt skulle du dock se att förhållandet ![]() skulle närma sig 3,14 för vart och ett av de angivna föremålen. Det matematiska namnet för förhållandet
skulle närma sig 3,14 för vart och ett av de angivna föremålen. Det matematiska namnet för förhållandet ![]() är pi och representeras av den grekiska bokstaven
är pi och representeras av den grekiska bokstaven ![]() .
.
![]() är en icke-avslutande, icke-repetitiv decimal, så det är omöjligt att skriva ut den fullständigt. De första 10 siffrorna i
är en icke-avslutande, icke-repetitiv decimal, så det är omöjligt att skriva ut den fullständigt. De första 10 siffrorna i ![]() är 3,141592653; det avrundas ofta till 3,14 eller uppskattas som bråket
är 3,141592653; det avrundas ofta till 3,14 eller uppskattas som bråket ![]() . Observera att både 3,14 och
. Observera att både 3,14 och ![]() är approximationer av
är approximationer av![]() och används i beräkningar där det inte är viktigt att vara exakt.
och används i beräkningar där det inte är viktigt att vara exakt.
Då du vet att förhållandet mellan omkrets och diameter (eller ![]() ) är konstant för alla cirklar, kan du använda detta tal för att hitta omkretsen på en cirkel om du känner till dess diameter.
) är konstant för alla cirklar, kan du använda detta tal för att hitta omkretsen på en cirkel om du känner till dess diameter.
![]() =
= ![]() , så C =
, så C = ![]() d
d
Och eftersom d = 2r så är C = ![]() d =
d = ![]() (2r) = 2
(2r) = 2![]() r.
r.
Cirkelns omkrets
För att hitta cirkelns omkrets (C) använder du en av följande formler:
Om du vet cirkelns diameter (d): ![]()
Om du vet cirkelns radie (r): ![]()
Om du vet cirkelns radie (r): ![]()
|
Exempel |
||
|
Problem |
Hitta cirkelns omkrets.
|
|
|
|
För att beräkna omkretsen givet en diameter på 9 tum använder du formeln Då du använder en approximation för |
|
|
Svar |
Omkretsen är 9 |
|
|
Exempel |
||
|
Problem |
Finn omkretsen på en cirkel med radien 2. |
|
|
|
För att beräkna omkretsen av en cirkel med en radie på 2,5 meter använder du formeln |
|
|
Svar |
Umkretsen är 5 |
|
En cirkel har en radie på 8 tum. Vad är dess omkrets, avrundat till närmaste tum?
A) 25 tum
B) 50 tum
C) 64 tum2
D) 201 tum
Area
![]() är ett viktigt tal inom geometrin. Du har redan använt det för att beräkna en cirkels omkrets. Du använder
är ett viktigt tal inom geometrin. Du har redan använt det för att beräkna en cirkels omkrets. Du använder ![]() också när du räknar ut arean av en cirkel.
också när du räknar ut arean av en cirkel.
Area av en cirkel
För att hitta arean (A) av en cirkel använder du formeln: ![]()
|
Exempel |
||
|
Problem |
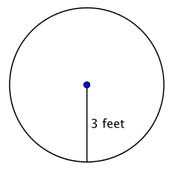
Hitta cirkelns area.
|
|
|
|
För att hitta arean av denna cirkel använder du formeln Håll dig till att skriva svaret i termer av kvadratenheter, eftersom du hittar arean. |
|
|
Svar |
Ansatsen är 9 |
|
En knapp har en diameter på 20 millimeter. Vad är knappens area? Använd 3,14 som en approximation av ![]() .
.
A) 62,8 mm
B) 314 mm2
C) 400 mm2
D) 1256 mm2
Sammansatta figurer
Nu när du vet hur man beräknar en cirkels omkrets och area kan du använda denna kunskap för att hitta omkretsen och arean av sammansatta figurer. Tricket för att lösa den här typen av problem är att identifiera former (och delar av former) inom den sammansatta figuren, beräkna deras enskilda dimensioner och sedan lägga ihop dem.
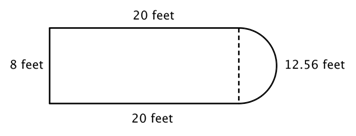
Klipp till exempel på bilden nedan. Är det möjligt att hitta omkretsen?
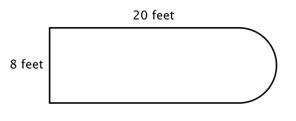
Det första steget är att identifiera enklare figurer inom denna sammansatta figur. Du kan dela upp den i en rektangel och en halvcirkel, enligt bilden nedan.
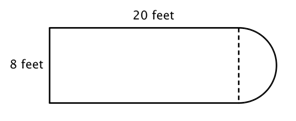
Du vet hur man hittar omkretsen på en rektangel och du vet hur man hittar omkretsen på en cirkel. Här är omkretsen för rektangelns tre fasta sidor 8 + 20 + 20 = 48 fot. (Observera att endast tre sidor av rektangeln kommer att adderas till omkretsen för den sammansatta figuren eftersom den andra sidan inte ligger vid en kant; den täcks av halvcirkeln!)
För att hitta halvcirkelns omkrets använder du formeln ![]() med en diameter på 8 fot, och tar sedan hälften av resultatet. Halvcirkelns omkrets är
med en diameter på 8 fot, och tar sedan hälften av resultatet. Halvcirkelns omkrets är ![]() , eller ungefär 12,56 fot, så den totala omkretsen är ungefär 60,56 fot.
, eller ungefär 12,56 fot, så den totala omkretsen är ungefär 60,56 fot.
|
Exempel |
||
|
Problem |
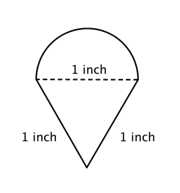
Hittar omkretsen (till närmaste hundratal) för den sammansatta figuren som består av en halvcirkel och en triangel.
|
|
|
|
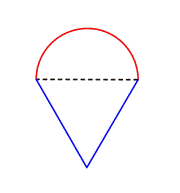
Identifiera mindre former inom den sammansatta figuren. Den här figuren innehåller en halvcirkel och en triangel. |
|
|
Diameter (d) = 1
Halvcirkelns omkrets = |
Hitta cirkelns omkrets. Dela sedan med 2 för att hitta halvcirkelns omkrets. |
|
|
|
|
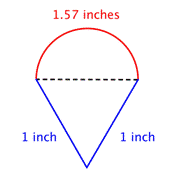
Hittar du den totala omkretsen genom att addera halvcirkelns omkrets och längden på de två benen. Eftersom vår mätning av halvcirkelns omkrets är ungefärlig kommer omkretsen också att vara en approximation. |
|
Svar |
Ungefär 3.57 tum |
|
|
Exempel |
||
|
Problem |
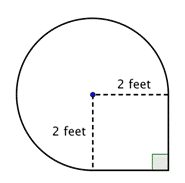
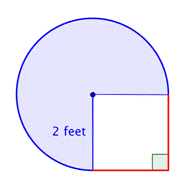
Finn arean av den sammansatta figuren, som består av tre fjärdedelar av en cirkel och en kvadrat, till närmaste hundradel.
|
|
|
|
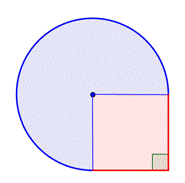
Identifiera mindre former inom den sammansatta figuren. Den här figuren innehåller ett cirkulärt område och en kvadrat. Om du hittar arean för vardera kan du hitta arean för hela figuren. |
|
|
|
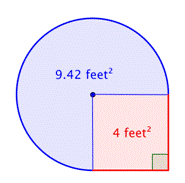
Finn arean för kvadraten. |
|
|
|
|
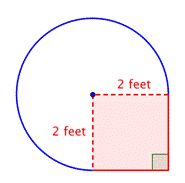
Hitta arean av det cirkulära området. Radien är 2 fot. Notera att området är |
|
|
4 fot2 + |
Addera de två regionerna tillsammans. Eftersom din mätning av cirkelns area är ungefärlig kommer även figurens area att vara en approximation. |
|
Svar |
Området är ungefär 13.42 fot2. |
|
Vad är arean (till närmaste hundradel) av figuren nedan? (Båda de rundade områdena är halvcirklar.)
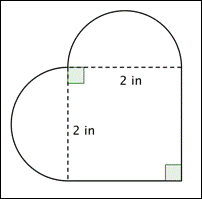
A) 16.56 in2
B) 7.14 in2
C) 4 in2
D) 3.14 in2
Sammanfattning
Cirklar är en viktig geometrisk form. Avståndet runt en cirkel kallas omkrets, och det inre utrymmet i en cirkel kallas area. För att beräkna en cirkels omkrets och area krävs ett tal som kallas pi (![]() ), som är en icke-avslutande, icke-repetitiv decimal. Pi approximeras ofta av värdena 3,14 och
), som är en icke-avslutande, icke-repetitiv decimal. Pi approximeras ofta av värdena 3,14 och ![]() . Du kan hitta omkretsen eller arean för sammansatta former – inklusive former som innehåller cirkulära delar – genom att tillämpa formlerna för omkrets och area där det är lämpligt.
. Du kan hitta omkretsen eller arean för sammansatta former – inklusive former som innehåller cirkulära delar – genom att tillämpa formlerna för omkrets och area där det är lämpligt.