Det som följer är min syn på några matematiska problem med förmodad ”common core-matematik” eller ”ny matematik” som har cirkulerat på internet. Jag anser att de visar oss ett felaktigt genomförande av CCS.

Håll i minnet att inte allt du ser i matematikböcker eller på internet är korrekt utfört utifrån CCS. I vissa av de exempel du ser ser det ut som om folk kastar bort sunt förnuft när de gör matematiska problem för att uppfylla Common Core-standarderna!

Jag är inte förvånad över att implementeringen har slutat ”klantigt” på vissa ställen. CCS är en sådan förändring för de flesta lärare att de behöver mycket stöd och omskolning innan de måste undervisa enligt dem.

Jag har alltid trott att det största problemet med matematikundervisningen i grundskolan i de offentliga skolorna är att många grundskollärare inte förstår matematik tillräckligt bra för att kunna undervisa den på rätt sätt även på grundskolenivå. Många av dem förstår till exempel inte begreppen, varför och varför de algoritmer de undervisar. Det är inte deras fel – problemet går tillbaka till vad de fick lära sig under lärarutbildningen och i sin egen skolgång.

Även själva normdokumentet är något svårt att följa på vissa ställen. Att läsa det kräver en del eftertanke. Jag önskar att någon skulle producera en broschyr som förklarar standarderna på ett enkelt språk och med många exempel.

Dåliga exempel på ”common core” eller ”ny matematik”

Exempel 1

För en kort tid sedan såg jag en bild av subtraktionsstrategier på Facebook som hävdade att den kom från en mattebok för första klass och att den var ”common core-matematik”.”

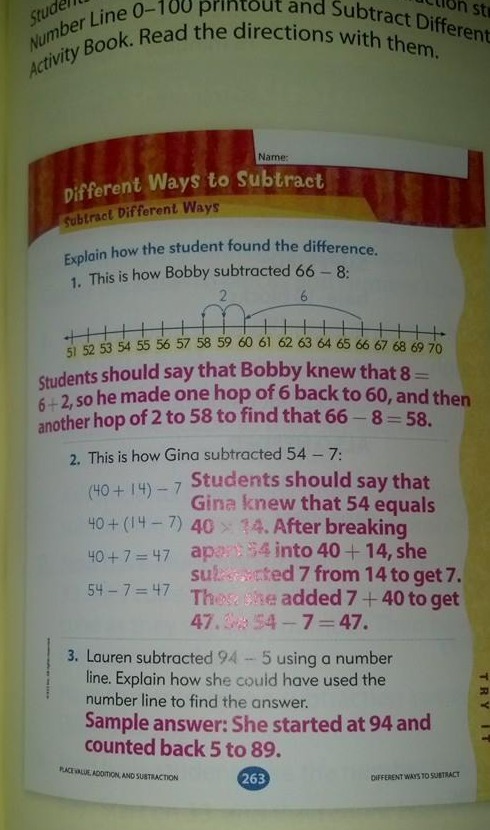
Jag tycker att metod 2 är alldeles för svår för första klass, och jag skulle till och med lämna metod 1 till andra klass.

Den boken verkar dock inte ens överensstämma med Common Core-standarderna. Standarderna för första klass omfattar helt enkelt inte den typen av subtraktionsproblem!

Det här är vad vi hittar i standarderna:

Lägg till och subtrahera inom 20.
1.OA.5
Relatera räkning till addition och subtraktion (t.ex. genom att räkna på 2 för att addera 2).
1.OA.6.
Addera och subtrahera inom 20, och visa att man kan addera och subtrahera inom 10. Använda strategier som att räkna vidare, bilda tio (t.ex. 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14), sönderdela ett tal som leder till tio (t.ex. 13 – 4 = 13 – 3 – 1 = 10 – 1 = 9), använda förhållandet mellan addition och subtraktion (t.ex. vet man att 8 + 4 = 12, så vet man att 12 – 8 = 4), och skapa likvärdiga men enklare eller kända summor (t.ex, addera 6 + 7 genom att skapa den kända ekvivalenten 6 + 6 + 1 = 12 + 1 = 13).

Läroboksexemplet verkar vilja ta upp 1.OA.6 ovan, men det gäller tydligt addition och subtraktion inom 20, inte med större tal.

Senare i standarderna för 1:a klass ser vi två standarder som har att göra med subtraktion av tvåsiffriga tal (inom 100):

1.NBT.5.
Genom ett tvåsiffrigt tal ska du mentalt hitta 10 fler eller 10 färre än talet, utan att behöva räkna; förklara hur du resonerar.
1.NBT.6.
Subtrahera multiplar av 10 i intervallet 10-90 från multiplar av 10 i intervallet 10-90 (positiva eller nollskillnader), med hjälp av konkreta modeller eller ritningar och strategier baserade på platsvärde, operationsegenskaper och/eller förhållandet mellan addition och subtraktion; relatera strategin till en skriven metod och förklara det använda resonemanget.
Marias anmärkning: Detta innebär subtraktioner såsom 34 – 20 eller 89 – 60.

men ingen av dessa inkluderar subtraktioner som 54 – 7 eller 82 – 6. Dessa finns i andra klass:

2.NBT.5
Additera och subtrahera flytande inom 100 med hjälp av strategier baserade på platsvärde, operationsegenskaper och/eller förhållandet mellan addition och subtraktion.

Notera att standarden för årskurs 2 inte anger HUR du subtraherar (om du använder strategier för mentalt räknande eller skriver siffror under varandra och lånar/återgrupperar).

Exempel 2

Från Houghton Mifflin, förmodas:

Juanita vill ge påsar med klistermärken till sina vänner. Hon vill ge lika många klistermärken till varje vän. Hon är inte säker på om hon behöver 4 påsar eller 6 påsar med klistermärken. Hur många klistermärken kan hon köpa så att det inte blir några klistermärken över?

Klistermärkesproblemet har att göra med begreppet minsta gemensamma multipel (LCM). (Svaret är att hon bör köpa 12, 24, 36 eller någon annan multipel av 12 klistermärken, eftersom hon då kan dela upp dem antingen i 4 påsar eller 6 påsar.)

Säkerligen är problemet MYCKET otydligt och dåligt formulerat. Min gissning är att häftet som detta förekommer i helt enkelt är oredigerat. Det är inte själva standardernas fel. Jag håller med Bart Goddard på Math Forum. Detta är ett symptom på den blinda brådskan att ta fram ”verklighetstrogna” historieproblem som i slutändan blir ointressanta.

Utifrån PDF-dokumentet som det förekommer i drar jag slutsatsen att problemet är för fjärde klass, eftersom alla andra ordproblem i häftet motsvarar standarderna för fjärde klass (faktorer, primtal). Men CCS inkluderar inte ens den minsta gemensamma multipeln i standarderna för fjärde klass (den finns i sjätte klass)!!! Något gick verkligen snett med det ordproblemet.

Exempel 3

Även detta är förmodligen från Houghton Mifflin för första klass. Detta stämmer överens med den standard som jag redan citerat ovan:

Addera och subtrahera inom 20.
1.OA.6.
Addera och subtrahera inom 20, och visa att man behärskar addition och subtraktion inom 10. Använda strategier som att räkna vidare, bilda tio (t.ex. 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14), sönderdela ett tal som leder till tio (t.ex. 13 – 4 = 13 – 3 – 1 = 10 – 1 = 9), använda förhållandet mellan addition och subtraktion (t.ex, om man vet att 8 + 4 = 12 vet man att 12 – 8 = 4), och skapa likvärdiga men enklare eller kända summor (t.ex. addera 6 + 7 genom att skapa den kända motsvarigheten 6 + 6 + 1 = 12 + 1 = 13).

För det första har strategin att ”göra tio” att göra med TILLÄGGNING, inte med subtraktion. Vid subtraktion kallas det att ”sönderdela ett tal som leder till en tia”. Så instruktionerna borde lyda: ”Vilket visar ett sätt att sönderdela ett tal som leder till en tia?”. Jag anser att det är fullständigt nonsens att kräva att elever i första klass ska känna till sådan terminologi.

Men det finns ett annat problem här. Om du faktiskt läser alla standarder kommer du att märka att man på flera andra ställen ber eleverna att förklara det resonemang som använts eller att relatera en viss visuell metod till strategin, men INTE i denna standard!

Så som jag ser den här standarden är det meningen att lärarna ska LÄRA ut de olika strategier som nämns och sedan ge eleverna ENKELA additions- och subtraktionsproblem inom 20, till exempel 15 – 8 och 10 – 6. Jag ser INTE att denna standard kräver att eleverna ska känna igen om en viss visuell modell matchar en viss strategi.

Även här ser det ut som om författaren kastar ut sunt förnuft… och faktiskt inte förstår standarderna.

Exempel 4

Exemplet nedan är mycket dåligt formulerat, men KONCEPTet bakom det är mycket bra och finns också i Math Mammoth. Jag kan därför räkna ut vad de vill.

Du ser fem kvadrater. Färga några blå och resten röda. Det är klart.

Färg sedan rutorna i ”talbindningen” på samma sätt. Nummerbindningen går till dessa tre cirklar. Ett barn som har varit med på en lektion där läraren lär ut talbindningar vet förhoppningsvis vad det betyder. Det är samma koncept som en faktafamilj… det översta talet är summan eller totalen (5), och siffrorna som går till de nedre cirklarna motsvarar hur många du färgat blått och hur många rött, i det här fallet 1 och 4.

Då tror jag att de dolda partnerna också är 1 och 4. Visa 1 och 4 fingrarna för en vuxen. Färg slutligen 1 och 4 fingrar på bilden (och inte dina egna fingrar som det låter som).

I min mening är delen om fingrar superflous och förvirrande. Begreppet talbindningar är dock mycket äldre än CCS. Nummerbindningar nämns faktiskt inte i CCS, även om de är kopplade till denna standard:

1.OA.4
Förstå subtraktion som ett problem med okända adderande. Subtrahera till exempel 10 – 8 genom att hitta det tal som ger 10 när det adderas till 8.

och med den här

1.OA.6.
Addera och subtrahera inom 20, genom att visa att man behärskar addition och subtraktion inom 10.

Jag vet inte varför det där arbetsbladet med talbindningar anges som ett exempel på Common Core Math. Det skulle vara mycket bättre att titulera det som ett exempel på ett dåligt formulerat matematiskt arbetsblad som till och med KAN dateras till tiden före Common Core (och som bara återanvänds i just den här läroplanen)… för som jag sa, talbindningar nämns INTE i CCS.

Vad Common Core Math Standards inte är

1. De är inte ”ny matematik”. Jämfört med många matematiska läroplaner som användes på 2000-talet och som betonade icke-traditionella algoritmer, är CCS en tydlig rörelse mot traditionella algoritmer och memorering. Kolla in dessa specifika standarder:
   

   2.OA.2
   Att lägga till och subtrahera inom 20 med hjälp av mentala strategier. I slutet av årskurs 2 kan du alla summor av två ensiffriga tal ur minnet.
   Marias anmärkning: Detta är grundläggande additionsfakta, till exempel 7 + 7 eller 5 + 4.

   3.OA.7
   Men du kan multiplicera och dividera inom 100 med hjälp av strategier som förhållandet mellan multiplikation och division (t.ex. att veta att 8 × 5 = 40 innebär att man vet att 40 ÷ 5 = 8) eller egenskaper hos operationer. I slutet av årskurs 3 kan man ur minnet alla produkter av två ensiffriga tal.
   Marias anmärkning: Detta innebär multiplikationstabeller och grundläggande divisionsfakta.

   4.NBT.4
   Anslutningsvis addera och subtrahera hela tal med flera siffror med hjälp av standardalgoritmen.

   5.NBT.5
   Flyktigt multiplicera hela tal med flera siffror med hjälp av standardalgoritmen.
   Marias anmärkning: Detta innebär inte att eleverna multiplicerar hela tal med flera siffror endast i årskurs 5; detta studeras även i årskurs 3 och 4.

2. Normerna ålägger inte lärare och elever konstiga strategier eller visuella modeller. Många standarder lämnar det upp till lärarna och eleverna. Till exempel:
   

   2.NBT.5
   Att addera och subtrahera inom 100 på ett smidigt sätt med hjälp av strategier som bygger på platsvärde, operationsegenskaper och/eller förhållandet mellan addition och subtraktion.

   Lägg märke till ”och/eller” i meningen ovan. Detta innebär att lärarna och eleverna INTE är begränsade till att använda några specifika strategier eller uppmanas att använda flera strategier. Den traditionella algoritmen att ”låna” är en strategi som bygger på platsvärde, så den finns med här i 2.NBT.5.

   2.NBT.9
   Förklara varför strategier för addition och subtraktion fungerar med hjälp av platsvärde och operationernas egenskaper. Förklaringarna kan stödjas av ritningar eller föremål.

   Det står ”kan stödjas av ritningar” men det tvingar dig inte att göra det, och begränsar dig inte heller till att använda en specifik visuell modell eller typ av ritning.

   3.OA.3
   Använda multiplikation och division inom 100 för att lösa ordproblem insituationer som involverar lika stora grupper, matriser och mätmängder,t.ex. genom att använda ritningar och ekvationer med en symbol för det okända talet för att representera problemet.

   Den studerande MÅSTE inte använda en ritning. Det nämns bara som en möjlighet.

   4.NBT.5
   Multiplicera ett helt tal med upp till fyra siffror med ett ensiffrigt heltal och multiplicera två tvåsiffriga tal, med hjälp av strategier som bygger på platsvärde och operationernas egenskaper. Illustrera och förklara beräkningen med hjälp av ekvationer, rektangulära matriser och/eller areamodeller.

   Lägg märke till ”och/eller”. Illustrera beräkningen men det räcker att illustrera den med hjälp av ekvationer. Du MÅSTE inte illustrera den med hjälp av matriser.

   Detta sagt, vissa standarder nämner en specifik visuell modell, t.ex. en tallinje eller en rektangulär areamodell, men det är mindre vanligt än att ge ett val som i standarderna ovan.

Begreppslig matematik

Det finns en del standarder som berör matematikens begreppsliga sida som grundskollärare kanske inte förstår om de inte får lära sig vad de betyder; till exempel:

5. NF.7b
Tolka division av ett helt tal med ett enhetsbråk och beräkna sådana kvoter. Till exempel skapa en berättelsekontext för 4 ÷ (1/5) och använda en visuell bråkmodell för att visa kvoten. Använd förhållandet mellan multiplikation och division för att förklara att 4 ÷ (1/5) = 20 eftersom 20 × (1/5) = 4.

Ett sådant berättelseproblem skulle kunna vara: Hur många bitar som är 1/5-fot långa kan du skära ut ur en 4-fot lång materialbit? En visuell modell skulle kunna visa 4 helheter, uppdelade i femtedelar. Vi kan då räkna att 4 helheter har totalt 20 femtedelar.

5.NF.4b
Hitta arean av en rektangel med bråkdelars sidlängder genom att kakla den med enhetsrutor med lämpliga enhetsbråkdelars sidlängder, och visa att arean är densamma som den som skulle hittas genom att multiplicera sidlängderna. Multiplicera bråkdelars sidlängder för att hitta arean av rektanglar och representera bråkdelsprodukter som rektangulära areor.

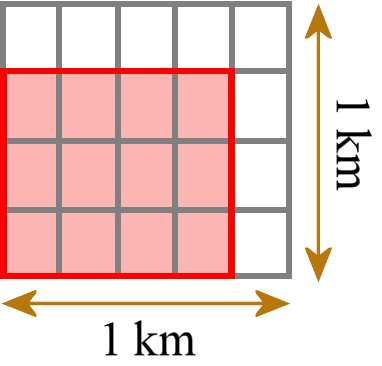Detta innebär till exempel en rektangel med sidlängderna 3/4 km och 4/5 km. Sedan kaklar vi den med små enhetsrektanglar (inte enhetsrutor; här har standarden själv fel terminologi) som var och en har sidlängderna 1/4 km och 1/5 km.

Vi kan räkna hur många små kakelplattor vi behöver. Vi behöver 12 sådana plattor. Varje bricka har en yta på 1/20 km2, så den totala ytan är 12/20 km2. Sedan kontrollerar vi och jämför att vi får samma svar som om vi hade multiplicerat de två sidlängderna med vanlig bråkmultiplikation (3/4 km × 4/5 km = 12/20 km2).

Jag har alltid haft den här typen av problem i mina böcker – till och med innan CCS kom.

En del människor hävdar att barn inte behöver en sådan begreppsförståelse eller att det är för svårt. Personligen håller jag inte med. Jag har alltid (även före CCS) strävat efter att förklara begreppen för bråkaritmetik så att eleverna inte slutar med att ”blint följa reglerna” och bara kan räkna med bråk om de råkar komma ihåg regeln korrekt. Jag har alltid betonat den konceptuella förståelsen i matematik (som mina läsare vet!).

Men jag hoppas att ni kan se hur en del av dessa saker kan vara obekanta för skollärare och föräldrar, och därför är det inte konstigt att det är svårt för dem att följa Common Core Standards.

Det är min förhoppning att Math Mammoth Light Blue Series och de enheter som jag säljer i mina Teachers Pay Teachers- och Teachers’ Notebook-butiker kan hjälpa de lärare & föräldrar som behöver Common Core-anpassat material. Och som jag sa, resten av er kan vara säkra på att använda dem också. De innehåller ingen ”konstig” eller meningslös matematik, utan är som alltid baserade på den solida grunden att lära ut matematiska begrepp tillsammans med procedurerna.

av Maria Miller