Eigenvärden är en speciell uppsättning skalarer som är associerade med ett linjärt ekvationssystem (i.e., en matrisekvation) som ibland också kallas karakteristiska rötter, karakteristiska värden (Hoffman och Kunze 1971), egentliga värden eller latenta rötter (Marcus och Minc 1988, s. 144).

Bestämningen av ett systems egenvärden och egenvektorer är ytterst viktig inom fysik och teknik, där den är likvärdig med diagonalisering av matriser och förekommer i så vanliga tillämpningar som stabilitetsanalys, fysiken hos roterande kroppar och små svängningar hos vibrerande system, för att nämna bara några. Varje egenvärde är parat med en motsvarande så kallad egenvektor (eller, i allmänhet, en motsvarande höger egenvektor och en motsvarande vänster egenvektor; det finns ingen analog distinktion mellan vänster och höger för egenvärden).

Den nedbrytning av en kvadratisk matris i egenvärden och egenvektorer kallas i detta arbete för egendekomposition, och det faktum att denna nedbrytning alltid är möjlig så länge den matris som består av egenvektorerna i är kvadratisk är känd som teoremet om egendekomposition.

Lanczos-algoritmen är en algoritm för beräkning av egenvärden och egenvektorer för stora symmetriska sparsamma matriser.

Låt vara en linjär transformation som representeras av en matris . Om det finns en vektor så att

(1)

för en viss skalär , så kallas för egenvärdet av med motsvarande (höger) egenvektor .

Låt vara en kvadratisk matris

(2)

med egenvärde , så uppfyller motsvarande egenvektorer

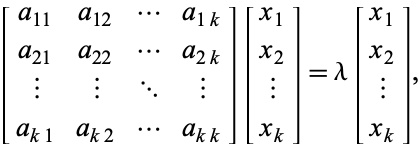(3)

vilket är ekvivalent med det homogena systemet

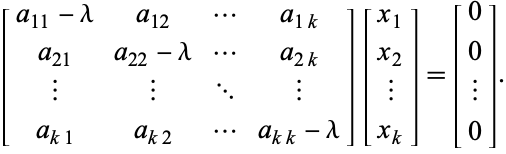(4)

Förutsättning (4) kan skrivas kompakt som

(5)

där är identitetsmatrisen. Som framgår av Cramers regel har ett linjärt ekvationssystem icke-triviala lösningar om determinanten försvinner, så lösningarna till ekvation (5) ges av

(6)

Denna ekvation är känd som den karakteristiska ekvationen för , och den vänstra sidan är känd som det karakteristiska polynomet.

Till exempel för en matris, är egenvärdena

(7)

vilket uppstår som lösningarna av karakteristicequation

(8)

Om alla egenvärden är olika, så ger det oberoende ekvationer för komponenterna i varje motsvarande egenvektor, och systemet sägs vara icke-degenererat. Om egenvärdena är -faldigt degenererade sägs systemet vara degenererat och egenvektorerna är inte linjärt oberoende. I sådana fall kan den ytterligare begränsningen att egenvektorerna ska vara ortogonala,

(9)

där är Kroneckerdeltaet, tillämpas för att ge ytterligare begränsningar, och på så sätt tillåta lösning för egenvektorerna.

Eigenvärden kan beräknas i Wolfram Language med hjälp av Eigenvalues. Egenvektorer och egenvärden kan returneras tillsammans med kommandot Eigensystem.

Antag att vi känner till egenvärdet för

(10)

Lägg till en konstant gånger identitetsmatrisen,

(11)

så de nya egenvärdena är lika med de gamla plus . Multiplicera med en konstant

(12)

så att de nya egenvärdena är lika med de gamla multiplicerat med .

Tänk nu på en likhetstransformation av . Låt vara determinanten för , då

			(13)
			(14)
			(15)

så egenvärdena är desamma som för .