
Galileo betraktas ofta som den moderna vetenskapens fader. Han var den som sammanförde principerna för experiment, teori och matematik till en standardiserad ram. Förmodligen mer än någon annan var Galileo den person som var ansvarig för utvecklingen av den moderna vetenskapen.
Det sägs att Galileo släppte två stålkulor med olika massa, men av samma material, från det lutande tornet i Pisa och att de landade vid samma tidpunkt. Det som är anmärkningsvärt med detta experiment är att han inledde en ny metod för att bedriva vetenskap där man utför ett experiment för att testa en hypotes. Han visade att vi måste göra mer än att bara tro att något är sant, utan vi måste också bevisa det.

Galileo fann en intressant paradox när han var chef för matematiska institutionen vid universitetet i Pisa.
Definition: En paradox, även kallad antinomi, är ett logiskt självmotsägelsefullt påstående eller ett påstående som går emot ens förväntningar. (Wikipedia). (Grekiska: ”para” = bortom, ”doxa” = tro)
Galileos paradox handlade om att avgöra om två uppsättningar som innehåller oändliga objekt är likvärdiga med varandra. Låt till exempel P vara mängden positiva heltal där P= {0,1,2,3,…} och E vara mängden jämna tal där E = {0,2,4,6,…}. Galilei hävdade att storleken på dessa två mängder kommer att vara densamma eftersom vi kan para ihop varje positivt heltal från mängden P med jämna tal från mängden E.

Hur kan då storleken på de två mängderna vara densamma när ett ”färre” tal förekommer i E? Detta kallades Galileos paradox och startade en ny debatt om begreppet oändlighet.
Efter Galileo blev hans elev Evangelista Torricelli chef för matematiska institutionen vid universitetet i Pisa. Du kanske har hört talas om honom på grund av hans arbeten om atmosfäriskt tryck och uppfinningen av barometern. Eftersom Toricelli också är intresserad av matematik frågar han:
Är det möjligt att ha ett föremål med en ändlig volym och en oändlig yta? För det första verkar en sådan sak osannolik för de flesta av oss. Matematiken talar dock om för oss att en sådan sak skulle kunna inträffa. Torricelli svarade själv på sin fråga och upptäckte Toricellis trumpet vars yta är oändlig men vars volym är ändlig. Hans upptäckt ses som en ”otrolig” paradox.
Förresten finns det en väsentlig regel inom matematikens filosofi; Oavsett vilken epok inom filosofi eller matematik du sysslar med så är den relaterad till historien, kulturen och religionen i den regionen. Det är därför man kallar Toricellis trumpet även för Gabriels horn. Här görs en hänvisning till Bibeln eftersom kristna tror att ängeln Gabriel kommer att blåsa i hornet på domedagen.
Hur formas då Toricellis trumpet? Vi vet alla hur man graferar y=x. Om man istället graferar ekvationen y=1/x där x är större eller lika med 1 kommer grafen att se ut så här:
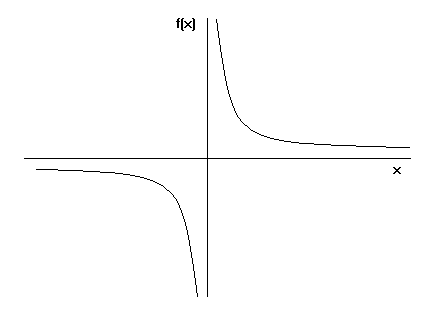
När vi tar grafen för y=1/x och roterar den runt x-axeln ser vi Toricellis trumpet.

Tursamt nog har vi matematiska formler i handen som gör att vi kan beräkna arean och volymen av Toricellis trumpet. När vi använder integrationsformeln nedan för trumpetens volym får vi en ändlig mängd.
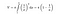
När vi däremot tillämpar integrationsformeln för trumpetens yta blir den här gången ytan på den oändlig. Är inte detta resultat intressant?
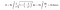
Då volymen på Toricellis trumpet är ändlig, kan vi fylla den med en ändlig mängd färg. Låt oss till exempel anta att volymen är 100 liter. Jag går till Home Depot och köper 100 liter färg och fyller den. Det som gör detta intressant är dock att jag kommer att ha målat den oändliga ytan med dessa 100 liter färg. Idag kallar de flesta människor denna paradox för ”målarparadoxen”
Houston, vi har ett problem här! Den situation som är omöjlig i praktiken blir möjlig i matematiken. Så hur kan Torricellis trumpet vara verklig? Eller hur kan vi exakt matcha alla element i mängderna samtidigt som en av mängderna är en delmängd av en annan i Galileos exempel?
Anledningen till alla dessa konflikter är att oändlighetsbegreppet inte liknar andra begrepp som vi känner till, och det förvirrar många människor. Galileo säger om sin paradox,
”Ja, min vän, det finns oändlighet. Det är meningslöst att invända mot det. De mängder jag arbetar med är exempel på slutna mängder som innefattar oändlighet. De börjar vid en punkt och fortsätter till oändligheten, och ändå är de fortfarande en uppsättning. Mina kommentarer och begrepp om oändligheten måste dock vara annorlunda än de jag skulle använda för ändliga storheter. Om man har att göra med ändliga storheter kan man säga att 3 kilo är mindre än 5 kilo, eller att 32 meter är längre än 7 meter. Men när det gäller oändlighet kan du inte säga att den här oändligheten är större, mindre eller lika med den.”
Det var Galileos lösning på 1600-talet.
Olyckligtvis hade Galileos lösning startat en ny debatt om oändlighet. Matematiker och filosofer kunde inte enas om ett specifikt svar förrän Cantor delade med sig av sin ”mängdteori”, som eleverna lär sig i grundskolan idag.
Vi kan periodvis historisera utvecklingen av idén om oändlighet. Den uppstod först hos Eleatikerna, som var en för-sokratisk filosofisk skola som grundades av Parmenides i början av det femte århundradet f.Kr. i den antika staden Elea. Det fanns tre stora filosofer inom denna skola, såsom Zeno, Xenofanes och Parmenides. I denna skola var den accepterade filosofin att tillvaron var singulär och att det inte fanns någon mångfald. Zeno var berömd för sina paradoxer om oändligheten hos de eleatiska. Senare på 300-talet f.Kr, Aristoteles uppstod och föreslog ett par begrepp för att förklara Zenos paradoxer, vilka var potentiell oändlighet och faktisk oändlighet.
Den potentiella oändligheten är en grupp av tal eller en grupp av ”saker” som fortsätter utan att avslutas, fortsätter eller upprepar sig om och om igen utan någon igenkännbar slutpunkt.
Den faktiska oändligheten innefattar aldrig upphörande uppsättningar eller ”saker” inom ett utrymme som har en början och ett slut; det är en serie som tekniskt sett är ”avslutad” men som består av ett oändligt antal medlemmar.
Aristoteles trodde att det inte fanns någon faktisk oändlighet. Denna idé från Aristoteles dominerade filosofins värld fram till 1600-talet. Då hävdade filosofer som Cusa och Bruno att det finns en faktisk oändlighet, men att vi inte kan förstå den. Efter Cusa och Bruno kom den store tänkaren Spinoza in i ämnet.
Spinoza sa att vi kan förstå begreppet oändlighet och rangordna dem i storlek. Men han sade också att han inte kunde räkna på dem. Till exempel kunde han addera 3 till 5, men han kunde inte addera en oändlighet till en annan.
För att avsluta dessa debatter dök slutligen en vacker man, Georg Cantor, upp och fann mängdteorin, som fortfarande är grunden för matematiken. Han satte den sista punkten i oändlighetsdiskussionerna med sin mängdteori.
Han visade oss att en oändlighetsmängd skulle vara större eller mindre än en annan oändlighetsmängd. Vidare hävdade Cantor att vi kunde addera och multiplicera oändlighetsmängder. Fram till dess hade människorna följt Aristoteles idéer om oändlighet. Enligt Aristoteles skulle talet 3, om vi multiplicerar det med oändligheten, bli oändligt igen. Oändligheten skulle svälja allting. Baserat på detta hävdade han att det bara skulle finnas en potentiell oändlighet, inte en faktisk oändlighet.
Cantor bevisade dock för oss motsatsen till Aristoteles idé med mängdteorin. Om vi lägger till en till en oändlig mängd kommer det inte längre att vara samma mängd. Han försökte jämföra oändligheterna. Cantor bevisade till exempel att mängden av alla funktioner från (0,1)→ℕ är räknbar. Således definierade han en en-till-en- och på-funktion från intervallet (0,1) till naturliga tal.
Med andra ord bevisade han att alla naturliga tal kan rymmas mellan 0 och 1 eftersom det fanns oändliga rationella tal mellan 0-1, och dessa oändligheter kan paras ihop. Sedan gjorde han något ännu farligare än att hitta två lika stora oändligheter. Han jämförde oändligheten av reella tal med oändligheten av naturliga tal och fann att oändligheten av reella tal är större än den andra. Han tittade till och med på sitt bevis och sa till sin vän Dedekind: ”Jag ser det, men inte ens jag kan tro det …”.
Cantor var också en matematiker med mycket allvarliga filosofiska och religiösa bekymmer. När han utvecklade mängdteorin sade han: ”Gud dikterade mig mängdteorin”.
Mängdteorin var inte allmänt accepterad när den först utvecklades. Företag anställde inte ens Cantor för något jobb. En matematiker, Henri Poincaré, sade en gång: ”Denna Cantors idéer är en dålig sjukdom som fastnar i matematikens krage. Och matematiken kommer att behandla honom en dag”. Cantor var tvungen att gå på mentalsjukhus ett tag och dog där. Men idag betraktar vi honom som ett geni.
Cantor var en ensam man på gränsen till oändligheten. Han citerade Bibeln i början av sin artikel om oändliga tal: ”Allt som är dolt kommer att komma fram i ljuset”
.