I månadstipset (TOTM) från november 2011 presenterade vi kompressorberäkningarna i en fallstudie. Vi jämförde resultaten från den rigorösa metoden med värdena från genvägsmetoderna. Den rigorösa metoden byggde på en tillståndsekvation som Soave-Redlich-Kwong (SRK) för att beräkna de erforderliga enthalpierna och entropierna. Enthalpierna och entropierna används för att bestämma effektbehovet och utloppstemperaturerna. Resultaten visade att noggrannheten hos genvägsmetoden är känslig för värdet på värmekapacitetsförhållandet i idealgastillstånd, k.
Enbart ur beräkningssynpunkt är effektberäkningen särskilt känslig för specifikationen av massflödeshastighet, sugtemperatur och sugtryck samt avlastningstemperatur och avlastningstryck. En kompressor kommer att fungera med varierande värden på de variabler som påverkar dess prestanda. Den svåraste delen av en kompressorberäkning är därför att specificera ett rimligt intervall för varje variabel och inte själva beräkningen. Referensen betonar att användning av ett enda värde för varje variabel inte är det korrekta sättet att utvärdera ett kompressorsystem.
Normalt utförs de termodynamiska beräkningarna för en ideal (reversibel) process. Resultaten för en reversibel process anpassas sedan till verkligheten genom användning av en termodynamisk effektivitet. I kompressionsprocessen finns det tre ideala processer som kan visualiseras: 1) en isotermisk process (PV1=C1), 2) en isentropisk process (PVk=C2) och 3) en polytropisk process (PVn=C3). Vilken som helst av dessa processer kan på lämpligt sätt användas som grund för att utvärdera kraven på kompressionseffekt genom antingen hand- eller datorberäkning. Den isotermiska processen används dock sällan som grund eftersom den normala industriella kompressionsprocessen inte ens tillnärmelsevis utförs vid konstant temperatur.
Notera att Dresser Rand gör en hel del arbete med kompression ”nära konstant temperatur”, särskilt för CO2-komprimering från ventilationsskorstenar. För detaljer hänvisas till:
I denna TOTM kommer vi att visa hur man bestämmer en kompressors effektivitet utifrån uppmätt flödeshastighet, sammansättning, sug- och utloppstemperaturer och tryck. En rigorös beräkning baserad på en tillståndsekvation och en genvägsmetod beaktas och resultaten jämförs.
Kompressoreffektivitet
Kompressoreffektiviteten varierar med kompressortyp, storlek och genomströmning. De kan endast bestämmas (i efterhand) genom ett kompressortest, även om kompressortillverkarna vanligtvis kan ge bra uppskattningar. För planeringsändamål föreslår referens följande värden för de totala efficierna:
Tabell 1. Totala kompressoreffektiviteter
|
Kompressortyp |
Effektivitet, η |
|
Centrifugal |
0.70 – 0,85 |
|
Höghastighetsväxlare |
0,72 – 0,85 |
|
Låghastighetsväxlare |
0.75 – 0,90 |
|
Rotary Screw |
0,65 – 0,75 |
Hänvisningen visar att dessa totala efficienser inkluderar gasfriktion inom kompressorn, de mekaniska förlusterna (lager, tätningar, växellåda etc.) och växellådsförluster. Den mekaniska efficiencyen varierar med kompressorstorlek och typ, men 95 % är ett användbart planeringsvärde. När man beräknar kompressorns tryckhöjd och utloppstemperatur kommer den efficiency som används att vara isentropisk eller polytropisk (isentropisk efficiency kallas ibland adiabatisk efficiency). Om man lägger till 3-4 % efficiency (mekaniska förluster) till de totala efficierna i tabell 1 får man i allmänhet en bra uppskattning av den termodynamiska efficiencen.
För att utvärdera prestandan hos en befintlig kompressor är målet att beräkna kompressoreffekten (η) och effektbehovet.
Kända och uppmätta egenskaper är:
a. Gasvolymflöde (qS) eller gasmassaflöde ()
b. Gassammansättning (zi)
c. Sugtryck (P1) och temperatur (T1)
d. Utsläppstryck (P2) och temperatur (T2)
Skattning av effektivitet – rigorös metod
Kärnan i varje kommersiell programvara för simulering av processflöden är en tillståndsekvation. På grund av deras enkelhet och relativa noggrannhet används en kubisk EOS såsom Soave Redlich-Kwong (SRK) eller Peng-Robinson. Dessa ekvationer används för att beräkna Vapor-Liquid-Equilibria (VLE), entalpi (h) och entropi (s). Med korrekta binära interaktionskoefficienter är processsimuleringsresultaten från dessa två ekvationer praktiskt taget desamma. Därför används endast SRK i detta arbete.
Den isentropiska verkningsgraden definieras genom
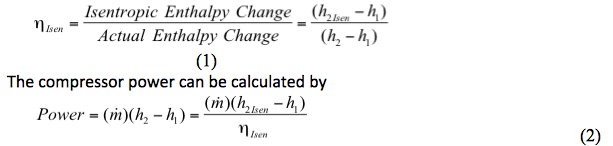
Varvid:
ηIsen = Isentropisk verkningsgrad
h1 = Sugentalpi beräknad vid P1, T1 och sammansättning (zi)
h2 = Utsläppsentalpi beräknad vid P2, T2, och sammansättning (zi)
h2Isen = Isentropisk utloppsenthalpi vid P2 (eller T2), S2Isen =S1, och sammansättning (zi)
![]() = Massflödeshastighet
= Massflödeshastighet
Beräkningen av kompressoreffektivitet eller effekt omfattar två steg
1. Bestämning av den ideala eller isentropiska (reversibla och adiabatiska) entalpiändringen (h2Isen-h1) för kompressionsprocessen.
2. Bestämning av den faktiska entalpiändringen (h2-h1).
Den stegvisa beräkningen som bygger på en EOS:
a. Anta stationärt tillstånd, dvs.
b. Anta att fodersammansättningen förblir oförändrad
c. Beräkna sugningsenthalpin h1=f(P1, T1 och zi) och entropin s1=f(P1, T1 och zi) med EOS
d. Anta en isentropisk process och ställ in s2Isen = f (P2, T2Isen, zi) = s1 = f (P1, T1, zi).
e. Beräkna den ideala entalpen (h2Isen) vid utloppstillstånd för kända zi, T2 (eller P2) och s2Isen.
f. Beräkna den faktiska entalpinivån (h2) vid utloppstillståndet för kända zi, T2 och P2.
g. Beräkna den isentropiska verkningsgraden med hjälp av ekvation 1: µIsen = (h2Isen – h1)/(h2 – h1)
h. Beräkna effekten med ekvation 2: ![]()
Skattning av effektivitet – kortfattad metod
Exponenten för isentropisk väg (k) eller värmekapacitetsförhållandet för ideala gaser (k=CP/CV) kan beräknas med hjälp av den korrelation som presenterades i TOTM från maj 2013:
![]()
Var:
T = Temperatur, K (°R)
![]() = Gasens relativa densitet; förhållandet mellan gasens molekylvikt och luftens molekylvikt
= Gasens relativa densitet; förhållandet mellan gasens molekylvikt och luftens molekylvikt
A = 0.000272 (0.000151)
Den faktiska utloppstemperaturen baserad på en isentropisk väg kan uppskattas genom

Lösning av den isentropiska verkningsgraden,
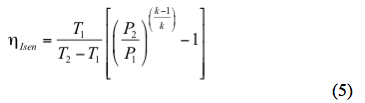
Samma sak, kan den faktiska utloppstemperaturen baserad på en polytropisk väg uppskattas genom att

lösas med ovanstående ekvation för koefficienten för den polytropiska vägen (n):

På samma sätt kan den faktiska utloppstemperaturen baserad på en polytropisk bana uppskattas (ηPoly) genom:

Den isentropiska höjden beräknas genom
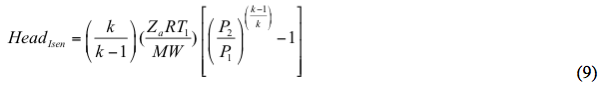
Samma sak, beräknas den polytropa huvudet med
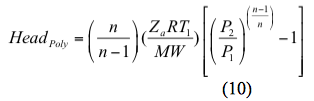
För en isentropisk (reversibel och adiabatisk) process beräknas effekten med
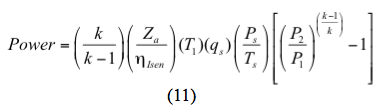
Och för en polytropisk process beräknas effekten med
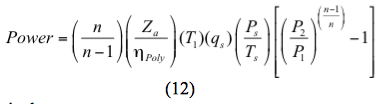
Alternativt:
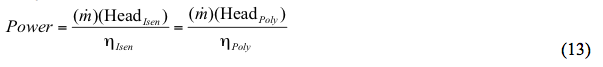
Var:
Head = Kompressorhöjd, m (ft)
Power = Kompressoreffekt, kW (HP)
R = Universell gaskonstant, 848 kg-m/(kmol-K) eller (1545 ft-lbf/(lbmol-°R))
PS = Standardtryck, kPa (psia)
P1 = Sugtryck, kPa (psia)
P2 = Utloppstryck, kPa (psia)
TS = Standardtemperatur, K (°R)
T1 = Sugtemperatur, K (°R)
T2 = Utloppstemperatur, K (°R)
qS = Gasvolymvolym vid standardförhållande, Sm3/d (scf/dag)
Za = Genomsnittlig komprimerbarhetsfaktor för gasen = (Z1+Z2)/2
Z1 = Komprimerbarhetsfaktor för gasen vid sugförhållande
Z2 = Komprimerbarhetsfaktor för gasen vid utloppsförhållande
MW = Gasens molekylvikt
Effektberäkningen ska göras per komprimeringssteg och sedan summeras för alla steg som är anslutna till en enda drivrutin.
Steg-för-steg-beräkningen för genvägsmetoden
a. Beräkna den isentropiska exponenten (k) med ekvation 3 med hjälp av medeltemperaturen definierad genom T = (T1+3T2)/4. Denna form av medeltemperatur definierades för att få bättre överensstämmelse mellan de rigorösa resultaten och resultaten från förkortningsmetoden.
b. Beräkna den isentropiska effektiviteten (ηIsen) med hjälp av ekvation 5.
c. Beräkna den polytropiska koefficienten (n) med ekvation 7.
d. Beräkna den polytropiska effektiviteten (ηPoly) med hjälp av ekvation 8.
e. Beräkna de isentropiska och polytropiska huvudena med hjälp av ekvation 9 respektive 10.
f. Beräkna den erforderliga effekten per steg med hjälp av antingen ekvation 11 eller 12.
Fallstudie
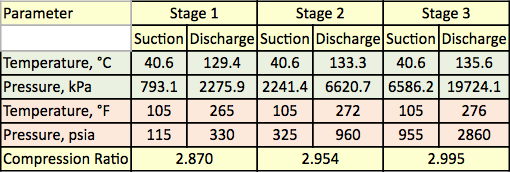
En naturgasblandning komprimeras med hjälp av en trestegs centrifugalkompressor. Processflödesdiagrammet visas i figur 1. För varje steg presenteras det uppmätta trycket och temperaturen i tabell 1. Den uppmätta matningssammansättningen, flödeshastigheterna och den beräknade molekylvikten och relativa densiteten presenteras i tabell 2.
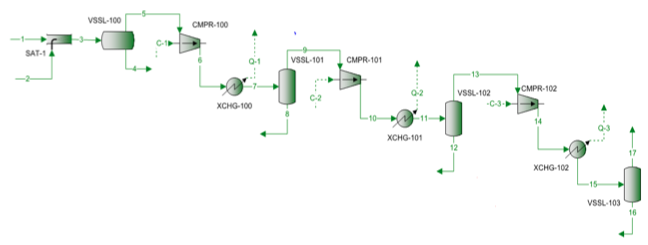
Figur 1. Processflödesdiagram för en trestegskompression
Tabell 1. Uppmätt temperatur och tryck för de tre kompressionsstegen
Tabell 2. Gasanalys och flödeshastighet för de tre kompressionsstegen
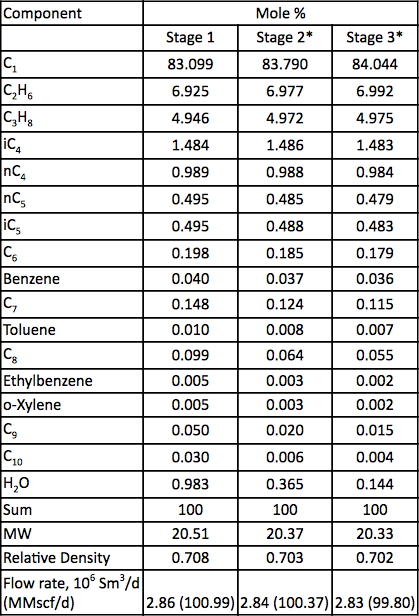
* Beräknat
Resultat och diskussioner
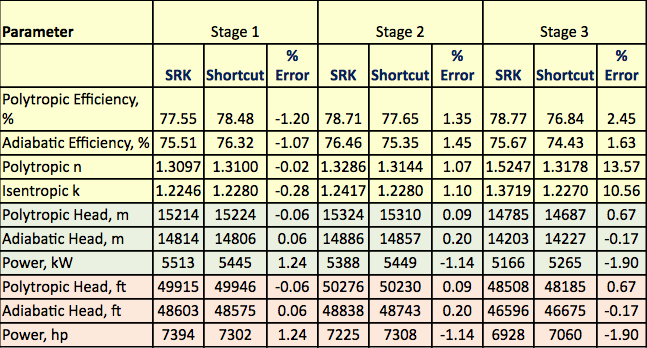
Processflödesdiagrammet som visas i figur 1 simulerades med ProMax-programvaran för att utföra de rigorösa beräkningarna med SRK EOS. Programmet beräknade polytropisk och isentropisk verkningsgrad, huvuden och kompressionseffekt. Programmet beräknade också exponenten för isentropisk väg (k) och exponenten för polytropisk väg (n). Dessa beräknade resultat presenteras i tabell 2 för alla tre stegen under SRK-rubriker. De beräkningar som utförs av ProMax är mycket lika de stegvisa beräkningarna av a till h som beskrivs i det rigorösa avsnittet. I tabell 2 presenteras också de kortfattade beräkningsresultaten för motsvarande värden under den kortfattade rubriken. De korta beräkningarna är baserade på de stegvisa beräkningarna av a till f som beskrivs i avsnittet om kortfattad metod. Felprocenten mellan den rigorösa metoden och de korta metoderna för varje steg presenteras också i tabell 2. Tabell 2 visar att utmärkta överensstämmelser erhålls för etapperna 1 och 2. Större avvikelser observeras dock för de isetropiska och polytropiska exponenterna för steg 3 på grund av högtrycksdrift som avviker för mycket från de ideala gastillståndsförhållandena.
Tabell 3. Sammanfattning av de rigorösa och genvägsberäknade resultaten
Slutsatser
Tabell 2 visar att det finns goda överensstämmelser mellan de genvägsberäknade och de rigorösa resultaten. Skillnaderna mellan de rigorösa resultaten och resultaten från förkortningsmetoden för anläggningsberäkningar och planeringsändamål är försumbara. För steg 3 observeras ett större fel för den isentropiska exponenten (k) på grund av högtrycksdrift och för stora avvikelser från det ideala gastillståndstillståndet.
Den beräknade isentropiska exponenten (k) i ProMax är inte det ideala gastillståndsförhållandet för värmekapaciteten (CP/CV). Det är värdet på den isentropiska exponenten som krävs för att ge en isentropisk väg från inlopp till utlopp. Dess värde beräknas som en integration av denna väg. Det är alltså i viss mån ett ”medelvärde” som representerar den verkliga isentropiska vägen. För idealiska gaser skulle värdet vara lika med förhållandet (CP/CV).
Detta fel i ”k” illustrerar också vikten av att specificera vilken korrelation som ska användas när man beställer ett prestandaprov (se ASME PTC-10 för ytterligare detaljer), så att kunden och leverantören är överens om molekylvikt (MW) och k för provningsvätskan. För ytterligare detaljer hänvisas till referens och TOTM från augusti och september 2010 .
Det kan också vara värt att notera att när man försöker utvärdera maskinkonditionen med hjälp av trender för ”n” och den polytropa verkningsgraden, så medför den relativa noggrannheten hos mätinstrumenten/utrustningen (temperatur- och tryckgivare) och kartläggningen av kompressorns prestanda till den ursprungliga prestandakurvan (faktiskt gasvolymflöde i förhållande till varvtalet), att det införs många potentiella felkällor i den dagliga utvärderingen.
Notera att noggrannheten hos förkortningsmetoderna är beroende av värdena för k och n. Definitionen av medeltemperatur i förkortningsmetoden justerades för att få en bättre överensstämmelse mellan exponenten för isentropisk väg (k) beräknad med rigorös metod.
Om du vill veta mer om liknande fall och hur man minimerar driftsproblem föreslår vi att du deltar i våra kurser G4 (Gaskonditionering och bearbetning), PF4 (Oljeproduktions- och bearbetningsanläggningar), ME46 (Kompressorsystem – Mekanisk konstruktion och specifikationer) och ME44 (Grunderna för pump- och kompressorsystem).
PetroSkills erbjuder konsultkompetens i detta ämne och många andra. För mer information om dessa tjänster, besök vår webbplats på http://petroskills.com/consulting, eller mejla oss på [email protected].
Dr. Mahmood Moshfeghian
Referens:
3. Soave, G., Chem. Eng. Sci., Vol. 27, pp. 1197-1203, 1972.
4. Peng, D. Y., and Robinson, D. B., Ind. Eng. Chem. Fundam., Vol. 15, s. 59, 1976.
5. ProMax 3.2, Bryan Research and Engineering, Inc, Bryan, Texas, 2014.
6. ASME PTC-10, ”Performance test Code on Compressors and Exhausters”, 1997.
7. Honeywell, J. ”Important Aspects of Centrifugal Compressor Testing-Part 1”, Månadens tips, augusti 2010
8. Honeywell, J. ”Important Aspects of Centrifugal Compressor Testing-Part 2”, Månadens tips, september 2010
.