Likt P-Only-regulatorn beräknar och sänder PI-algoritmen (Proportional-Integral) en signal för utmatning av regulatorn (CO) vid varje provtagningstillfälle, T, till det slutliga styrelementet (t.ex. en ventil eller en pump med variabelt varvtal). Den beräknade CO-signalen från PI-algoritmen påverkas av styrenhetens inställningsparametrar och styrenhetens fel, e(t).
PI-regulatorer har två inställningsparametrar att justera. Även om detta gör dem mer utmanande att ställa in än en ren P-regulator är de inte lika komplexa som PID-regulatorn med tre parametrar.
Integral verkan gör det möjligt för PI-regulatorer att eliminera förskjutning, vilket är en stor svaghet hos en ren P-regulator. PI-regulatorer ger således en balans mellan komplexitet och kapacitet som gör dem till den överlägset mest använda algoritmen i processkontrolltillämpningar.
PI-algoritmen
Om olika leverantörer har gett samma algoritm olika former, utforskar vi här det som på olika sätt beskrivs som den beroende, ideala, kontinuerliga, positionella formen:
![]()
Var:
CO = styrenhetens utsignal (kabeln ut)
CObias = styrenhetens bias eller nollvärde; inställd genom stöppfri överföring som förklaras nedan
e(t) = aktuellt reglerfel, definierat som SP – PV
SP = börvärde
PV = uppmätt processvariabel (ledningen in)
Kc = reglerförstärkning, en inställningsparameter
Ti = nollställningstid, en inställningsparameter
De två första termerna till höger om likhetstecknet är identiska med P-Only-regulatorn som det hänvisas till högst upp i den här artikeln.
Regulatorns integralläge är den sista termen i ekvationen. Dess funktion är att integrera eller kontinuerligt summera regulatorfelet, e(t), över tiden.
Några saker vi bör veta om inställnings parametern för återställningstid, Ti:
| ▪ | Den ger en separat vikt till integraltermen så att påverkan av den integrala åtgärden kan justeras oberoende av varandra. |
| ▪ | Den finns i nämnaren så att mindre värden ger en större vikt till (dvs. ökar inflytandet av) den integrala termen. |
| ▪ | Den har tidsenheter så den är alltid positiv. |
Funktionen hos den proportionella termen
Som med den rena P-regulatorn lägger den proportionella termen i PI-regulatorn, Kc-e(t), till eller drar ifrån CObias baserat på storleken på regulatorfelet e(t) vid varje tidpunkt t.
När e(t) växer eller krymper, växer eller krymper den mängd som läggs till CObias omedelbart och proportionellt. Regulatorfelets tidigare historia och nuvarande bana har ingen inverkan på beräkningen av den proportionella termen.
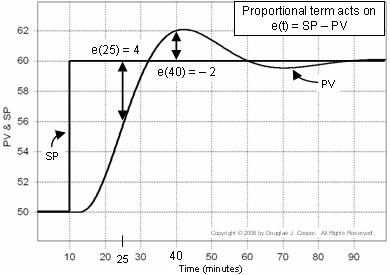
Plotten nedan (klicka för en större bild) illustrerar denna idé för en setpointrespons. Felet som används i den proportionella beräkningen visas i diagrammet:
▪ Vid tiden t = 25 min, e(25) = 60-56 = 4
▪ Vid tiden t = 40 min, e(40) = 60-62 = -2
Med tanke på att reglers fel e(t) = SP – PV, snarare än att betrakta PV och SP som separata spår som vi gör ovan, kan vi beräkna och plotta e(t) vid varje punkt i tiden t.
Nedan (klicka för en större bild) visas identiska data som ovan, men de är omformade till en plott av e(t) själv. Lägg märke till att i diagrammet ovan är PV = SP = 50 för de första 10 minuterna, medan i feldiagrammet nedan är e(t) = 0 för samma tidsperiod.
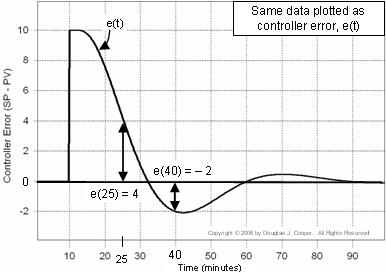
Detta diagram är användbart eftersom det hjälper oss att visualisera hur felet i regulatorn kontinuerligt ändrar storlek och tecken när tiden går.
Funktionen hos den integrala termen
Medan den proportionella termen tar hänsyn till den aktuella storleken på e(t) endast vid tidpunkten för regulatorns beräkning, tar den integrala termen hänsyn till felets historik, eller hur länge och hur långt den uppmätta processvariabeln har legat från börvärdet över tiden.
Integration är en kontinuerlig summering. Integrering av felet över tiden innebär att vi summerar hela felhistoriken för regulatorn fram till den aktuella tidpunkten, med början när regulatorn först ställdes om till automatik.
Regulatorns fel är e(t) = SP – PV. I diagrammet nedan (klicka för en större bild) beräknas integralsumman av felet som de skuggade områdena mellan SP- och PV-spåren.
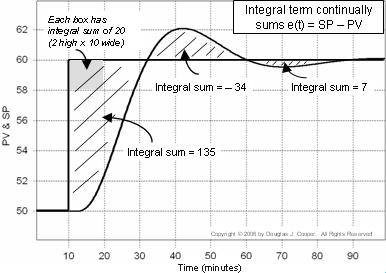
Varje ruta i diagrammet har en integralsumma på 20 (2 höga gånger 10 breda). Om vi räknar antalet rutor (inklusive bråkdelar av rutor) som ingår i de skuggade områdena kan vi beräkna den integrala felsumman.
Så när PV först passerar setpointen omkring t = 32 har den integrala summan vuxit till ungefär 135. Vi skriver PI-regulatorns integralterm som:
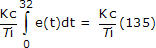
Då det är regulatorfelet som styr beräkningen får vi en direkt bild av situationen genom en plot av regulatorfelet enligt nedan (klicka för en större bild):

Bemärk att integralen för varje skuggat område har samma tecken som felet. Eftersom integralsumman börjar ackumuleras när regulatorn först sätts i automatik, växer den totala integralsumman så länge e(t) är positiv och krymper när den är negativ.
Vid tiden t = 60 min på plottarna är integralsumman 135 – 34 = 101. Svaret är i stort sett utjämnat vid t = 90 min, och integralsumman är då 135 – 34 + 7 = 108.
Integralverkan eliminerar offset
I föregående mening görs en subtil men mycket viktig observation. Svaret är i stort sett färdigt vid tiden t = 90 min, men ändå är integralsumman av alla fel inte noll.
I det här exemplet har integralsumman ett slut- eller restvärde på 108. Det är detta restvärde som gör det möjligt för PI-regulatorns integralverkan att eliminera offset.
Som diskuterats i en tidigare artikel upplever de flesta processer med enbart P-reglering offset under normal drift. Offset är ett uthålligt värde för reglerfel (dvs. PV är inte lika med SP vid steady state).
Vi känner igen från P-Only-regulatorn:
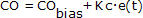
att CO alltid kommer att vara lika med CObias om vi inte adderar eller subtraherar något från det.
Det enda sättet som vi har något att addera eller subtrahera från CObias i P-Only-ekvationen ovan är om e(t) inte är noll. Om e(t) inte är konstant noll är PV inte lika med SP och vi har en förskjutning.
Med PI-regulatorn:
![]()
Vi vet nu att den integrerade felsumman kan ha ett slut- eller restvärde efter det att ett svar är klart. Detta är viktigt eftersom det innebär att e(t) kan vara noll, men att vi ändå kan ha något att addera eller subtrahera från CObias för att bilda den slutliga reglerutgången, CO.
Så länge det finns något fel (så länge e(t) inte är noll), kommer integraltermen att växa eller krympa i storlek för att påverka CO. Förändringarna i CO upphör först när PV är lika med SP (när e(t) = 0) under en längre tidsperiod.
Då kan den integrala termen ha ett restvärde som just diskuterats. Detta restvärde från integrationen, när det läggs till CObias, skapar i huvudsak ett nytt övergripande biasvärde som motsvarar den nya driftnivån.
I själva verket återställer integralverkan kontinuerligt biasvärdet för att eliminera förskjutning när driftnivån ändras.
Utmaningar med PI-reglering
Det finns utmaningar med att använda PI-algoritmen:
| ▪ | De två inställningsparametrarna interagerar med varandra och deras inflytande måste balanseras av konstruktören. |
| ▪ | Integritetstermen tenderar att öka det oscillerande eller rullande beteendet hos processresponsen. |
Då de två avstämningsparametrarna interagerar med varandra kan det vara utmanande att komma fram till ”bästa” avstämningsvärden. Värdet och betydelsen av vårt konstruktions- och inställningsrecept ökar när regulatorn blir mer komplex.
Initialisering av regulatorn för rumplös överföring
När vi växlar en regulator från manuellt läge till automatiskt läge (från öppen slinga till sluten slinga) vill vi att resultatet ska vara händelselöst. Det vill säga, vi vill inte att övergången ska orsaka plötsliga regleråtgärder som påverkar eller stör vår process
Vi uppnår detta önskade resultat vid övergången genom att initialisera regulatorns integralfelssumma till noll. Dessutom initialiseras börvärdet och reglersbiasvärdet genom att ställa in:
▪ SP lika med det aktuella PV
▪ CObias lika med det aktuella CO
Med felintegralsumman inställd på noll finns det inget att lägga till eller dra ifrån CObias som skulle kunna orsaka en plötslig förändring av den aktuella reglersignalen. Eftersom börvärdet är lika med den uppmätta processvariabeln finns det inget fel som kan driva en förändring av vår CO. Och med regulatorns bias inställd på vårt nuvarande CO-värde är vi som standard beredda att bibehålla den nuvarande driften.
När vi byter från manuellt läge till automatiskt har vi alltså en ”obegränsad överföring” utan överraskningar. Detta är ett resultat som alla uppskattar.
Reset Time Versus Reset Rate
Olika leverantörer kastar sina kontrollalgoritmer i lite olika former. Vissa använder proportionellt band i stället för reglerförstärkning. Vissa använder också återställningshastighet, Tr, i stället för återställningstid. Dessa är helt enkelt inversa av varandra:
Tr = 1/Ti
Oavsett hur inställningsparametrarna uttrycks är PI-algoritmerna alla lika kapabla.
Men det är viktigt att känna till din tillverkare innan du börjar ställa in din regulator eftersom parametervärdena måste anpassas till just din algoritmform.Kommersiell programvara för styrdimensionering och inställning kommer automatiskt att lösa detta problem åt dig.
Implementering av en PI-regulator
Vi utforskar PI-regulatorns utformning, inställning och implementering på värmeväxlaren i den här artikeln och på de gravitationsdränerade tankarna i den här artikeln.