Föreställ dig en fyrkant av papper som ligger platt på ditt skrivbord. Jag ber dig att blunda. Du hör hur pappret flyttas. När du öppnar ögonen verkar pappret inte ha förändrats. Vad kan jag ha gjort med det medan du inte tittade?

Det är uppenbart att jag inte har roterat pappret med 30 grader, för då skulle pappret se annorlunda ut.

Jag har inte heller vridit det tvärs över en linje som förbinder, låt oss säga, ett av hörnen med mitten av en annan kant. Pappret skulle se annorlunda ut om jag hade gjort det.

Vad jag däremot hade kunnat göra var att vrida pappret med eller moturs med en valfri multipel av 90 grader, eller att vända det tvärs över någon av de diagonala linjerna eller de horisontella och vertikala linjerna.

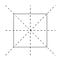
Ett bra sätt att visualisera omvandlingarna är att markera hörnen på kvadraten.

Det sista alternativet är att inte göra någonting. Detta kallas för identitetsomvandling. Tillsammans kallas alla dessa för kvadraternas symmetritransformationer.

Jag kan kombinera symmetritransformationer för att göra andra symmetritransformationer. Till exempel ger två vändningar över linjesegmentet BD identiteten, liksom fyra på varandra följande 90 graders rotationer moturs. En vändning om den vertikala linjen följt av en vändning om den horisontella linjen har samma säkra effekt som en 180 graders rotation. I allmänhet ger varje kombination av symmetriomvandlingar en symmetriomvandling. Följande tabell ger reglerna för sammansättning av symmetritransformationer:

I denna tabell betecknar R med substitut 90, 180 och 270 rotationer moturs med 90, 180 och 270 grader, H betyder en vändning om den horisontella linjen, V är en vändning om den vertikala linjen, MD är en vändning om diagonalen från övre vänstra till nedre högra sidan, och OD betyder en vändning över den andra diagonalen. För att hitta produkten av A och B går du till raden för A och sedan över till kolumnen för B. Till exempel: H∘MD=R₉₀.

Det finns några saker som du kan lägga märke till när du tittar på tabellen:

• Operationen ∘ är associativ, vilket innebär att A∘(B∘C) = (A∘B)∘C för alla transformationer A, B och C.
• För varje par av symmetritransformationer A och B är kompositionen A∘B också en symmetritransformation
• Det finns ett element e så att A∘e=e∘A för varje A
• För varje symmetritransformation A, finns det en unik symmetritransformation A-¹ så att A∘A-¹=A-¹∘A=e

Vi säger därför att samlingen av symmetritransformationer av en kvadrat, i kombination med komposition, bildar en matematisk struktur som kallas en grupp. Denna grupp kallas D₄, dihedralgruppen för kvadraten. Dessa strukturer är ämnet för denna artikel.

• Definition av en grupp
• Gruppens struktur
• Finita grupper är ändligt genererade
• Felresistent kommunikation
• Slutanmärkningar

Definition av en grupp

En grupp ⟨G,*⟩ är en mängd G med en regel * för att kombinera två element i G som uppfyller gruppaxiomen:

I abstrakt text undertrycker vi ofta * och skriver a*b som ab och hänvisar till * som multiplikation.

Det är inte nödvändigt att * är kommutativt, vilket innebär att a*b=b*a. Du kan se detta genom att titta på tabellen för D₄, där H∘MD=R₉₀ men MD∘H=R₂₇₀. Grupper där * är kommutativ kallas abeliska grupper efter Neils Abel.

Abeliska grupper är undantag snarare än regel. Ett annat exempel på en icke-abelisk grupp är symmetritransformationerna av en kub. Betrakta bara rotationer runt axlarna:

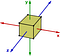
Om jag först roterar 90 grader moturs om y-axeln och sedan 90 grader moturs om z-axeln så får han ett annat resultat än om jag roterar 90 grader om z-axeln och sedan 90 grader om y-axeln.

Det är möjligt för ett element att vara sin egen inversa. Betrakta gruppen som består av 0 och 1 med operationen binär addition. Dess tabell är:

Det är tydligt att 1 är sin egen invers. Detta är också en abelisk grupp. Oroa dig inte, de flesta grupper är inte så här tråkiga.

Några fler exempel på grupper är:

• Mängden heltal med addition.
• Mängden rationella tal som inte innehåller 0 med multiplikation.
• Mängden lösningar till polynomekvationen xⁿ-1=0, som kallas för n:e rötterna av en enhet, med multiplikation.

Här är några exempel som inte är grupper:

• Mängden naturliga tal under addition är inte en grupp eftersom det inte finns några inverser, vilket skulle vara de negativa talen.
• Mängden av alla rationella tal inklusive 0 med multiplikation är inte en grupp eftersom det inte finns något rationellt tal q för vilket 0/q=1, så inte varje element har en invers.

Gruppens struktur

En grupp är mycket mer än bara en klump som uppfyller de fyra axiomen. En grupp kan ha en inre struktur, och denna struktur kan vara mycket invecklad. Ett av de grundläggande problemen i abstrakt algebra är att bestämma hur en grupps inre struktur ser ut, eftersom de grupper som faktiskt studeras i verkligheten är mycket större och mer komplicerade än de enkla exempel som vi har gett här.

En av de grundläggande typerna av inre struktur är en undergrupp. En grupp G har en undergrupp H när H är en delmängd av G och:

• För a,b∈H, a*b∈H och b*a∈H
• För a∈H, a-¹∈H
• Den identiska identiteten är ett element i H

Om H≠G så sägs H vara en korrekt undergrupp. Den undergrupp till G som endast består av identiteten kallas den triviala undergruppen.

En icke-abelisk grupp kan ha kommutativa undergrupper. Betrakta den kvadratiska dihedralgruppen som vi diskuterade i inledningen. Denna grupp är inte abelisk men rotationsundergruppen är abelisk och cyklisk:

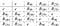
Vi ger nu två exempel på gruppstruktur.

Även om en grupp G inte är abelisk kan det ändå vara så att det finns en samling element i G som kommuterar med allt i G. Denna samling kallas G:s centrum. Centrum C är en undergrupp till G. Bevis:

Antag nu att f är en funktion vars domän och område båda är G. En period till f är ett element a∈G så att f(x)=f(ax) för alla x∈G. Mängden P av perioder av f är en undergrupp till G. Bevis:

Finita grupper är ändligt genererade

Vi såg att cykliska grupper genereras av ett enda element. När det är möjligt att skriva varje element i en grupp G som produkter av en (inte nödvändigtvis korrekt) delmängd A av G så säger vi att A genererar G och skriver detta som G=⟨A⟩. Det mest ”jaha, duh”-bevis du någonsin kommer att se är beviset för att alla ändliga grupper genereras av en ändlig genererande mängd:

• Låt G vara ändlig. Varje element i G är en produkt av två andra element i G så G=⟨G⟩. QED.

Vi avslutar den här artikeln med en tillämpning.

Felresistent kommunikation

Det enklaste sättet att överföra digital information är att koda den i binära strängar av fast längd. Inget kommunikationssystem är helt fritt från störningar, så det finns alltid en möjlighet att fel data tas emot. Metoden för avkodning med maximal sannolikhet är ett enkelt och effektivt sätt att upptäcka och korrigera överföringsfel.

Låt 𝔹ⁿ vara mängden binära strängar, eller ord, av längd n. Det är enkelt att visa att 𝔹ⁿ är en abelisk grupp under binär addition utan bäring (så att till exempel 010+011=001). Observera att varje element är sin egen invers. En kod C är en delmängd av 𝔹ⁿ. Följande är ett exempel på en kod i 𝔹⁶:

C = {000000, 001011, 010110, 011101, 100101, 101110, 110011, 111000}

Elementen i en kod kallas kodord. Endast kodord kommer att överföras. Ett fel sägs uppstå när störningar ändrar en bit i ett överfört ord. Avståndet d(a,b) mellan två kodord a och b är antalet siffror i vilka två kodord skiljer sig åt. Det minsta avståndet för en kod är det minsta avståndet mellan två av dess kodord. För exempelkoden precis ovan är det minsta avståndet tre.

I metoden för avkodning med maximal sannolikhet, om vi tar emot ett ord x, som kan innehålla fel, ska mottagaren tolka x som kodordet a så att d(a,x) är ett minimum. Jag kommer att visa att för en kod med minsta avstånd m kan detta alltid (1) upptäcka fel som ändrar färre än m bitar och (2) korrigera fel som ändrar ½(m-1) eller färre bitar.

I vår exempelkod är m=3 och sfären med radie ½(m-1)=1 kring kodordet 011101 är {011101, 11111101, 001101, 011001, 010101, 011111, 011100}. Så om mottagaren tar emot något av dessa ord vet den att det var meningen att den skulle ta emot 011101.

Så det är allt gott och väl, men vad har något av detta att göra med gruppteori? Svaret ligger i hur vi faktiskt producerar de koder som den här metoden arbetar med.

Det är möjligt för en kod i 𝔹ⁿ att bilda en undergrupp. I detta fall säger vi att koden är en gruppkod. Gruppkoder är ändliga grupper så de är ändligt genererade. Vi kommer att se hur man framställer en kod genom att hitta en genererande mängd.

En kod kan specificeras så att de första bitarna i varje kodord kallas informationsbitar och bitarna i slutet kallas paritetsbitar. I vår exempelkod C är de tre första bitarna informationsbitar och de tre sista är paritetsbitar. Paritetsbitarna uppfyller paritetskontrollsekvationerna. För ett kodord A₁A₂A₃A₄A₅A₆ är paritetsekvationerna A₄=A₁+A₂, A₅=A₂+A₃ och A₆=A₁+A₃. Paritetsekvationer ger ytterligare ett skydd mot fel: om någon av paritetsekvationerna inte är uppfylld har ett fel inträffat.

Här är vad vi gör. Anta att vi vill ha kodord med m informationsbitar och n paritetsbitar. För att generera en gruppkod skriver du en matris med m rader och m+n kolumner. I det block som bildas av de första m kolumnerna skriver du m×m identitetsmatrisen. I kolumn j för m+1≤j≤m_n, skriv en 1 i den k:e raden om Aₖ förekommer i paritetsekvationen för paritetsbiten Aⱼ och 0 annars. I vår exempelkod är matrisen:

En sådan matris kallas en genererande matris för gruppkoden. Du kan direkt verifiera att raderna genererar C:

Raderna i en genererande matris bildar en genererande mängd för en gruppkod C. Bevis:

• Identitet och inverser: Varje rad som adderas till sig själv ger identiteten, en sträng som består av alla nollor.
• Slutning: Om A,B∈C så är A och B summor av rader i den genererande matrisen så A+B är också en summa av rader i den genererande matrisen. Därför är A+B∈C.

Detta låter oss generera en kod, nu ska jag visa hur man genererar en användbar kod.

Definiera vikten w(x) så att den betyder antalet ettor i x. Till exempel w(100101)=3. Det är uppenbart att w(x)=d(x,0) där 0 är ett ord vars siffror alla är nollor. Den minsta vikten W för en kod är vikten för det kodord som inte är noll och som har minst ettor i koden. För en kod med minsta avstånd m är d(x,0)≥m så w(x)≥m och därför är W=m.

Hålls i minnet att för att ett ord ska betraktas som ett kodord måste det uppfylla en uppsättning paritetskontrollsekvationer. För vår exempelkod är dessa A₄=A₁+A₂, A₅=A₂+A₃ och A₆=A₁+A₃. Vi kan också skriva dessa som ett linjärt system:

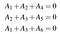
som i sin tur kan skrivas i termer av punktprodukter:

Och i mer kompakt form som Ha=0 där a=(A₁,A₂,A₃,A₄,A₅,A₆) och H är paritetskontrollmatrisen för koden:

Det går att verifiera genom direkt beräkning att om w(a)≤2 så kan vi inte ha Ha=0. I allmänhet är den minsta vikten t+1 där t är det minsta talet så att en samling av t kolumner i H inte summerar till noll (dvs. de är linjärt oberoende). Att bevisa detta skulle föra oss bara lite för långt in i linjär algebra.

Om detta skrämmer dig behöver du inte oroa dig. Vi kan producera några mycket bra koder utan det genom att dra nytta av det faktum att det resultat jag nyss nämnde innebär att om varje kolumn i H är icke-noll och inga två kolumner är lika så är den minsta vikten, och därmed det minsta avståndet för koden, minst tre. Detta är mycket bra: Om vårt kommunikationssystem förväntas ha ett bitfel för varje hundra överförda ord, så kommer endast ett av tio tusen överförda ord att ha ett okorrigerat fel och ett av en miljon överförda ord kommer att ha ett oupptäckt fel.

Så nu har vi ett recept för att framställa en användbar kod för detektionsschemat med maximal sannolikhet för kodord som innehåller m informationsbitar och n paritetsbitar:

• Skapa en matris med m+n kolumner och n rader. Fyll matrisen med ettor och nollor så att inga två kolumner är lika och ingen kolumn bara består av nollor.
• Varje rad i den resulterande paritetskontrollmatrisen motsvarar en av paritetsbitsekvationerna. Skriv dem som ett ekvationssystem och lös dem så att varje paritetsbit skrivs i termer av informationsbitarna.
• Skapa en matris med m+n kolumner och m rader. I det block som bildas av de första m kolumnerna skriver du m×m identitetsmatrisen. I kolumn j för m+1≤j≤m_n, skriv en 1 i den k:e raden om Aₖ förekommer i paritetsekvationen för paritetsbiten Aⱼ och 0 annars.
• Raderna i denna matris är generatorerna i en kodgrupp med minsta avstånd på minst tre. Detta är den kod vi kommer att använda.

Som exempel kan vi anta att jag behöver en enkel kod med åtta ord och att jag bara behöver en grundläggande felupptäckt och inte korrigering, så jag kan komma undan med ett minsta avstånd på två. Jag vill ha tre informationsbitar och två paritetsbitar. Jag skriver ner följande paritetskontrollmatris:

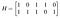
Det finns två kolumnpar som är lika, så det minsta t för vilket varje samling av t kolumner är linjärt oberoende är ett, så den minsta vikten, och därmed det minsta avståndet jag kommer att ha, är två. Raderna representerar paritetskontrollsekvationerna A₄=A₁+A₃ och A₅=A₁+A₂+A₃. Min genererande matris är därför:

Och raderna i denna matris genererar kodgruppen:

• {00000, 00111, 01001, 01110, 10011, 10100, 111010, 11101}

Slutanmärkningar

Abstrakt algebra är ett djupt ämne med långtgående implikationer, men det är också mycket lätt att lära sig. Bortsett från några få förbigående omnämnanden av linjär algebra är nästan allt som jag har diskuterat här tillgängligt för någon som bara har haft algebra på gymnasiet.

När jag först fick idén att skriva den här artikeln ville jag egentligen prata om Rubiks kub, men i slutändan ville jag välja ett exempel som kunde täckas endast med de mest grundläggande idéerna i gruppteori. Dessutom finns det så mycket att säga om Rubiks kubgrupp att den förtjänar en fristående artikel, så den kommer snart.

Mina högskolekurser i abstrakt algebra baserades på boken A Book of Abstract Algebra av Charles Pinter, som är och tillgänglig behandling. Exemplen i den här artikeln har alla lånats med vissa ändringar från Pinter.

Som en sista anmärkning, alla bilder som inte citeras är mina egna originalarbeten och får användas med angivande. Som alltid uppskattar jag eventuella korrigeringar eller önskemål om förtydliganden.