Eulers identitet verkar förbryllande:

Den kommer från en mer allmän formel:

Yowza – vi relaterar en imaginär exponent till sinus och cosinus! Och på något sätt ger pi -1? Kan detta någonsin vara intuitivt?

Inte enligt 1800-talets matematiker Benjamin Peirce:

Det är absolut paradoxalt; vi kan inte förstå det, och vi vet inte vad det betyder, men vi har bevisat det, och därför vet vi att det måste vara sanningen.

Argh, denna inställning får mitt blod att koka! Formler är inte magiska trollformler som man kan memorera: vi måste, måste, måste, måste hitta en insikt. Här är min:

Eulers formel beskriver två likvärdiga sätt att röra sig i en cirkel.

Så är det? Denna fantastiska ekvation handlar om att snurra runt? Ja – och vi kan förstå den genom att bygga på några analogier:

• Genom att börja med talet 1 kan du se multiplikation som en omvandling som förändrar talet: 1 $ \cdot e^{i \pi}$
• Reguljär exponentiell tillväxt ökar kontinuerligt 1 med en viss hastighet under en viss tidsperiod; imaginär exponentiell tillväxt roterar kontinuerligt 1 under en viss tidsperiod
• Att växa för ”pi” tidsenheter innebär att gå pi radianer runt en cirkel
• Därmed innebär $e^{i \pi}$ att man börjar vid 1 och roterar pi (halvvägs runt en cirkel) för att komma fram till -1

Det är en översikt på hög nivå, låt oss dyka ner i detaljerna. Förresten, om någon försöker imponera på dig med $e^{i \pi} = -1$, fråga dem om i till den i:e potensen. Om de inte kan tänka igenom det är Eulers formel fortfarande en trollformel för dem.

Uppdatering: Medan jag skrev tänkte jag att en video skulle kunna hjälpa till att förklara idéerna tydligare:

Understanding cos(x) + i * sin(x)

Det likhetstecknet är överbelastat. Ibland menar vi ”ställa en sak till en annan” (som x = 3) och ibland menar vi ”dessa två saker beskriver samma koncept” (som $\sqrt{-1} = i$).

Eulers formel är den senare: den ger två formler som förklarar hur man rör sig i en cirkel. Om vi undersöker cirkelrörelse med hjälp av trigonometri och färdas x radianer:

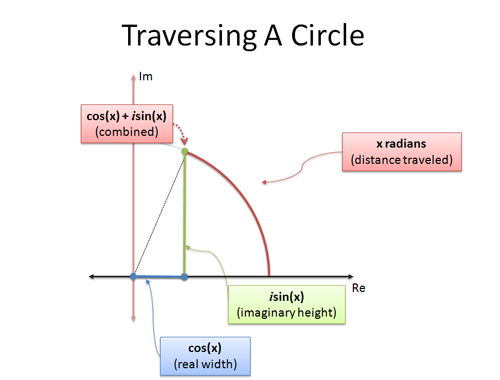
• cos(x) är x-koordinaten (horisontellt avstånd)
• sin(x) är y-koordinaten (vertikalt avstånd)

Satsen

är ett smart sätt att smälta x- och y-koordinaterna till ett enda tal. Analogin ”komplexa tal är tvådimensionella” hjälper oss att tolka ett enda komplext tal som en position på en cirkel.

När vi ställer x till $\pi$ reser vi $\pi$-enheter längs enhetscirkelns utsida. Eftersom den totala omkretsen är 2 $\pi$ är vanliga $\pi$ halvvägs runt, vilket gör att vi befinner oss vid -1.

Neo: Den högra sidan av Eulers formel ($\cos(x) + i \sin(x)$) beskriver cirkelrörelse med imaginära tal. Nu ska vi ta reda på hur e-sidan av ekvationen åstadkommer det.

Vad är imaginär tillväxt?

Att kombinera x- och y-koordinater till ett komplext tal är knepigt, men hanterbart. Men vad betyder en imaginär exponent?

Låt oss ta ett steg tillbaka lite. När jag ser $3^4$ tänker jag på det så här:

• 3 är slutresultatet av att växa omedelbart (med hjälp av e) med en hastighet av ln(3). Med andra ord: $3 = e^{\ln(3)}$
• $3^4$ är detsamma som att växa till 3, men sedan växa 4x så länge. Så $3^4 = e^{\ln(3) \cdot 4} = 81$

Istället för att se siffrorna i sig själva kan man se dem som något som e var tvungen att ”växa till”. Reella tal, som 3, ger en ränta på ln(3) = 1,1, och det är vad e ”samlar in” när det går framåt och växer kontinuerligt.

Reguljär tillväxt är enkel: den fortsätter att ”skjuta” ett tal i samma, reella riktning som det var på väg mot. 3 × 3 trycker på i den ursprungliga riktningen och gör det 3 gånger större (9).

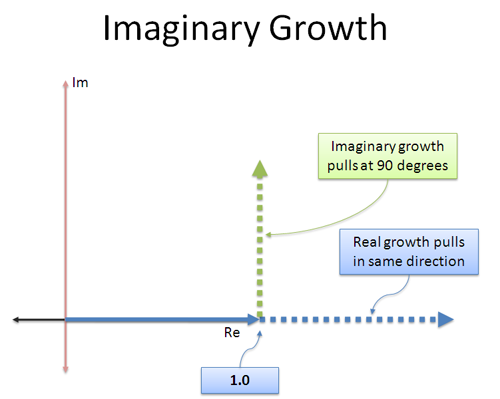
Den imaginära tillväxten är annorlunda: den ”ränta” vi tjänar in går i en annan riktning! Det är som en jetmotor som spänns fast i sidled – istället för att gå framåt börjar vi trycka på i 90 grader.

Det fina med en konstant ortogonal (vinkelrät) tryckning är att den inte gör dig snabbare eller långsammare – den roterar dig! Att ta ett tal och multiplicera det med i ändrar inte dess storlek, bara riktningen det pekar mot.

Intuitivt sett är det så här jag ser på kontinuerlig imaginär tillväxttakt: ”När jag växer, skjut mig inte framåt eller bakåt i den riktning jag redan går. Rotera mig istället.”

Men borde vi inte snurra snabbare och snabbare?

Jag undrade det också. Den vanliga tillväxten ökar i vår ursprungliga riktning, så vi går 1, 2, 4, 8, 16, multiplicerar 2x varje gång och stannar inom de verkliga talen. Vi kan betrakta detta som $e^{\ln(2)x}$, vilket innebär att vi växer omedelbart med en hastighet av ln(2) i ”x” sekunder.

Och hej – om vår tillväxthastighet var dubbelt så snabb, 2ln(2) jämfört med ln(2), skulle det se ut på samma sätt som att växa dubbelt så länge (2x jämfört med x). Magin i e gör att vi kan byta ut hastighet och tid; 2 sekunder med ln(2) är samma tillväxt som 1 sekund med 2ln(2).

Föreställ dig nu att vi har en rent imaginär tillväxthastighet (Ri) som roterar oss tills vi når i, eller 90 grader uppåt. Vad händer om vi fördubblar denna hastighet till 2Ri, kommer vi att snurra av cirkeln?

Nej! Att ha en hastighet på 2Ri innebär att vi bara snurrar dubbelt så fort, eller alternativt snurrar med en hastighet på R under dubbelt så lång tid, men vi stannar på cirkeln. Att rotera dubbelt så länge innebär att vi nu är vända 180 grader.

När vi väl inser att en viss exponentiell tillväxttakt kan ta oss från 1 till i så snurrar vi bara mer när vi ökar denna takt. Vi kommer aldrig att undkomma cirkeln.

Hursomhelst, om vår tillväxthastighet är komplex (a+bi vs Ri) så kommer den reella delen (a) att växa oss som vanligt, medan den imaginära delen (bi) roterar oss. Men låt oss inte bli för avancerade: Eulers formel, $e^{ix}$, handlar om den rent imaginära tillväxten som håller oss på cirkeln (mer senare).

En snabb sanitetskontroll

Under skrivandet var jag tvungen att klargöra några frågor för mig själv:

Varför använda $e^x$, roterar vi inte talet 1?

e representerar processen att börja vid 1 och växa kontinuerligt med 100 % ränta under 1 tidsenhet.

När vi skriver e fångar vi hela denna process i ett enda tal – e representerar hela den kontinuerliga tillväxtens rigorösa process. Så egentligen säger $e^x$ ”börja vid 1 och växa kontinuerligt med 100 % i x sekunder”, och börjar från 1 som vi vill.

Men vad gör i som exponent?

För en vanlig exponent som $3^4$ frågar vi oss:

• Vad är den implicita tillväxttakten? Vi växer från 1 till 3 (basen för exponenten).
• Hur ändrar vi tillväxttakten? Vi skalar den med 4x (exponentens potens).

Vi kan omvandla vår tillväxt till ”e”-format: vår momentana tillväxttakt är ln(3) och vi ökar den till ln(3) * 4. Återigen har exponentens potens (4) just skalat vår tillväxttakt.

När den översta exponenten är i (som i $3^i$), så multiplicerar vi bara vår implicita tillväxttakt med i. Så istället för att växa med vanlig ln(3) växer vi med ln(3) * i.

Den övre delen av exponenten ändrar den implicita tillväxthastigheten för den nedre delen.

Det viktiga detaljerna

Låta oss ta en närmare titt. Kom ihåg den här definitionen av e:

Det $\frac{100\%}{n}$ representerar den del ränta vi tjänat in under varje mikroskopisk period. Vi antog att räntan var 100 % i den reella dimensionen — men vad händer om den var 100 % i den imaginära riktningen?

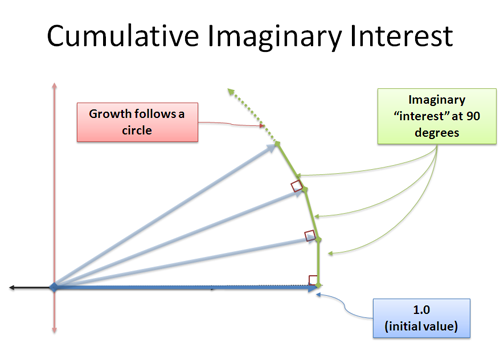
Nu lägger vår nybildade ränta till oss i 90-graders riktning. Överraskande nog ändrar detta inte vår längd — detta är ett knepigt begrepp, eftersom det ser ut att skapa en triangel där hypotenusan måste vara större. Vi har att göra med en gräns, och det extra avståndet ligger inom den felmarginal vi anger. Detta är något jag vill ta itu med en annan dag, men ta mitt ord: kontinuerlig vinkelrät tillväxt kommer att rotera dig. Detta är hjärtat av sinus och cosinus, där din förändring är vinkelrät mot din nuvarande position och du rör dig i en cirkel.

Vi tillämpar i enheter av tillväxt i oändligt små steg, var och en skjuter oss i en 90-graders vinkel. Det finns ingen ”snabbare och snabbare” rotation – istället kryper vi längs omkretsen en sträcka på |i| = 1 (storleken på i).

Och hej – sträckan man kryper runt en cirkel är en vinkel i radianer! Vi har hittat ett annat sätt att beskriva cirkelrörelse!

För att få cirkelrörelse: För att få en cirkelrörelse: ändra kontinuerligt genom att rotera i en 90-graders vinkel (aka imaginär tillväxttakt).

Eulers formel säger alltså att ”exponentiell, imaginär tillväxt spårar ut en cirkel”. Och denna bana är densamma som att röra sig i en cirkel med hjälp av sinus och cosinus i det imaginära planet.

I det här fallet är ordet ”exponentiell” förvirrande eftersom vi rör oss runt cirkeln med en konstant hastighet. I de flesta diskussioner antas exponentiell tillväxt ha en kumulativ, sammansatt effekt.

Några exempel

Du tror mig inte riktigt, eller hur? Här är några exempel och hur man intuitivt kan tänka på dem.

Exempel: $e^i$

Var är x? Ah, det är bara 1. Intuitivt, utan att ta fram en miniräknare, vet vi att detta betyder ”resa 1 radian längs enhetscirkeln”. I mitt huvud ser jag hur ”e” försöker växa 1 på 100 % i samma riktning, men i fortsätter att flytta bollen och tvingar ”1” att växa längs cirkelns kant:

Inte det vackraste talet, men där är det. Kom ihåg att sätta din miniräknare i radianläge när du slår in detta.

Exempel: $3^i$

Det här är knepigt – det är inte i vårt standardformat. Men kom ihåg att

Vi vill ha en initial tillväxt på 3x i slutet av perioden, eller en momentan hastighet på ln(3). Men, i:et kommer och ändrar denna hastighet av ln(3) till ”i * ln(3)”:

Vi trodde att vi skulle transformera med en vanlig hastighet av ln(3), lite snabbare än 100 % kontinuerlig tillväxt eftersom e är ungefär 2,718. Men åh nej, jag snurrade runt oss: nu transformeras vi med en imaginär hastighet vilket innebär att vi bara roterar runt. Om i var ett regelbundet tal som 4 skulle det ha fått oss att växa 4x snabbare. Nu växer vi med en hastighet av ln(3), men i sidled.

Vi borde förvänta oss ett komplext tal på enhetscirkeln – det finns inget i tillväxthastigheten som ökar vår storlek. Lösa ekvationen:

Så istället för att hamna ”1” enhet runt cirkeln (som $e^i$) hamnar vi ln(3) enheter runt.

Exempel: $i^i$

För några månader sedan skulle detta ha fått mig att gråta. Inte i dag! Låt oss dela upp transformationerna:

Vi börjar med 1 och vill ändra det. Som att lösa $3^i$, vad är den momentana tillväxttakten som representeras av i som bas?

Hrm. Normalt skulle vi göra ln(x) för att få fram den tillväxttakt som krävs för att nå x i slutet av 1 tidsenhet. Men för en imaginär tillväxttakt? Vi måste nudla om detta.

För att börja med 1 och växa till i måste vi börja rotera från början. Hur snabbt? Jo, vi måste få 90 grader (pi/2 radianer) på 1 tidsenhet. Så vår hastighet är $i \frac{\pi}{2}$. Kom ihåg att vår hastighet måste vara imaginär eftersom vi roterar, inte växer! Vanliga $\frac{\pi}{2}$ är ungefär 1,57 och resulterar i regelbunden tillväxt.

Detta borde vara logiskt: för att vända 1,0 till i i slutet av 1 enhet ska vi rotera $\frac{\pi}{2}$ radianer (90 grader) på den mängden tid. Så för att få ”i” kan vi använda $e^{i \frac{\pi}{2}}$.

Phew. Det beskriver i som bas. Hur är det med exponenten?

Ja, det andra i talar om för oss att ändra vår hastighet – ja, den där hastigheten som vi ägnade så lång tid åt att räkna ut! Så i stället för att rotera med en hastighet av $i \frac{\pi}{2}$, vilket är vad en bas av i innebär, omvandlar vi hastigheten till:

I:na upphäver varandra och gör tillväxttakten verklig igen! Vi roterade vår ränta och tryckte oss in i de negativa siffrorna. Och en negativ tillväxttakt innebär att vi krymper – vi bör förvänta oss att $i^i$ gör saker och ting mindre. Och det gör det:

Tada! (Sök ”i^i” på Google för att använda dess kalkylator)

Ta en paus: Du kan intuitivt räkna ut hur imaginära baser och imaginära exponenter ska bete sig. Whoa.

Och som en bonus har du räknat ut ln(i) – för att få $e^x$ att bli i, får du e att rotera $\frac{\pi}{2}$ radianer.

Exempel: (i^i)^i

En dubbel imaginär exponent? Om du insisterar. För det första vet vi vad vår tillväxthastighet kommer att vara innanför parentesen:

Vi får en negativ (krympande) tillväxthastighet på -pi/2. Och nu modifierar vi den hastigheten igen med i:

Och nu har vi en negativ rotation! Vi går runt cirkeln med en hastighet av $-\frac{\pi}{2}$ per tidsenhet. Hur länge går vi? Tja, det finns en implicit ”1” tidsenhet längst upp i denna exponentkedja; den implicita standardinställningen är att gå för 1 tidsenhet (precis som $e = e^1$). 1 tidsenhet ger oss en rotation på $-\frac{\pi}{2}$ radianer (-90 grader) eller -i!

Och, bara för skojs skull, om vi kvadrerar detta galna resultat:

Det är ”bara” en dubbelt så stor rotation: 2 är ett regelbundet tal så det fördubblar vår rotationshastighet till hela -180 grader på en tidsenhet. Eller så kan man se det som att man tillämpar -90 graders rotation två gånger i rad.

I förstone är detta verkligen märkliga exponenter. Men med våra analogier kan vi ta dem med ro.

Komplex tillväxt

Vi kan ha reell och imaginär tillväxt samtidigt: den reella delen skalar upp oss, och den imaginära delen roterar oss runt:

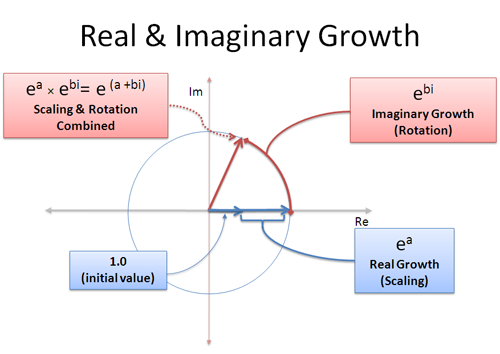
En komplex tillväxt som (a + bi) är en blandning av reell och imaginär tillväxt. Den verkliga delen a betyder ”växa med 100 % i a sekunder” och den imaginära delen b betyder ”rotera i b sekunder”. Kom ihåg att rotationer inte får fördelen av sammansättning eftersom du fortsätter att ”trycka” i en annan riktning – rotation adderas linjärt.

Med detta i åtanke kan vi representera vilken punkt som helst på en cirkel av vilken storlek som helst med hjälp av (a+bi)! Radien är $e^a$ och vinkeln bestäms av $e^{bi}$. Det är som att sätta numret i expand-o-tron i två cykler: en gång för att växa det till rätt storlek (a sekunder), en annan gång för att rotera det till rätt vinkel (b sekunder). Eller så kan man rotera det först och sedan växa!

Vad sägs om att vi vill veta tillväxtmängden för att komma till 6 + 8i. Detta är egentligen en fråga om den naturliga loggen av ett imaginärt tal: hur växer vi e för att få (6 + 8i)?

• Radius: Hur stor cirkel behöver vi? Tja, storleken är $\sqrt{6^2 + 8^2} = \sqrt{100} = 10$. Det betyder att vi måste växa i ln(10) = 2,3 sekunder för att nå det beloppet.
• Mängden att rotera: Vad är vinkeln på den punkten? Vi kan använda arctan för att räkna ut det: atan(8/6) = 53 grader = 0,93 radian.
• Kombinera resultatet: ln(6+8i) = 2,3 + 0,93i

Det innebär att vi kan nå den slumpmässiga punkten (6 + 8i) om vi använder $e^{2.3 + .93i}$.

Varför är detta användbart?

Eulers formel ger oss ett annat sätt att beskriva rörelse i en cirkel. Men vi kan redan göra det med sinus och cosinus – vad är det som är så speciellt?

Det handlar om perspektiv. Sinus och cosinus beskriver rörelsen i termer av ett rutnät, där horisontella och vertikala koordinater ritas ut.

Eulers formel använder polära koordinater — vad är din vinkel och ditt avstånd? Återigen är det två sätt att beskriva rörelse:

• Grid-system: Gå 3 enheter österut och 4 enheter norrut
• Polära koordinater: Beroende på problemet är polära eller rektangulära koordinater mer användbara. Med Eulers formel kan vi konvertera mellan de två för att använda det bästa verktyget för uppgiften. Eftersom $e^{ix}$ kan omvandlas till sinus och cosinus kan vi också skriva om formler i trigonometri som variationer på e, vilket är mycket praktiskt (du behöver inte memorera sin(a+b), du kan härleda det – mer en annan dag). Och det är vackert att varje tal, verkligt eller komplext, är en variation av e.

  Men nytta, schmutility: det viktigaste resultatet är insikten att förbryllande ekvationer kan bli intuitiva med rätt analogier. Låt inte vackra ekvationer som Eulers formel förbli en trollformel – bygg på de analogier du känner till för att se insikterna inuti ekvationen.

  Happy math.

  Appendix

  Screentcasten var rolig, och feedback är definitivt välkommen. Jag tror att det hjälper idéerna att komma fram, och att gå igenom artikeln hjälpte mig att hitta luckor i min intuition.

  • Brian Slesinsky har en snygg presentation om Eulers formel
  • Visual Complex Analysis har en bra diskussion om Eulers formel – se s. 10 i Google Book Preview
  • Jag höll en föreläsning om Math and Analogies som förklarar Eulers identitet mer visuellt:

  

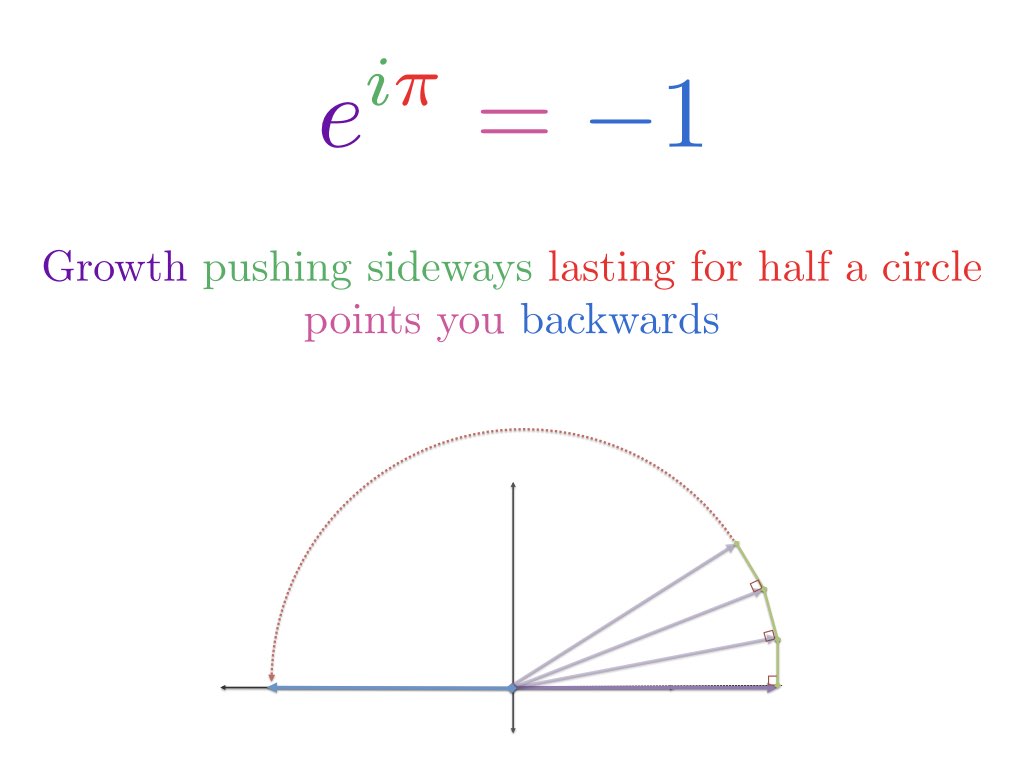
  Andra inlägg i denna serie

  1. En visuell, intuitiv guide till imaginära tal
  2. Intuitiv aritmetik med komplexa tal
  3. Förstå varför komplexa multiplikationer fungerar
  4. Intuitiv guide till vinklar, Grader och radianer
  5. Intuitiv förståelse av Eulers formel
  6. Interaktiv guide till Fouriertransformationen
  7. Intuitiv guide till konvolution
  9. Intuitiv förståelse av sinusvågor
  10. En intuitiv guide till linjär algebra
  11. En programmerares intuition för matrismultiplikation
  12. Imaginär multiplikation vs. Imaginära exponenter