En asymptot är en linje som en graf närmar sig men inte skär.
I den här lektionen lär vi oss hur man hittar vertikala asymptoter, horisontella asymptoter och sneda (sneda) asymptoter för rationella funktioner.
Relaterade ämnen:
Flera lektioner om kalkyl

Det följande diagrammet visar de olika typerna av asymptoter: horisontella asymptoter, vertikala asymptoter och sneda asymptoter. Scrolla nedåt på sidan för fler exempel och lösningar på hur man hittar asymptoter.

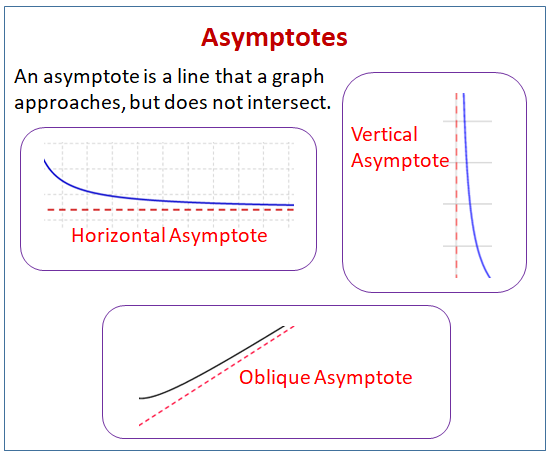
Hur man bestämmer den vertikala asymptoten?

Metod 1: Använd definitionen av vertikal asymptot

Linjen x = a kallas för en vertikal asymptot till kurvan y = f(x) om minst ett av följande påståenden är sant.

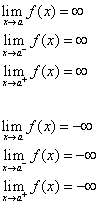
Metod 2:

För rationella funktioner är vertikala asymptoter vertikala linjer som motsvarar nollpunkterna i nämnaren.
Giv den rationella funktionen f(x)

Steg 1: Skriv f(x) i reducerad form

Steg 2: Om x – c är en faktor i nämnaren så är x = c den vertikala asymptoten.

Exempel:

Finn de vertikala asymptotorna till

Lösning:

Metod 1: Använd definitionen av vertikal asymptot.

Om x är nära 3 men större än 3 är nämnaren x – 3 ett litet positivt tal och 2x är nära 8. Så är ett stort positivt tal.

Intuitivt ser vi att

Samma sak gäller om x är nära 3 men mindre än 3, då är x – 3 ett litet negativt tal och 2x är nära 8. Så är ett stort negativt tal.

Linjen x = 3 är den vertikala asymptoten.

Metod 2:

Steg 1: f(x) är redan i reducerad form.

Steg 2: Nämnaren är x – 3, så den vertikala asymptoten ligger vid x = 3.

Finnande av vertikala asymptoter för rationella funktioner

Vad man ska leta efter för att hitta vertikala asymptoter för rationella funktioner.

• Visa steg-för-steg-lösningar

Vertikala asymptoter för rationella funktioner: Snabbt sätt att hitta dem

Exempel på hur man hittar vertikala asymptoter för rationella funktioner.

• Visa steg-för-steg-lösningar

Hur man hittar vertikala asymptoter för rationella funktioner

• Visa steg-för-steg-lösningar

Hur man bestämmer den horisontella asymptoten?

Metod 1: Använd definitionen av horisontell asymptot

Linjen y = L kallas horisontell asymptot till kurvan y = f(x) om antingen

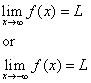
Metod 2:

För den rationella funktionen f(x)

Om graden x i täljaren är mindre än graden x i nämnaren så är y = 0 den horisontella asymptoten.

Om graden av x i täljaren är lika med graden av x i nämnaren så är y = c där c fås genom att dividera de ledande koefficienterna.

Exempel:

Hitta funktionens horisontella och vertikala asymptoter.

Lösning:

Metod 1:

Divider både täljare och nämnare med x.

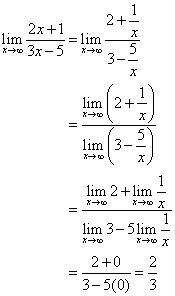
Linjen är den horisontella asymptoten.

Metod 2:

Graden x i täljaren är lika med graden x i nämnaren.

Dividerar vi de ledande koefficienterna får vi

Linjen är den horisontella asymptoten.

Skutt för att hitta horisontella asymptoter för rationella funktioner

Ett par knep som gör det väldigt enkelt att hitta horisontella asymptoter för rationella funktioner

• Visa steg-för-steg-lösningar

Den här videon kommer att ge en grundläggande översikt över horisontella asymptoter. Vi kommer att avgöra om de givna rationella funktionerna har horisontella asymptoter och vad de är.

• Visa steg-för-steg-lösningar

Den här videon kommer att gå in mer i detalj på regler för horisontella asymptoter.

• Visa steg-för-steg-lösningar

Oblig asymptot eller sned asymptot

En del kurvor har asymptoter som är sneda, dvs. varken horisontella eller vertikala.

Om så kallas linjen y = mx + b för sned asymptot eller sned asymptot eftersom de vertikala avstånden mellan kurvan y = f(x) och linjen y = mx + b närmar sig 0.

För rationella funktioner uppträder sned asymptot när täljarens grad är en mer än nämnarens grad. I ett sådant fall kan ekvationen för den sneda asymptoten hittas genom lång division.

Exempel:

Finn asymptoterna för funktionen

Lösning: Det är en enkel formel för att hitta asymptoterna för funktionen

:

Då nämnaren x2 + 1 aldrig är 0 finns det ingen vertikal asymptot.

Då graden x i täljaren är större än graden x i nämnaren finns det ingen horisontell asymptot.

Då graden x i täljaren är en gång större än graden x i nämnaren kan vi med hjälp av lång division få fram den sneda asymptoten.

Så linjen y = x är den sneda asymptoten.

Finnande av sneda asymptoter för rationella funktioner

Denna video beskriver när en rationell funktion har en sned asymptot, beskriver kortfattat vad en sned asymptot är och ger sedan två exempel.

• Visa steg-för-steg-lösningar

Hitta asymptoter av en rationell funktion (vertikal, horisontell och sned/skrå)

Denna video visar hur man hittar de vertikala asymptoterna och en sned/skrå asymptoter av en rationell funktion.

• Visa steg-för-steg-lösningar

Finnande av alla asymptoter av en rationell funktion (vertikal, horisontell, sned/skrå)

Här tittar vi på en funktion och hittar den vertikala asymptoten och drar också slutsatsen att det inte finns några horisontella asymptoter, men att en sned asymptot finns. Vi använder sedan lång division för att hitta den sneda asymptoten.

• Visa steg-för-steg-lösningar

Prova den kostnadsfria Mathway-kalkylatorn och problemlösaren nedan för att öva olika matematiska ämnen. Prova de givna exemplen eller skriv in ditt eget problem och kontrollera ditt svar med hjälp av de stegvisa förklaringarna.