Professor Fishers noter om dette emne i PDF
Professor Fishers lysbilleder om dette emne i PDF (password påkrævet)
Gamle lysbilleder fra professor Sekula i PDF.

Induktion

Note: Filosoffer (herunder professor Sekula, professor Sekula og professor M. Fisher) skelner mellem induktion (generalisering af træk ved nogle prøver til andre ting) og abduktion (slutning til den bedste forklaring), hvorimod indholdet nedenfor blander begge dele sammen under den fælles overskrift “induktion”. Når du tager dette kursus med professor Fisher, er det bedre at stole på hans noter eller dias om dette emne end på nedenstående indhold.

Induktion er en proces, hvor man forsøger at finde ud af, hvordan et fænomen fungerer ved at studere en prøve af det. Man arbejder med en prøve, fordi det ikke er muligt at undersøge alle komponenter af fænomenet.Induktion er en kreativ proces. Forskeren skal omhyggeligt studere en prøve af et fænomen og derefter formulere en hypotese, der kan forklare fænomenet.Herefter følger den videnskabelige proces med afprøvning af hypotesen.Videnskabsmænd, der opnår de mest spektakulære forskningsresultater, er dem, der er kreative nok til at finde på de rigtige forskningsspørgsmål.

Naturvidenskab (fysik, kemi, biologi osv.) er induktiv.Man indsamler beviser. Den videnskabelige metode anvendes.Start med specifikke resultater (en prøve) og prøv at gætte på de generelle regler. Hypoteser kan kun modbevises, aldrig bevises. Hvis en hypotese kan modstå gentagne forsøg foretaget af mange uafhængige forskere, vokser tilliden til hypotesen. Alle hypoteser er foreløbige; enhver hypotese kan blive omstødt i morgen, men der kræves meget stærke beviser for at omstøde en “lov” eller “kendsgerning”.

Specifik -> Generel

Her er et eksempel på induktion: Lad os antage, at jeg har taget 20 kugler tilfældigt fra en stor pose med kugler. Hver eneste af dem viste sig at være hvide. Det er minobservation – hver eneste kugle jeg tog ud var hvid. Jeg kunne derfor opstille den hypotese, at dette ville kunne forklares, hvis alle kuglerne i posen var hvide. Det kan være, at der er nogle forskelligfarvede kugler i posen, og at min første prøve simpelthen ikke ramte nogen.

Det er tilfældigvis et tilfælde, hvor vi kan bevise, at hypotesen er sand.Vi kan simpelthen smide alle kuglerne i posen ud og undersøge hver enkelt.En sådan procedure kaldes en optælling – se på hver enkelt kugle. I de fleste tilfælde, hvor induktion anvendes, er det ikke muligt at foretage en optælling.

Abduktion: Dette er en ræsonnementmetode, der ikke er stringent som deduktion.Antag, at du har observationer af en interessant hændelse. Du er ikke umiddelbart sikker på, hvad der forklarer observationerne. Du tænker på alle de hypoteser du kan, som kunne forklare observationerne på en plausibel måde.Dette er en kreativ proces i modsætning til deduktion. Du er nødt til at vide så meget som muligt om situationen, for at det kan fungere godt. I betragtning af alt det, du ved, vælger du den hypotese, der virker mest rimelig og sandsynlig. du har valgt den tilsyneladende bedste forklaring, selv om den kan være forkert. der er ingen garanti. Yderligere kontrol af din forklaring er normalt en god idé, hvis det er muligt; du kan finde flere oplysninger, som kan få dig til at genoverveje din konklusion.

Denne slags ræsonnementer er Sherlock Holmes’ stærke side. Conan Doyles berygtede hyperopmærksomme detektiv opdager selv meget små spor, som politiinspektøren normalt overser. Holmes kombinerer disse spor med den generelle viden, han har opbygget om sagen, for at komme frem til den bedste forklaring – whodunit! Han forklarer også, hvordan forbrydelsen blev begået.Som en fin detalje for læseren forklarer Holmes ofte de ræsonnementer, der førte ham frem til løsningen. Det virker simpelt, når Holmes forklarer det…

Deduktion

Matematik er en deduktiv videnskab. Der foreslås aksiomer. De bliver ikke testet; de antages at være sande. Sætninger udledes af aksiomerne. Givet aksiomerne og de logiske regler kan en maskine producere sætninger.

Generelt -> Specifikt

Start med den generelle regel og udled specifikke resultater.Hvis sætningen af aksiomer producerer en sætning og dens negation, kaldes sætningen af aksiomer INCONSISTENT.

Sæt, at vi har følgende kendte forhold.

• Vi har en stor pose med kugler.
• Alle kugler i posen vides at være hvide.
• Jeg har en tilfældig prøve på 20 kugler taget fra posen.

Deraf kan jeg udlede, at alle kugler i prøven er hvide, selv uden at jeg ser på dem. Denne form for ræsonnement kaldes modus ponens (mere om dette nedenfor og i professor Fishers noter).

Hvad med dette?

• Vi har en stor pose med kugler.
• Alle kugler i posen er hvide.
• Jeg har en prøve på 20 kugler af blandede farver.

Deraf kan jeg hurtigt udlede, at prøven ikke blev taget fra posen med hvide kugler. Denne form for ræsonnement kaldes modus tollens (mere herom nedenfor og i professor Fishers noter).

Deduktive argumenter

Lad os se på ideen om deduktive ræsonnementer (udledt fra professor Fishers noter).Her er der tale om at argumentere for en idé eller en konklusion på grundlag af et sæt præmisser (fakta, idéer osv.) Prof. Fisher bemærker, at filosoffer normalt viser dette som

1. Premise number 12. Premise number 2...------------------------C. Conclusion to be reached

Denne struktur udgør et argument.Den bliver nogle gange skrevet som
Præmis 1, Præmis 2, Præmis… => Konklusion.
Lad os forkortere dette til syllogismen på denne måde:
P => C (Præmisser indebærer Konklusion, ligesom ovenfor)
Dette betyder simpelthen, at hvis præmisserne er sande, så er konklusionen også sand.
“For at være god skal et argument have sande præmisser, og præmisserne skal give støtte for konklusionen. Den stærkest mulige støtte ville give en absolut garanti for, at konklusionen er sand (naturligvis under forudsætning af, at præmisserne er sande).Vi vil først se på denne form for støtte, men derefter vil vi også se på nogle svagere former for støtte.” (fra professor Fisher)

En særlig nyttig form for argument er et deduktivt gyldigt argument. (Dette forkortes ofte som “gyldigt argument” eller nogle gange som “deduktivt argument”.)Deduktivt gyldige argumenter er argumenter, hvor præmisserne, hvis de var sande, ville være det stærkest mulige bevis for, at konklusionen er sand. Disse argumenter giver nemlig følgende garanti: Hvis præmisserne er sande, må konklusionen også være sand.
Et argument, der tilsyneladende er deduktivt, men som har præmisser, der ikke understøtter konklusionen (ingen garanti), er et ugyldigt argument.
Lad os gentage syllogismen P => C (præmisser fører til konklusion).Der er fire mulige påstande, som du kan fremsætte om dette:

1. Alle præmisserne er sande (P er sandt) (modus ponens-argumentation)
2. En eller flere af præmisserne er falske (P er falsk – ikke P)
3. Konklusionen er sand (C er sand)
4. Konklusionen er falsk (C er falsk – ikke C) (modus tollens-argumentation)

Kun to af disse (nr. 1 og 4) udgør deduktivt gyldige ræsonnementer.Lad os se på årsagen til dette, et valg ad gangen.

1. P er sandt (P) – Bekræftelse af antecedent. Hvis alle præmisserne er sande, må konklusionen være sand. Dette er et meget stærkt argument. (modus ponens)
3. P er falsk (ikke P) – Benægtelse af antecedenten. At P er falsk garanterer ikke, at C er enten sand eller falsk. Der kan være andre årsager.
4. C er sandt (C) – Bekræftelse af konsekvenserne. Hvis C er sandt, kan det være af en af flere årsager, ikke af denne specifikke P.
6. C er falsk (ikke C) – Benægtelse af konsekvensen. Her må P også være falsk, hvis C er falsk. Hvis P var sandt, ville C også være det. (modus tollens)

Kort sagt er #1 og #4 (modus ponens og modus tollens) deduktivt gyldige, mens #2 og #3 ikke er det.
Hvis præmisserne gælder for ting i den virkelige verden, skal du stadig lave en test for ugyldighed. Der er mindst tre fremgangsmåder.

1. Se, om du kan finde et scenarie, hvor præmisserne er sande, men konklusionen er falsk.
2. Forsøg at erstatte et substantiv eller adjektiv i argumentet med et andet.
3. Forsøg at erstatte alle forekomster. Hvis dette tydeligvis ikke er gyldigt, er det oprindelige argument ikke gyldigt.
4. Repræsentér P og C i et Venn-diagram.Hvis du kan gøre det således, at P er sandt, men C er falsk, er argumentet ugyldigt. Vi har lavet disse diagrammer til dig nedenfor.

Nu tager vi emnet Venn-diagrammer op. Disse kan være af stor værdii forbindelse med kontrol af præmisserne i et argument.

Venn-diagrammer

Venn-diagrammer er en grafisk metode til at repræsentere logik.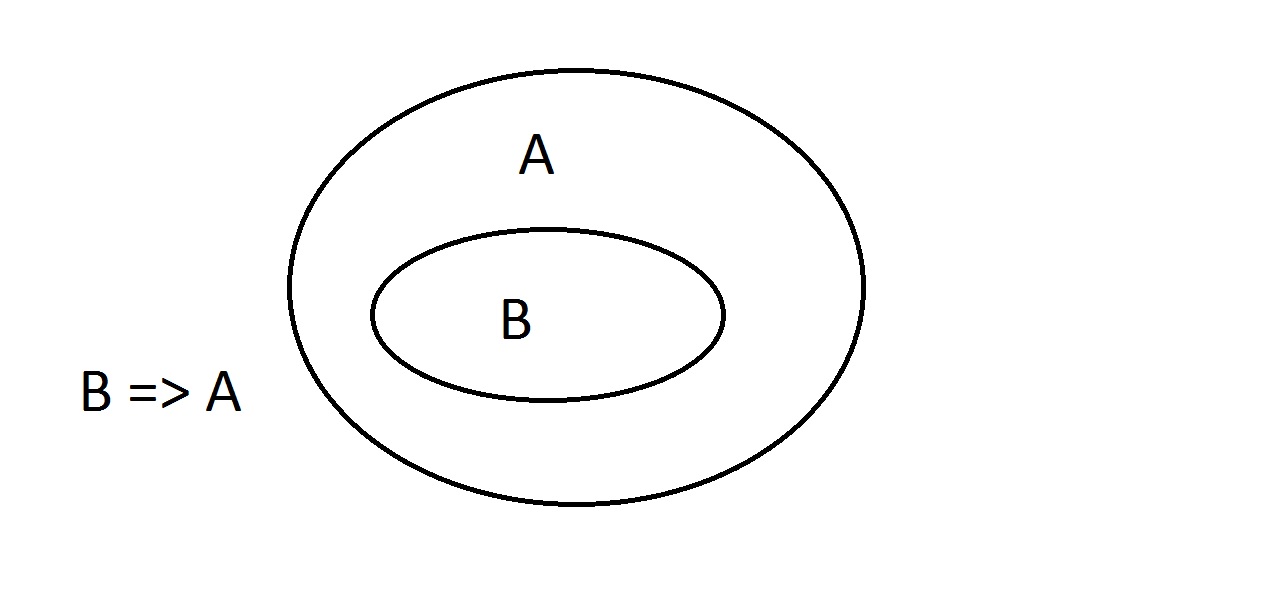
Dette er omtrent det enkleste diagram, du vil få. Den ydre oval indeholder alle ting, der har egenskaben A, mens den indre oval indeholder alle ting, der har egenskaben B samt egenskaben A. Dette er vist som B=>A, hvilket betyder, at alle ting, der har egenskaben B, også har egenskaben A. Man kan også sige “B indebærer A.” Hvis B er sandt, så må A også være det. Dette er den garanti, der er nævnt ovenfor.
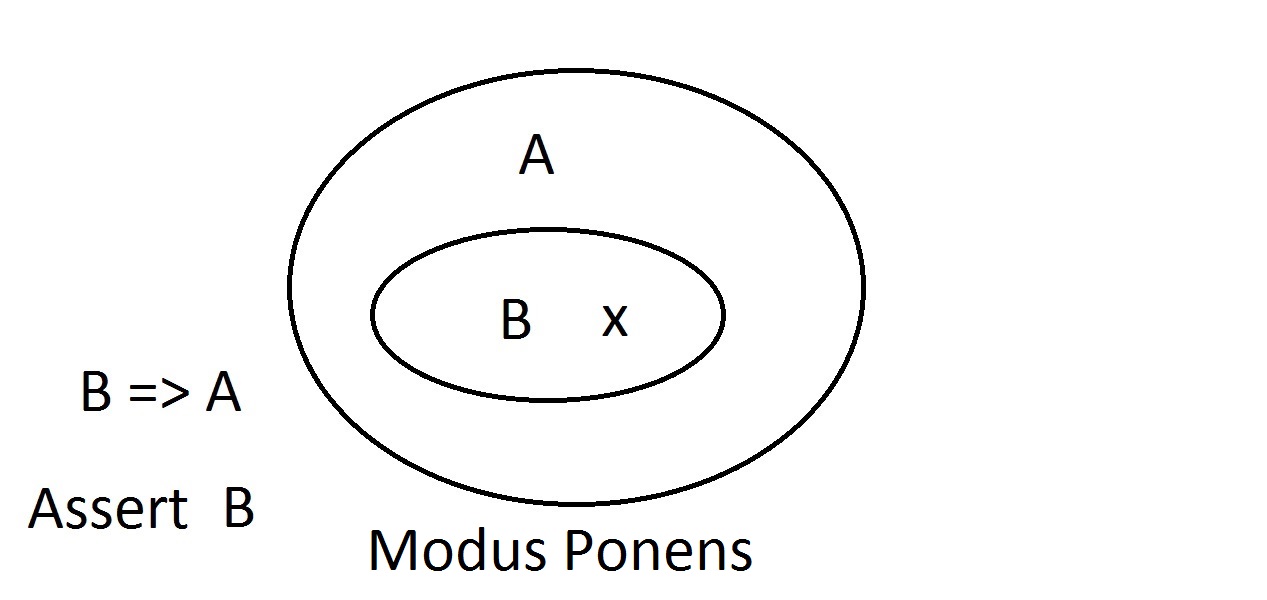Vi vil nu hævde, at vi har noget med egenskaben B. Vi kan med sikkerhed hævde, at ithar egenskaben A også. Dette er Modus Ponens-argumentation (bekræftelse af antecedent). Enhver enhed med egenskab B må naturligvis også være i rummet med egenskab A.
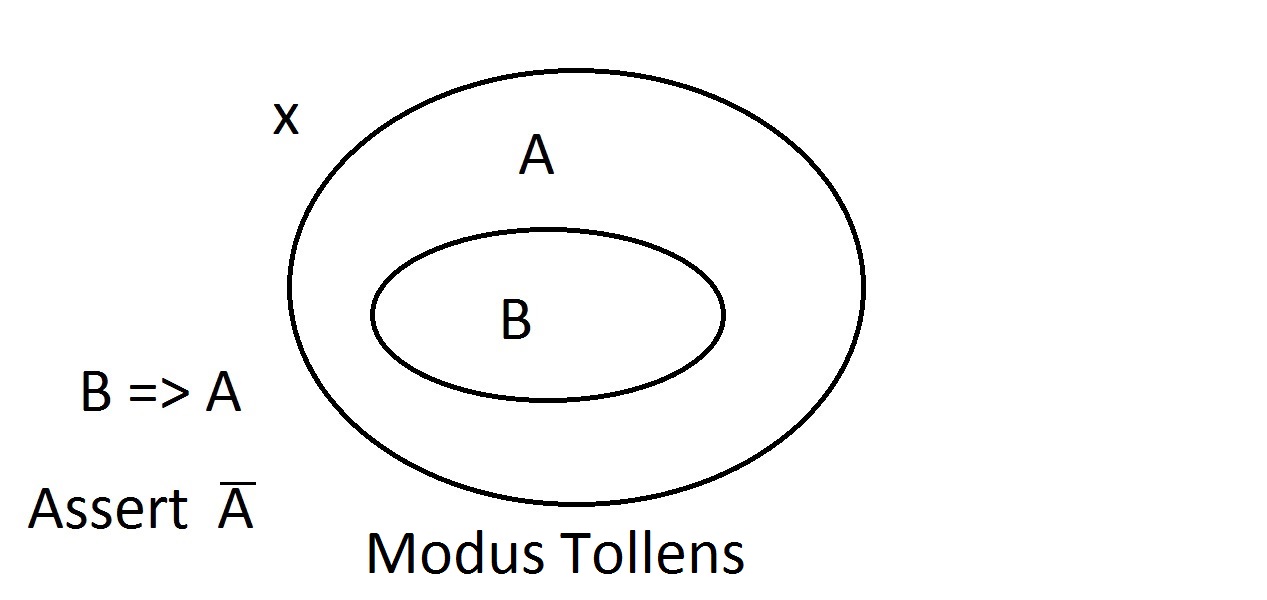Sæt nu, at vi hævder, at en enhed ikke har egenskab A. Venn-diagrammet viser, at den heller ikke kan have egenskab B. Alt, der ligger uden for egenskab A, må også ligge uden for egenskab B. Dette er Modus Tollens-argumentation (benægtelse af det konsekutive) og er gyldig og stærk.
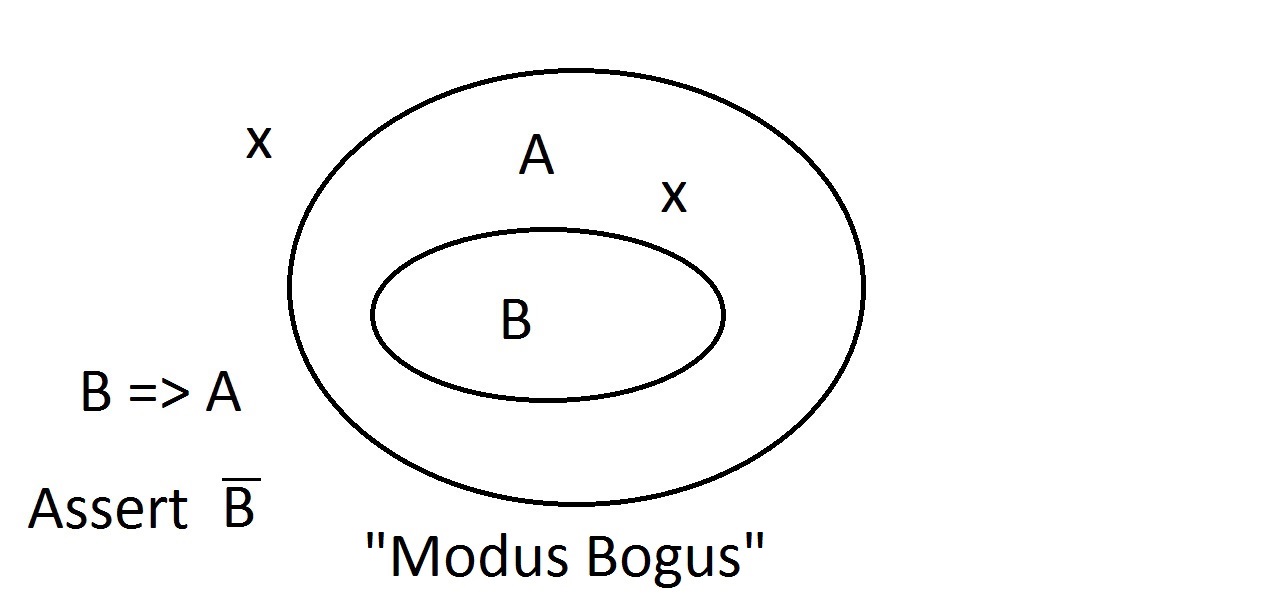Nu vil vi prøve at hævde, at vores ting ikke besidder egenskab B. Et kig på Venn-diagrammet viser problemet her. En enhed, der ikke har egenskab B, kan ligge inden for A-rummet eller uden for det. Påstanden om “ikke B” fortæller os intet om A. Dette er ikke et gyldigt ræsonnement, så vi kaldte det Modus Bogus. Det er at benægte antecedenten og er ikke gyldigt.
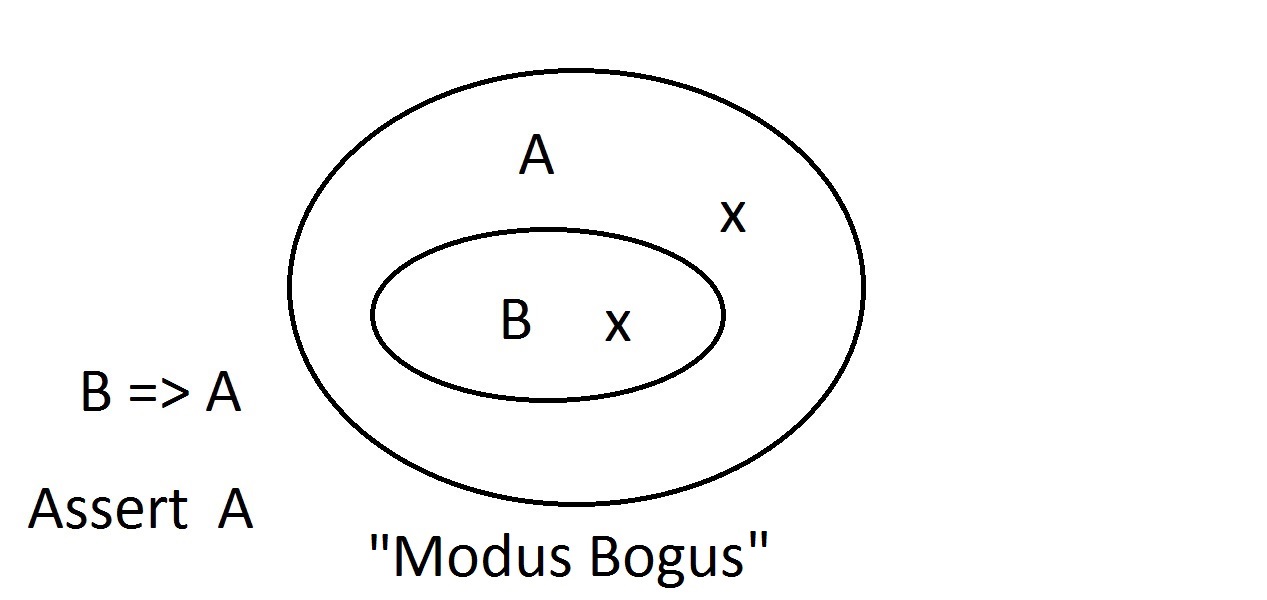Den sidste mulighed er at hævde, at vores ting har egenskab A. Venn-diagrammet viser problemet. Enheden kunne ligge hvor som helst i A-rummet,enten inden for eller uden for B-rummet. At hævde, at tingen har egenskaben A fortæller dig intet om, hvorvidt den også har B. Dette er også Modus Bogus, eller ugyldig ræsonnement. det kaldes at bekræfte konsekvensen.
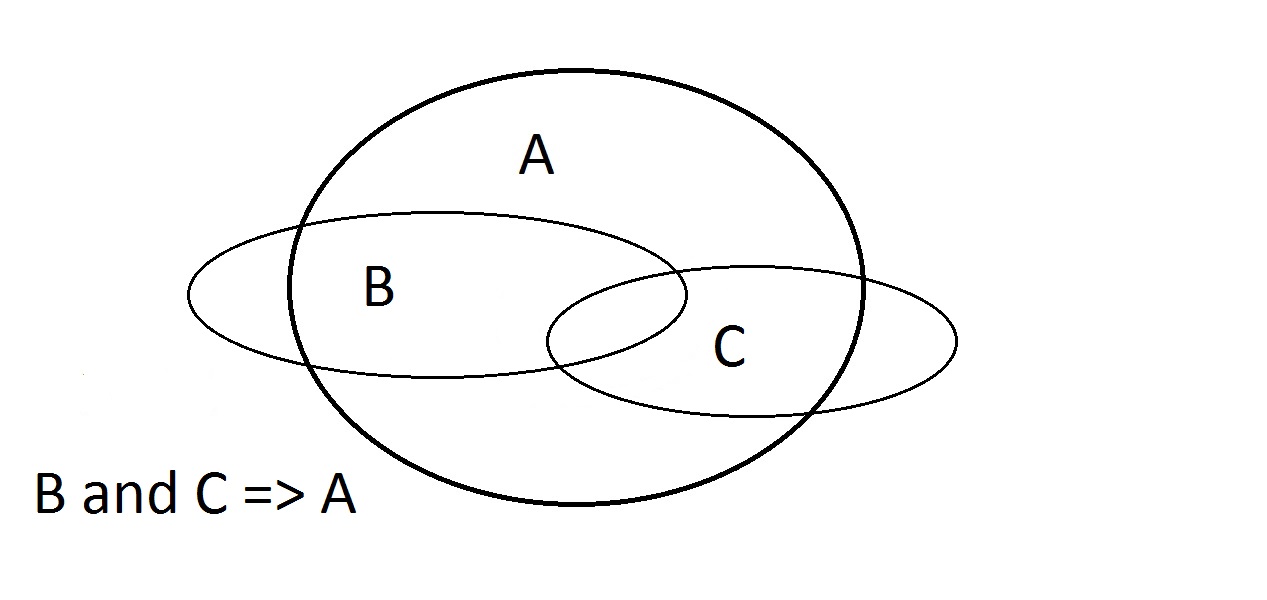Her har vi at gøre med egenskaberne A, B og C. Her kan vi kun garantere, at en enhed, der har B og C, også har A. Bemærk, at nogle af B- og C-rummene ligger uden for A.

• Vurder A: Kunne være hvor som helst i A
• Vurder B: Noget af B ligger uden for A
• Vurder C: Noget af C ligger uden for A
• Vurder A og B: Kunne omfatte noget C; måske ikke.
• Sværg B og C: Skæringspunktet BC ligger helt i A. At argumentere for, at B og C => A virker.
• Sværg A og C: Kan omfatte noget B; måske ikke

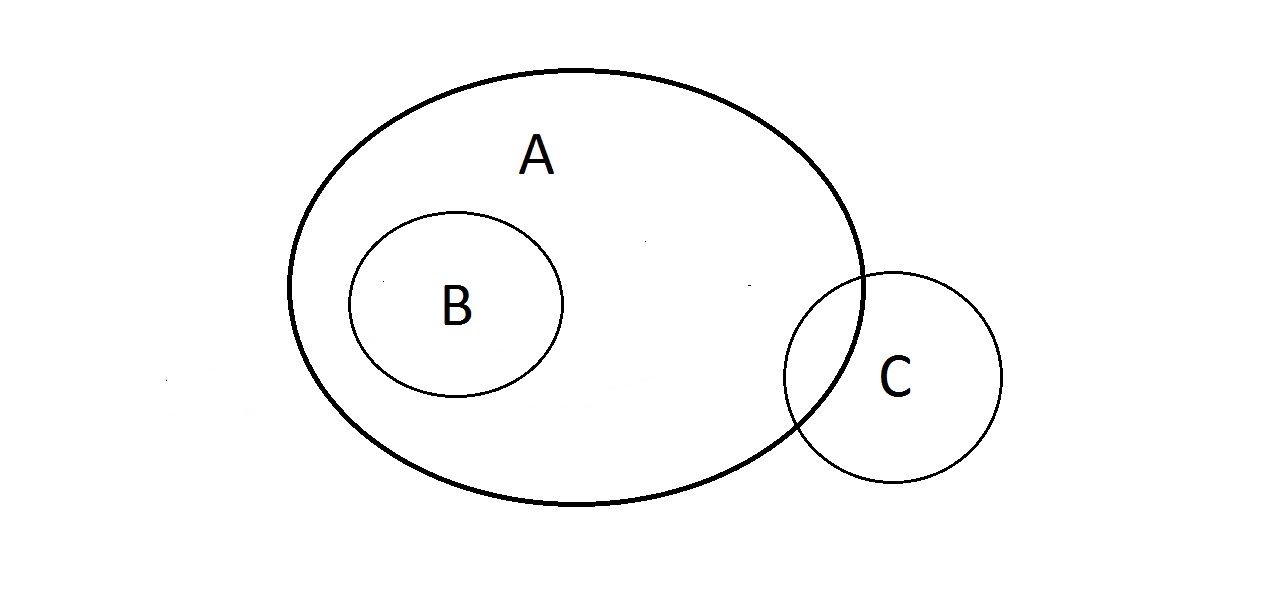
Hvad kan du gøre med dette? Egenskaberne A og B er som ovenfor, men hvad med C? Noget, der har egenskaben C, kan ligge inden for A, eller også kan det ikke. Noget i A kan også ligge i C, eller også kan det ikke. Du kan ikke gøre noget med C her. Vi har dog en garanti for, at noget, der har B, også har A.

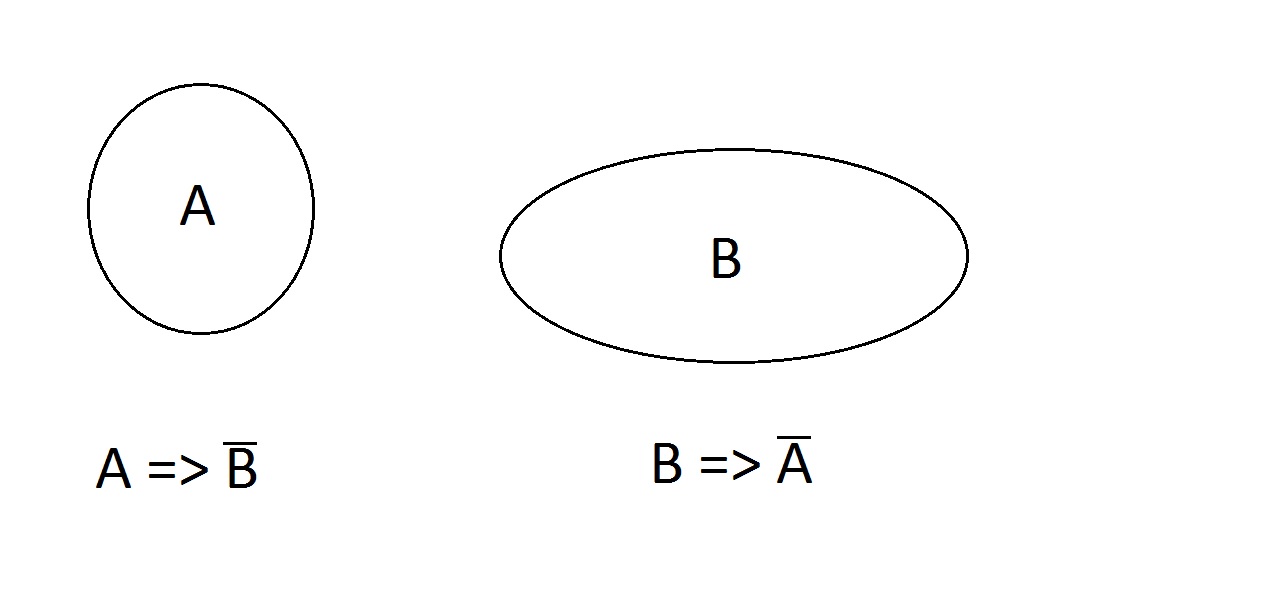
Hvad med dette. Egenskaberne er eksklusive; en entitet kan ikke have begge på samme tid. den kan have ingen, A eller B, men ikke AB. Udsagnene A=> ikke B og B => ikke A er gyldige.
Endeligt ønsker vi, at vores argumentation skal være sund. For at dette kan ske, skal argumentet være deduktivt gyldigt som ovenfor, og præmisserne skal være sande i den virkelige verden. Det betyder, at alle sunde argumenter er gyldige, men at alle gyldige argumenter ikke nødvendigvis er sunde.

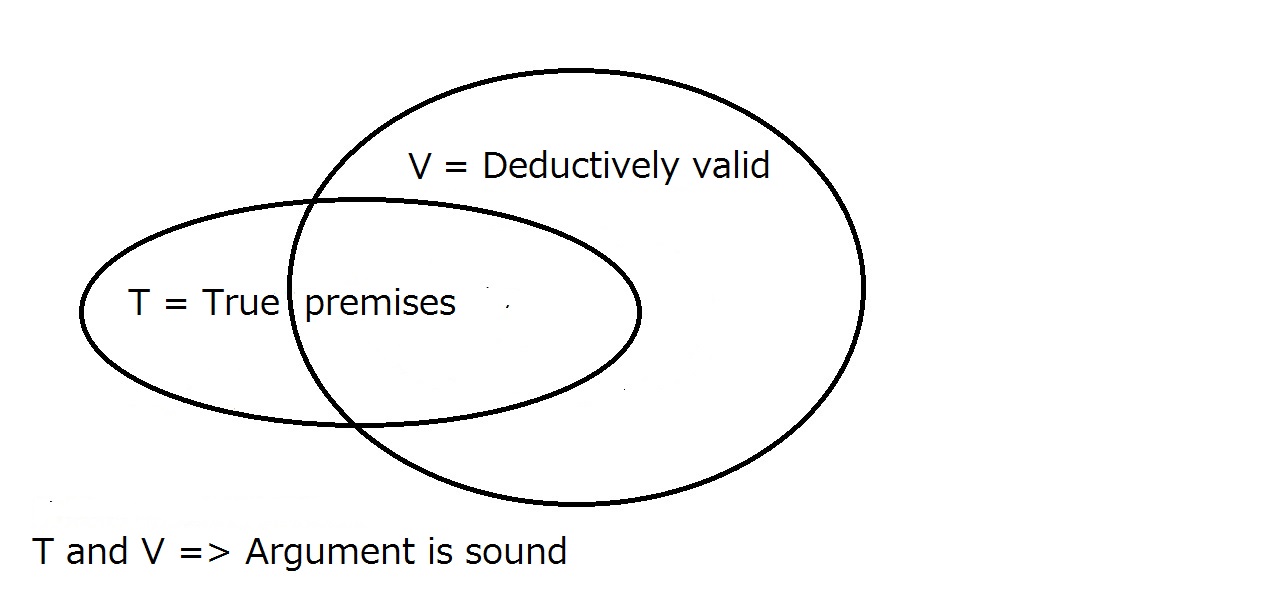
Et sundt argument kræver, at det er deduktivt gyldigt og har sande forudsætninger.At have det ene er ikke automatisk en garanti for det andet. Det område, der ligger inden for bådeT og V, er området for sunde argumenter.

Her er den måde, jeg ser det på. Alle lytter til mig.

Aristoteles (384-322 f.Kr.)

Fra http://www.rwe.org/images/aristotle.jpgExperiment?
Selvkonsistent?
Hvis din teori ikke er selvkonsistent, eller hvis din teori er uoverensstemmende med forsigtige eksperimenter, så er din teori forkert. Det er ligegyldigt, hvor smuk teorien er; den er forkert.

Galileo Galilei (1564-1642)

Fra http://helios.gsfc.nasa.gov/galileo.jpg

f.eks. Euklids femte postulat.

(1) Gennem to forskellige punkter er det muligt at trække én linje.
(2) En endelig ret linje kan forlænges kontinuerligt i en lige linje.
(3) En cirkel kan beskrives med et vilkårligt punkt som centrum og en vilkårlig afstand som radius.
(4) Alle rette vinkler er lige store.
(5) Gennem et givet punkt kan der kun trækkes én linje parallelt med en given linje.
Og ordene “punkt” og “linje” har ingen iboende betydning.
Man kunne bytte om på “punkt” og “linje” og stadig have sande sætninger.
Man kunne sige
(1) Gennem to vilkårlige forskellige blargs er det muligt at tegne en fleem…
Det femte postulat kan ændres på to måder:
(5) Gennem et givet punkt kan der ikke trækkes nogen linje parallelt med en given linje.
(5) Gennem et givet punkt kan der trækkes mange linjer parallelt med en given linje.
Både disse nye postulater giver anledning til forskellige KONSISTENTE geometrier.Hvilken af dem er rigtig? De er det alle sammen! Hvilken geometri beskriver universet?Det er Fysik!