Professor Fishers Notizen zu diesem Thema im PDF
Professor Fishers Folien zu diesem Thema im PDF (Passwort erforderlich)
Alte Folien von Professor Sekula im PDF.

Induktion

Anmerkung: Philosophen (einschließlich Prof. Fisher) unterscheiden zwischen Induktion (Verallgemeinerung der Eigenschaften einer bestimmten Stichprobe auf andere Dinge) und Abduktion (Rückschluss auf die beste Erklärung), während der folgende Inhalt beide unter der einzigen Überschrift „Induktion“ zusammenfasst. Wenn Sie diese Vorlesung bei Professor Fisher besuchen, sollten Sie sich lieber auf seine Notizen oder Folien zu diesem Thema verlassen als auf den unten stehenden Inhalt.

Induktion ist ein Prozess, bei dem man versucht, die Funktionsweise eines bestimmten Phänomens zu verstehen, indem man eine Stichprobe davon untersucht. Man arbeitet mit einer Stichprobe, weil es nicht möglich ist, alle Komponenten des Phänomens zu untersuchen. Der Wissenschaftler muss eine Probe eines Phänomens sorgfältig untersuchen und dann eine Hypothese formulieren, um das Phänomen zu erklären.Der wissenschaftliche Prozess des Testens der Hypothese folgt.Wissenschaftler, die die spektakulärsten Forschungsergebnisse erzielen, sind diejenigen, die kreativ genug sind, um sich die richtigen Forschungsfragen auszudenken.

Naturwissenschaften (Physik, Chemie, Biologie usw.) sind induktiv.Beweise werden gesammelt. Man beginnt mit konkreten Ergebnissen (einer Stichprobe) und versucht, die allgemeinen Regeln zu erraten. Hypothesen können nur widerlegt, niemals bewiesen werden. Hält eine Hypothese wiederholten Versuchen durch viele unabhängige Forscher stand, wächst das Vertrauen in die Hypothese. Alle Hypothesen sind vorläufig; jede könnte morgen widerlegt werden, aber es sind sehr starke Beweise erforderlich, um ein „Gesetz“ oder eine „Tatsache“ zu widerlegen.

Spezifisch -> Allgemein

Hier ein Beispiel für Induktion: Angenommen, ich habe 20 Murmeln zufällig aus einem großen Sack Murmeln genommen. Jede einzelne von ihnen ist weiß. Das ist meine Beobachtung – jede Murmel, die ich herausgenommen habe, war weiß. Ich könnte also die Hypothese aufstellen, dass dies erklärt werden könnte, wenn alle Murmeln in dem Beutel weiß wären. Um die Hypothese zu überprüfen, wären weitere Stichproben erforderlich.

Es könnte sein, dass sich einige verschiedenfarbige Murmeln in der Tüte befinden und meine erste Stichprobe einfach keine getroffen hat.

In diesem Fall könnten wir die Hypothese beweisen.

Wir könnten einfach alle Murmeln aus der Tüte herausnehmen und jede einzelne untersuchen.Ein solches Verfahren nennt man eine Zählung – wir schauen uns jede einzelne an. In den meisten Fällen, in denen Induktion verwendet wird, ist eine Zählung nicht durchführbar.

Abduktion: Inferenz auf die beste Erklärung

Dies ist eine Methode der Argumentation, die nicht so streng ist wie die Deduktion.Angenommen, Sie haben ein interessantes Ereignis beobachtet. Sie sind sich nicht sofort sicher, was diese Beobachtungen erklärt. Sie denken über alle möglichen Hypothesen nach, die die Beobachtungen plausibel erklären könnten – ein kreativer Prozess im Gegensatz zur Deduktion. Sie müssen so viel wie möglich über die Situation wissen, damit dies gut funktioniert. In Anbetracht all dessen, was Sie wissen, wählen Sie die Hypothese aus, die Ihnen am plausibelsten und wahrscheinlichsten erscheint.Sie haben die scheinbar beste Erklärung gewählt, auch wenn sie falsch sein könnte. Eine weitere Überprüfung Ihrer Erklärung ist normalerweise eine gute Idee, wenn es möglich ist; Sie könnten weitere Informationen finden, die Sie dazu bringen könnten, Ihre Schlussfolgerung zu überdenken.

Diese Art des Denkens ist die Stärke von Sherlock Holmes. Conan Doyles berühmt-berüchtigter hyper-aufmerksamer Detektiv bemerkt sogar winzige Hinweise, die der Polizeiinspektor normalerweise übersieht. Holmes kombiniert diese Hinweise mit dem allgemeinen Wissen, das er über den Fall gesammelt hat, und kommt so auf die beste Erklärung: Wer ist der Mörder? Er erklärt auch, wie das Verbrechen begangen wurde. Als nette Zugabe für den Leser erklärt Holmes oft die Überlegungen, die ihn zur Lösung des Falles geführt haben. Es scheint einfach, wenn Holmes es erklärt…

Deduktion

Mathematik ist eine deduktive Wissenschaft. Axiome werden vorgeschlagen. Sie werden nicht geprüft, sondern als wahr angenommen. Theoreme werden aus den Axiomen abgeleitet. Ausgehend von den Axiomen und den Regeln der Logik könnte eine Maschine Theoreme produzieren.

Allgemeines ->Besonderes

Beginne mit der allgemeinen Regel und leite spezifische Ergebnisse ab.

Wenn die Menge der Axiome ein Theorem und seine Verneinung hervorbringt, nennt man die Menge der Axiome INKONSISTENT.

Angenommen, wir haben die folgenden bekannten Bedingungen.

• Wir haben eine große Tüte Murmeln.
• Alle Murmeln in der Tüte sind bekanntermaßen weiß.
• Ich habe eine Zufallsstichprobe von 20 Murmeln aus der Tüte entnommen.

Aus diesen Murmeln kann ich schließen, dass alle Murmeln in der Stichprobe weiß sind, auch ohne sie zu betrachten. Diese Art des Schlussfolgerns nennt man modus ponens (mehr dazu weiter unten und in den Notizen von Prof. Fisher).

Wie wäre es damit?

• Wir haben einen großen Beutel mit Murmeln.
• Alle Murmeln in der Tüte sind weiß.
• Ich habe eine Probe von 20 Murmeln gemischter Farbe.

Daraus schließe ich schnell, dass die Probe nicht aus der Tüte mit den weißen Murmeln genommen wurde. Diese Art des Schlussfolgerns nennt man modus tollens (mehr dazu weiter unten und in den Notizen von Prof. Fisher).

Deduktive Argumente

Lassen Sie uns einen Blick auf die Idee des deduktiven Schlussfolgerns werfen (aus den Notizen von Prof. Fisher).Hier geht es darum, ein Argument für eine Idee oder eine Schlussfolgerung zu finden, die auf einer Reihe von Prämissen (Fakten, Ideen usw.) beruht. Prof. Fisher merkt an, dass Philosophen dies gewöhnlich wie folgt darstellen:

1. Premise number 12. Premise number 2...------------------------C. Conclusion to be reached

Diese Struktur stellt ein Argument dar.Manchmal wird es geschrieben als
Prämisse 1, Prämisse 2, Prämisse… => Schlussfolgerung.
Kürzen wir dies zu einem Syllogismus ab:
P => C (Prämissen implizieren Schlussfolgerung, genau wie oben)
Das bedeutet einfach, dass, wenn die Prämissen wahr sind, die Schlussfolgerung ebenfalls wahr ist.
„Um gut zu sein, muss ein Argument wahre Prämissen haben und die Prämissen müssen die Schlussfolgerung unterstützen. Die stärkstmögliche Unterstützung würde eine absolute Garantie dafür bieten, dass die Schlussfolgerung wahr ist (natürlich unter der Voraussetzung, dass die Prämissen wahr sind).Wir werden diese Art der Unterstützung zuerst betrachten, dann aber auch einige schwächere Arten der Unterstützung in Betracht ziehen.“ (von Prof. Fisher)
Eine besonders nützliche Art von Argumenten ist ein deduktiv gültiges Argument. (Dies wird oft als „gültiges Argument“ oder manchmal als „deduktives Argument“ abgekürzt.)Deduktiv gültige Argumente sind Argumente, bei denen die Prämissen, wenn sie wahr wären, der stärkste mögliche Beweis dafür wären, dass die Schlussfolgerung wahr ist. Diese Argumente bieten nämlich folgende Garantie: Wenn die Prämissen wahr sind, dann muss auch die Schlussfolgerung wahr sein.
Ein Argument, das deduktiv zu sein scheint, aber Prämissen hat, die die Schlussfolgerung nicht unterstützen (keine Garantie), ist ein ungültiges Argument.
Wiederholen wir den Syllogismus P => C (Prämissen führen zur Schlussfolgerung).Es gibt vier mögliche Behauptungen, die man dazu aufstellen könnte:

1. Alle Prämissen sind wahr (P ist wahr) (modus ponens Argumentation)
2. Eine oder mehrere der Prämissen ist falsch (P ist falsch – nicht P)
3. Die Konklusion ist wahr (C ist wahr)
4. Die Konklusion ist falsch (C ist falsch – nicht C) (Modus-Tollens-Schluss)

Nur zwei davon (#1 und #4) stellen deduktiv gültige Schlussfolgerungen dar.Schauen wir uns den Grund dafür an, eine Auswahl nach der anderen.

1. P ist wahr (P) – Bestätigung des Vorangegangenen. Wenn alle Prämissen wahr sind, muss auch die Schlussfolgerung wahr sein. Dies ist ein sehr starkes Argument. (modus ponens)
2. P ist falsch (nicht P) – Leugnen des Vorangegangenen. Dass P falsch ist, garantiert nicht, dass C entweder wahr oder falsch ist. Es könnte andere Ursachen geben.
3. C ist wahr (C) – Bejahung der Konsequenz. Wenn C wahr ist, kann es aus einem von mehreren Gründen sein, nicht aus diesem spezifischen P.
4. C ist falsch (nicht C) – Verneinung der Konsequenz. Hier, wenn C falsch ist, dann muss P auch falsch sein. Wenn P wahr wäre, dann wäre auch C wahr. (modus tollens)

Kurz gesagt, #1 und #4 (modus ponens und modus tollens) sind deduktiv gültig, während #2 und #3 es nicht sind.
Wenn die Prämissen auf Dinge in der realen Welt zutreffen, muss man immer noch einen Test auf Ungültigkeit durchführen. Es gibt mindestens drei Ansätze.

1. Sieh nach, ob du ein Szenario finden kannst, in dem die Prämissen wahr sind, aber die Schlussfolgerung falsch ist.
2. Versuch, ein Substantiv oder Adjektiv im Argument durch ein anderes zu ersetzen.Ersetze alle Instanzen. Wenn dies offensichtlich nicht gültig ist, dann war das Original nicht gültig.
3. Stellen Sie P und C in einem Venn-Diagramm dar.
4. Wenn Sie dies so tun können, dass P wahr, C aber falsch ist, ist das Argument ungültig. Wir haben diese Diagramme für dich unten erstellt.

Nun kommen wir zum Thema Venn-Diagramme. Diese können bei der Überprüfung der Prämissen eines Arguments von großem Wert sein.

Venn-Diagramme

Venn-Diagramme sind eine grafische Methode zur Darstellung der Logik.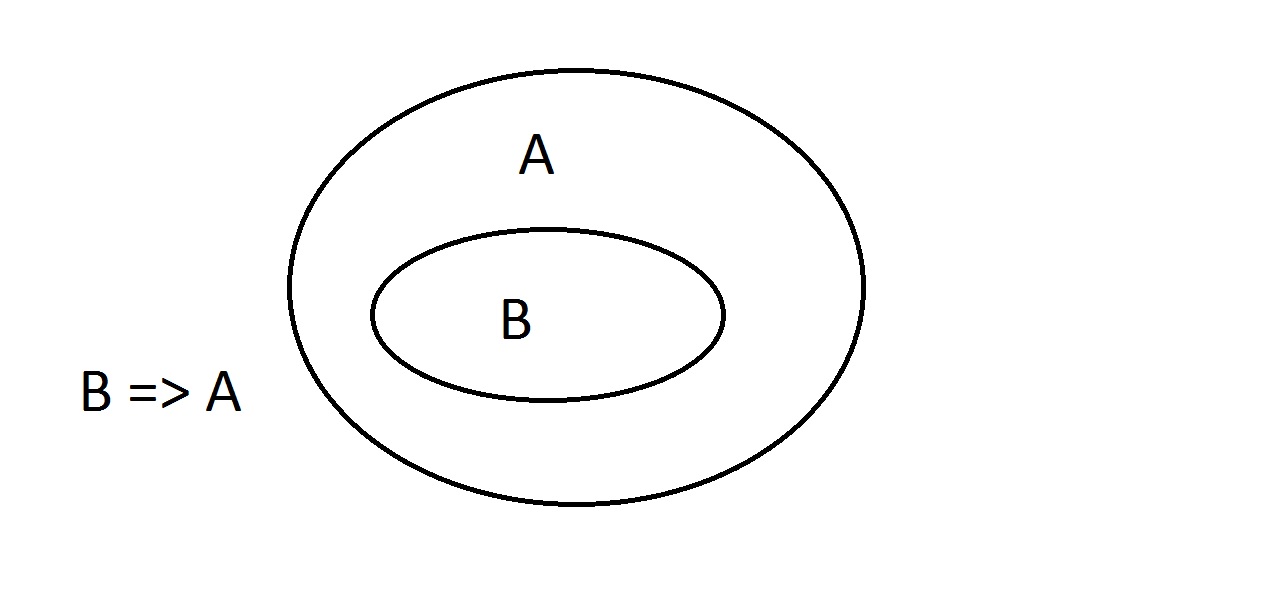
Dies ist so ziemlich das einfachste Diagramm, das man bekommen kann. Das äußere Oval enthält alle Dinge, die die Eigenschaft A haben, während das innere Oval alle Dinge enthält, die sowohl die Eigenschaft B als auch die Eigenschaft A haben.Dies wird als B=>A dargestellt, was bedeutet, dass alle Dinge, die die Eigenschaft B haben, auch die Eigenschaft A haben.Man könnte auch sagen: „B impliziert A. „Wenn B wahr ist, dann muss auch A wahr sein. Dies ist die oben erwähnte Garantie.
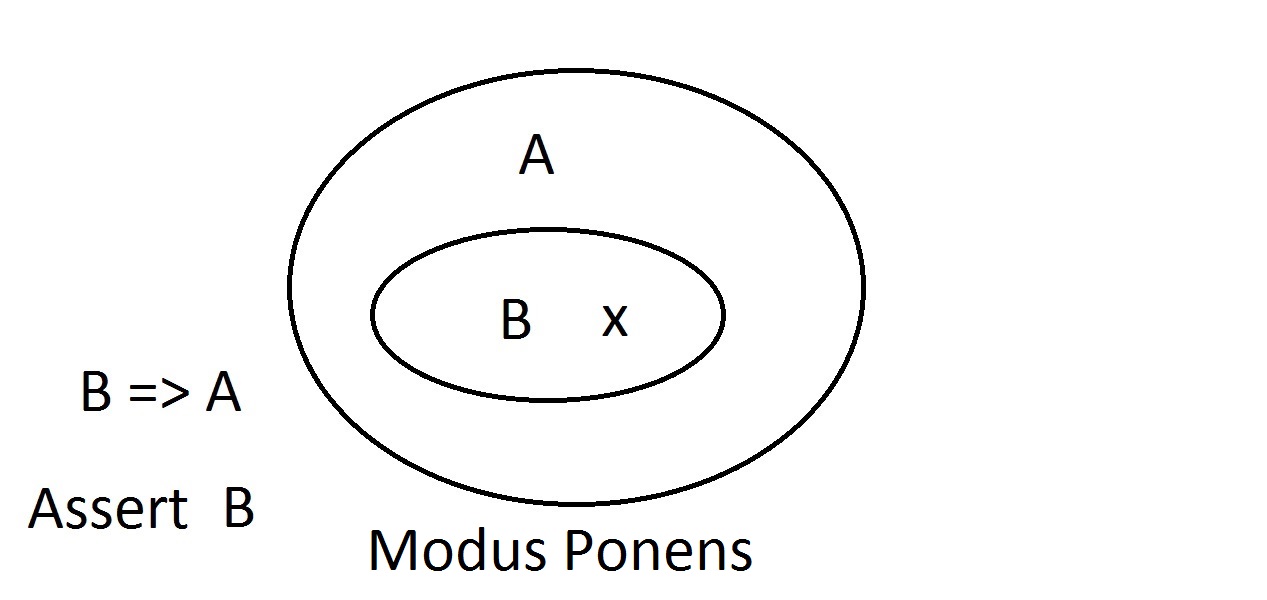Wir werden nun behaupten, dass wir etwas mit der Eigenschaft B haben. Wir können getrost behaupten, dass es auch die Eigenschaft A hat. Dies ist Modus Ponens (Bejahung des Vorangehenden). Jede Entität mit der Eigenschaft B muss sich offensichtlich auch im Raum der Eigenschaft A befinden.
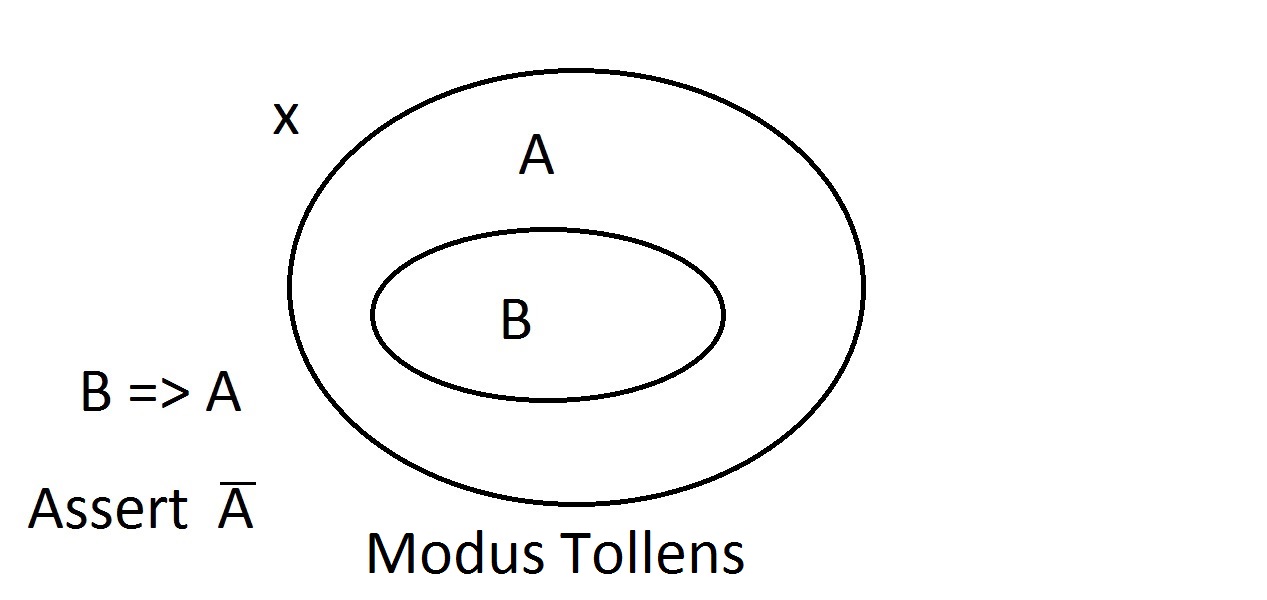Angenommen, wir behaupten nun, dass eine Entität die Eigenschaft A nicht hat. Das Venn-Diagramm zeigt, dass sie auch nicht die Eigenschaft B haben kann. Alles, was außerhalb des Raums der Eigenschaft A liegt, muss auch außerhalb des Raums der Eigenschaft B liegen. Dies ist eine Modus-Tollens-Schlussfolgerung und ist gültig und stark.
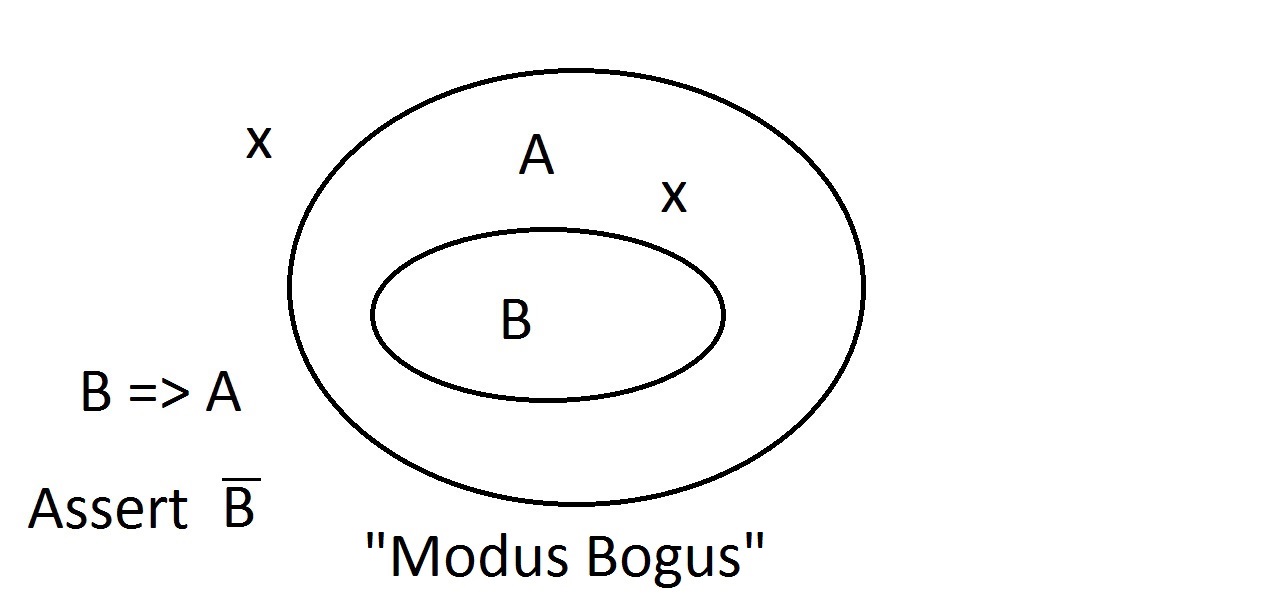Nun werden wir versuchen zu behaupten, dass unser Ding die Eigenschaft B nicht besitzt. Ein Blick auf das Venn-Diagramm zeigt hier das Problem. Ein Ding, das die Eigenschaft B nicht besitzt, kann innerhalb des A-Raums liegen oder außerhalb desselben. Die Behauptung „nicht B“ sagt uns nichts über A. Das ist keine gültige Argumentation, deshalb haben wir es Modus Bogus genannt. Es ist ein Leugnen des Antezedens und nicht gültig.
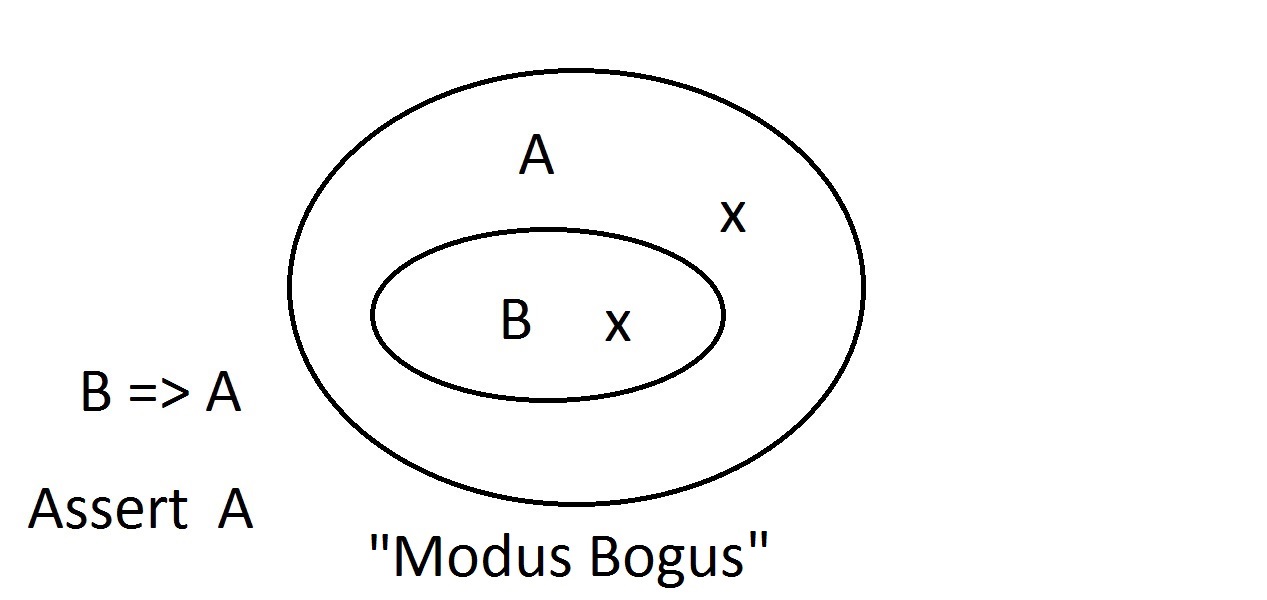Die letzte Möglichkeit ist die Behauptung, dass unser Ding die Eigenschaft A hat.Das Venn-Diagramm zeigt das Problem. Das Ding könnte überall im Raum A liegen, entweder innerhalb oder außerhalb des Raums B. Die Behauptung, dass das Ding die Eigenschaft A hat, sagt nichts darüber aus, ob es auch die Eigenschaft B hat. Dies ist auch ein Modus Bogus oder eine ungültige Argumentation, die als Affirmation der Konsequenz bezeichnet wird.
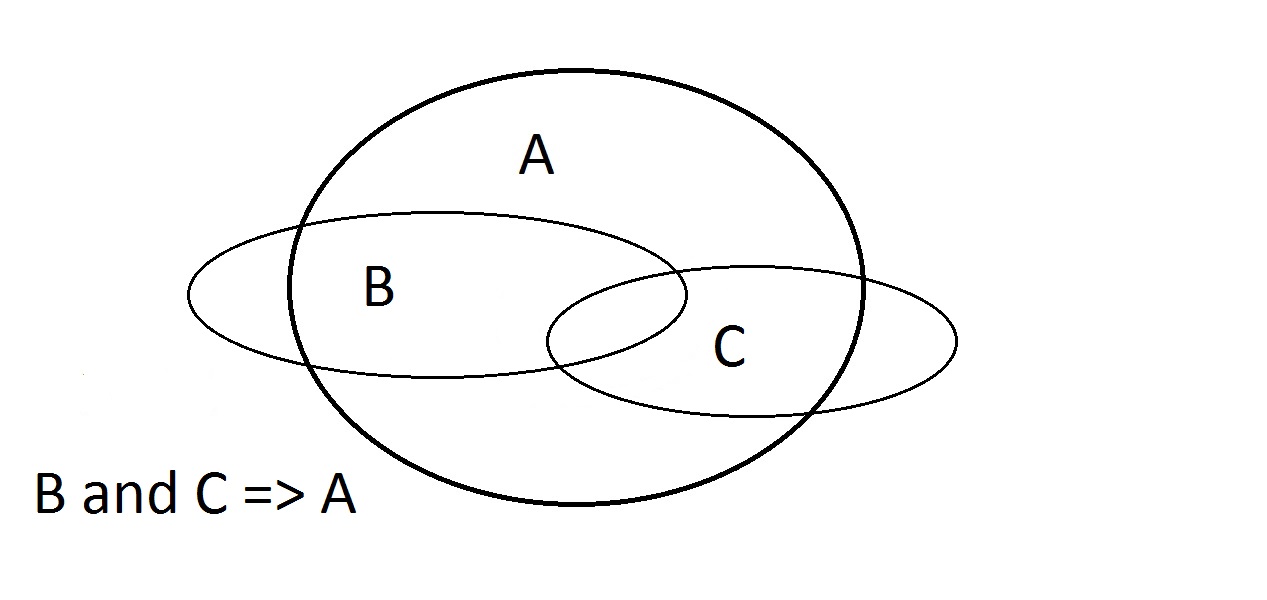Hier haben wir es mit den Eigenschaften A, B und C zu tun.Hier können wir nur garantieren, dass eine Entität, die B und C hat, auch A hat.Beachten Sie, dass einige der Räume B und C außerhalb von A liegen.

• Behauptung A: Könnte überall in A sein
• Behauptung B: Ein Teil von B liegt außerhalb von A
• Behauptung C: Ein Teil von C liegt außerhalb von A
• Behauptung A und B: Könnte ein Teil von C enthalten; vielleicht auch nicht.
• Behauptung B und C: Der Schnittpunkt BC liegt vollständig in A. Die Behauptung, dass B und C => A ist, funktioniert.
• Behauptung A und C: Kann etwas B enthalten; kann nicht sein

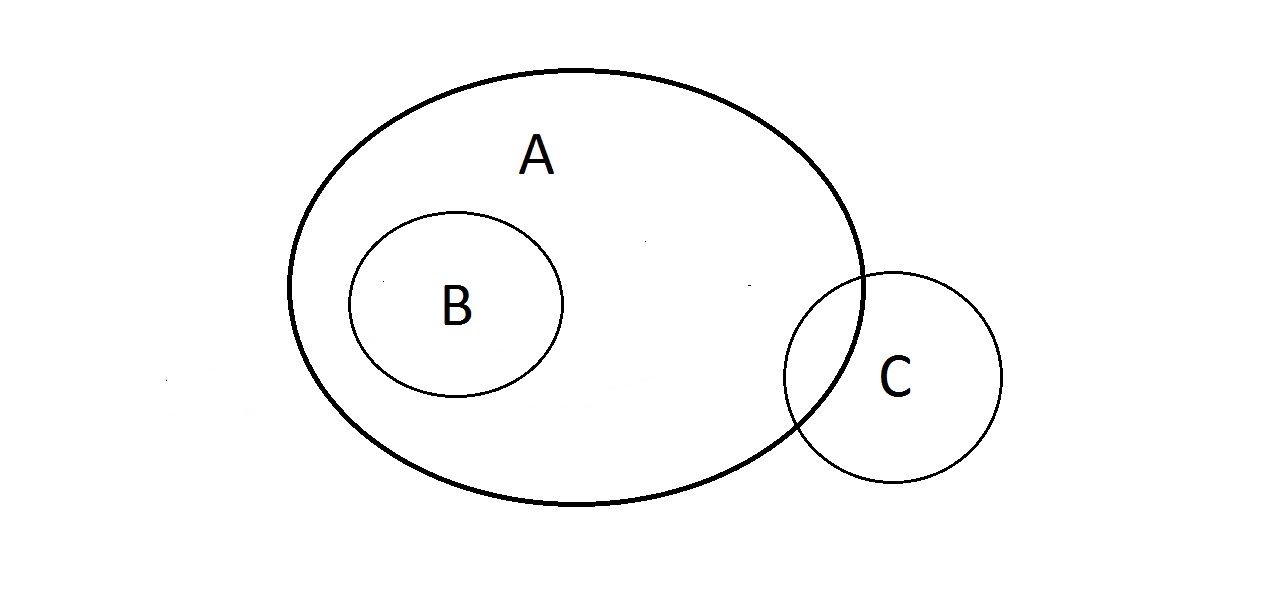
Was kann man damit machen? Die Eigenschaften A und B sind wie oben, aber was ist mit C? Etwas, das die Eigenschaft C hat, kann in A liegen oder auch nicht. Etwas in A könnte auch in C sein oder auch nicht. Mit C kann man hier nichts anfangen. Wir haben aber die Garantie, dass etwas, das B hat, auch A hat.

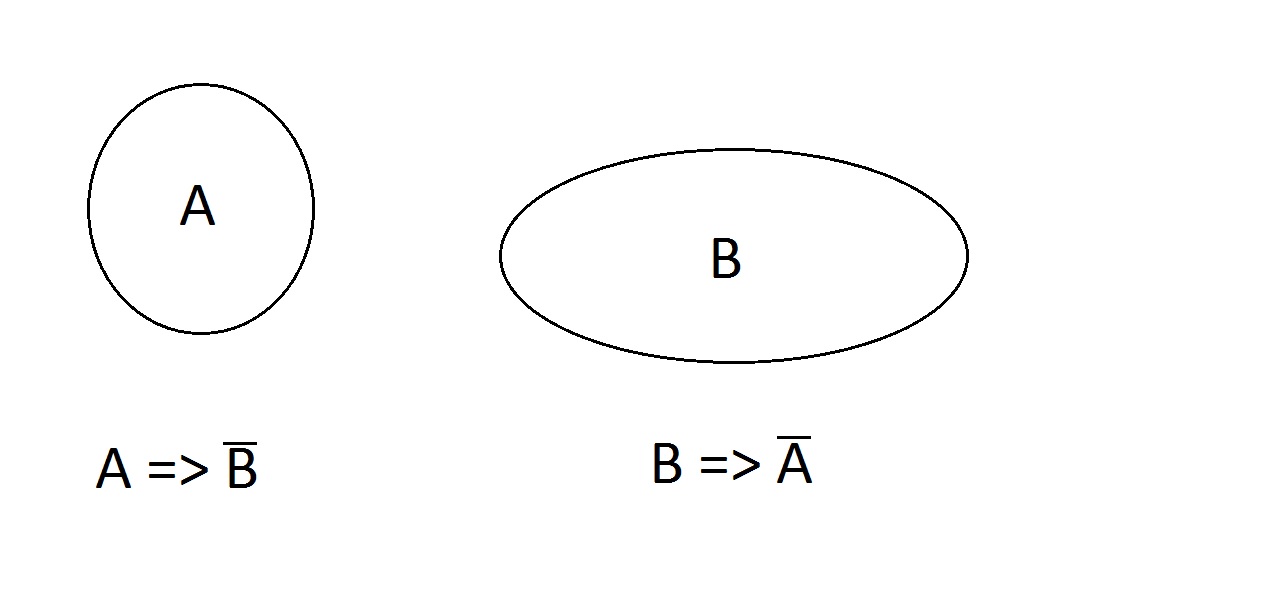
Wie wäre es damit. Die Eigenschaften schließen sich aus; eine Entität kann nicht beides gleichzeitig haben, sie kann weder A noch B haben, aber nicht AB. Die Aussagen A=> nicht B und B => nicht A sind gültig.
Schließlich wollen wir, dass unser Argument stichhaltig ist. Dazu muss das Argument wie oben beschrieben deduktiv gültig sein und die Prämissen müssen in der realen Welt wahr sein. Das bedeutet, dass alle stichhaltigen Argumente auch stichhaltig sind, aber nicht alle stichhaltigen Argumente sind notwendigerweise stichhaltig.

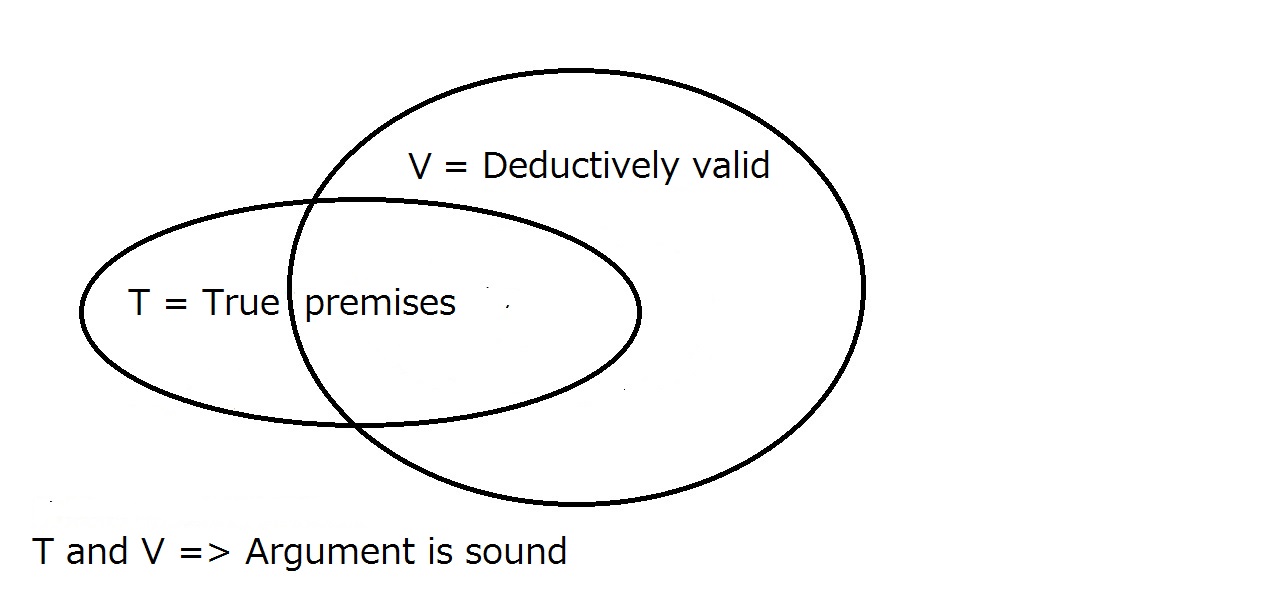
Ein stichhaltiges Argument erfordert, dass es deduktiv gültig ist und wahre Prämissen hat.Das eine garantiert nicht automatisch das andere. Der Bereich, der sowohl in T als auch in V liegt, ist der Bereich der stichhaltigen Argumente.

So sehe ich das. Hört mir alle zu.

Aristoteles (384-322 v. Chr.)

Von http://www.rwe.org/images/aristotle.jpgExperiment?
Selbstkonsistent?
Wenn deine Theorie nicht selbstkonsistent ist, oder deine Theorie nicht mit sorgfältigen Experimenten übereinstimmt, dann ist deine Theorie falsch. Es spielt keine Rolle, wie schön die Theorie ist; sie ist falsch.

Galileo Galilei (1564-1642)

Aus http://helios.gsfc.nasa.gov/galileo.jpg

z.B. Euklids fünftes Postulat.

(1) Durch zwei beliebige Punkte kann man eine Linie ziehen.
(2) Eine endliche Gerade kann in einer Geraden kontinuierlich verlängert werden.
(3) Ein Kreis kann mit einem beliebigen Punkt als Mittelpunkt und einer beliebigen Strecke als Radius beschrieben werden.
(4) Alle rechten Winkel sind gleich.
(5) Durch einen gegebenen Punkt kann nur eine Linie parallel zu einer gegebenen Linie gezogen werden.
Die Worte „Punkt“ und „Linie“ haben keine eigentliche Bedeutung.
Man könnte „Punkt“ und „Linie“ vertauschen und hätte immer noch wahre Theoreme.
Man könnte sagen
(1) Durch zwei beliebige Punkte kann man eine Linie ziehen…
Das fünfte Postulat kann auf zwei Arten geändert werden:
(5) Durch einen gegebenen Punkt kann keine Linie parallel zu einer gegebenen Linie gezogen werden.
(5) Durch einen gegebenen Punkt können viele Linien parallel zu einer gegebenen Linie gezogen werden.
Beide dieser neuen Postulate führen zu unterschiedlichen KONSTANTEN Geometrien.Welches ist richtig? Sie sind es alle! Welche beschreibt das Universum?Das ist die PHYSIK!