Aantekeningen van professor Fisher over dit onderwerp in PDF
Dia’s van professor Fisher over dit onderwerp in PDF (wachtwoord vereist)
Old dia’s van professor Sekula in PDF.

Inductie

Noot: Filosofen (waaronder prof. Fisher) maken onderscheid tussen inductie (het veralgemenen van de eigenschappen van een bepaald monster naar andere dingen) en abductie (het gevolgtrekken naar de beste verklaring), terwijl in de inhoud hieronder beide zaken worden samengevoegd onder de noemer “inductie”. Als u deze cursus volgt bij professor Fisher, kunt u zich beter baseren op zijn aantekeningen of dia’s over dit onderwerp, dan op de inhoud hieronder.

Inductie is een proces waarbij men probeert de werking van een verschijnsel te achterhalen door een steekproef ervan te bestuderen. Je werkt met een steekproef omdat het niet haalbaar is om elke component van het verschijnsel te bekijken.Inductie is een creatief proces. De wetenschapper moet een steekproef van een verschijnsel zorgvuldig bestuderen en dan een hypothese formuleren om het verschijnsel te verklaren.Het wetenschappelijke proces van het testen van de hypothese volgt.Wetenschappers die de meest spectaculaire onderzoeksresultaten behalen, zijn degenen die creatief genoeg zijn om de juiste onderzoeksvragen te bedenken.

Natuurwetenschappen (natuurkunde, scheikunde, biologie, enz.) zijn inductief.Bewijsmateriaal wordt verzameld. De wetenschappelijke methode wordt toegepast.Begin met specifieke resultaten (een steekproef) en probeer de algemene regels te raden. Hypothesen kunnen alleen worden weerlegd, nooit bewezen. Als een hypothese bestand is tegen herhaalde proeven door vele onafhankelijke onderzoekers, dan groeit het vertrouwen in de hypothese. Alle hypothesen zijn voorlopig; elke hypothese kan morgen weerlegd worden, maar er is zeer sterk bewijs nodig om een “Wet” of “Feit” omver te werpen.

Specifiek -> Algemeen

Hier volgt een voorbeeld van inductie: Stel, ik heb 20 knikkers willekeurig uit een grote zak knikkers genomen. Ze bleken allemaal wit te zijn. Dat is mijn waarneming – elke knikker die ik eruit haalde was wit. Ik kan dus de hypothese stellen dat dit te verklaren is als alle knikkers in de zak wit zijn. Verdere steekproeven zouden nodig zijn om de hypothese te testen. Het zou kunnen dat er enkele knikkers met verschillende kleuren in de zak zitten en dat mijn eerste steekproef er gewoon geen heeft geraakt.

Toevallig is dit een geval waarin we de hypothese kunnen bewijzen. We zouden eenvoudig alle knikkers in de zak kunnen dumpen en ze stuk voor stuk onderzoeken. Een dergelijke procedure wordt een telling genoemd – bekijk ze allemaal. In de meeste gevallen waarin inductie wordt gebruikt, is een telling niet haalbaar.

Abductie: Induceren tot de beste verklaring

Dit is een redeneermethode die niet zo rigoureus is als Deductie.Stel dat u waarnemingen hebt van een interessant voorval. U bent niet onmiddellijk zeker wat de waarnemingen verklaart. Je bedenkt alle mogelijke hypotheses die de waarnemingen plausibel zouden kunnen verklaren. Dit is een creatief proces, in tegenstelling tot deductie. Je moet zo veel mogelijk over de situatie weten om dit goed te laten werken. Gegeven alles wat je weet, kies je de hypothese die het meest redelijk en waarschijnlijk lijkt. Je hebt de schijnbaar beste verklaring gekozen, hoewel die fout kan zijn. Er is geen garantie. Verdere controle van uw verklaring is meestal een goed idee als het mogelijk is; u zou meer informatie kunnen vinden die u uw conclusie zou kunnen doen heroverwegen.

Dit soort redeneren is de forte van Sherlock Holmes. Conan Doyle’s beroemde hyper-observante detective merkt zelfs zeer kleine aanwijzingen die de politie-inspecteur meestal mist. Holmes combineert deze aanwijzingen met de algemene kennis die hij over de zaak heeft opgebouwd om tot de beste verklaring te komen – whodunit! Hij legt ook uit hoe de misdaad werd gepleegd. In een leuk extraatje voor de lezer, legt Holmes vaak de redenering uit die hem tot de oplossing leidde. Het lijkt eenvoudig als Holmes het uitlegt…

Deductie

Mathematica is een deductieve wetenschap. Axioma’s worden voorgesteld. Zij worden niet getoetst; zij worden voor waar aangenomen. Uit de axioma’s worden stellingen afgeleid. Gegeven de axioma’s en de regels van de logica, zou een machine stellingen kunnen produceren.

Algemeen -> Specifiek

Start met de algemene regel en leid specifieke resultaten af.Als de verzameling axioma’s een stelling en zijnnegatie oplevert, wordt de verzameling axioma’s INCONSISTENT genoemd.

Voorstel dat we de volgende bekende voorwaarden hebben.

• We hebben een grote zak knikkers.
• Alle knikkers in de zak zijn wit.
• Ik heb een aselecte steekproef van 20 knikkers uit de zak.

Uit deze kan ik afleiden dat alle knikkers in de steekproef wit zijn, zelfs zonder ze te bekijken. Dit soort redeneren heet modus ponens (meer hierover hieronder en in de aantekeningen van Prof. Fisher).

Hoe zit het met dit?

• We hebben een grote zak knikkers.
• Alle knikkers in de zak zijn wit.
• Ik heb een monster van 20 knikkers van gemengde kleuren.

Hieruit leid ik snel af dat het monster niet genomen is uit de zak met witte knikkers. Dit soort redeneren heet modus tollens (meer hierover hieronder en in de aantekeningen van Prof. Fisher).

Deductieve Argumenten

Laten we eens kijken naar het idee van deductief redeneren (ontleend aan de aantekeningen van Prof. Fisher).Hier hebben we het over het maken van een argument voor een of ander idee of een of andere conclusie op basis van een reeks premissen (feiten, ideeën, enz.).Prof. Fisher merkt op dat filosofen dit gewoonlijk weergeven als

1. Premise number 12. Premise number 2...------------------------C. Conclusion to be reached

Deze structuur vormt een argument.Soms wordt het geschreven als
Premisse 1, Premisse 2, Premisse… => Conclusie.
Laten we dit als volgt afkorten tot het syllogisme:
P => C (Premissen impliceren Conclusie, net als hierboven)
Dit betekent simpelweg dat als de premissen waar zijn, de conclusie ook waar is.
“Om goed te zijn, moet een argument ware premissen hebben en de premissen moeten steun bieden aan de conclusie. De sterkst mogelijke ondersteuning zou een absolute garantie bieden dat de conclusie waar zal zijn (in de veronderstelling natuurlijk dat de premissen waar zijn). We zullen eerst dat soort ondersteuning bekijken, maar daarna zullen we ook enkele zwakkere vormen van ondersteuning bekijken.” (van Prof. Fisher)
Een bijzonder nuttig soort argument is een deductief geldig argument. (Dit wordt vaak afgekort als “geldig argument” of soms als “deductief argument”.)Deductief geldige argumenten zijn argumenten waarin de premissen, als ze waar zouden zijn, het sterkst mogelijke bewijs zouden zijn dat de conclusie waar is. Deze argumenten bieden namelijk de volgende garantie: als de premissen waar zijn, dan moet de conclusie ook waar zijn.
Een argument dat deductief lijkt, maar premissen heeft die de conclusie niet ondersteunen (geen garantie) is een ongeldigargument.
Laten we het syllogisme P => C herhalen (Premissen leiden tot conclusie).Er zijn vier mogelijke beweringen die je hierover zou kunnen doen:

1. Alle premissen zijn waar (P is waar) (modus ponens redeneren)
2. Eén of meer van de premissen is onwaar (P is onwaar -. niet P)
3. De conclusie is waar (C is waar)
4. De conclusie is onwaar (C is onwaar – niet C) (modus tollens redeneren)

Nauwelijks twee van deze (#1 en #4) vormen een deductief geldige redenering.Laten we de reden daarvan eens bekijken, één keuze tegelijk.

1. P is waar (P) – Bevestiging van het antecedent. Als alle premissen waar zijn, moet de conclusie ook waar zijn. Dit is een zeer sterk argument. (modus ponens)
2. P is onwaar (niet P) – Ontkenning van het antecedent. Dat P onwaar is, garandeert niet dat C waar of onwaar is. Er kunnen andere oorzaken zijn.
3. C is waar (C) – Bevestiging van het consequente. Als C waar is kan dat om een van meerdere redenen zijn, niet deze specifieke P.
4. C is onwaar (niet C) – Ontkenning van het consequente. Hier, als C onwaar is dan moetP ook onwaar zijn. Als P waar zou zijn, zou C dat ook zijn. (modus tollens)

In het kort, #1 en #4 (modus ponens en modus tollens) zijn deductief geldig, terwijl #2 en #3 dat niet zijn.
Als de premissen van toepassing zijn op dingen in de echte wereld, moet je nog steeds een ongeldigheidstoets doen. Er zijn minstens drie benaderingen.

1. Zie of je een scenario kunt vinden waarin de premissen waar zijn maar de conclusie onwaar.
2. Probeer eens een zelfstandig naamwoord of bijvoeglijk naamwoord in het argument te vervangen door een ander. Vervang alle gevallen. Als dit duidelijk niet geldig is, dan was het origineel niet geldig.
3. Voorstel P en C in een Venn-diagram.Als je dit zo kunt doen dat P waar is maar C onwaar, dan is het argument ongeldig. We hebben deze diagrammen hieronder voor u gemaakt.

Nu brengen we het onderwerp van Venn-diagrammen ter sprake. Deze kunnen van grote waarde zijn bij het controleren van de premissen van een argument.

Venn-diagrammen

Venn-diagrammen zijn een grafische methode om logica weer te geven.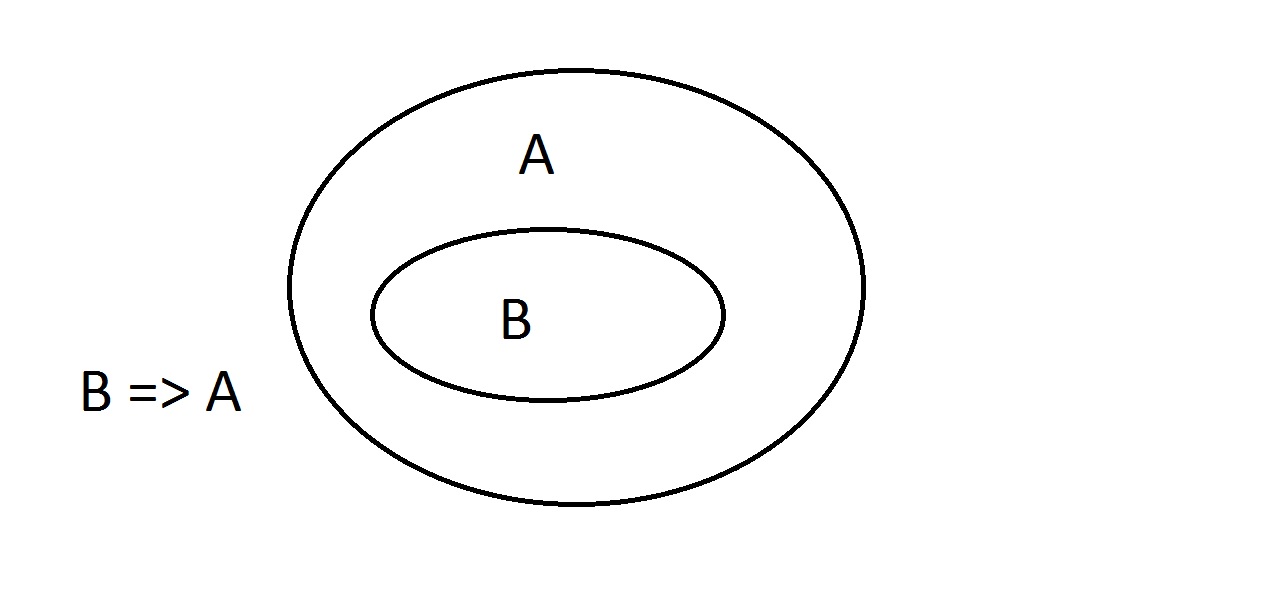
Dit is ongeveer het eenvoudigste diagram dat je zult krijgen. De buitenste ovaal bevat alle dingen die eigenschap A hebben, terwijl de binnenste ovaal alle dingen bevat die zowel eigenschap B als eigenschap A hebben. Dit wordt weergegeven als B=>A, wat betekent dat alle dingen die eigenschap B hebben ook eigenschap A hebben. Je zou ook kunnen zeggen “B impliceert A. “Als B waar is, dan moet A dat ook zijn. Dit is de hierboven genoemde garantie.
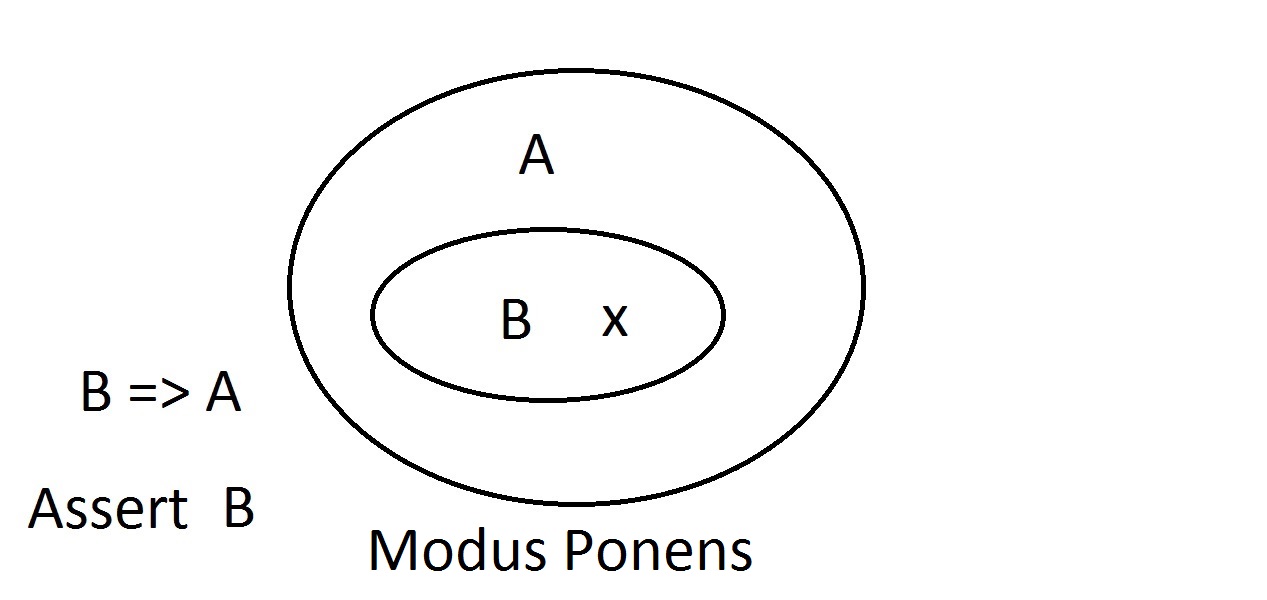We zullen nu beweren dat we iets hebben met eigenschap B. We kunnen met een gerust hart beweren dat het ook de eigenschap A heeft. Dit is Modus Ponens (bevestigen van het antecedent) redeneren. Elke entiteit met eigenschap B moet zich uiteraard ook in de ruimte voor eigenschap A bevinden.
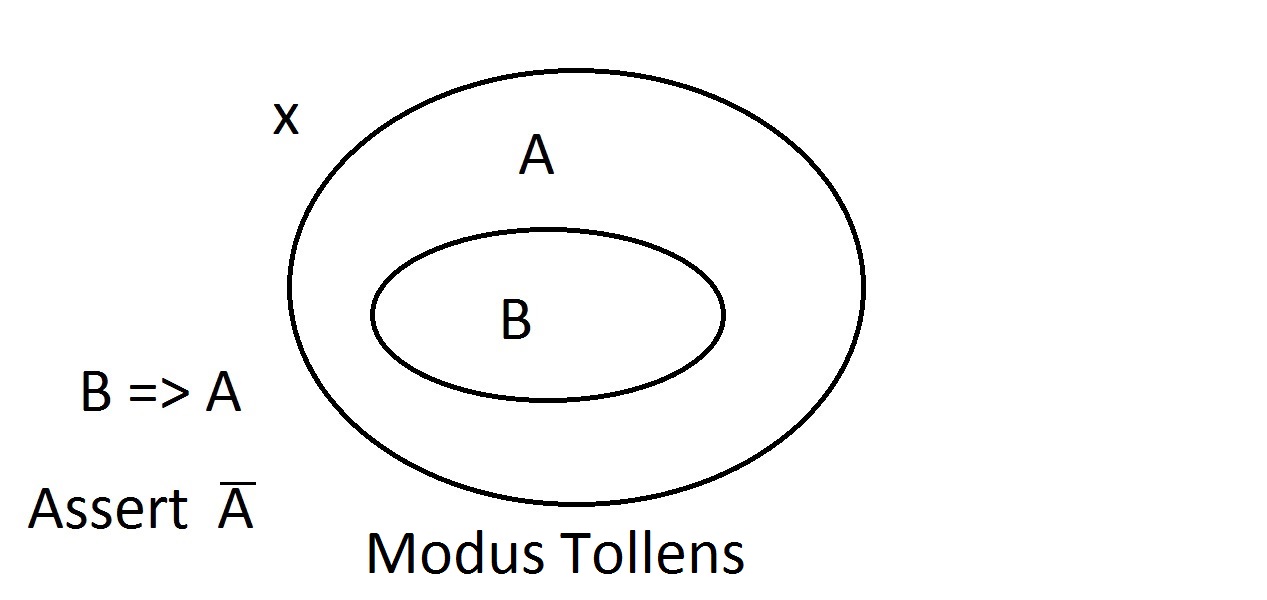Stel nu dat we beweren dat een entiteit eigenschap A niet heeft. Alles wat buiten de ruimte van eigenschap A ligt, moet ook buiten de ruimte van eigenschap B liggen. Dit is Modus Tollens (het gevolg ontkennen)-redeneren en het is geldig en sterk.
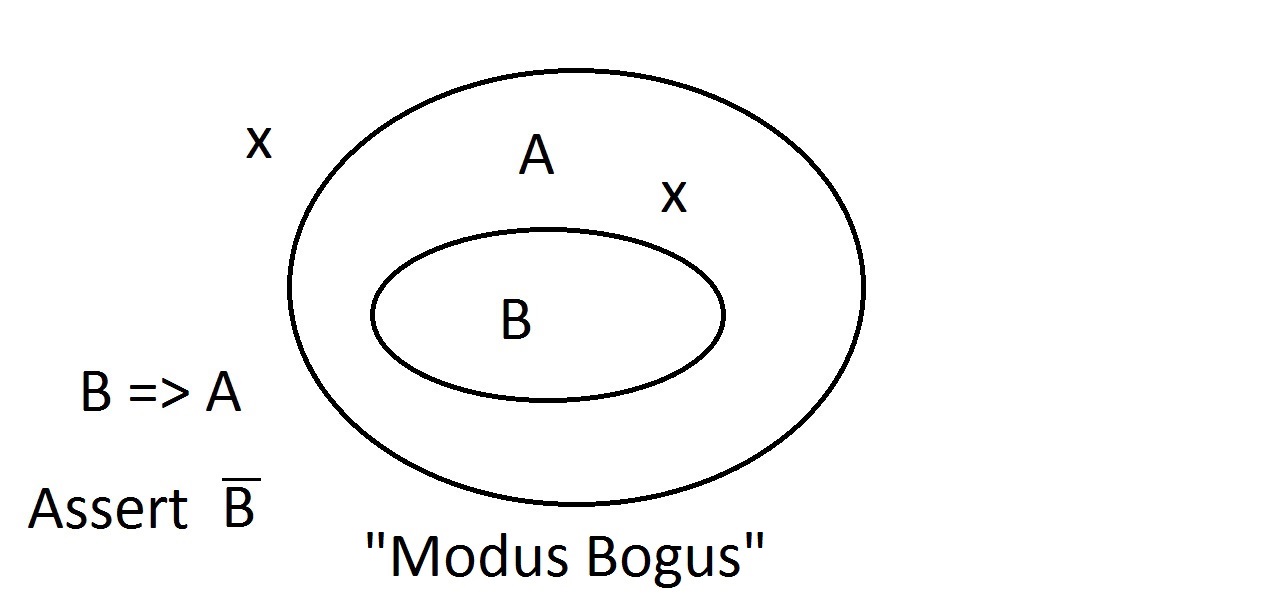Nu zullen we proberen te beweren dat ons ding eigenschap B niet bezit. Een blik op het Venn-diagram toont het probleem hier. Een entiteit die eigenschap B niet bezit, kan binnen of buiten de A-ruimte liggen. De bewering “niet B” zegt ons niets over A. Dit is geen geldige redenering, en daarom noemen we het Modus Bogus. Het is het ontkennen van het antecedent en is niet geldig.
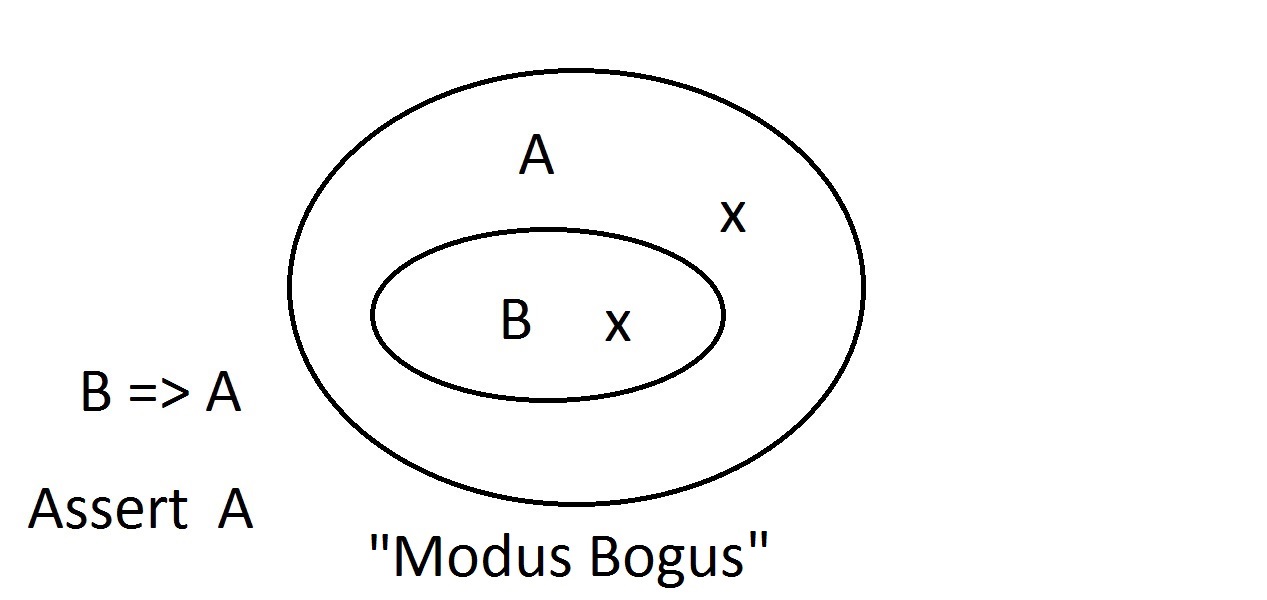De laatste mogelijkheid is de bewering dat ons ding eigenschap A heeft. De entiteit kan overal in de A-ruimte liggen, zowel binnen als buiten de B-ruimte. Beweren dat het ding eigenschap A heeft, zegt niets over de vraag of het ook B heeft. Dit is ook Modus Bogus, of ongeldig redeneren. Het heet Affirming the Consequent.
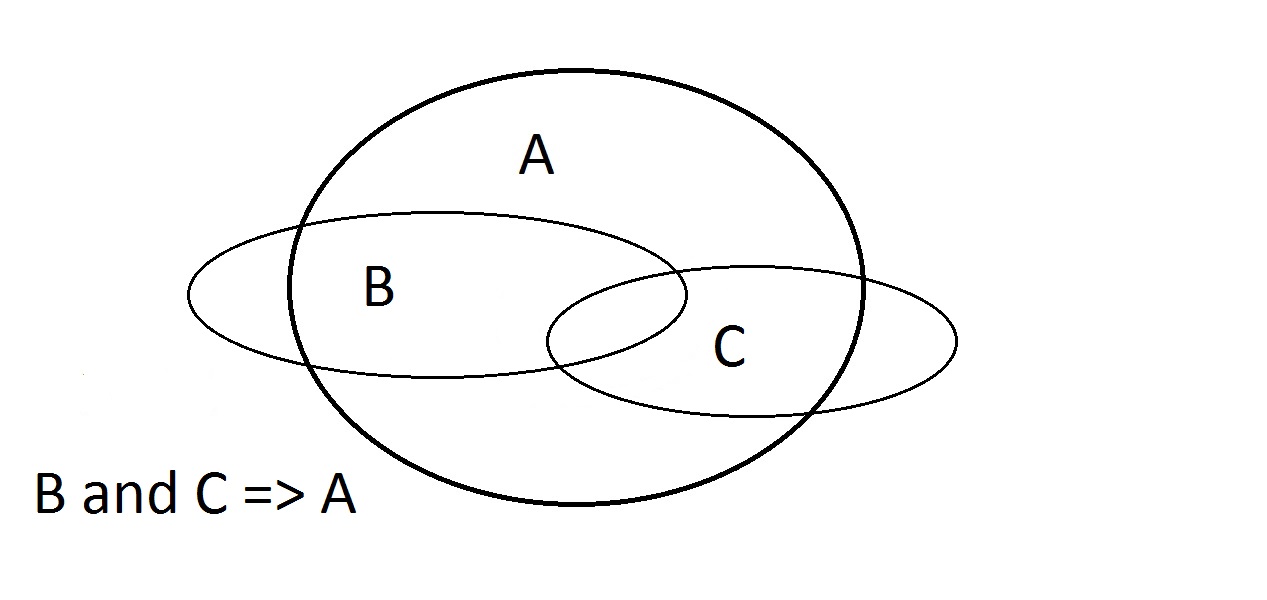Hier hebben we te maken met eigenschappen A, B en C. Hier kunnen we alleen garanderen dat een entiteit die B en C heeft, ook A heeft.Merk op dat sommige ruimtes van B en C buiten A liggen.

• Bevestig A: kan overal in A liggen
• Bevestig B: een deel van B ligt buiten A
• Bevestig C: een deel van C ligt buiten A
• Bevestig A en B: kan een deel van C omvatten; misschien ook niet.
• Bewering B en C: het snijpunt BC ligt geheel in A. Argumenteren dat B en C => A werkt.
• Bewering A en C: kan een deel B omvatten; mogelijk niet

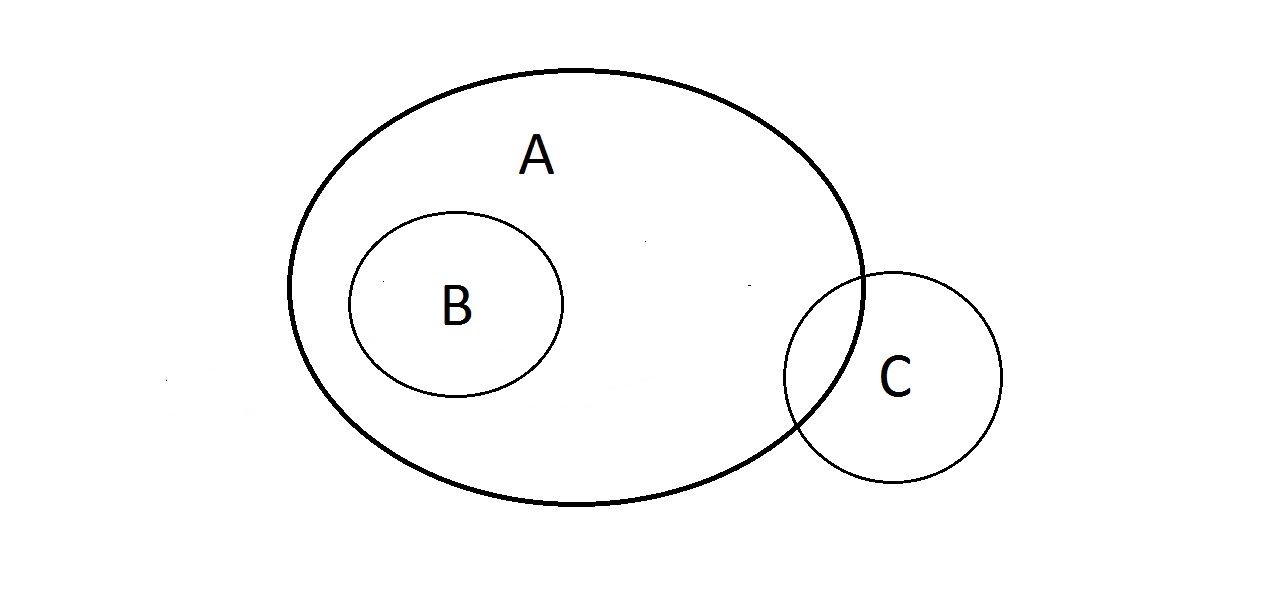
Wat kun je hiermee doen? De eigenschappen A en B zijn zoals hierboven, maar hoe zit het met C? Iets met eigenschap C kan in A liggen of misschien ook niet. Iets in A zou ook in C kunnen liggen of niet. Je kunt hier niets met C doen. We hebben wel de garantie dat iets dat B heeft, ook A heeft.

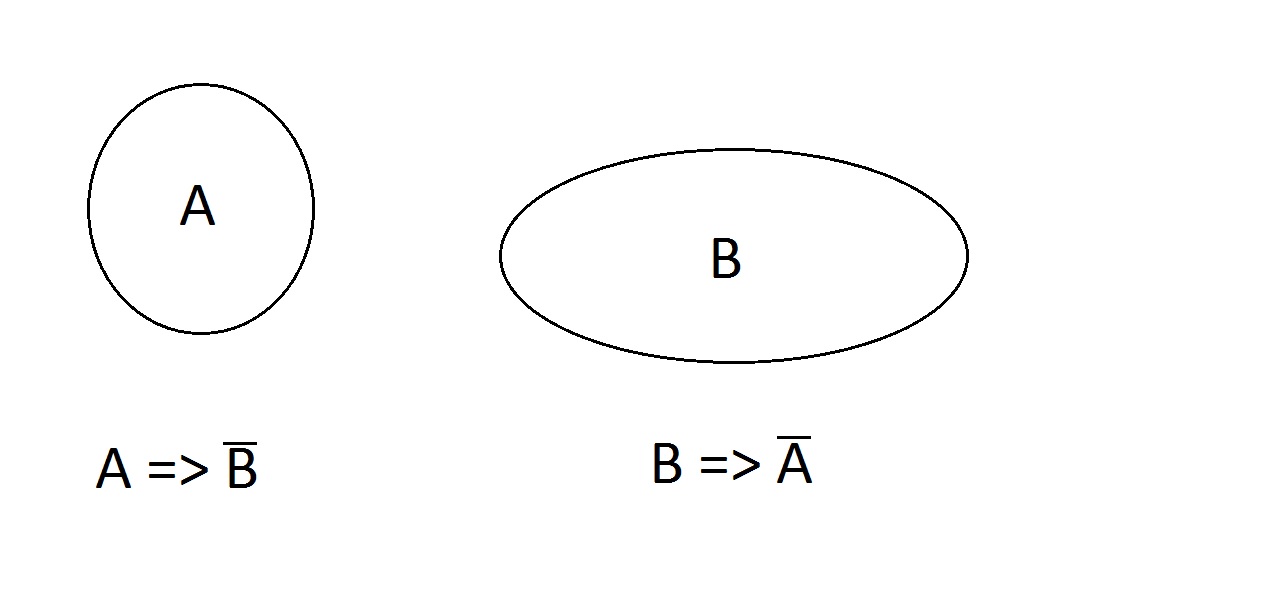
Hoe zit het dan. De eigenschappen zijn exclusief; een entiteit kan niet beide tegelijk hebben. Het kan geen, A, of B hebben, maar niet AB. De uitspraken A=> niet B en B => niet A zijn geldig.
Ten slotte willen we dat ons argument deugdelijk is. Om dit te bereiken, moet het argument een deductieve geldigheid hebben zoals hierboven beschreven en moeten de premissen waar zijn in de echte wereld. Dit betekent dat alle steekhoudende argumenten steekhoudend zijn, maar dat niet alle steekhoudende argumenten noodzakelijkerwijs steekhoudend zijn.

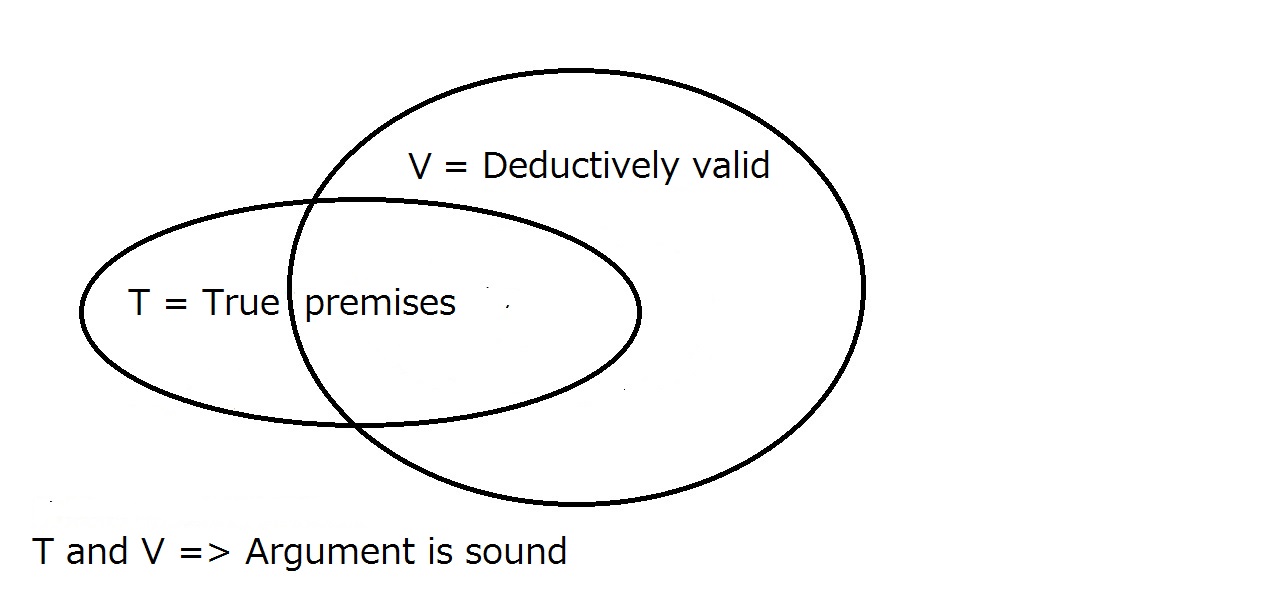
Een steekhoudend argument vereist dat het zowel steekhoudend is als dat de premissen waar zijn; het hebben van het ene garandeert niet automatisch het andere. Het gebied dat zich binnen zowel T als V bevindt, is het gebied van deugdelijke argumenten.

Dit is hoe ik het zie.

Aristoteles (384-322 BCE)

Van http://www.rwe.org/images/aristotle.jpgExperiment?
Zelf-consistent?
Als je theorie niet zelf-consistent is, of je theorie is het niet eens met zorgvuldige experimenten, dan is je theorie fout. Het maakt niet uit hoe mooi de theorie is; hij is fout.

Galileo Galilei (1564-1642)

Van http://helios.gsfc.nasa.gov/galileo.jpg

b.v. het vijfde postulaat van Euclides.

(1) Door twee verschillende punten is het mogelijk één lijn te trekken.
(2) Een eindige rechte lijn kan voortdurend in een rechte lijn worden verlengd.
(3) Een cirkel kan worden beschreven met elk punt als middelpunt en elke afstand als straal.
(4) Alle rechte hoeken zijn gelijk.
(5) Door een gegeven punt kan slechts één lijn evenwijdig aan een gegeven lijn worden getrokken.
De woorden “punt” en “lijn” hebben geen intrinsieke betekenis.
Je zou “punt” en “lijn” kunnen verwisselen en toch ware stellingen hebben.
Je zou kunnen zeggen
(1) Door twee verschillende blargs is het mogelijk één vloem te trekken…
Het vijfde postulaat kan op twee manieren worden veranderd:
(5) Door een gegeven punt kan geen lijn getrokken worden evenwijdig aan een gegeven lijn.
(5) Door een gegeven punt kunnen vele lijnen getrokken worden evenwijdig aan een gegeven lijn.
Beide van deze nieuwe postulaten geven aanleiding tot verschillende CONSISTENTe geometrieën.Welke is juist? Dat zijn ze allemaal! Welke beschrijft dit universum? Dat is FYSICA!