Apuntes del profesor Fisher sobre este tema en PDF
Presentaciones del profesor Fisher sobre este tema en PDF (requiere contraseña)
Presentaciones antiguas del profesor Sekula en PDF.

Inducción

Nota: Los filósofos (incluido el prof. Fisher) distinguen la inducción (generalización de los rasgos de alguna muestra a otras cosas) de la abducción (inferencia a la mejor explicación), mientras que el contenido que se presenta a continuación difumina ambas bajo el único título de «inducción». Al tomar esta clase con el profesor Fisher, es mejor confiar en sus apuntes o diapositivas sobre este tema, en lugar del contenido de abajo.

La inducción es un proceso de tratar de averiguar el funcionamiento de algún fenómeno mediante el estudio de una muestra del mismo. Se trabaja con una muestra porque no es posible estudiar todos los componentes del fenómeno.La inducción es un proceso creativo. El científico debe estudiar cuidadosamente una muestra de un fenómeno y, a continuación, formular una hipótesis para explicarlo.A continuación, se lleva a cabo el proceso científico de comprobación de la hipótesis.Los científicos que obtienen los resultados de investigación más espectaculares son los que son lo suficientemente creativos como para pensar en las preguntas de investigación adecuadas.

Las ciencias naturales (física, química, biología, etc.) son inductivas.Se recogen pruebas. Se aplica el Método Científico.Se parte de resultados concretos (una muestra) y se intenta adivinar las reglas generales. Las hipótesis sólo pueden refutarse, nunca probarse. Si una hipótesis resiste las pruebas repetidas de muchos investigadores independientes, aumenta la confianza en la hipótesis. Todas las hipótesis son tentativas; cualquiera podría ser derribada mañana, pero se requiere una evidencia muy fuerte para derribar una «Ley» o «Hecho».

Específica -> General

Aquí hay un ejemplo de inducción: Supongamos que he tomado 20 canicas al azar de una gran bolsa de canicas. Todas ellas han resultado ser blancas. Esa es mi observación: todas las canicas que he sacado eran blancas. Por tanto, podría formular la hipótesis de que esto se explicaría si todas las canicas de la bolsa fueran blancas. Podría ser que hubiera algunas canicas de distintos colores en la bolsa y que mi primera muestra simplemente no diera con ninguna.

Por cierto, este es un caso en el que podríamos demostrar que la hipótesis es verdadera.Podríamos simplemente tirar todas las canicas de la bolsa y examinar cada una de ellas.Este procedimiento se llama censo – mirar cada una. En la mayoría de los casos en los que se utiliza la inducción, el censo no es factible.

Abducción: Inferencia a la mejor explicación

Este es un método de razonamiento que no es riguroso como la Deducción.Suponga que tiene observaciones de un suceso interesante. No estás seguro inmediatamente de lo que explica las observaciones. Se trata de un proceso creativo, a diferencia de la deducción. Es un proceso creativo, a diferencia de la deducción. Para que funcione bien, hay que saber todo lo posible sobre la situación. Teniendo en cuenta todo lo que se sabe, se selecciona la hipótesis que parece más razonable y probable. Se ha elegido la mejor explicación aparente, aunque podría ser errónea. No hay ninguna garantía. Si es posible, es buena idea comprobar más a fondo tu explicación; podrías encontrar más información que te hiciera reconsiderar tu conclusión.

Este tipo de razonamiento es el fuerte de Sherlock Holmes. El famoso detective hiperobservador de Conan Doyle se da cuenta incluso de pistas muy pequeñas que el inspector de policía suele pasar por alto. Holmes combina estos indicios con los conocimientos generales que ha acumulado sobre el caso para dar con la mejor explicación: ¡el culpable! También explica cómo se cometió el crimen. En un bonito detalle para el lector, Holmes suele explicar el razonamiento que le llevó a la solución. Parece sencillo cuando Holmes lo explica…

Deducción

La matemática es una ciencia deductiva. Se proponen axiomas. No se ponen a prueba; se supone que son verdaderos. Los teoremas se deducen de los axiomas. Dados los axiomas y las reglas de la lógica, una máquina podríaproducir teoremas.

General -> Específica

Empezamos con la regla general y deducimos resultados específicos.Si el conjunto de axiomas produce un teorema y sunegación, el conjunto de axiomas se llama INCONSISTENTE.

Supongamos que tenemos las siguientes condiciones conocidas.

• Tenemos una gran bolsa de canicas.
• Se sabe que todas las canicas de la bolsa son blancas.
• Tengo una muestra aleatoria de 20 canicas tomadas de la bolsa.

A partir de ellas, puedo deducir que todas las canicas de la muestra son blancas, incluso sin mirarlas. Este tipo de razonamiento se llama modus ponens (más sobre esto a continuación y en las notas del profesor Fisher).

¿Qué tal esto?

• Tenemos una gran bolsa de canicas.
• Todas las canicas de la bolsa son blancas.
• Tengo una muestra de 20 canicas de colores mezclados.

De esto deduzco rápidamente que la muestra no fue tomada de la bolsa de canicas blancas. Este tipo de razonamiento se llama modus tollens (más sobre esto a continuación y en las notas del profesor Fisher).

Argumentos deductivos

Veamos la idea de razonamiento deductivo (derivada de las notas del profesor Fisher).Aquí estamos hablando de hacer un argumento para alguna idea o conclusión basada en un conjunto de premisas (hechos, ideas, etc).El profesor Fisher señala que los filósofos suelen mostrar esto como

1. Premise number 12. Premise number 2...------------------------C. Conclusion to be reached

Esta estructura constituye un argumento.A veces se escribe como
Premisa 1, Premisa 2, Premisa… => Conclusión.
Abreviemos esto en el silogismo así:
P => C (Las premisas implican la conclusión, igual que arriba)
Esto significa simplemente que si las premisas son verdaderas, entonces la conclusión también lo es.
«Para ser bueno, un argumento debe tener premisas verdaderas y las premisas deben ofrecer apoyo a la conclusión. El apoyo más fuerte posible proporcionaría una garantía absoluta de que la conclusión será verdadera (suponiendo, por supuesto, que las premisas sean verdaderas). Consideraremos primero ese tipo de apoyo, pero luego pasaremos a considerar también algunos tipos de apoyo más débiles.» (del profesor Fisher)
Un tipo de argumento especialmente útil es el argumento deductivamente válido. (Los argumentos deductivamente válidos son argumentos en los que las premisas, si son verdaderas, son la prueba más fuerte posible de que la conclusión es verdadera. De hecho, estos argumentos proporcionan la siguiente garantía: si las premisas son verdaderas, entonces la conclusión también debe serlo.
Un argumento que parece ser deductivo pero que tiene premisas que no apoyan la conclusión (no hay garantía) es un argumento inválido.
Repitamos el silogismo P => C (Las premisas llevan a la conclusión).Hay cuatro posibles afirmaciones que podrías hacer al respecto:

1. Todas las premisas son verdaderas (P es verdadera) (razonamiento modus ponens)
2. Una o más de las premisas es falsa (P es falsa – no P)
3. La conclusión es verdadera (C es verdadera)
4. La conclusión es falsa (C es falsa – no C) (razonamiento modus tollens)

Sólo dos de ellos (#1 y #4) constituyen un razonamiento deductivamente válido.Veamos la razón de esto, una elección a la vez.

1. P es verdadero (P) – Afirmación del antecedente. Si todas las premisas son verdaderasla conclusión debe ser verdadera. Este es un argumento muy fuerte. (modus ponens)
2. P es falso (no P) – Negando el antecedente. Que P sea falso no garantiza que C sea verdadero o falso. Podría haber otras causas.
3. C es verdadero (C) – Afirmar el consecuente. Si C es verdadero podría ser por una de varias razones, no esta P específica.
4. C es falso (no C) – Negando el consecuente. Aquí, si C es falso entoncesP también debe ser falso. Si P fuera verdadero C también lo sería. (modus tollens)

En resumen, #1 y #4 (modus ponens y modus tollens) son deductivamente válidos mientras que #2 y #3 no lo son.
Si las premisas se aplican a cosas en el mundo real, todavía hay que hacer una prueba de invalidez. Hay al menos tres enfoques.

1. A ver si puedes encontrar un escenario en el que las premisas sean verdaderas pero la conclusión sea falsa.
2. Intenta reemplazar un sustantivo o adjetivo del argumento por otro.Reemplaza todos los casos. Si es obvio que no es válido, entonces el original no era válido.
3. Representa P y C en un diagrama de Venn.Si puedes hacerlo de forma que P sea verdadera pero C sea falsa, el argumento no es válido. Hemos hecho estos diagramas para usted a continuación.

Ahora traemos el tema de los diagramas de Venn. Estos pueden ser de gran valor para comprobar las premisas de un argumento.

Diagramas de Venn

Los diagramas de Venn son un método gráfico de representación de la lógica.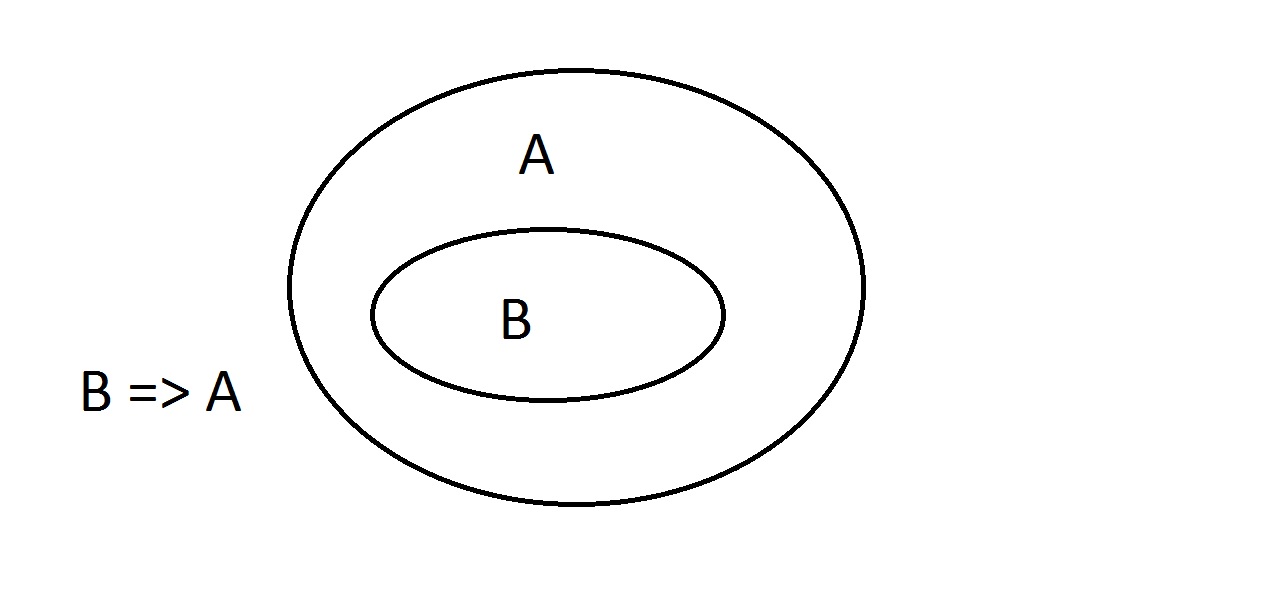
Este es el diagrama más simple que tendrás. El óvalo exterior contiene todas las cosas que tienen la propiedad A, mientras que el óvalo interior contiene todas las cosas que tienen la propiedad B, así como la propiedad A.Esto se muestra como B=>A, lo que significa que todas las cosas que tienen la propiedad B también tienen la propiedad A.También se podría decir «B implica A». Esta es la garantía mencionada anteriormente.
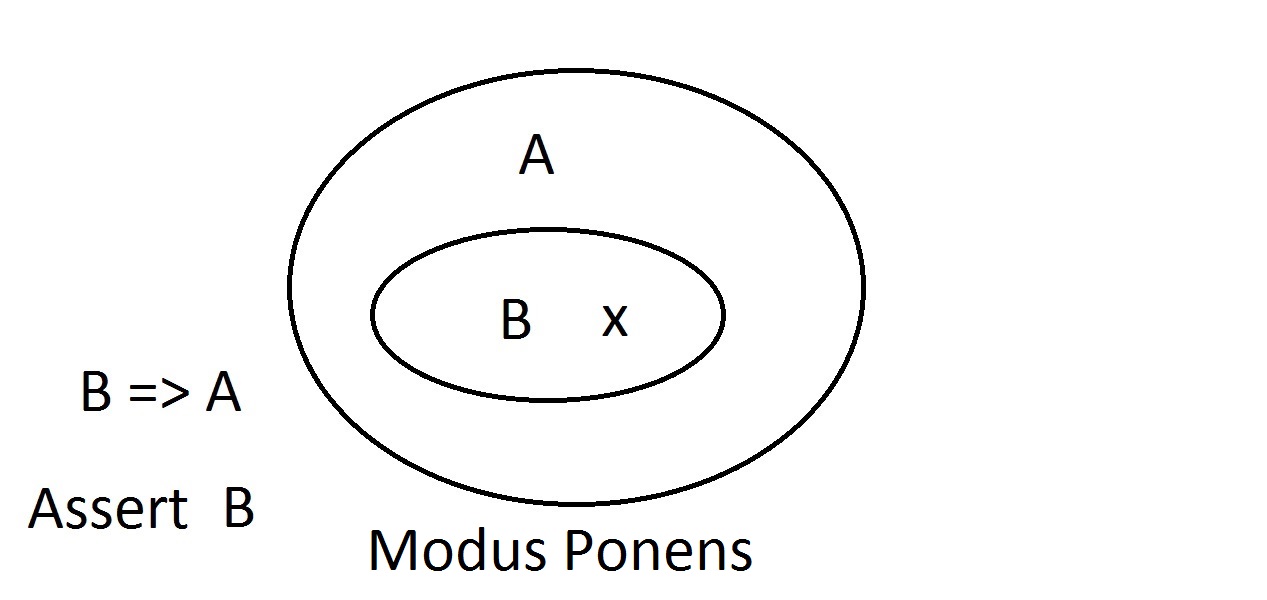Aseguraremos ahora que tenemos algo con la propiedad B. Podemos afirmar con seguridad que también tiene la propiedad A. Esto es un razonamiento de Modus Ponens (afirmación del antecedente). Cualquier entidad con la propiedad B obviamente debe estar también en el espacio de la propiedad A.
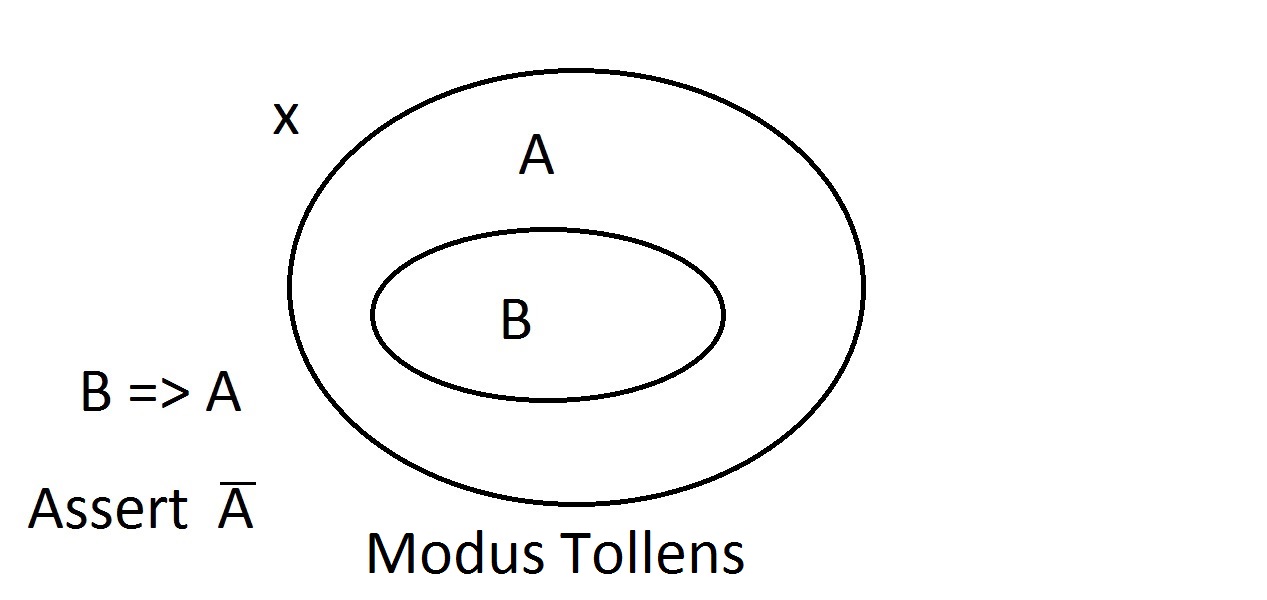Supongamos ahora que una entidad no tiene la propiedad A. El diagrama de Venn muestra que tampoco puede tener la propiedad B. Todo lo que esté fuera del espacio de la propiedad A debe estar también fuera del espacio de la propiedad B. Esto es un razonamiento de Modus Tollens (negación del consecuente) y es válido y fuerte.
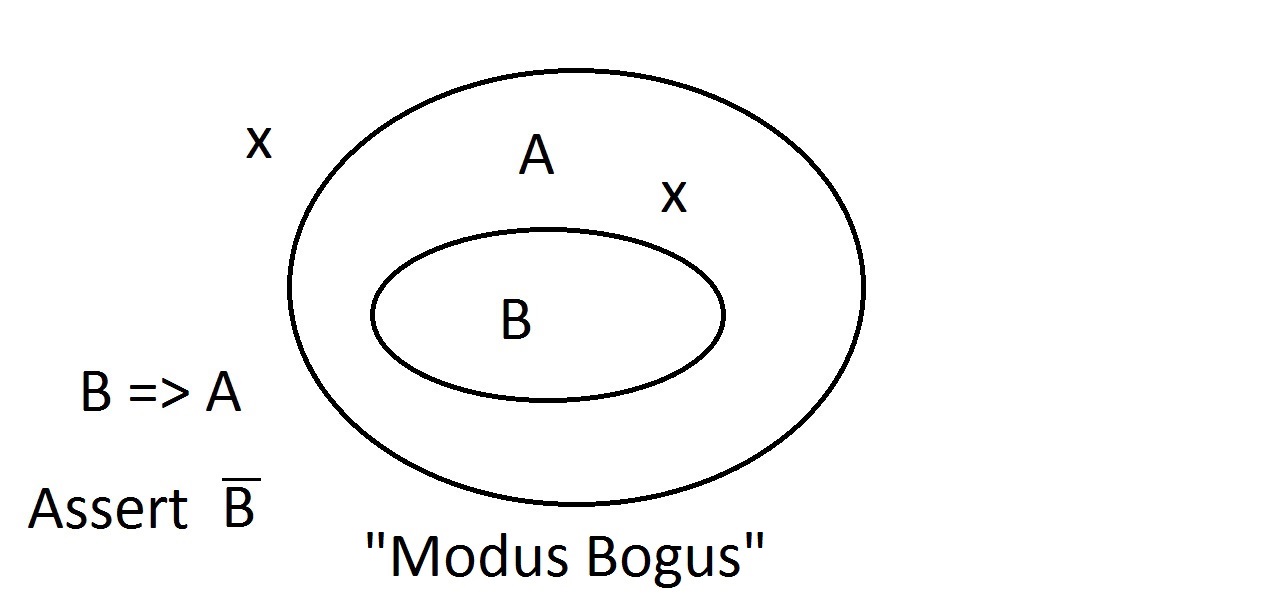Ahora intentaremos afirmar que nuestra cosa no posee la propiedad B. Un vistazo al diagrama deVenn muestra el problema aquí. Una entidad que no tiene la propiedad B puede estar dentro del espacio A o fuera de él. La afirmación de «no B» no nos dice nada sobre A. Esto no es un razonamiento válido, por lo que lo llamamos Modus Bogus. Es negar el antecedente y no es válido.
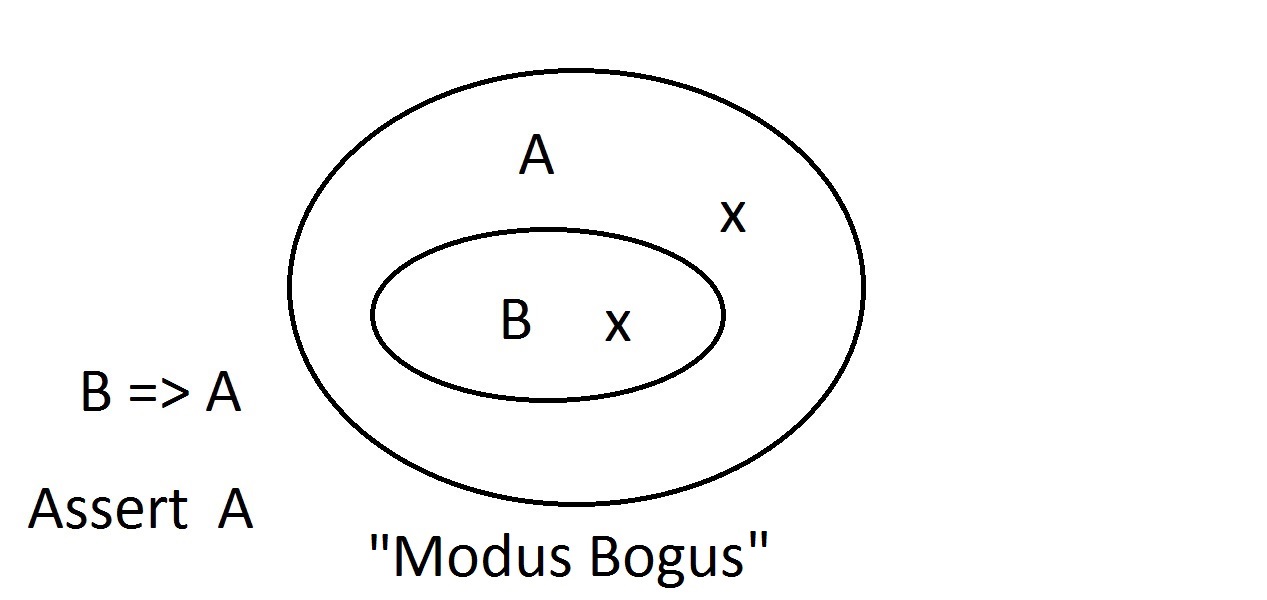La última posibilidad es afirmar que nuestra cosa tiene la propiedad A.El diagrama de Venn muestra el problema. La entidad podría estar en cualquier lugar del espacio A, ya sea dentro o fuera del espacio B. Afirmar que la cosa tiene la propiedad A no te dice nada sobre si también tiene B. Esto también es Modus Bogus, o razonamiento inválido.Se llama Afirmar el Consecuente.
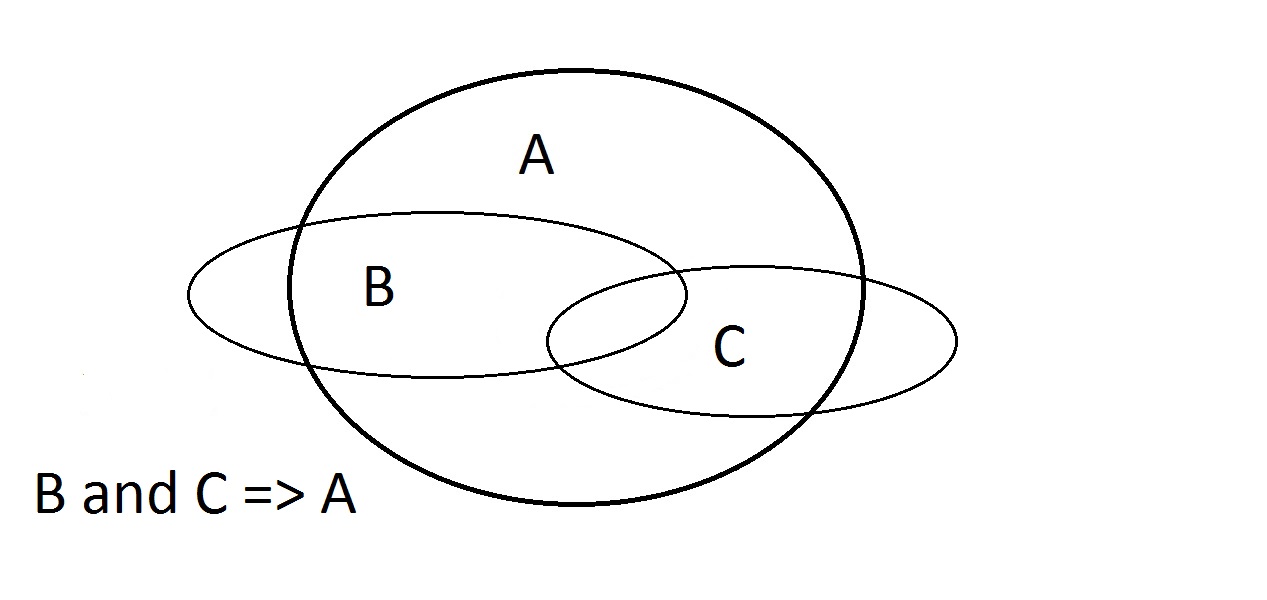Aquí estamos tratando con las propiedades A, B y C.Aquí podemos garantizar sólo que una entidad que tiene B y C también tiene A.Observa que algunos de los espacios B y C se encuentran fuera de A.

• Asegurar A: Podría estar en cualquier parte de A
• Asegurar B: Algo de B queda fuera de A
• Asegurar C: Algo de C queda fuera de A
• Asegurar A y B: Podría incluir algo de C; podría no.
• Asegurar B y C: La intersección BC está enteramente en A. Argumentar que B y C => A funciona.
• Asegurar A y C: Podría incluir algo de B; podría no

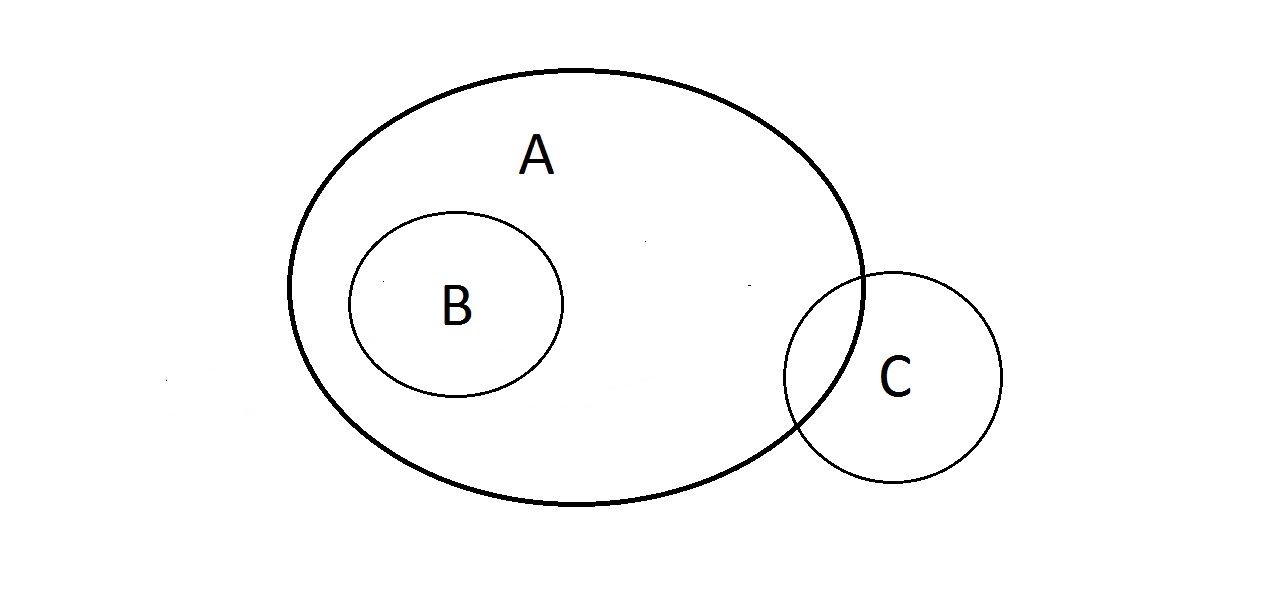
¿Qué puedes hacer con esto? Las propiedades A y B son como las anteriores, pero ¿qué pasa con C? Algo que tiene la propiedad C puede estar dentro de A o no. Algo que está en A puede estar también en C o no. Aquí no se puede hacer nada con C. Tenemos la garantía de que algo que tiene B también tiene A.

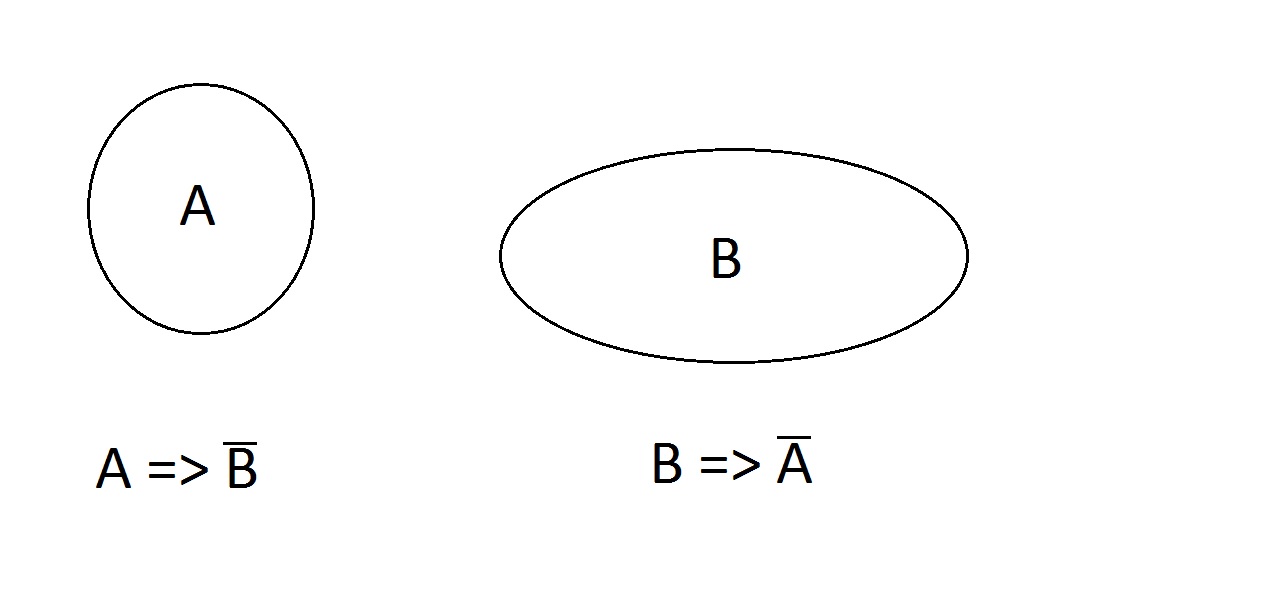
Qué tal esto. Las propiedades son excluyentes; una entidad no puede tener ambas al mismo tiempo.Puede no tener ninguna, A, o B pero no AB. Las afirmaciones A=> no B y B => no A son válidas.
Por último, queremos que nuestro argumento sea sólido. Para que esto ocurra, el argumento debe ser deductivamente válido como se ha dicho anteriormente y las premisas deben ser verdaderas en el mundo real. Esto significa que todos los argumentos sólidos son válidos, pero que todos los argumentos válidos no son necesariamente sólidos.

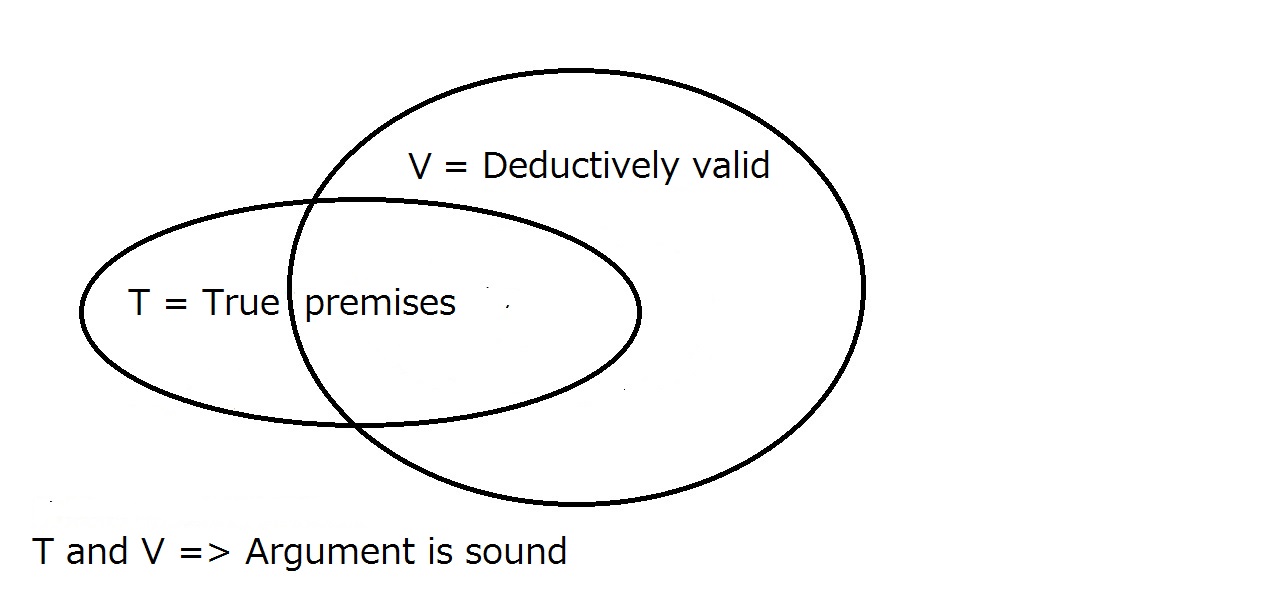
Un argumento sólido requiere que sea deductivamente válido y que tenga premisas verdaderas. La región que está dentro tanto deT como de V es la región de los argumentos sólidos.

Así es como yo lo veo. Escuchadme todos.

Aristóteles (384-322 a.C.)

¿De http://www.rwe.org/images/aristotle.jpgExperiment?
Autoconsistente?
Si tu teoría no es autoconsistente, o tu teoría no está de acuerdo con los experimentos cuidadosos, entonces tu teoría es errónea. No importa lo hermosa que sea la teoría; está equivocada.

Galileo Galilei (1564-1642)

De http://helios.gsfc.nasa.gov/galileo.jpg

por ejemplo, el quinto postulado de Euclides.

(1) A través de dos puntos diferentes cualesquiera, es posible trazar una línea.
(2) Una recta finita puede prolongarse continuamente en línea recta.
(3) Una circunferencia puede describirse con cualquier punto como centro y cualquier distancia como radio.
(4) Todos los ángulos rectos son iguales.
(5) A través de un punto dado, sólo puede trazarse una línea paralela a una recta dada.
Las palabras «punto» y «recta» no tienen ningún significado intrínseco.
Se podrían intercambiar «punto» y «recta» y seguirían teniendo teoremas verdaderos.
Se podría decir
(1) A través de dos blargs diferentes cualesquiera, es posible trazar una fle…
El quinto postulado se puede cambiar de dos maneras:
(5) A través de un punto dado, no se puede dibujar ninguna línea paralela a una línea dada.
(5) A través de un punto dado, se pueden dibujar muchas líneas paralelas a una línea dada.
Ambos postulados nuevos dan lugar a geometrías CONSISTENTES diferentes.¿Cuál es el correcto? Todas lo son. ¿Cuál describe este Universo? Eso es la FÍSICA.