Appunti del Professor Fisher su questo argomento in PDF
Diapositive del Professor Fisher su questo argomento in PDF (richiesta password)
Vecchie diapositive del Professor Sekula in PDF.

Induzione

Nota: I filosofi (incluso il prof. Fisher) distinguono l’induzione (generalizzare le caratteristiche di un certo campione ad altre cose) dall’abduzione (inferenza alla migliore spiegazione), mentre il contenuto qui sotto li confonde entrambi insieme sotto l’unico titolo di “induzione”. Quando si segue questo corso con il Professor Fisher, è meglio affidarsi ai suoi appunti o alle diapositive su questo argomento, piuttosto che al contenuto sottostante.

L’induzione è un processo che cerca di capire il funzionamento di un fenomeno studiandone un campione. Si lavora con un campione perché guardare ogni componente del fenomeno non è fattibile.L’induzione è un processo creativo. Lo scienziato deve studiare attentamente un campione di un fenomeno, quindi formulare un’ipotesi per spiegare il fenomeno.Segue il processo scientifico di verifica dell’ipotesi.Gli scienziati che ottengono i risultati di ricerca più spettacolari sono quelli che sono abbastanza creativi da pensare alle domande di ricerca giuste.

Le scienze naturali (fisica, chimica, biologia, ecc.) sono induttive.Si raccolgono prove. Si applica il metodo scientifico, si parte da risultati specifici (un campione) e si cerca di indovinare le regole generali. Le ipotesi possono essere solo confutate, mai dimostrate. Se un’ipotesi resiste a prove ripetute da molti ricercatori indipendenti, allora la fiducia cresce nell’ipotesi. Tutte le ipotesi sono provvisorie; ognuna potrebbe essere ribaltata domani, ma sono necessarie prove molto forti per rovesciare una “Legge” o un “Fatto”.

Specifico -> Generale

Ecco un esempio di induzione: Supponiamo che io abbia preso 20 biglie a caso da un grande sacchetto di biglie. Ognuna di esse è risultata essere bianca. Questa è la mia osservazione – ogni biglia che ho preso era bianca. Potrei quindi formulare l’ipotesi che questo si spiegherebbe se tutte le biglie nel sacchetto fossero bianche. Un ulteriore campionamento sarebbe necessario per testare l’ipotesi.Potrebbe essere che ci sono alcune biglie di vari colori nel sacchetto e il mio primo campione semplicemente non ne ha colpita nessuna.

Incidentalmente, questo è un caso in cui potremmo provare che l’ipotesi è vera.Potremmo semplicemente buttare fuori tutte le biglie nel sacchetto ed esaminare ognuna di esse.Tale procedura è chiamata un censimento – guarda ogni biglia. Nella maggior parte dei casi in cui si usa l’induzione un censimento non è fattibile.

Abduzione: Inferenza alla migliore spiegazione

Questo è un metodo di ragionamento che non è rigoroso come la deduzione. Non siete immediatamente sicuri di cosa spieghi le osservazioni. Si pensa a tutte le ipotesi possibili che potrebbero spiegare plausibilmente le osservazioni. Questo è un processo creativo, a differenza della deduzione. Per far sì che funzioni bene, è necessario sapere quanto più possibile sulla situazione. Dato tutto quello che si sa, si sceglie l’ipotesi che appare più ragionevole e probabile: si è scelta la spiegazione apparentemente migliore, anche se potrebbe essere sbagliata, non ci sono garanzie. Un ulteriore controllo della tua spiegazione è solitamente una buona idea, se è possibile; potresti trovare altre informazioni che potrebbero farti riconsiderare la tua conclusione.

Questo tipo di ragionamento è il forte di Sherlock Holmes. Il detective di Conan Doyle, notoriamente iper-osservatore, si accorge di indizi anche molto piccoli che di solito sfuggono all’ispettore di polizia. Holmes combina questi indizi con la conoscenza generale che ha accumulato sul caso per arrivare alla migliore spiegazione – whodunit! Spiega anche come è stato commesso il crimine. In un bel tocco per il lettore, Holmes spiega spesso il ragionamento che lo ha portato alla soluzione. Sembra semplice quando Holmes lo spiega…

Deduzione

La matematica è una scienza deduttiva. Si propongono assiomi. Non vengono testati; si assume che siano veri. I teoremi sono dedotti dagli assiomi. Dati gli assiomi e le regole della logica, una macchina potrebbe produrre teoremi.

Generale -> Specifico

Partiamo dalla regola generale e deduciamo risultati specifici.Se l’insieme degli assiomi produce un teorema e la sua negazione, l’insieme degli assiomi è detto INCONSISTENTE.

Supponiamo di avere le seguenti condizioni note.

• Abbiamo un grande sacchetto di biglie.
• Tutte le biglie del sacchetto sono note per essere bianche.
• Ho un campione casuale di 20 biglie prese dal sacchetto.

Da queste, posso dedurre che tutte le biglie del campione sono bianche, anche senza guardarle. Questo tipo di ragionamento si chiama modus ponens (maggiori informazioni in seguito e negli appunti del Prof. Fisher).

Che ne dite di questo?

• Abbiamo un grande sacchetto di biglie.
• Tutte le biglie nel sacchetto sono bianche.
• Ho un campione di 20 biglie di colori misti.

Da questo deduco rapidamente che il campione non è stato preso dal sacchetto delle biglie bianche. Questo tipo di ragionamento è chiamato modus tollens (maggiori informazioni in seguito e negli appunti del Prof. Fisher).

Aiuti deduttivi

Guardiamo l’idea di ragionamento deduttivo (derivato dagli appunti del Prof. Fisher).Qui stiamo parlando di fare un’argomentazione per qualche idea o conclusione basata su un insieme di premesse (fatti, idee, ecc.). Il Prof. Fisher nota che i filosofi di solito mostrano questo come

1. Premise number 12. Premise number 2...------------------------C. Conclusion to be reached

Questa struttura costituisce un argomento.A volte viene scritto come
Premessa 1, Premessa 2, Premessa… => Conclusione.
Abbreviamo questo nel sillogismo in questo modo:
P => C (Le premesse implicano la conclusione, proprio come sopra)
Questo significa semplicemente che se le premesse sono vere, allora anche la conclusione è vera.
“Per essere buono, un argomento deve avere premesse vere e le premesse devono offrire supporto alla conclusione. Il supporto più forte possibile fornirebbe una garanzia assoluta che la conclusione sarà vera (presumendo, naturalmente, che le premesse siano vere). Considereremo prima questo tipo di supporto, ma poi passeremo a considerare anche alcuni tipi di supporto più deboli”. (dal Prof. Fisher)
Un tipo di argomento particolarmente utile è un argomento deduttivamente valido. (Questo è spesso abbreviato come “argomento valido” o talvolta come “argomento deduttivo”). Gli argomenti deduttivamente validi sono argomenti in cui le premesse, se vere, sarebbero la prova più forte possibile che la conclusione è vera. Infatti questi argomenti forniscono la seguente garanzia: se le premesse sono vere, allora anche la conclusione deve essere vera.
Un argomento che sembra essere deduttivo ma ha premesse che non sostengono la conclusione (nessuna garanzia) è un argomento non valido.
Ripetiamo il sillogismo P => C (Le premesse portano alla conclusione).Ci sono quattro possibili affermazioni che si possono fare su questo:

1. Tutte le premesse sono vere (P è vero) (ragionamento modus ponens)
2. Una o più delle premesse è falsa (P è falso – non P)
3. La conclusione è vera (C è vero)
4. La conclusione è falsa (C è falso – non C) (ragionamento modus tollens)

Solo due di queste (#1 e #4) costituiscono un ragionamento deduttivamente valido.Vediamo la ragione di questo, una scelta alla volta.

1. P è vero (P) – Affermando l’antecedente. Se tutte le premesse sono vere, la conclusione deve essere vera. Questo è un argomento molto forte. (modus ponens)
2. P è falso (non P) – Negare l’antecedente. Il fatto che P sia falso non garantisce che C sia vero o falso. Ci potrebbero essere altre cause.
3. C è vero (C) – Affermare il conseguente. Se C è vero potrebbe essere per una delle tante ragioni, non per questa specifica P.
4. C è falso (non C) – Negare il conseguente. Qui, se C è falso allora anche P deve essere falso. Se P fosse vero, lo sarebbe anche C. (modus tollens)

In breve, #1 e #4 (modus ponens e modus tollens) sono deduttivamente validi mentre #2 e #3 non lo sono.
Se le premesse si applicano a cose del mondo reale, è ancora necessario fare un test di invalidità. Ci sono almeno tre approcci.

1. Vedi se riesci a trovare uno scenario in cui le premesse sono vere ma la conclusione è falsa.
2. Prova a sostituire un nome o un aggettivo nell’argomento con un altro. Se questo ovviamente non è valido, allora l’originale non era valido.
3. Rappresenta P e C in un diagramma di Venn.Se puoi farlo in modo che P sia vero ma C sia falso, l’argomento non è valido. Abbiamo fatto questi diagrammi per voi qui sotto.

Ora tiriamo fuori l’argomento dei diagrammi di Venn. Questi possono essere di grande valore per controllare le premesse di un argomento.

Diagrammi di Venn

I diagrammi di Venn sono un metodo grafico per rappresentare la logica.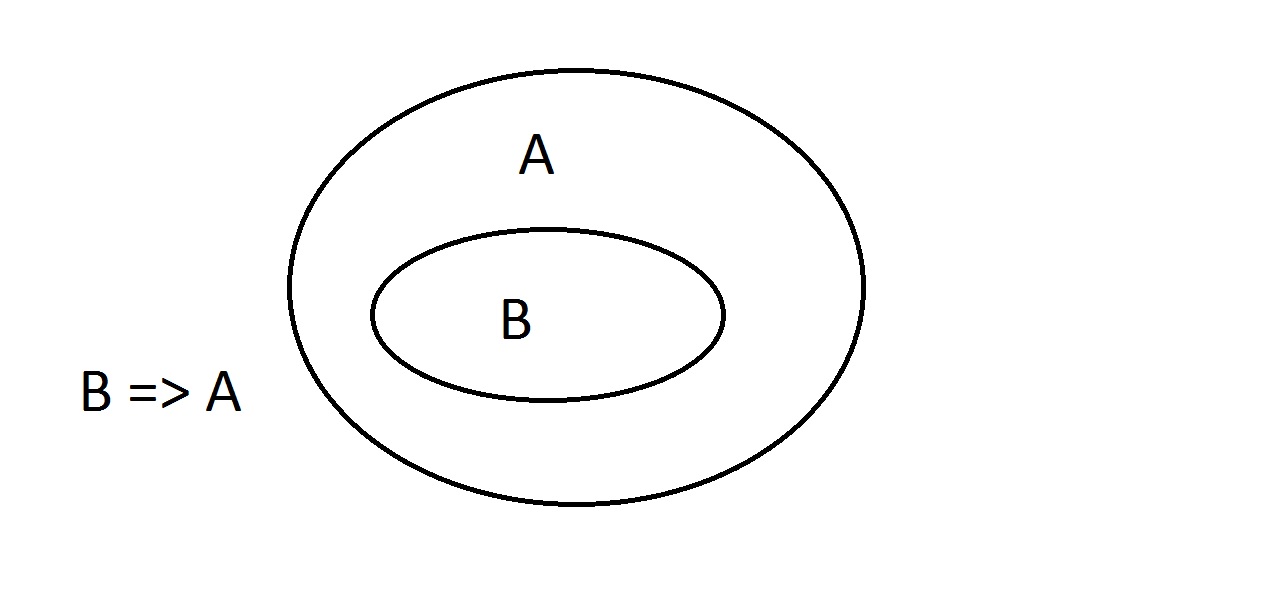
Questo è il diagramma più semplice che avrete. L’ovale esterno contiene tutte le cose che hanno la proprietà A, mentre l’ovale interno contiene tutte le cose che hanno la proprietà B e la proprietà A. Questo è mostrato come B=>A, il che significa che tutte le cose che hanno la proprietà B hanno anche la proprietà A. Si potrebbe anche dire “B implica A.” Se B è vero, allora anche A deve esserlo. Questa è la garanzia menzionata sopra.
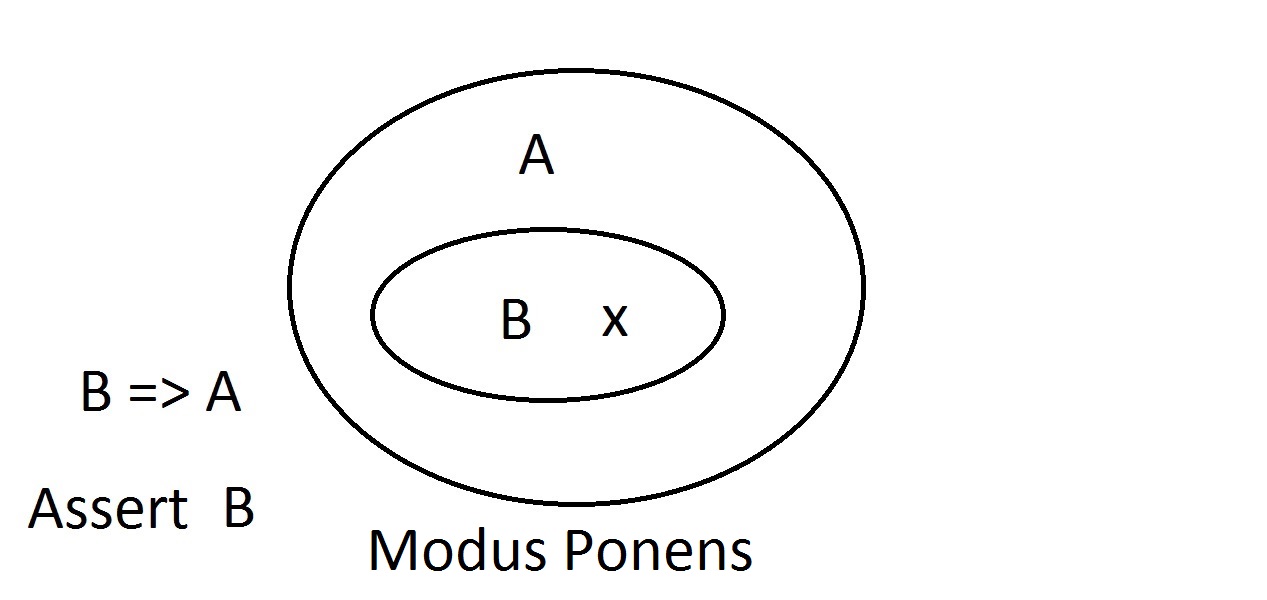Asseriamo ora che abbiamo qualcosa con proprietà B. Possiamo affermare con sicurezza che ha anche la proprietà A. Questo è un ragionamento Modus Ponens (affermare l’antecedente). Qualsiasi entità con la proprietà B deve ovviamente essere anche nello spazio della proprietà A.
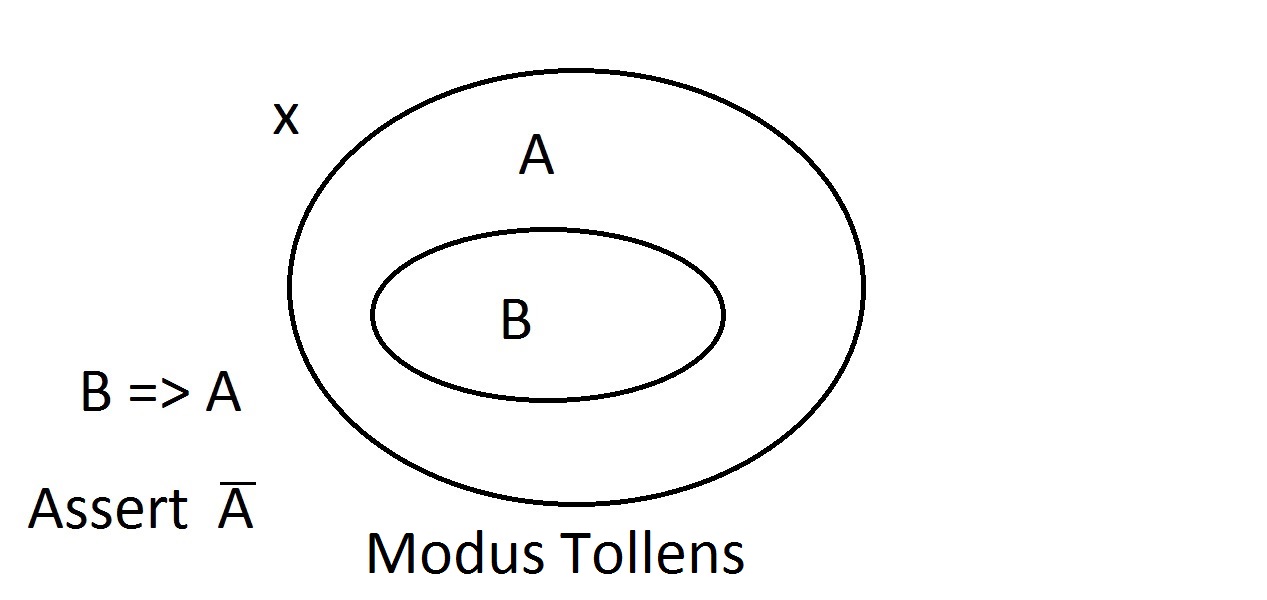Supponiamo ora di affermare che un’entità non abbia la proprietà A. Il diagramma di Venn mostra che non può avere neanche la proprietà B. Qualsiasi cosa fuori dallo spazio della proprietà A deve essere anche fuori dallo spazio della proprietà B. Questo è un ragionamento Modus Tollens (che nega il conseguente) ed è valido e forte.
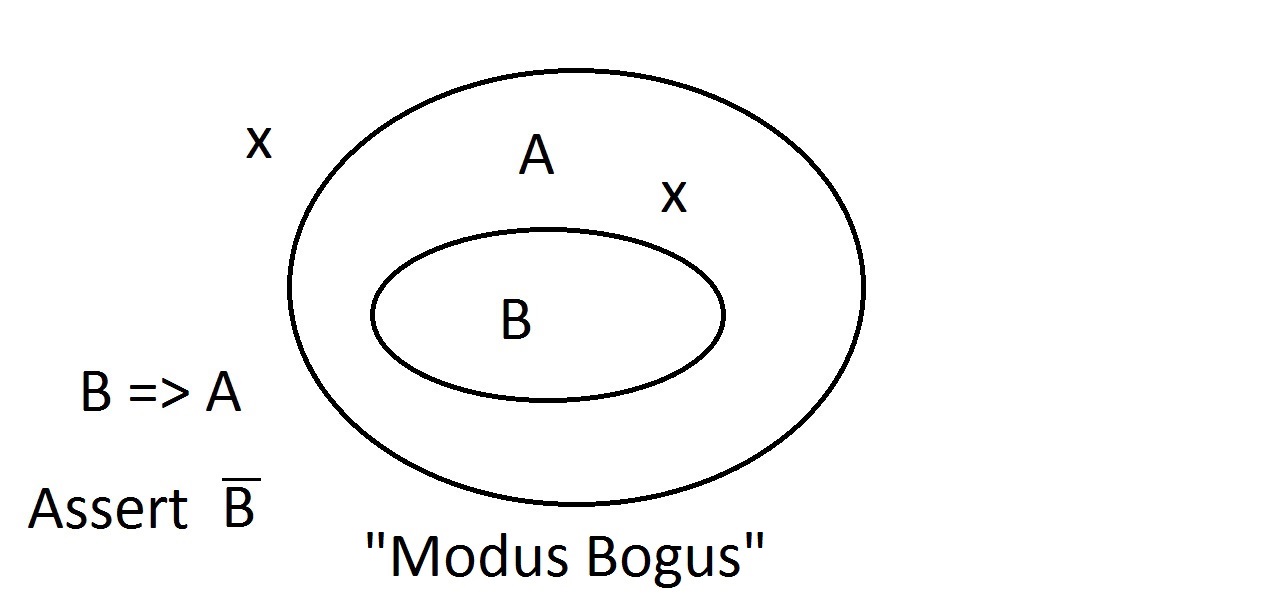Ora proviamo ad affermare che la nostra cosa non possiede la proprietà B. Uno sguardo al diagramma di Venn mostra il problema qui. Un’entità che non possiede la proprietà B può trovarsi all’interno dello spazio A o al di fuori di esso. L’affermazione “non B” non ci dice nulla su A. Questo non è un ragionamento valido, quindi lo abbiamo chiamato Modus Bogus. È negare l’antecedente e non è valido.
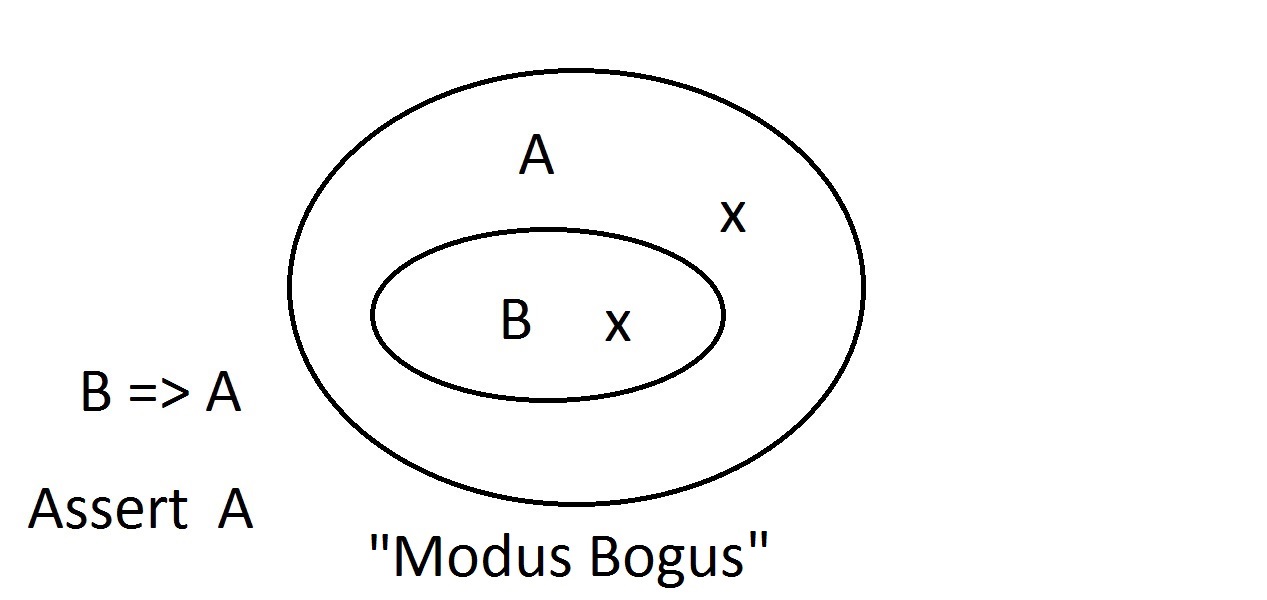L’ultima possibilità è affermare che la nostra cosa ha la proprietà A. Il diagramma di Venn mostra il problema. L’entità potrebbe trovarsi ovunque nello spazio A, sia dentro che fuori lo spazio B. Affermare che la cosa ha la proprietà A non vi dice nulla sul fatto che abbia anche B. Questo è anche Modus Bogus, o ragionamento non valido.Si chiama Affermare il Conseguente.
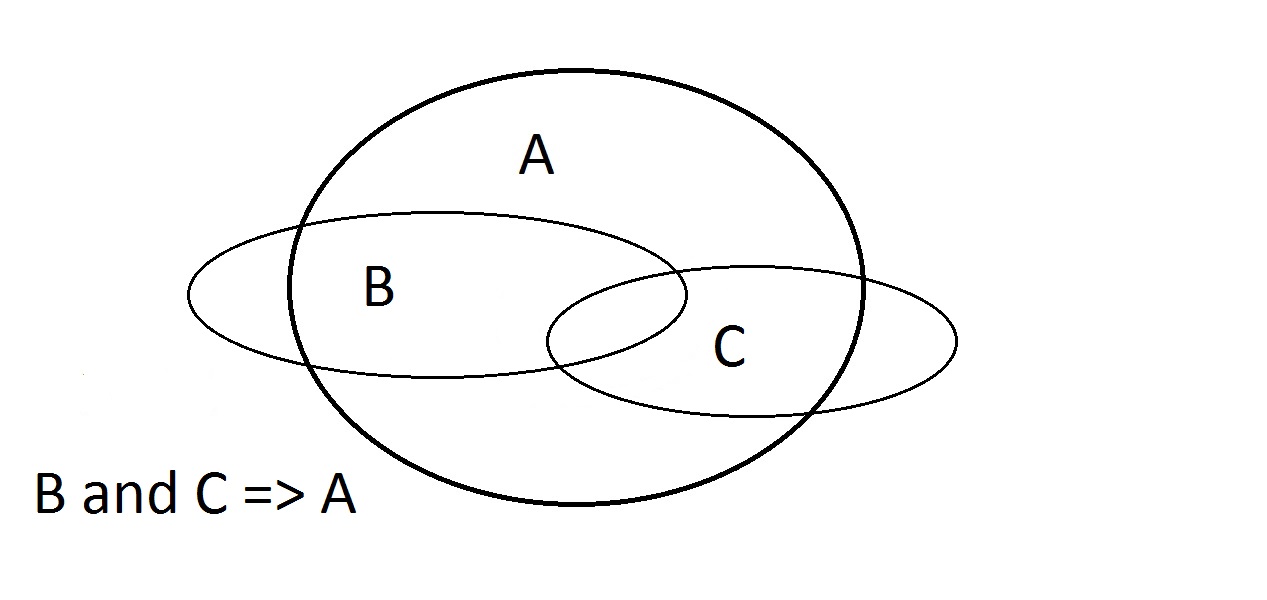Qui abbiamo a che fare con le proprietà A, B e C.Qui possiamo garantire solo che un’entità che ha B e C ha anche A.Notate che alcuni degli spazi B e C sono fuori da A.

• Asserisci A: Potrebbe essere ovunque in A
• Asserisci B: Una parte di B si trova fuori da A
• Asserisci C: Una parte di C si trova fuori da A
• Asserisci A e B: Potrebbe includere qualche C; potrebbe non farlo.
• Asserisci B e C: L’intersezione BC si trova interamente in A. Sostenere che B e C => A funziona.
• Asserisci A e C: Potrebbe includere alcuni B; potrebbe non farlo

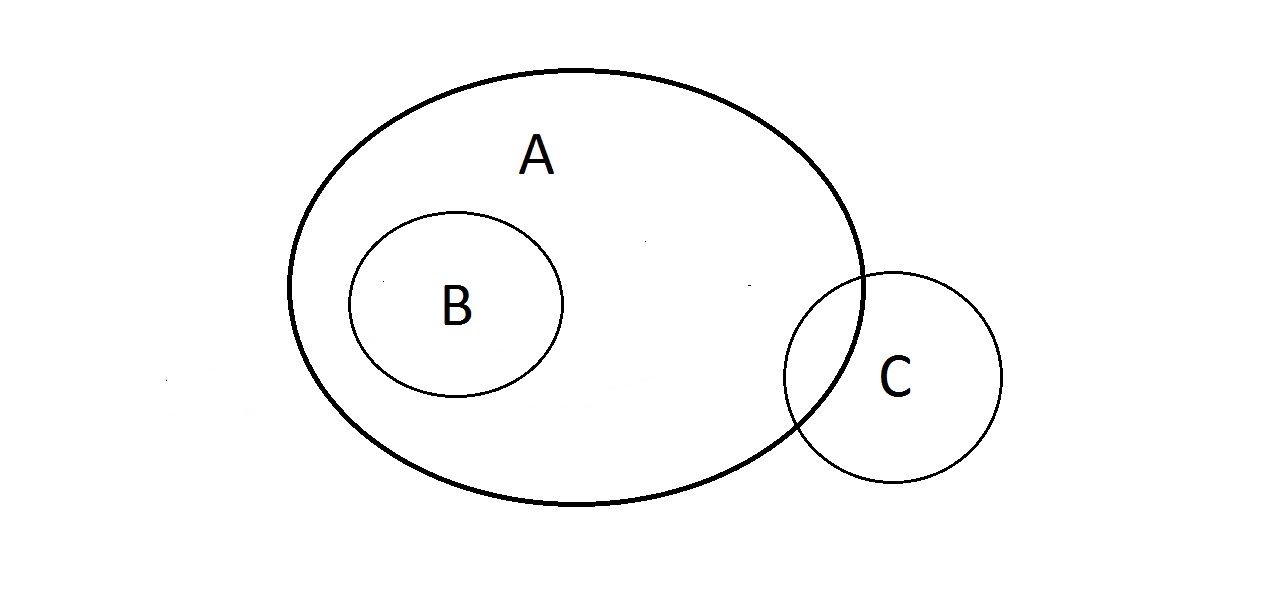
Cosa puoi fare con questo? Le proprietà A e B sono come sopra, ma che dire di C? Qualcosa che ha la proprietà C potrebbe trovarsi all’interno di A oppure no. Qualcosa in A potrebbe anche essere in C oppure no. Qui non si può fare nulla con C. Abbiamo la garanzia che qualcosa che ha B ha anche A.

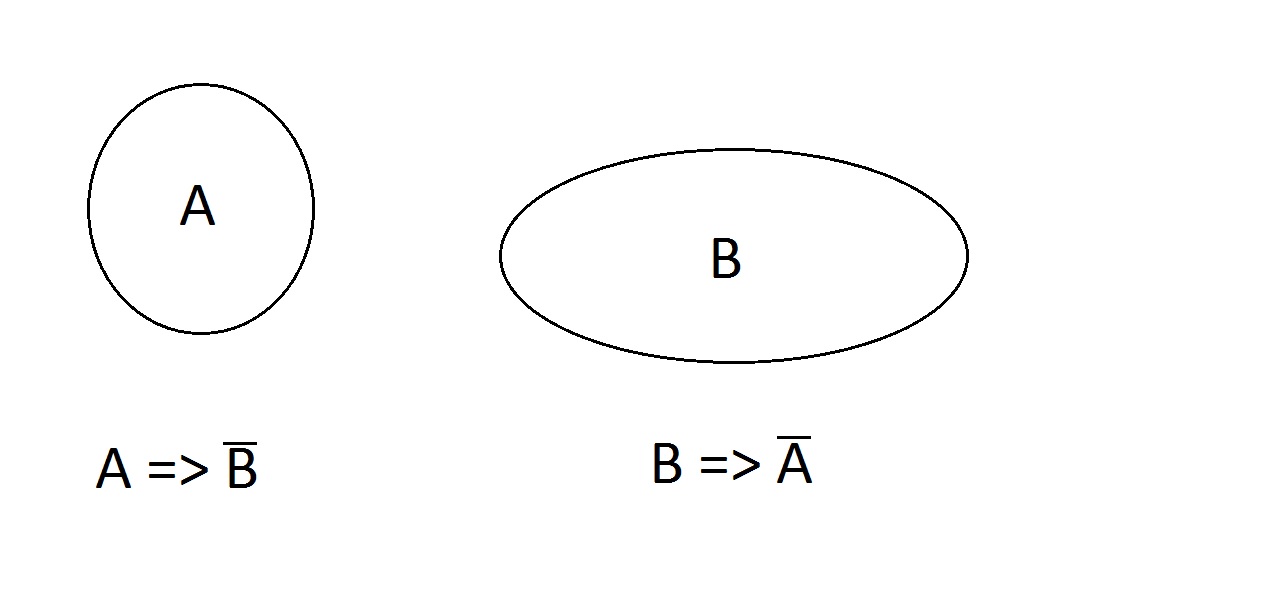
Come questo. Le proprietà sono esclusive; un’entità non può averle entrambe allo stesso tempo; può non averne nessuna, A, o B ma non AB. Le affermazioni A=> non B e B => non A sono valide.
Infine, vogliamo che il nostro argomento sia valido. Perché questo accada, l’argomento deve essere deduttivamente valido come sopra e le premesse devono essere vere nel mondo reale. Questo significa che tutti gli argomenti validi sono validi, ma tutti gli argomenti validi non sono necessariamente validi.

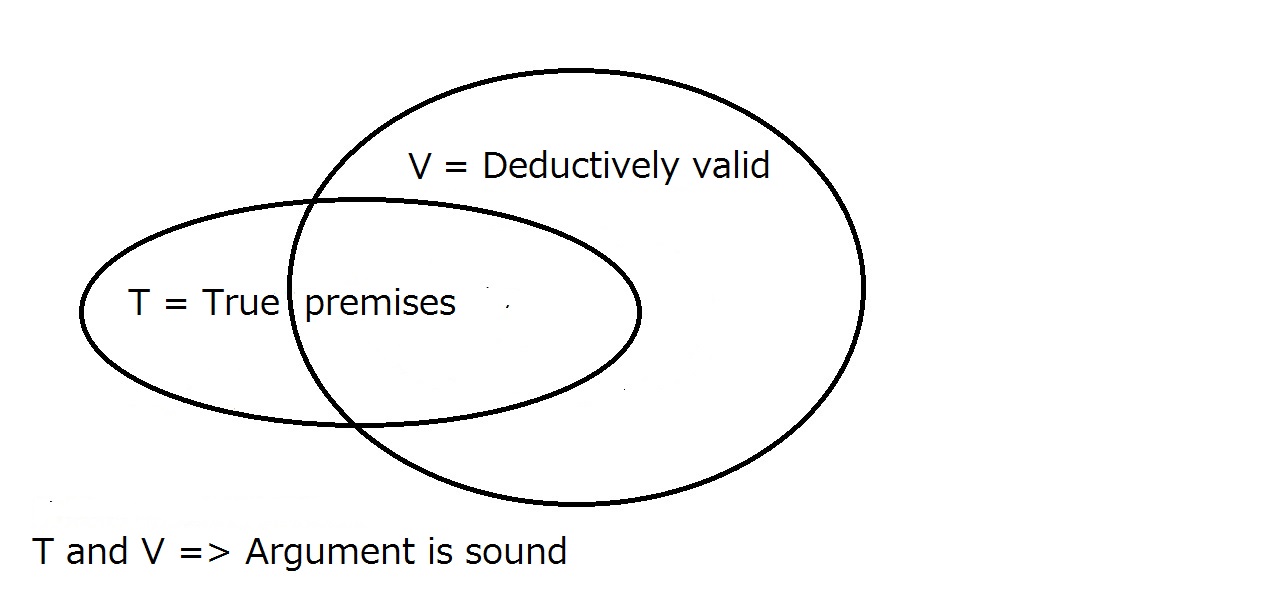
Un argomento valido richiede che sia deduttivamente valido e che abbia premesse vere; avere l’uno non garantisce automaticamente l’altro. La regione che si trova all’interno sia di T che di V è la regione degli argomenti validi.

Ecco come la vedo io. Ascoltatemi tutti.

Aristotele (384-322 a.C.)

Da http://www.rwe.org/images/aristotle.jpgExperiment?
Autoconsistente?
Se la tua teoria non è autoconsistente, o la tua teoria non è in accordo con esperimenti accurati, allora la tua teoria è sbagliata. Non importa quanto sia bella la teoria: è sbagliata.

Galileo Galilei (1564-1642)

Da http://helios.gsfc.nasa.gov/galileo.jpg

per esempio il quinto postulato di Euclide.

(1) Attraverso due punti diversi è possibile tracciare una linea.
(2) Una linea retta finita può essere estesa continuamente in una linea retta.
(3) Un cerchio può essere descritto con qualsiasi punto come centro e qualsiasi distanza come raggio.
(4) Tutti gli angoli retti sono uguali.
(5) Attraverso un dato punto, solo una linea può essere disegnata parallela ad una data linea.
Le parole “punto” e “linea” non hanno alcun significato intrinseco.
Si potrebbe scambiare “punto” e “linea” e avere ancora dei teoremi veri.
Si potrebbe dire
(1) Attraverso due barbi differenti qualsiasi, è possibile disegnare una linea…
Il quinto postulato può essere cambiato in due modi:
(5) Attraverso un punto dato, nessuna linea può essere disegnata parallela ad una linea data.
(5) Attraverso un punto dato, molte linee possono essere disegnate parallelamente ad una linea data.
Entrambi questi nuovi postulati danno origine a diverse geometrie CONSISTENTI.Qual è quella giusta? Lo sono tutte! Quale descrive questo universo? Questa è FISICA!