このトピックに関するフィッシャー教授のノート（PDF）
このトピックに関するフィッシャー教授のスライド（PDF、パスワード必要）
セクラ教授の古いスライド（PDF）

Induction

注：（教授も含め）哲学者たちは、このようなトピックに関心を示しているのだ。 フィッシャー教授を含む哲学者は、帰納（あるサンプルの特徴を他のものに一般化すること）とアブダクション（最良の説明への推論）を区別していますが、以下の内容は、この両者を「帰納」という一つの見出しで曖昧にしています。 9017>

帰納法とは、ある現象のサンプルを研究することによって、その仕組みを解明しようとするプロセスである。 誘導は創造的なプロセスである。 科学者は、現象のサンプルを慎重に研究し、次にその現象を説明するための仮説を立てなければなりません。最も素晴らしい研究結果を得る科学者は、正しい研究課題を考えるのに十分創造的である人です。 具体的な結果（サンプル）から始めて、一般的な法則を推測する。 仮説は反証されるだけで、証明されることはない。 仮説が多くの独立した研究者によって繰り返し試されることに耐えるならば、その仮説に対する信頼は高まる。 すべての仮説は暫定的なものであり、明日にでも覆る可能性があるが、「法則」や「事実」を覆すには非常に強い証拠が必要である。 大きな袋に入ったビー玉の中からランダムに20個のビー玉を取り出したとします。 そのすべてが白であることがわかった。 これは私の観察で、取り出したビー玉はすべて白かったのです。 したがって、私は、袋の中のすべてのビー玉が白であれば、これは説明されるという仮説を立てることができました。

ちなみに、これは仮説が正しいことを証明できる場合の一つで、袋の中のビー玉を全部捨てて、一つ一つを調べればよい。 帰納法が使われるほとんどの場合、センサスは実行不可能です。

帰納法。 9267>

これは推論の方法で、演繹法のように厳密ではありません。 あなたは、何がその観測を説明するのか、すぐにはわからない。 これは、演繹法とは異なり、創造的なプロセスである。 これは推論とは異なり、創造的なプロセスです。これがうまく機能するためには、状況について可能な限り多くのaspossibleを知っている必要があります。 あなたが知っているすべてのことを考えると、あなたは最も合理的で可能性が高いと思われる仮説を選択します。 このような推論は、シャーロック・ホームズの得意とするところである。 コナン・ドイルの有名な超観察力のある探偵は、警視が通常見逃す非常に小さな手がかりにさえ気づきます。 ホームズはその手がかりと、これまで培ってきた事件に関する一般的な知識を組み合わせて、「誰が犯人なのか」という最良の説明を導き出す。 また、読者にとって嬉しいことに、ホームズはしばしば解決に至った理由を説明します。 ホームズが説明すると、簡単そうに見えますが…

Deduction

Mathematics is a deductive science.数学は演繹的科学である。 公理は提案される。 それらは検証されず、真であると仮定される。 定理は公理から演繹される。 公理と論理の規則があれば、機械は定理を作り出すことができる。

一般->特定

一般規則から始めて、特定の結果を導く。公理の集合が定理とその否定を作り出す場合、公理の集合は不一致と呼ばれる。

以下の既知の条件を持っていると仮定する。

• 大きなビー玉の袋がある。
• 袋の中のビー玉はすべて白いことが分かっている。
• 袋からランダムに20個のビー玉を採取した。

これらから、見ずともサンプル中のビー玉はすべて白いと推論することが可能である。 このような推論をmodus ponensといいます（詳しくは後述、フィッシャー先生のノートにあります）。

これはどうでしょう。

• 私たちは大きな袋の中にビー玉が入っています。
• 袋の中のビー玉はすべて白です。
• 私は色の混ざったビー玉20個のサンプルを持っています。

このことから、サンプルは白いビー玉の袋から取ったのではないことがすぐに推測されます。 このような推論をmodus tollensといいます（詳細は後述、フィッシャー先生のノート）。

演繹的議論

ここで、演繹的推論の考え方を見てみましょう（フィッシャー先生のノートから派生）。フィッシャー教授は、哲学者は通常、これを

1. Premise number 12. Premise number 2...------------------------C. Conclusion to be reached

この構造が議論を構成すると述べている。
P =>C (Premises imply Conclusion, just like above)
これは、前提が真ならば、結論も真であることを意味する。
「良い議論であるためには、真の前提があって、前提が結論を支持しなければならない」。 最も強力な支持は、結論が真であることを絶対的に保証するものである（もちろん、前提が真であることを前提とする）。”まずその種の支持を検討するが、その後、いくつかの弱い種類の支持も検討する。 (フィッシャー教授より)
特に有用な種類の論証に、演繹的に妥当な論証があります。 (これはしばしば「有効な議論」と略されたり、「演繹的議論」と呼ばれたりする。）演繹的に有効な議論とは、前提がもし本当なら、結論が本当であるという最も強い可能な証拠となるような議論のことである。 実際、これらの論証は次のような保証を提供している：前提が真であれば、結論も真でなければならない。
演繹的に見えるが、結論を支持しない（保証しない）前提を持つ論証は無効論証である。
P => C（前提が結論を導く）の三段論法を繰り返そう。これについては、4つの主張が考えられる。

1. すべての前提が真である（Pは真）（モーダスポーンズ推論）
2. 1つ以上の前提が偽である（Pは偽-、Cは偽-）

。 Pではない）

3. 結論は真（Cは真）
4. 結論は偽（Cは偽-Cではない）（modus tollens reasoning）

このうち演繹的に妥当な推論は二つ（＃1、＃4）だけである。その理由を1つずつ見ていきましょう。

1. P is true (P) – 先行詞を肯定する。 すべての前提が真であれば、結論も真でなければならない。 これは非常に強い主張である。 (modus ponens)
2. P is false (not P) – 先行詞を否定する。 Pが偽であることは、Cが真か偽かを保証するものではありません。
3. C is true (C) – 帰結を肯定する。
4. C is false (not C) – 帰結を否定している。 ここで、もしCが偽であればPも偽でなければならない。 もしPが真であればCも真であろう。 (modus tollens)

要するに、#1と#4（modus ponensとmodus tollens）は演繹的に有効で、#2と#3は無効である。 3350>

さて、ここでベン図を話題にします。

Venn Diagrams

Venn Diagram は論理を表現するグラフィック手法です。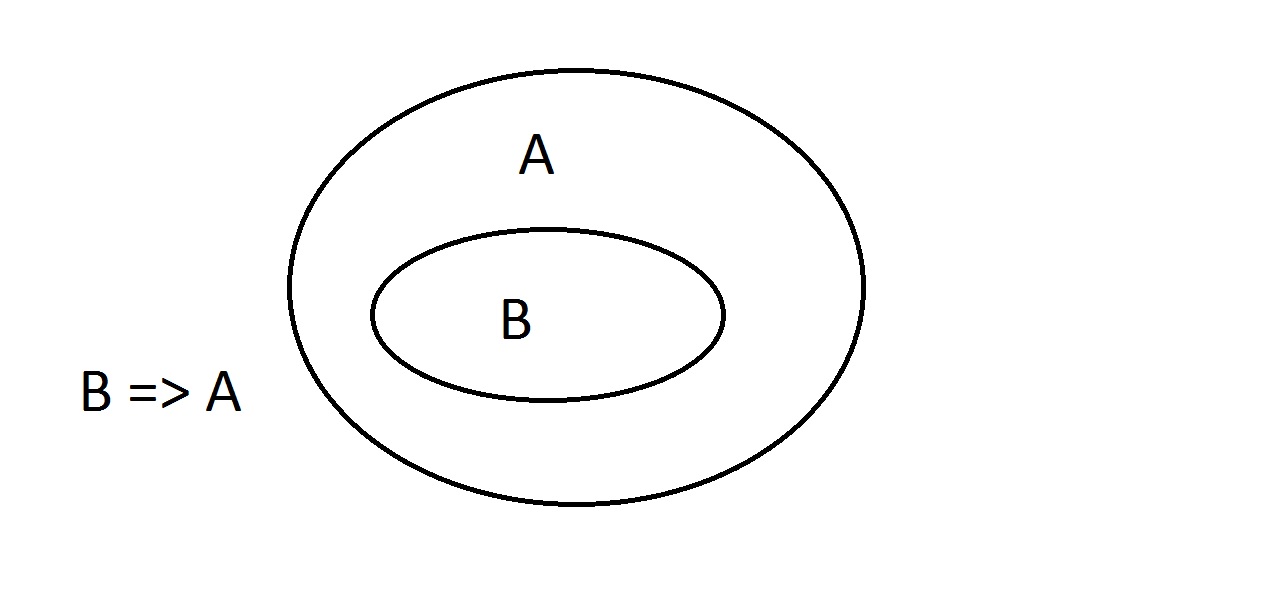
これは最もシンプルな図です。 外側の楕円には性質Aを持つものがすべて入っており、内側の楕円には性質Bと性質Aを持つものがすべて入っています。これはB=>Aとして示されており、性質Bを持つものはすべて性質Aも持つことを意味します。 これは前述した保証である。
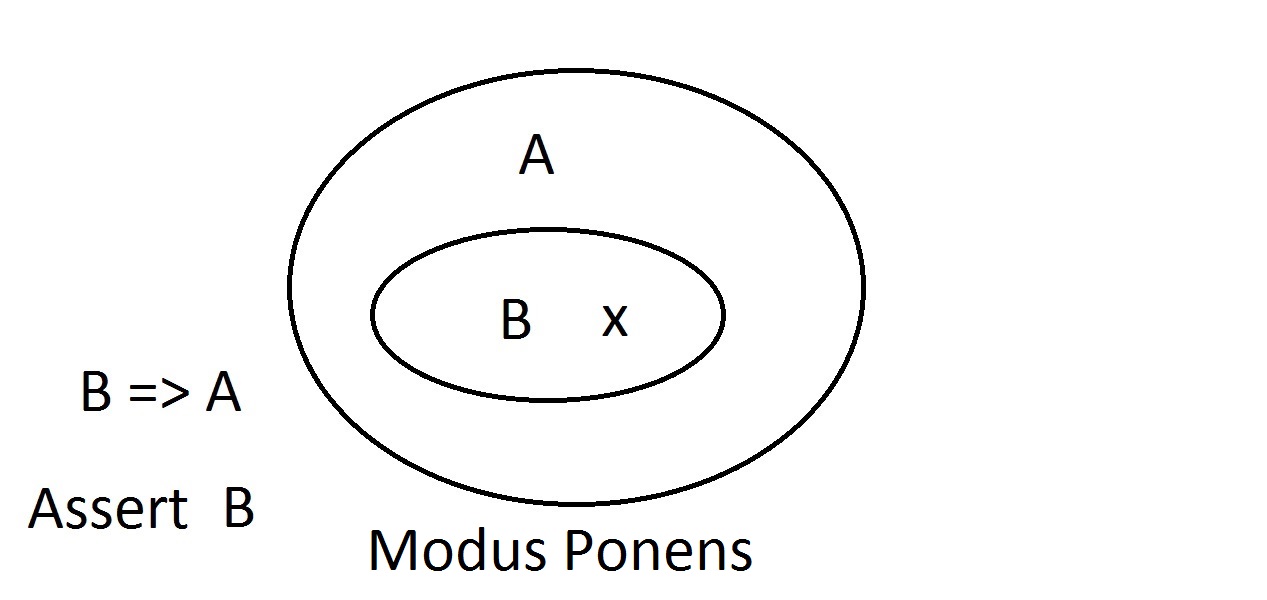ここで、性質Bを持つものがあると主張する。 このとき、私たちは自信をもって「Aという性質も持っている」と主張することができます。 これはModus Ponens（先行詞を肯定する）推論である。
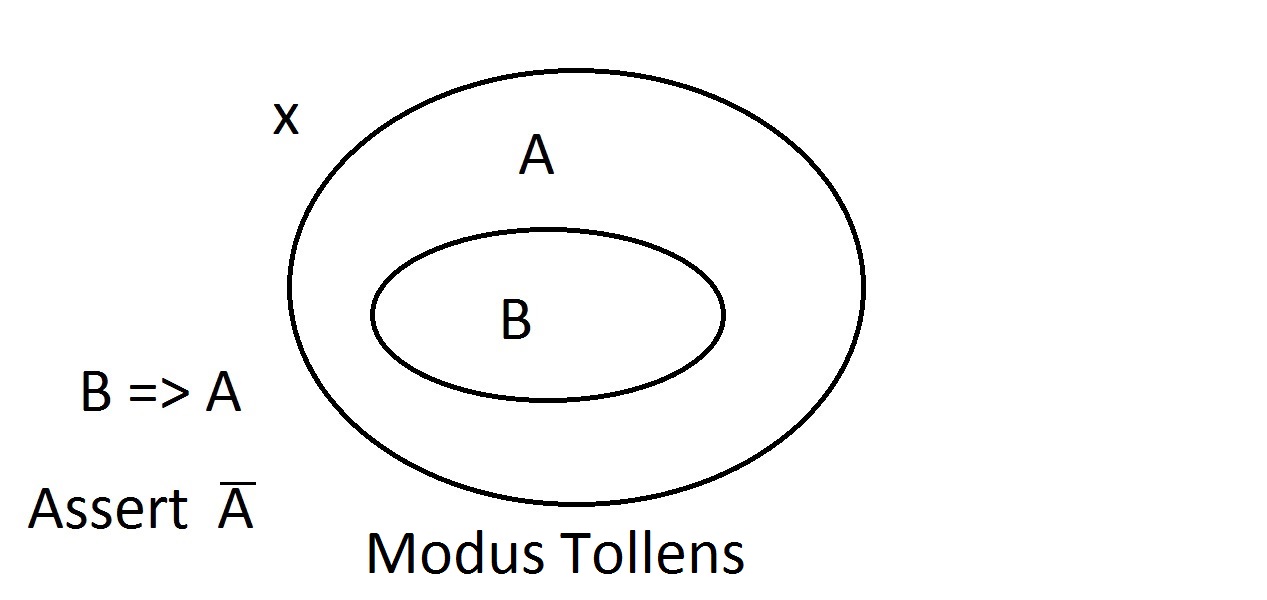今、ある実体が特性Aを持たないと主張したとする。ベン図は、それが特性Bも持つことができないことを示している。 特性A空間の外側にあるものは、特性B空間の外側にもあるはずです。 これはModus Tollens（帰結を否定する）推論であり、有効で強い。
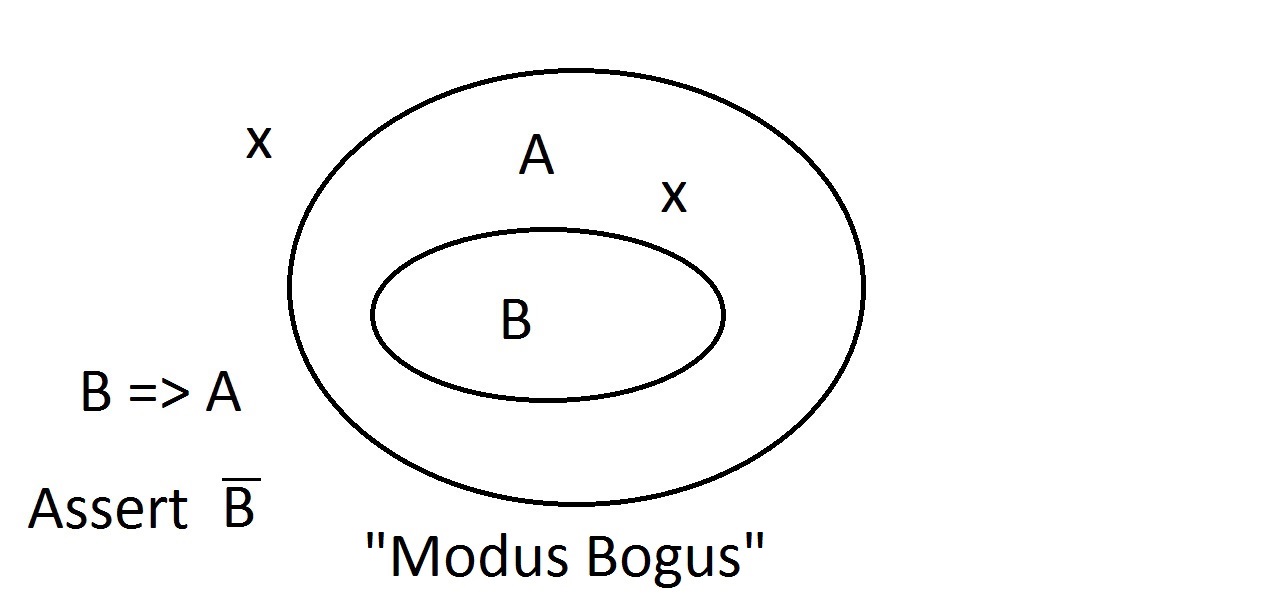ここで、我々のものが性質Bを持たないことを主張してみる。 ベン図を見ると、ここが問題であることがわかる。 特性Bを持たない実体は、A空間の内側にあることもあれば、外側にあることもある。 Bでない」という主張はAについて何も語っていない。これは有効な推論ではないので、我々はこれをModus Bogusと呼んだ。 これは先行詞の否定であり、妥当ではない。
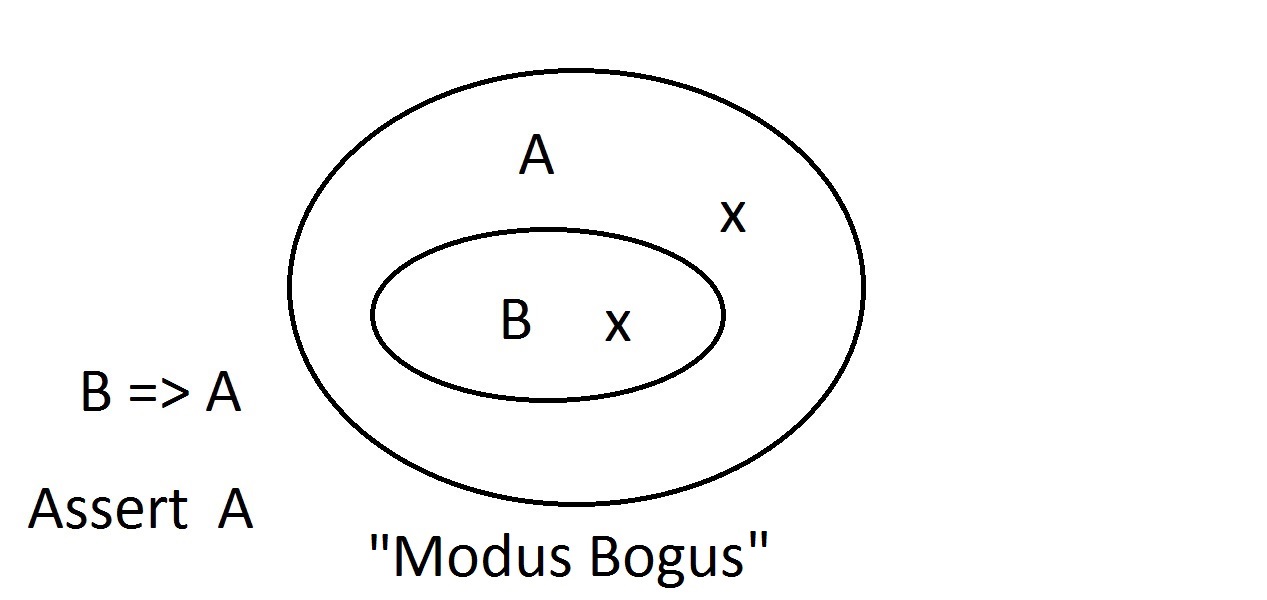最後の可能性は、我々のものが特性Aを持っていると主張することである。 実体はA空間のどこにでもあり得るし、B空間の内側にも外側にもあり得る。 これはModus Bogus、つまり無効な推論であり、Affirming the Consequentと呼ばれています。
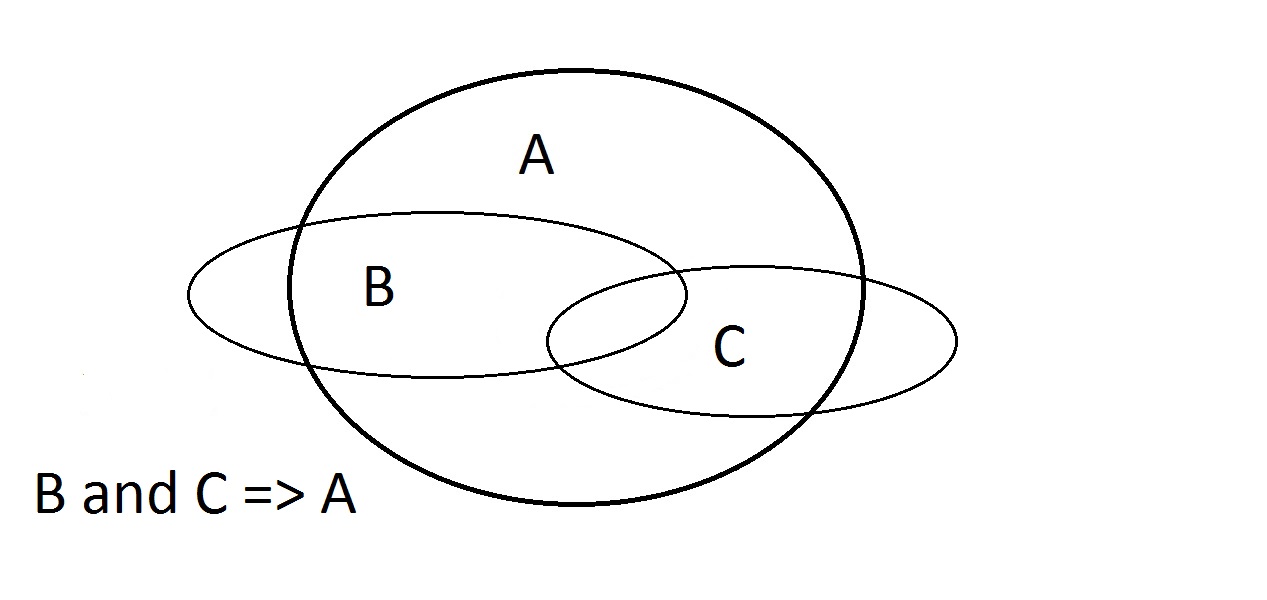ここでは特性A、B、Cを扱っていますが、BとCを持つ実体はAも持つことだけが保証されます。

• Assert A: Aのどこでもよい
• Assert B: BのいくつかはAの外にある
• Assert C: CのいくつかはAの外にある
• A and B: あるCを含むかもしれないし含まないかもしれないと仮定する。
• Assert B and C: 交点BCは完全にAの中にある。B and C => Aという論証は有効。
• Assert C: Bを含むかもしれない、含まないかもしれない

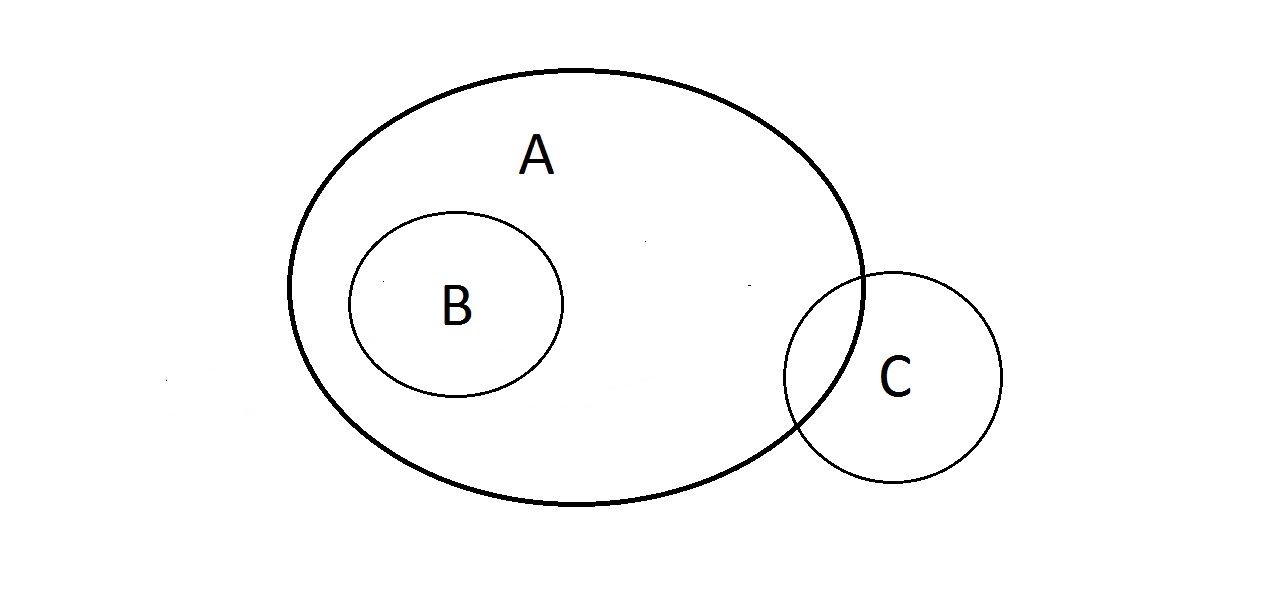
これをどうすればいいのでしょうか。 性質A、Bは上記の通りですが、Cはどうでしょうか。 性質Cを持つものは、Aの中にあるかもしれないし、ないかもしれない。 Aの中にあるものはCの中にもあるかもしれないし、ないかもしれない。 ここでCをどうこうすることはできません。 Bを持つものはAも持っているという保証はあります。

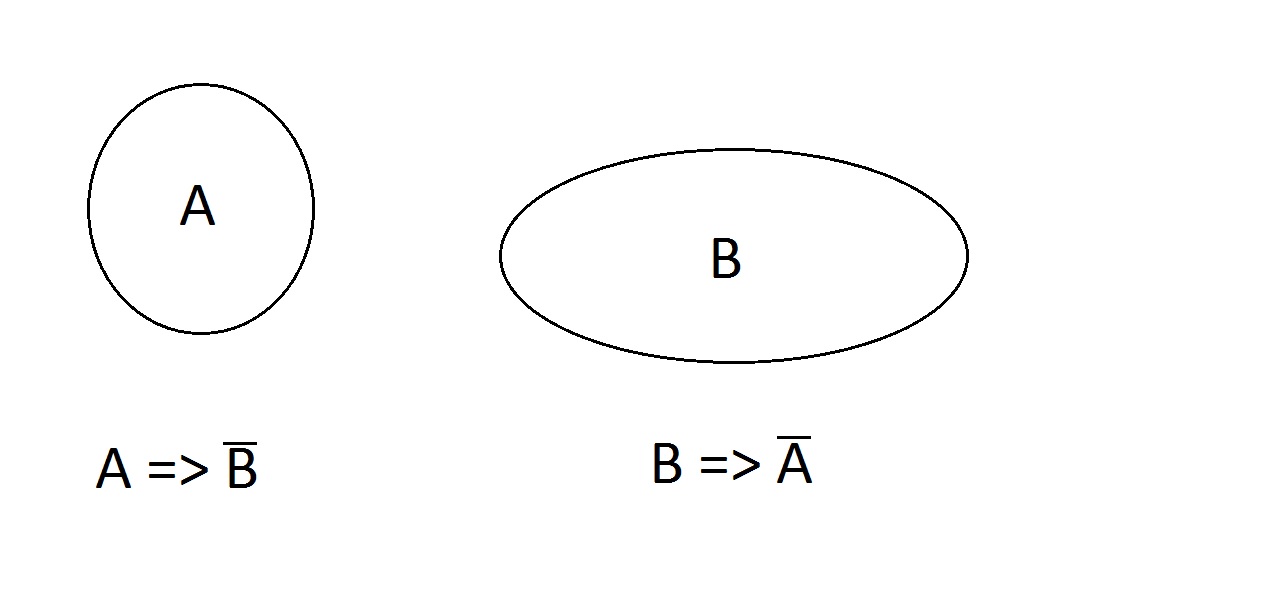
こんなのはどうでしょう。 この性質は排他的であり、ある実体が同時に両方を持つことはできません。それは、何も持たず、AもBも持つことができますが、ABは持つことができません。 A=>ではなくB、B=>ではなくAという記述は有効です。
最後に、我々は我々の議論が健全であることを望んでいます。 このためには、論証は上記のように演繹的に妥当でなければならず、前提は現実の世界において真でなければならない。

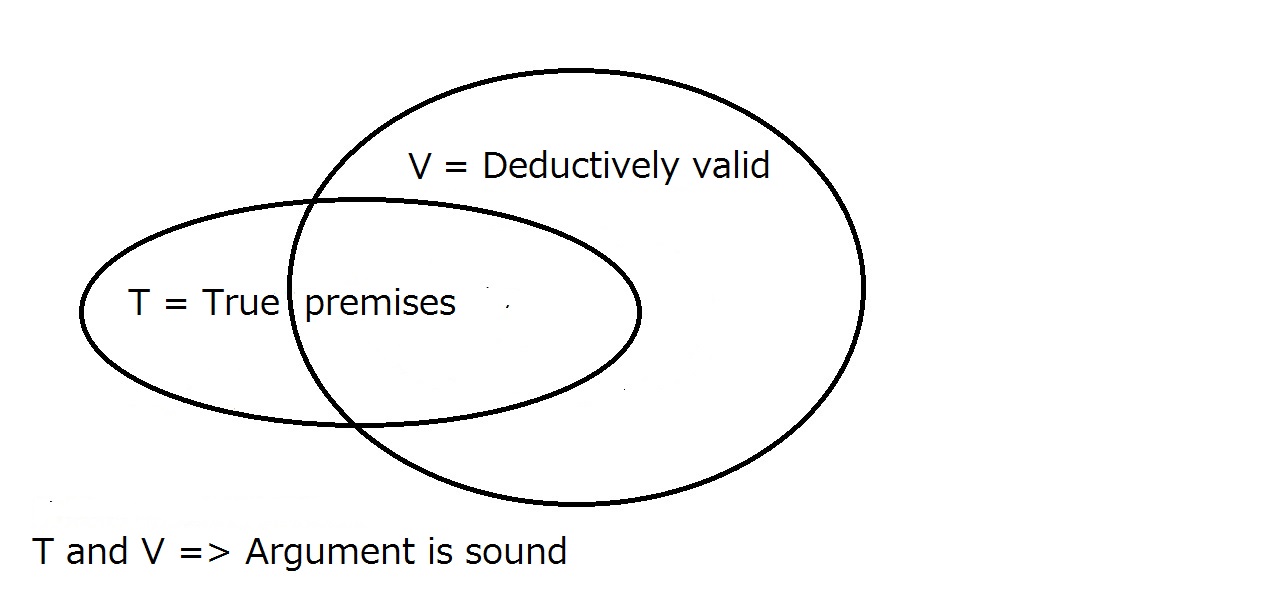
健全な議論は、それが演繹的に有効であることと、真の前提を持っていることを必要とすることを意味します。 TとVの両方の内側にある領域が、健全な議論の領域である。

私が考える方法はこうだ。 9267>

Aristotle (BCE 384-322)

http://www.rwe.org/images/aristotle.jpgExperimentより?
Self-consistent?
あなたの理論が自己一致しない場合、またはあなたの理論が慎重な実験に不一致の場合はあなたの理論は間違っています。

Galileo Galilei (1564-1642)

http://helios.gsfc.nasa.gov/galileo.jpgより

例えばユークリッドの第5仮定

(1) 異なる2点を通して、1本の線を引くことが可能である。
(2) 有限な直線は連続して直線状に伸ばすことができる
(3) 円は任意の点を中心とし、任意の距離を半径として記述できる
(4) すべての直角は等しい
(5) 任意の点を通って、任意の直線に平行な直線は1本だけ引くことができる
。
「点」と「線」は本質的な意味を持たない。
「点」と「線」を入れ替えても、真の定理が成り立つ。
以下のように言える。(1) 任意の2つの異なるブラッグを通して、1つのフレームを描くことが可能。
第5仮定は2つの方法で変更できます：
(5) 与えられた点を通って、与えられた線に平行な線は引けない。
(5) 与えられた点を通って、与えられた線に平行な多くの線を引ける。
これらの新しい仮定は両方とも異なる一貫した幾何学を生じさせる。 すべてそうです。 どれがこの宇宙を記述しているのか、それが物理学です！