Nota do Professor Fisher sobre este tópico em PDF
Diapositivos do Professor Fisher sobre este tópico em PDF (senha requerida)
Diapositivos antigos do Professor Sekula em PDF.

Indução

Nota: Filósofos (incluindo Prof. Fisher) distinguem a indução (generalizando os traços de algumas amostras para outras coisas) da abdução (inferência para a melhor explicação), enquanto que o conteúdo abaixo embaça ambos juntos sob o título único de “indução”. Ao fazer esta aula com o Professor Fisher, é melhor confiar nas suas notas ou slides sobre este tópico, do que no conteúdo abaixo.

Indução é um processo de tentar perceber o funcionamento de algum fenómeno através do estudo de uma amostra do mesmo. Você trabalha com uma amostra porque olhar para cada componente do fenômeno não é viável. A indução é um processo criativo. O cientista deve estudar cuidadosamente uma amostra de um fenômeno, depois formular uma hipótese para explicar o fenômeno. O processo científico de testar a hipótese segue.Os cientistas que obtêm os resultados mais espetaculares da pesquisa são aqueles que são criativos o suficiente para pensar nas questões certas da pesquisa.

As ciências naturais (física, química, biologia, etc.) são indutivas.As evidências são coletadas. O Método Científico é aplicado. Comece com resultados específicos (uma amostra) e tente adivinhar as regras gerais. Hipóteses só podem ser refutadas, nunca provadas. Se uma hipótese resiste a ensaios repetidos por muitos investigadores independentes, então a confiança cresce na hipótese. Todas as hipóteses são tentativas; qualquer uma poderia ser revertida amanhã, mas são necessárias provas muito fortes para derrubar “Lei” ou “Fato”.

Específico -> Geral

Aqui está um exemplo de indução: Suponha que tirei 20 berlindes ao acaso de um grande saco de berlindes. Cada um deles acabou sendo branco. Essa é a minha observação – todos os mármores que tirei eram brancos. Eu poderia então formar a hipótese de que isso seria explicado se todos os mármores no saco fossem brancos. Poderia ser que houvesse alguns mármores varicolores no saco e minha primeira amostra simplesmente não atingiu nenhum.

Inicialmente, este é um caso em que poderíamos provar que a hipótese é verdadeira. Na maioria dos casos em que a indução é usada, um censo não é viável.

Abdução: Inferência à Melhor Explicação

Este é um método de raciocínio que não é rigoroso como a Dedução.Suponha que você tenha observações de uma ocorrência interessante. Você tem a certeza imediata do que explica as observações. Você pensa em todas as hipoteses que você pode que poderiam explicar plausivelmente as observações. Este é um processo criativo, ao contrário da dedução. Você precisa saber o máximo possível sobre a situação para que isto funcione bem. Dado tudo o que você sabe, você seleciona a hipótese que parece mais razoável e provável. Você escolheu a aparente melhor explicação, embora possa estar errada. Não há nenhuma garantia. A verificação da sua explicação é normalmente uma boa ideia se for possível; poderá encontrar mais informações que o levem a reconsiderar a sua conclusão.

Este tipo de raciocínio é o forte de Sherlock Holmes. Conan Doyle é um detetive hiper-observantemente hiper-observante que percebe até mesmo pequenas pistas que o inspetor da polícia geralmente não percebe. Holmes combina estas pistas com o conhecimento geral que construiu sobre o caso para chegar à bestexplanação – o que é mais importante! Ele também explica como o crime foi feito. Num toque agradável para o leitor, Holmes explica muitas vezes o raciocínio que o levou à solução. Parece simples quando Holmes o explica…

Dedução

Matemática é uma ciência dedutiva. Os axiomas são propostos. Eles não são testados; eles são assumidos como verdadeiros. Os teoremas são deduzidos a partir dos axiomas. Dados os axiomas e as regras de lógica, uma máquina poderia produzir teoremas.

Geral ->Específico

Comece com a regra geral e deduza resultados específicos.Se o conjunto de axiomas produz um teorema e uma itsnegação, o conjunto de axiomas chama-se INCONSISTENTE.

Suponha que temos as seguintes condições conhecidas.

• Temos um grande saco de mármores.
• Todos os mármores do saco são conhecidos por serem brancos.
• Tenho uma amostra aleatória de 20 mármores retirados do saco.

Destes, posso deduzir que todos os mármores da amostra são brancos, mesmo sem olhar para eles. Este tipo de raciocínio é chamado modus ponens (mais sobre isto abaixo e nas notas do Prof. Fisher).

Como sobre isto?

• Temos um grande saco de berlindes.
• Todos os mármores do saco são brancos.
• Eu tenho uma amostra de 20 mármores de cores mistas.

Disso deduzo rapidamente que a amostra não foi retirada do saco de mármores brancos. Este tipo de raciocínio chama-se modus tollens (mais sobre isto abaixo e nas notas do Prof. Fisher).

Argumentos dedutivos

Vejamos a ideia do raciocínio dedutivo (derivado das notas do Prof. Fisher).Aqui estamos falando de fazer um argumento para alguma idéia ou conclusão baseada em um conjunto de premissas (fatos, idéias, etc.).Prof. Fisher observa que os filósofos geralmente mostram isso como

1. Premise number 12. Premise number 2...------------------------C. Conclusion to be reached

Esta estrutura constitui um argumento.Às vezes é escrito como
Premissas 1, Premissa 2, Premissa… =>Conclusão.
Vamos abreviar isto no silogismo assim:
P =>C (Premissa implica Conclusão, tal como acima)
Isto significa simplesmente que se as premissas são verdadeiras, então a conclusão também é verdadeira.
“Para ser bom, um argumento deve ter premissas verdadeiras e as premissas devem oferecer suporte para a conclusão. O apoio mais forte possível daria uma garantia absoluta de que a conclusão será verdadeira (presumindo, é claro, que as premissas são verdadeiras). (do Prof. Fisher)
Um tipo de argumento especialmente útil é um argumento válido do ponto de vista dedutivo. (Isto é muitas vezes abreviado como “argumento válido” ou às vezes como “argumento dedutivo”.) Argumentos dedutivamente válidos são argumentos em que as premissas, se verdadeiras, seriam a evidência mais forte possível de que a conclusão é verdadeira. De facto, estes argumentos fornecem a seguinte garantia: se as premissas são verdadeiras, então a conclusão também deve ser verdadeira.

Um argumento que parece ser dedutivo mas tem premissas que não apoiam a conclusão (sem garantia) é um argumento inválido.
Vamos repetir o silogismo P => C (As premissas levam à conclusão).Há quatro afirmações possíveis que você poderia fazer sobre isso:

1. Todas as premissas são verdadeiras (P é verdadeiro) (modus ponens reasoning)
2. Uma ou mais premissas é falsa (P é falso – não P)
3. A conclusão é verdadeira (C é verdadeiro)
4. A conclusão é falsa (C é falso – não C) (modus tollens raciocínio)

Só dois destes (#1 e #4) constituem um raciocínio dedutivamente válido.Vejamos a razão disto, uma escolha de cada vez.

1. P é verdadeiro (P) – Afirmando o antecedente. Se todas as premissas são verdadeiras, a conclusão deve ser verdadeira. Este é um argumento muito forte. (modus ponens)
2. P é falso (não P) – Negar o antecedente. P sendo falso não garante que C seja verdadeiro ou falso. Pode haver outras causas.
3. C é verdadeiro (C) – Afirmando o conseqüente. Se C é verdadeiro pode ser antes de uma das várias razões, não este P.
4. C é falso (não C) – Negando o conseqüente. Aqui, se C é falso entãoP também deve ser falso. Se P fosse verdadeiro C também seria. (modus tollens)

Em resumo, #1 e #4 (modus ponens e modus tollens) são dedutivamente válidos enquanto #2 e #3 não são.
Se as premissas se aplicam a coisas no mundo real, você ainda precisa testar a invalidez. Há pelo menos três abordagens.

1. Veja se você pode encontrar um cenário em que as premissas são verdadeiras, mas a conclusão em falso.
2. Try substituindo um substantivo ou adjetivo no argumento por outro.Substitua todas as instâncias. Se isto não for obviamente válido, então o original não era válido.
3. Representar P e C em um diagrama Venn.Se você puder fazer isto para que P seja verdadeiro mas C seja falso, o argumento é inválido. Nós fizemos estes diagramas para você abaixo.

Agora trazemos à tona o assunto dos diagramas Venn. Estes podem ser de grande valor na verificação das premissas de um argumento.

Diagramas Venn

Diagramas Venn são um método gráfico de representação da lógica.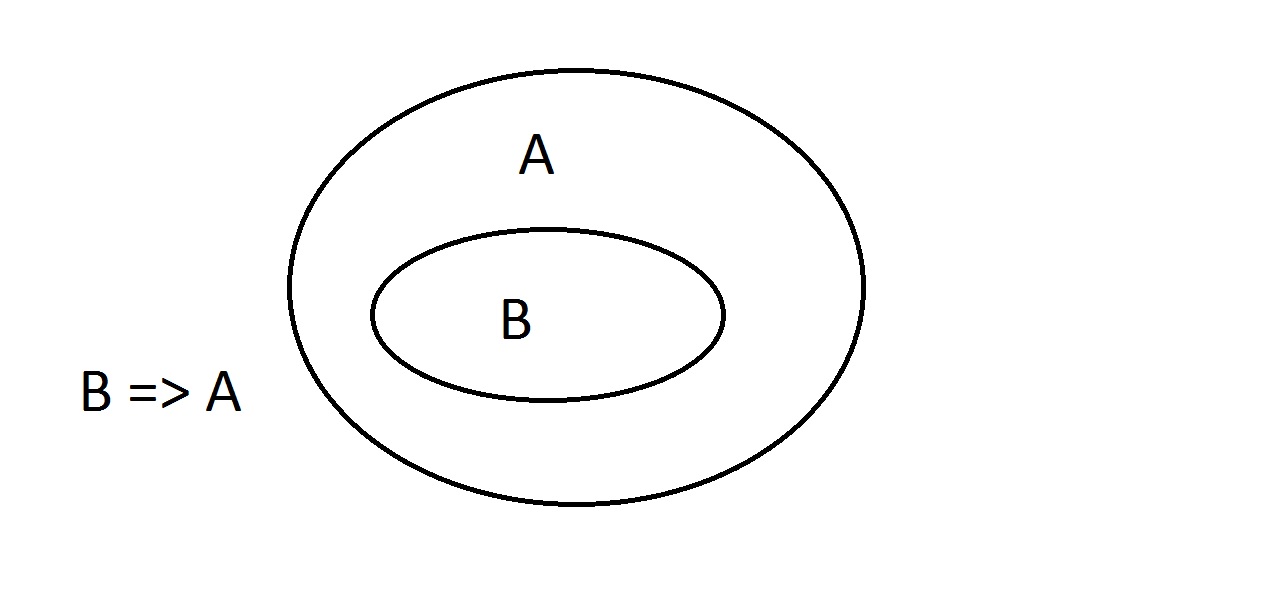
Este é o diagrama mais simples que você vai obter. A oval externa contém todas as coisas com propriedade A, enquanto a oval interna contém todas as coisas com propriedade B bem como a propriedade A. Isto é mostrado como B=>A, o que significa que todas as coisas com propriedade B também têm propriedade A. Você também poderia dizer “B implica A.” Se B é verdade, então A deve ser também. Esta é a garantia mencionada acima.
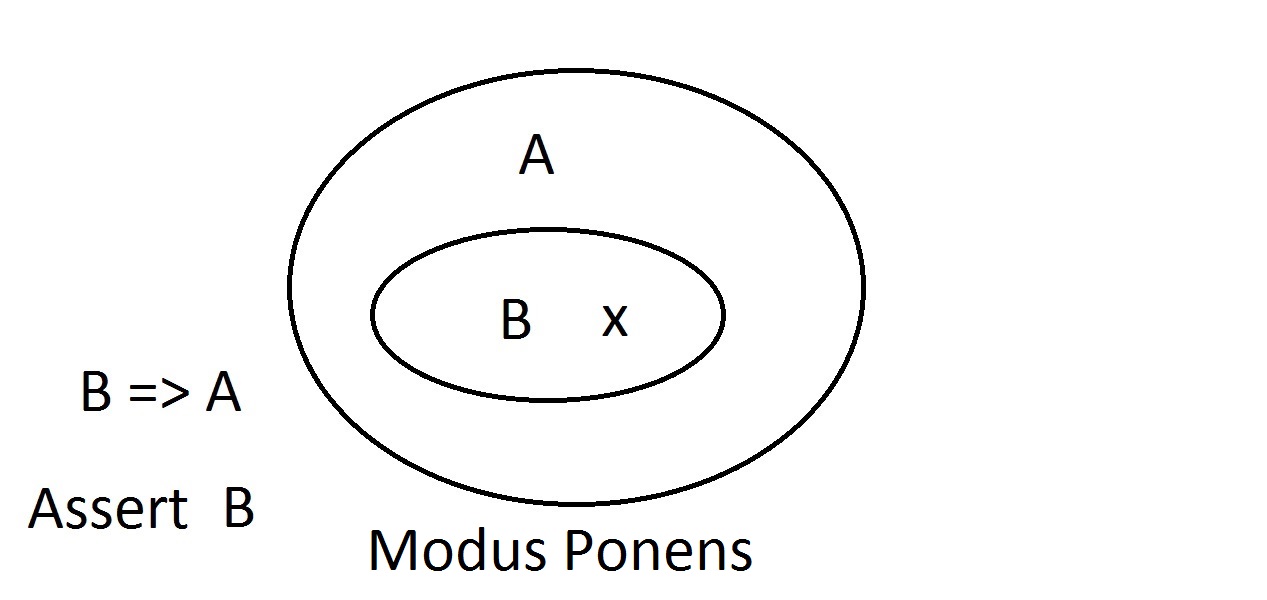A. Agora vamos afirmar que temos algo com a propriedade B. Podemos argumentar com confiança que ithas propriedade A também. Este é o raciocínio do Modus Ponens (afirmando o anterior). Qualquer entidade com propriedade B obviamente também deve estar no espaço da propriedade A.
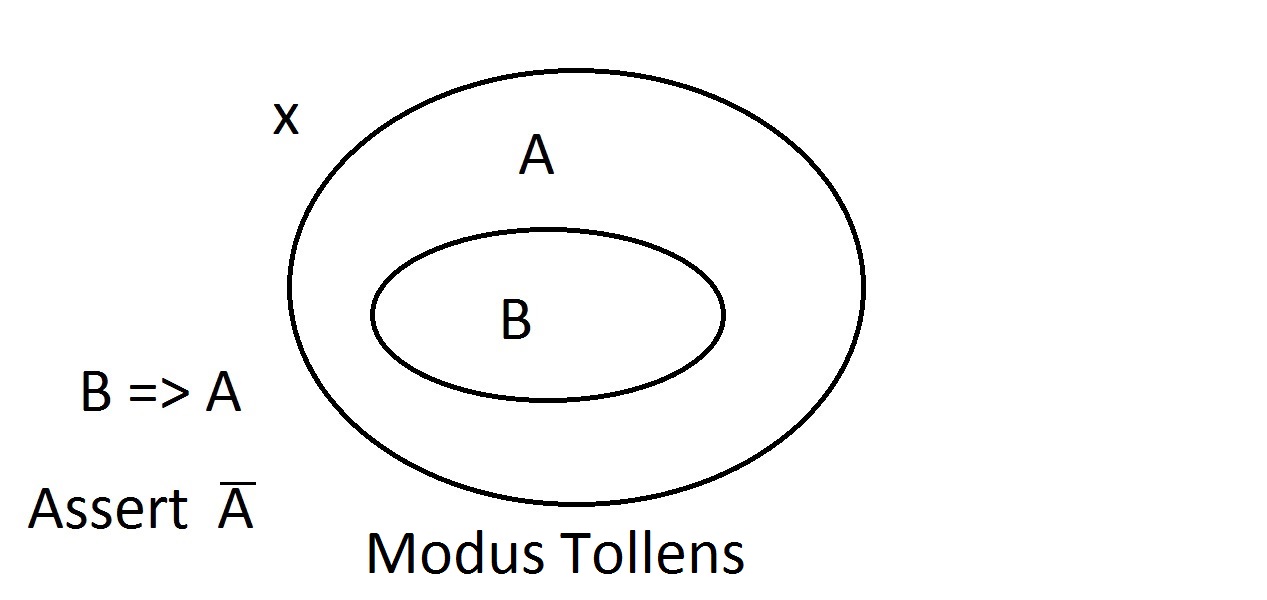Agora afirmamos que uma entidade não tem propriedade A. O diagrama Venn mostra que ela também não pode ter propriedade B. Qualquer coisa fora da propriedade A deve também estar fora do espaço da propriedade B. Isto é Modus Tollens (negando o conseqüente) raciocínio e é válido e forte.
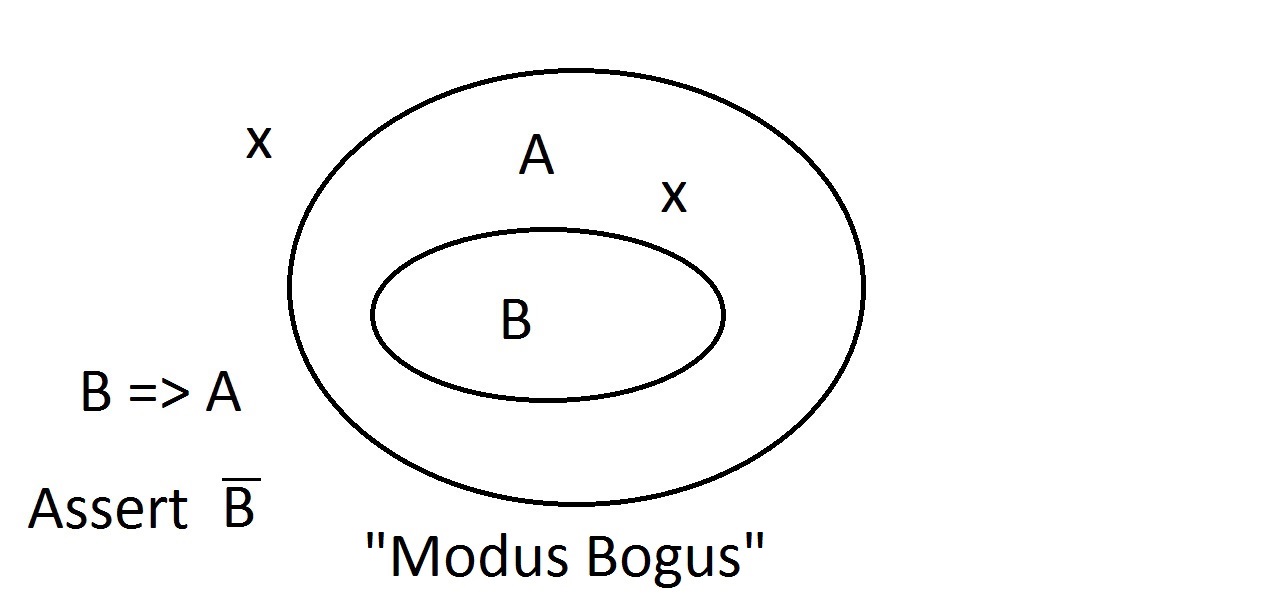Agora vamos tentar afirmar que nossa coisa não possui a propriedade B. Um olhar para o diagramaVenn mostra o problema aqui. Uma entidade que não possui a propriedade B pode estar dentro do espaço A ou fora dele. A afirmação de “não B” não nos diz nada sobre A. Isto não é um raciocínio válido, por isso chamamos-lhe Modus Bogus. É Negar o Antecedente e não é válido.
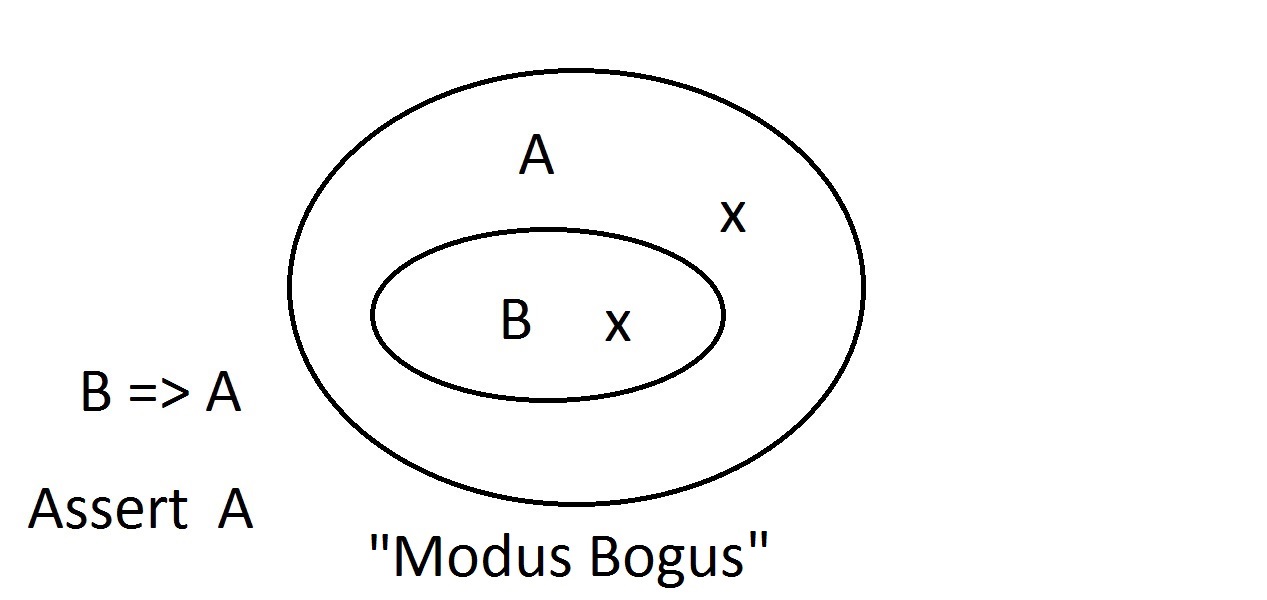A possibilidade final é afirmar que a nossa coisa tem propriedade A. O diagrama Venn mostra o problema. A entidade pode estar em qualquer lugar do espaço A, seja dentro ou fora do espaço B. Asserting that the thing has Atells you nothing about whether it has also B. This is also Modus Bogus, or invalid ragement.It is called Affirming the Consequent.
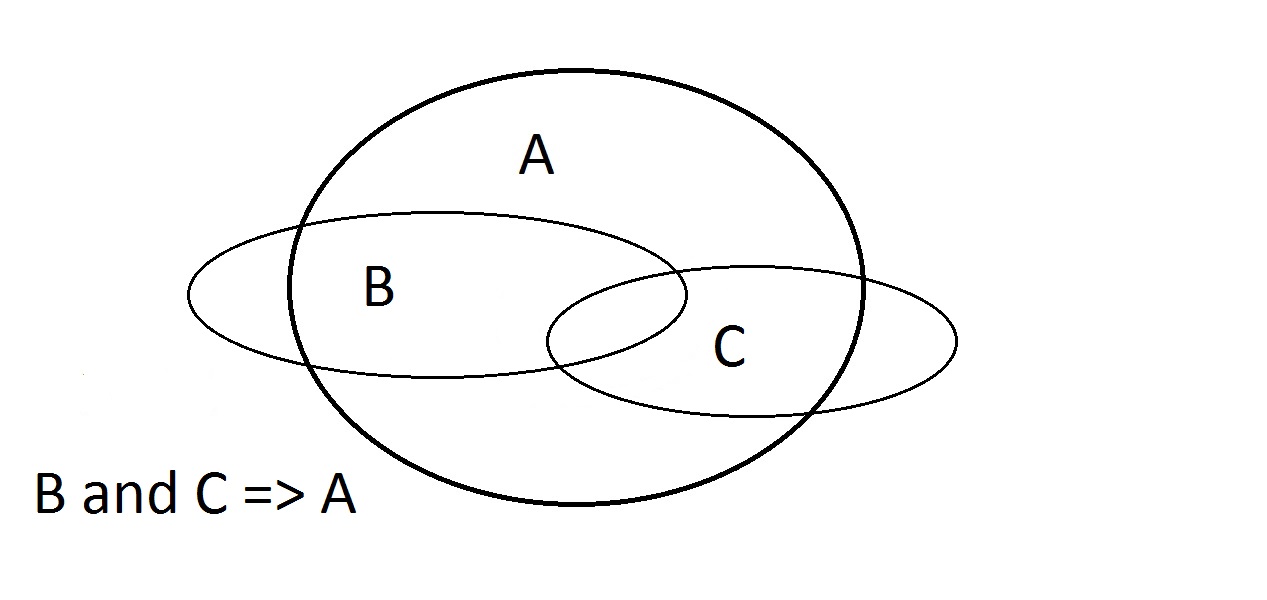Here estamos lidando com as propriedades A, B, e C. Aqui podemos garantir apenas que uma entidade tendo B e C também tem A.Note que alguns dos espaços B e C estão fora do espaço A.

• Inserção A: Pode estar em qualquer lugar em A
• Inserção B: Alguns de B estão fora de A
• Inserção C: Alguns de C estão fora de A
• Inserção A e B: Pode incluir algum de C; pode não incluir.
• Inserção B e C: A intersecção BC encontra-se inteiramente em A. Argumentando que B e C =>A funciona.
• Inserção A e C: Pode incluir algum B; não pode

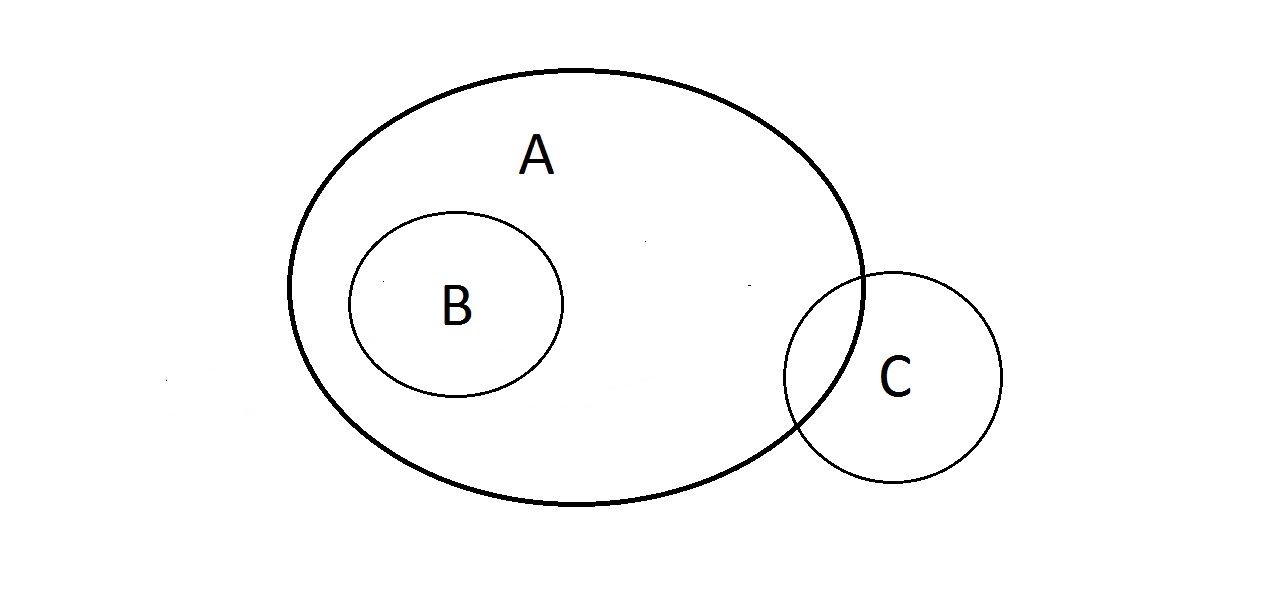
O que se pode fazer com isto? As propriedades A e B são como acima, mas e quanto a C? Algo que tenha a propriedade C pode estar dentro da propriedade A ou não. Alguma coisa em A também pode estar em C ou não. Você não pode fazer nada com C aqui. Nós temos a garantia que algo tendo B também tem A.

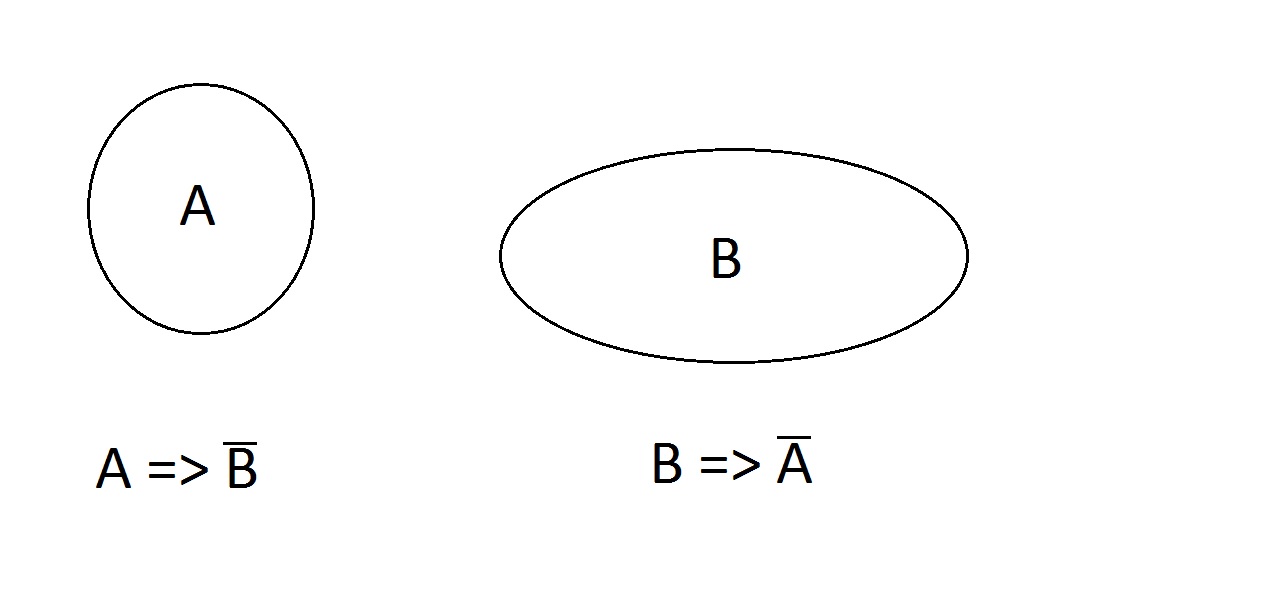
Como sobre isto. As propriedades são exclusivas; uma entidade não pode ter ambas ao mesmo tempo. Ela não pode ter nenhuma, A, ou B, mas não AB. As afirmações A=> não B e B => não A são válidas.
Finalmente, queremos que o nosso argumento seja sólido. Para que isso aconteça, o argumento deve ser válido como acima e as premissas devem ser verdadeiras no mundo real. Isto significa que todos os argumentos sólidos são válidos mas todos os argumentos válidos não são necessariamente sólidos.

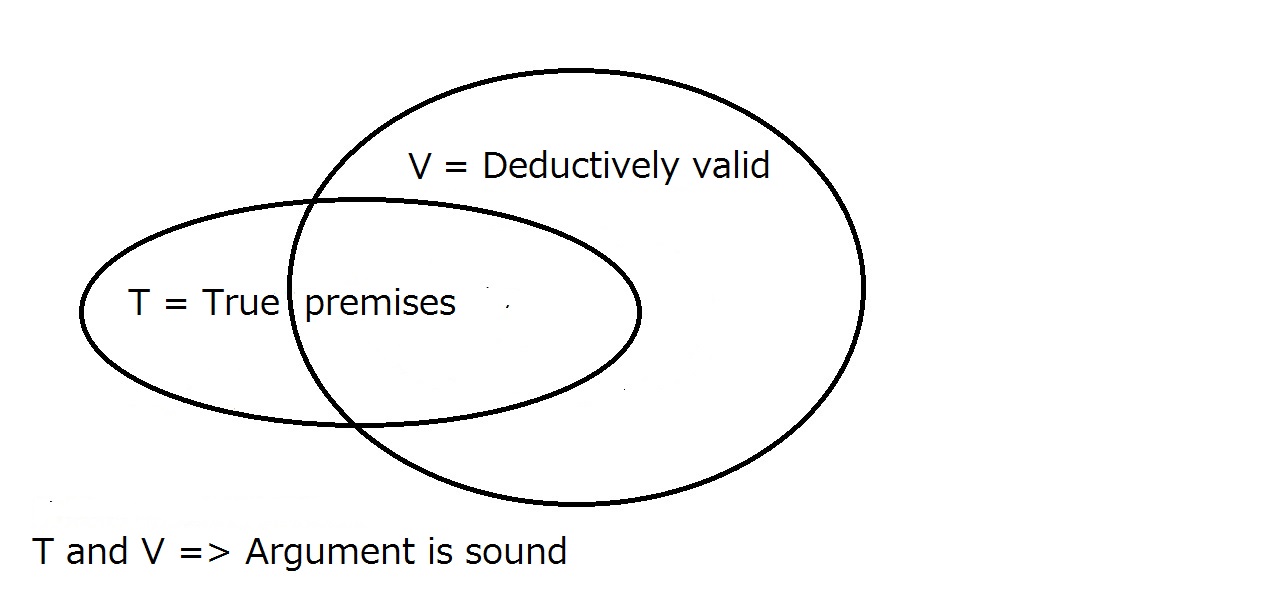
Um argumento sólido requer que ele seja dedutivamente válido e tenha premissas verdadeiras.Ter um não garante automaticamente o outro. A região que está dentro de T e V é a região dos argumentos sonoros.

Aqui está a minha maneira de ver. Todo mundo me escute.

Aristóteles (384-322 a.C.)

De http://www.rwe.org/images/aristotle.jpgExperiment?
Self-consistente?
Se sua teoria não é autoconsistente, ou se sua teoria discorda de experimentos cuidadosos, então sua teoria está errada. Não importa quão bonita a teoria seja; está errada.

Galileo Galilei (1564-1642)

De http://helios.gsfc.nasa.gov/galileo.jpg

e.g. o quinto postulado de Euclides.

(1) Através de quaisquer dois pontos diferentes, é possível traçar uma linha.
(2) Uma reta finita pode ser estendida continuamente em uma reta.
(3) Um círculo pode ser descrito com qualquer ponto como centro e qualquer distância como raio.
(4) Todos os ângulos rectos são iguais.
(5) Através de um dado ponto, apenas uma reta pode ser desenhada paralelamente a uma dada reta.
As palavras “ponto” e “linha” não têm significado intrínseco.
Uma poderia trocar “ponto” e “linha” e ainda ter teoremas verdadeiros.
Uma poderia dizer
(1) Através de quaisquer dois blargs diferentes, é possível desenhar uma fleem…
O quinto postulado pode ser alterado de duas maneiras:
(5) Através de um dado ponto, nenhuma linha pode ser desenhada paralelamente a uma dada linha.
(5) Através de um dado ponto, muitas linhas podem ser desenhadas paralelamente a uma dada linha.
Bambos estes novos postulados dão origem a diferentes geometrias CONSISTENTES. Qual delas está certa? Todas elas estão certas! Qual deles descreve este Universo? Isso é FÍSICA!