Poznámky profesora Fishera k tomuto tématu v PDF
Slidy profesora Fishera k tomuto tématu v PDF (vyžadováno heslo)
Starší slidy profesora Sekuly v PDF.

Indukce

Poznámka: Filozofové (včetně prof. Fisher) rozlišují indukci (zobecnění znaků nějakého vzorku na jiné věci) a abdukci (odvození nejlepšího vysvětlení), zatímco níže uvedený obsah směšuje obojí dohromady pod jediným názvem „indukce“. Při absolvování této hodiny s profesorem Fisherem je lepší spoléhat se na jeho poznámky nebo slajdy k tomuto tématu než na níže uvedený obsah.

Indukce je proces, při kterém se snažíme zjistit fungování nějakého jevu studiem jeho vzorku. Pracujete se vzorkem, protože zkoumání všechsložek jevu není proveditelné. indukce je tvůrčí proces. Vědec musí pečlivě prostudovat vzorek jevu a poté formulovat hypotézu, která tento jev vysvětluje. následuje vědecký proces testování hypotézy. nejpozoruhodnějších výsledků výzkumu dosahují vědci, kteří jsou dostatečně kreativní, aby vymysleli správné výzkumné otázky.

Přírodní vědy (fyzika, chemie, biologie atd.) jsou induktivní. shromažďují se důkazy. Uplatňuje se vědecká metoda. začněte s konkrétními výsledky (vzorkem) a pokuste se odhadnout obecná pravidla. Hypotézy lze pouze vyvracet, nikdy ne dokazovat. Pokud hypotéza vydrží opakované pokusy mnoha nezávislých výzkumníků, roste důvěra v hypotézu. Všechny hypotézy jsou předběžné; každá z nich může být zítra vyvrácena, ale k vyvrácení „zákona“ nebo „faktu“ je zapotřebí velmi silných důkazů.

Konkrétní -> Obecná

Tady je příklad indukce: Předpokládejme, že jsem náhodně vybral 20 kuliček z velkého pytle kuliček. Ukázalo se, že každá z nich je bílá. To je mojepozorování – každá kulička, kterou jsem vytáhl, byla bílá. Mohl bych si tedy vytvořithypotézu, že by se to vysvětlilo, kdyby všechny kuličky v pytli byly bílé. K ověření hypotézy by byl nutný další odběr vzorků. mohlo by se stát, že v sáčku jsou různobarevné kuličky a můj prvnívzorek prostě žádnou nezasáhl.

Náhodou je to jeden z případů, kdy bychom mohli prokázat pravdivost hypotézy. mohli bychom jednoduše vysypat všechny kuličky v sáčku a každou z nich prozkoumat. takovému postupu se říká sčítání – podívat se na každou z nich. Ve většině případů, kde se používá indukce, není sčítání proveditelné.

Abdukce: Předpokládejme, že máte pozorování nějakého zajímavého jevu, který se vám zdá být zajímavý. Nejste si ihned jisti, co pozorování vysvětluje. Přemýšlíte o všech možných hypotézách, které by mohly pozorování věrohodně vysvětlit. na rozdíl od dedukce je to tvůrčí proces. Aby to dobře fungovalo, musíte o situaci vědět co nejvíce. Vzhledem ke všemu, co víte, vyberete hypotézu, která se jeví jako nejrozumnější a nejpravděpodobnější. vybrali jste zřejmě nejlepší vysvětlení, i když může být chybné. neexistuje žádná záruka. Další ověření vašeho vysvětlení jeobvykle dobrý nápad, pokud je to možné; můžete najít další informace, které by vás mohly přimět přehodnotit váš závěr.

Tento druh uvažování je silnou stránkou Sherlocka Holmese. Conan Doyleův proslulý hypervšímavý detektiv si všímá i velmi drobných stop, které policejnímu inspektorovi obvykle unikají. Holmes tyto indicie kombinuje s obecnými znalostmi, které si o případu vybudoval, aby přišel s nejlepším vysvětlením – kdo je pachatelem! Holmes také vysvětluje, jak byl zločin spáchán.Příjemným zpestřením pro čtenáře je, že často vysvětluje úvahy, které ho dovedly k řešení. Zdá se to jednoduché, když to Holmes vysvětluje…

Dedukce

Matematika je deduktivní věda. Navrhují se axiomy. Nejsou testovány; předpokládá se, že jsou pravdivé. Z axiomů se odvozují věty. Při daných axiomech a pravidlech logiky by stroj mohlprodukovat věty.

Obecné -> Konkrétní

Začněte s obecným pravidlem a odvozujte konkrétní výsledky.

Pokud soubor axiomů produkuje větu a jejínegativitu, nazývá se soubor axiomů NEKONZISTENTNÍ.

Předpokládejme, že máme následující známé podmínky.

• Máme velký pytel kuliček.
• O všech kuličkách v pytli je známo, že jsou bílé.
• Mám náhodný vzorek 20 kuliček vybraných z pytle.

Z nich mohu odvodit, že všechny kuličky ve vzorku jsou bílé, i bez toho, abych se na ně podíval. Tento druh uvažování se nazývá modus ponens (více o něm níže a v poznámkách prof. Fishera).

A co tohle?“

• Máme velký pytel kuliček.
• Všechny kuličky v pytli jsou bílé.
• Mám vzorek 20 kuliček smíšených barev.

Z toho rychle vyvodím, že vzorek nebyl odebrán z pytle bílých kuliček. Tento druh uvažování se nazývá modus tollens (více o něm níže a v poznámkách prof. Fishera).

Deduktivní argumenty

Podívejme se na myšlenku deduktivního uvažování (odvozeno z poznámek prof. Fishera).Zde hovoříme o vytváření argumentu pro nějakou myšlenku nebo závěrna základě souboru premis (faktů, myšlenek atd.) Prof. Fisher poznamenává, že filosofové to obvykle ukazují jako

1. Premise number 12. Premise number 2...------------------------C. Conclusion to be reached

Tato struktura představuje argument.Někdy se zapisuje jako
Premisa 1, Premisa 2, Premisa… => Závěr.
Zkráťme to na sylogismus takto:
P => C (premisy implikují závěr, stejně jako výše)
To jednoduše znamená, že pokud jsou premisy pravdivé, pak je pravdivý i závěr.
„Aby byl argument dobrý, musí mít pravdivé premisy a premisy musí nabízet oporu pro závěr. Nejsilnější možná podpora by poskytovala absolutní záruku, že závěr bude pravdivý (samozřejmě za předpokladu, že premisy jsou pravdivé).“ Nejprve se budeme zabývat tímto druhem podpory, ale pak přejdeme k úvahám i o některých slabších druzích podpory.“ (od prof. Fishera)

Jedním obzvláště užitečným druhem argumentu je deduktivně platný argument. (Často se označuje zkratkou „validní argument“ nebo někdy jako „deduktivní argument“) Deduktivně platné argumenty jsou takové argumenty, u nichž by premisy, pokud by byly pravdivé, byly nejsilnějším možným důkazem toho, že závěr je pravdivý. Tyto argumenty totiž poskytují následující záruku: jsou-li premisy pravdivé, pak musí být pravdivý i závěr.
Argument, který se zdá být deduktivní, ale má premisy, které nepodporují závěr (žádná záruka), je neplatnýargument.
Zopakujme si sylogismus P => C (premisy vedou k závěru).Existují čtyři možná tvrzení, která o něm můžete vyslovit:

1. Všechny premisy jsou pravdivé (P je pravdivé) (úvaha modus ponens)
2. Jedna nebo více premis je nepravdivá (P je nepravdivé -). není P)
3. Závěr je pravdivý (C je pravdivý)
4. Závěr je nepravdivý (C je nepravdivý – není C) (modus tollens argumentace)

Pouze dvě z nich (#1 a #4) představují deduktivně platnou argumentaci.Podívejme se na důvod, a to po jedné volbě.

1. P je pravdivý (P) – Potvrzení antecedentu. Jsou-li všechny premisy pravdivé, musí být pravdivý i závěr. Toto je velmi silný argument. (modus ponens)
2. P je nepravdivý (ne P) – Popření antecedentu. To, že P je nepravdivé, nezaručuje, že C je buď pravdivé, nebo nepravdivé. Mohou existovat i jiné příčiny.
3. C je pravdivý (C) – Potvrzení konsekventu. Pokud je C pravdivé, může to býtz jedné z několika příčin, nikoliv z tohoto konkrétního P.
4. C je nepravdivé (ne C) – Popírání konsekventu. Zde platí, že pokud je C nepravdivé, pakP musí být také nepravdivé. Kdyby bylo P pravdivé, bylo by pravdivé i C. (modus tollens)

Krátce řečeno, #1 a #4 (modus ponens a modus tollens) jsou deduktivně platné, zatímco #2 a #3 nikoliv.
Pokud premisy platí pro věci v reálném světě, je třeba ještě provést test neplatnosti. Existují nejméně tři přístupy.

1. Zjistěte, zda můžete najít scénář, ve kterém jsou premisy pravdivé, ale závěr nepravdivý.
2. Zkuste nahradit podstatné nebo přídavné jméno v argumentu jiným. nahradit všechny případy. Pokud to zjevně neplatí, pak původní argument neplatil.
3. Zobrazte P a C ve Vennově diagramu. pokud to můžete udělat tak, že P je pravdivé, ale C je nepravdivé, je argument neplatný. Tyto diagramy jsme pro vás vytvořili níže.

Nyní si přiblížíme téma Vennových diagramů. Ty mohou být velmi užitečnépři kontrole premis argumentu.

Vennovy diagramy

Vennovy diagramy jsou grafickou metodou znázornění logiky.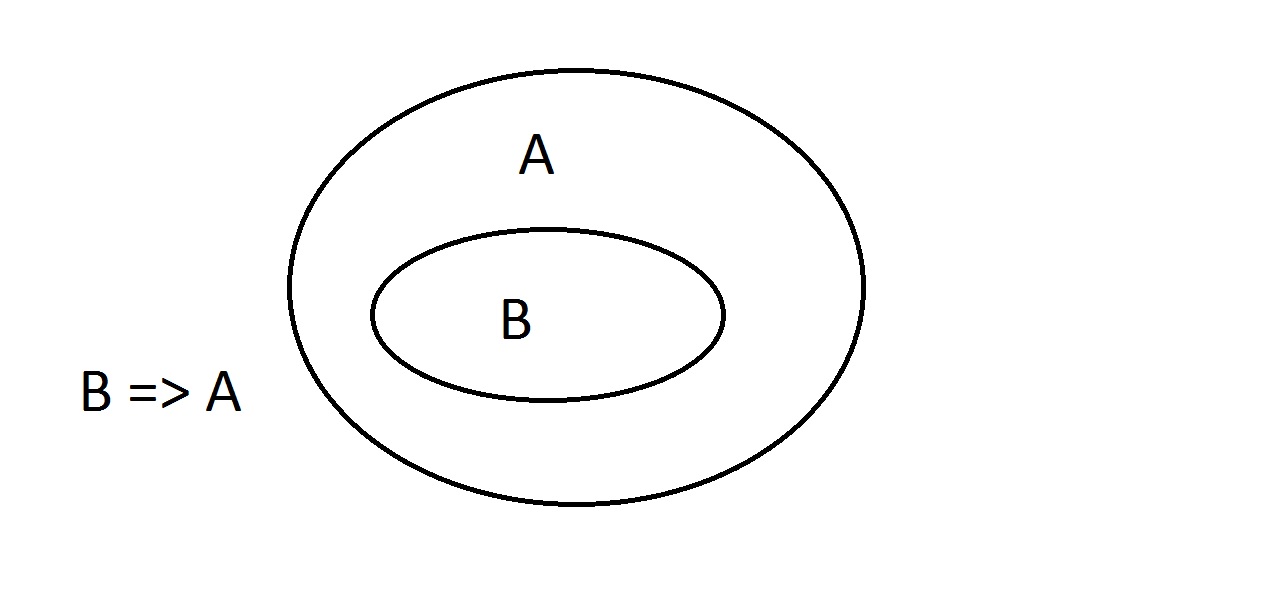
Tento diagram je asi nejjednodušší, jaký dostanete. Vnější ovál obsahuje všechny věci, které mají vlastnost A, zatímco vnitřní ovál obsahuje všechny věci, které mají vlastnost B a také vlastnost A. To je znázorněno jako B=>A, což znamená, že všechny věci, které mají vlastnost B, mají také vlastnost A. Můžete také říci „B implikuje A.“ Pokud je B pravdivé, pak A musí být také. To je výše zmíněná záruka.
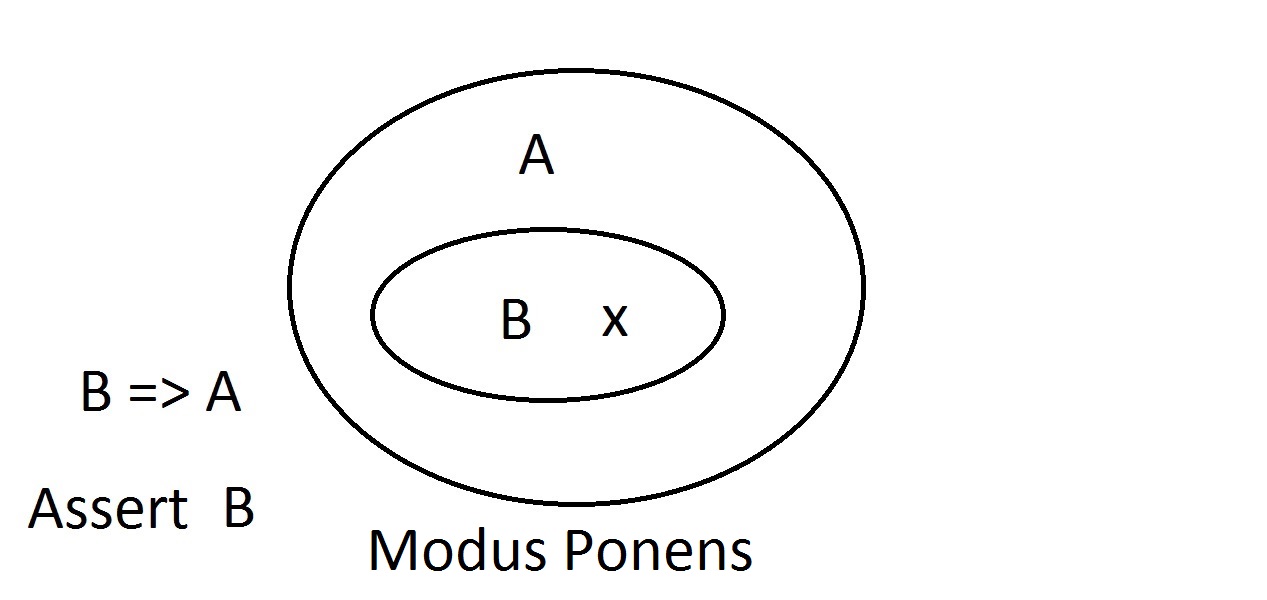Nyní budeme tvrdit, že máme něco s vlastností B. Můžeme s jistotou tvrdit, že to má také vlastnost A. To je modus ponens (tvrzení antecedentu) uvažování. Jakákoli entita s vlastností B zřejmě musí být také v prostoru s vlastností A.
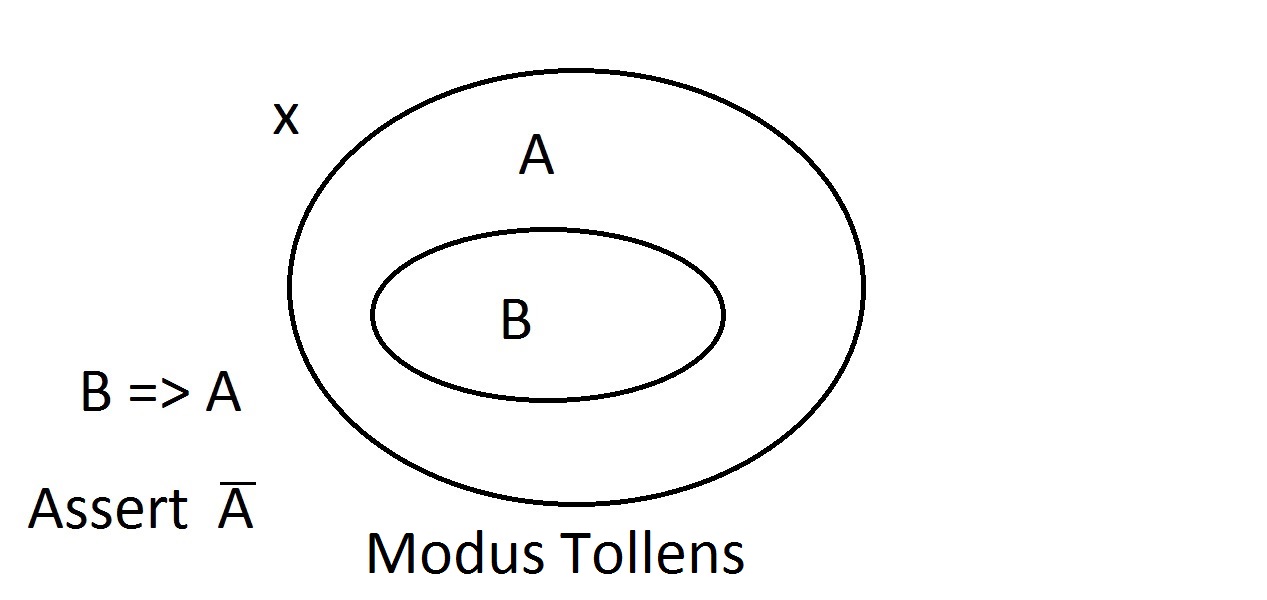Předpokládejme, že nyní budeme tvrdit, že nějaká entita nemá vlastnost A. Vennův diagram ukazuje, že nemůže mít ani vlastnost B. Cokoli mimo prostor vlastnosti Amusí být také mimo prostor vlastnosti B. Toto je modus tollens (popírání důsledků)uvažování a je platné a silné.
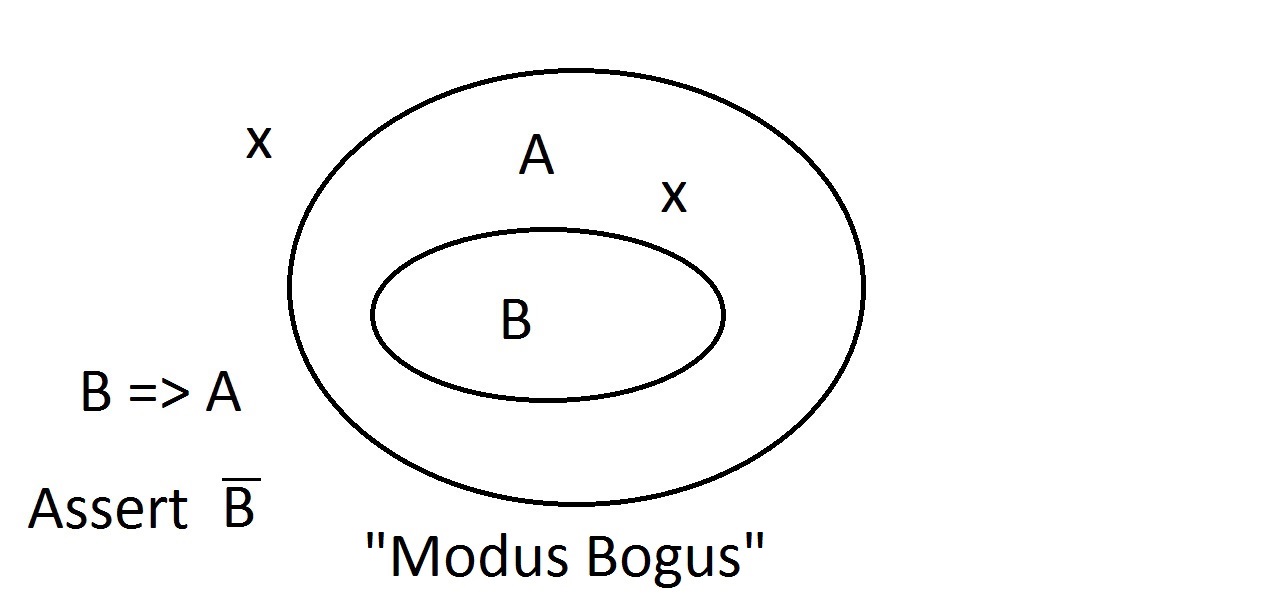Nyní se pokusíme tvrdit, že naše věc nemá vlastnost B. Pohled naVennův diagram ukazuje, jaký je zde problém. Entita nemající vlastnost B může ležet uvnitř prostoru Anebo mimo něj. Tvrzení „nemá B“ nám neříká nic o A. To není platná úvaha, proto jsme ji nazvali Modus Bogus. Je to popírání antecedentu a není platné.
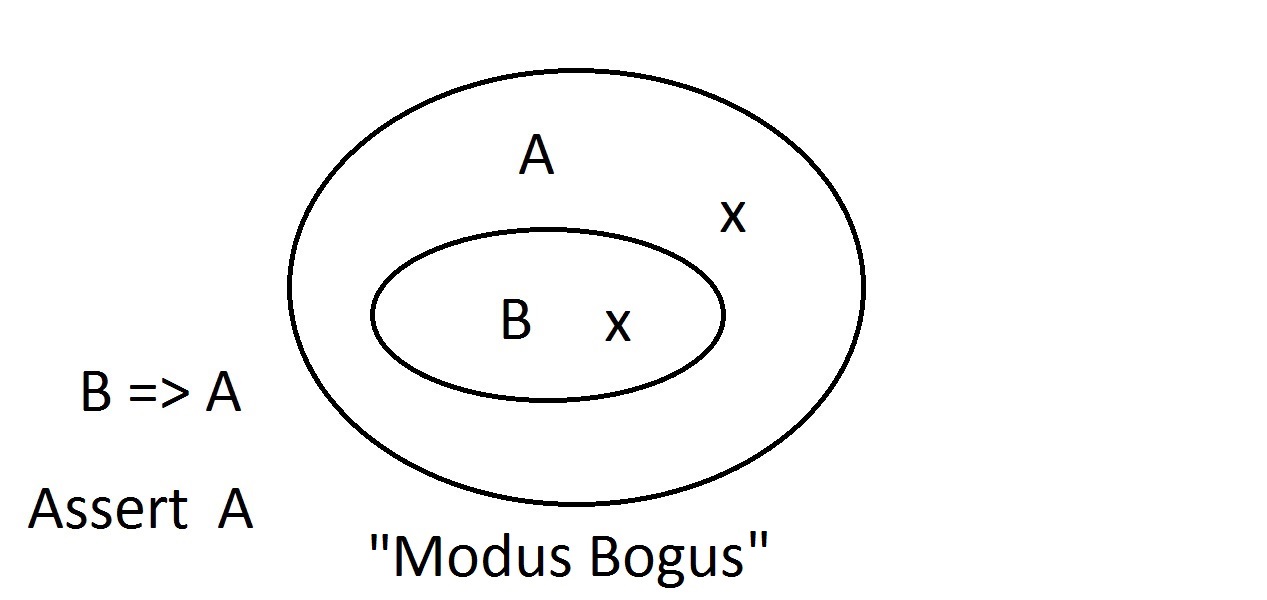Poslední možností je tvrzení, že naše věc má vlastnost A. Vennův diagram ukazuje problém. Entita může ležet kdekoli v prostoru A,buď uvnitř, nebo vně prostoru B. Tvrzení, že věc má vlastnost A, neříká nic o tom, zda má také vlastnost B. To je také Modus Bogus neboli neplatná úvaha. říká se jí tvrzení důsledků.
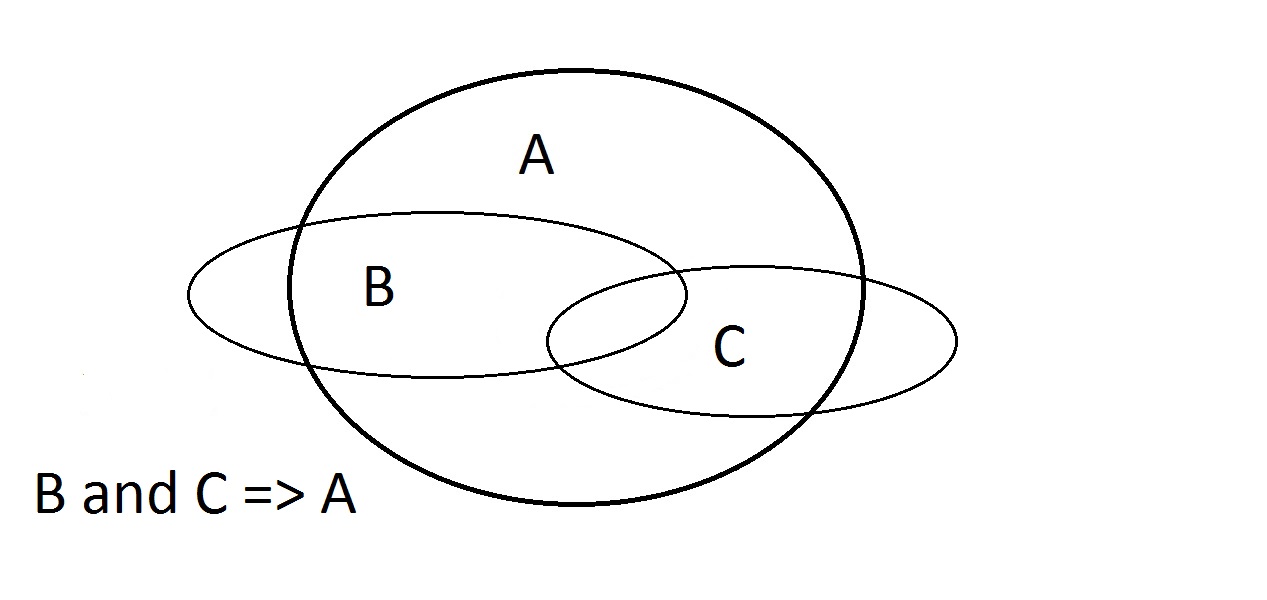Tady máme co do činění s vlastnostmi A, B a C. Zde můžeme zaručit pouze to, že entita, která má B a C, má také A. Všimněte si, že některé z prostorů B a C leží mimo prostor A.

• Ujištění A: Může být kdekoli v A
• Ujištění B: Část B leží mimo A
• Ujištění C: Část C leží mimo A
• Ujištění A a B: Může obsahovat nějaké C; nemusí.
• Potvrzení B a C: Průsečík BC leží celý v A. Tvrzení, že B a C => A funguje.
• Potvrzení A a C: Může zahrnovat některé B; nemusí

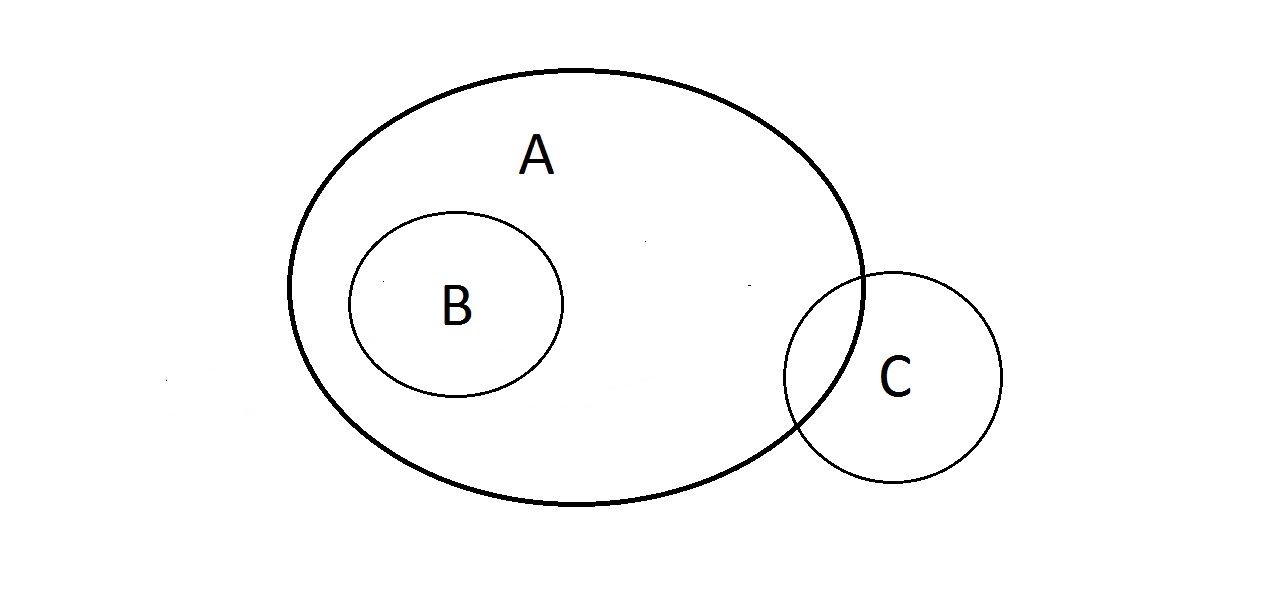
Co s tím můžete dělat? Vlastnosti A a B jsou stejné jako výše, ale co C? Něco, co má vlastnost C, může ležet uvnitř A nebo nemusí. Něco v A může být také v C, nebo nemusí. S vlastností C zde nemůžete nic dělat. Máme však záruku, že něco, co má vlastnost B, má také vlastnost A.

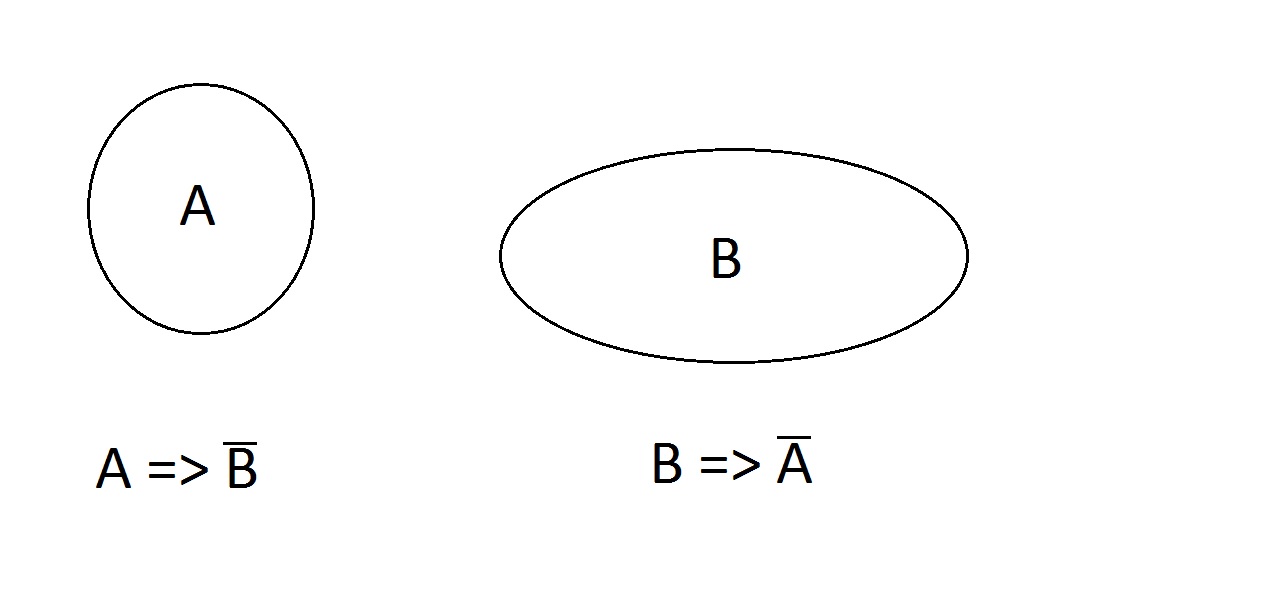
Jak na to. Vlastnosti se vylučují, entita nemůže mít obě současně, může mít žádnou, A nebo B, ale ne AB. Platí tedy výroky A=> není B a B => není A.
Nakonec chceme, aby náš argument byl správný. Aby tomu tak bylo, musí být argumentbeduktivně platný, jak je uvedeno výše, a premisy musí být pravdivé v reálném světě. Toznamená, že všechny zdravé argumenty jsou platné, ale všechny platné argumenty nemusí být nutně zdravé.

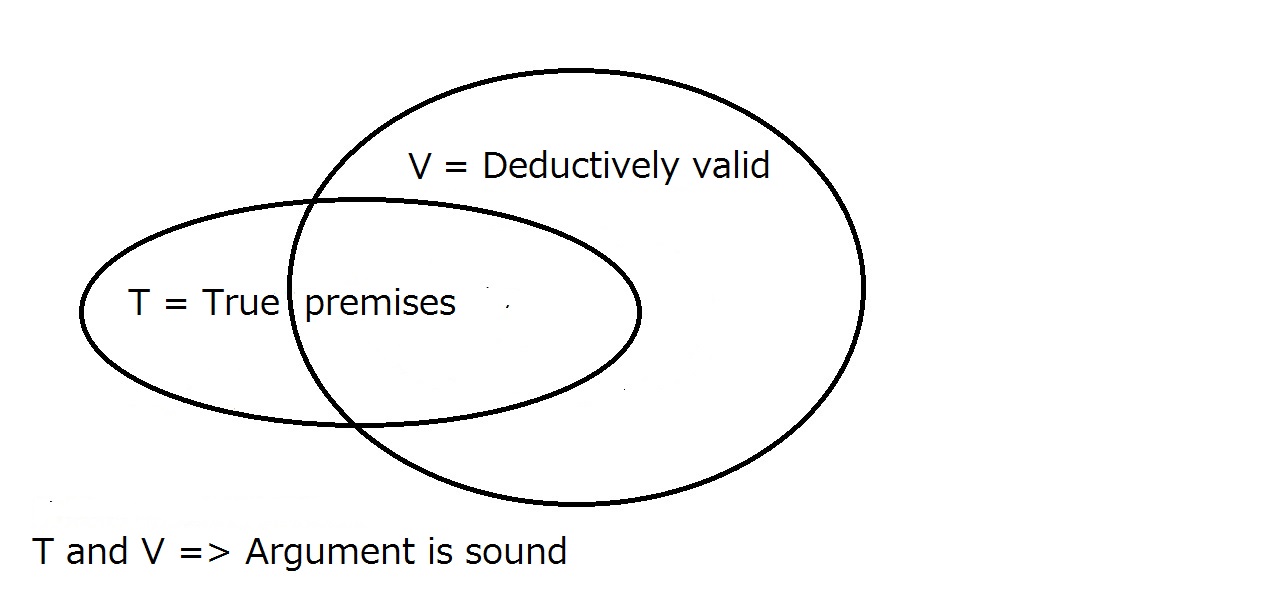
Zdravý argument vyžaduje, aby byl deduktivně platný a měl pravdivé premisy. mít jedno nezaručuje automaticky druhé. Oblast, která je uvnitřT i V, je oblastí zdravých argumentů.

Takto to vidím já. Všichni mě poslouchejte.

Aristoteles (384-322 př. n. l.)

Od http://www.rwe.org/images/aristotle.jpgExperiment?
Samostatně konzistentní?
Jestliže vaše teorie není samostatně konzistentní nebo vaše teorie nesouhlasí s pečlivými experimenty, pak je vaše teorie chybná. Nezáleží na tom, jak je teorie krásná, je špatná.

Galileo Galilei (1564-1642)

Z http://helios.gsfc.nasa.gov/galileo.jpg

např. pátý Euklidův postulát.

(1) Přes libovolné dva různé body lze vést jednu přímku.
(2) Konečnou přímku lze spojitě prodloužit v přímku.
(3) Kružnici lze popsat libovolným bodem jako středem a libovolnou vzdáleností jako poloměrem.
(4) Všechny pravé úhly jsou si rovny.
(5) Přes daný bod lze vést pouze jednu přímku rovnoběžnou s danou přímkou.
Slova „bod“ a „přímka“ nemají žádný vlastní význam.
Mohli bychom zaměnit slova „bod“ a „přímka“ a stále bychom měli pravdivé věty.
Mohli bychom říci
(1) Přes dva libovolné různé blesky lze nakreslit jeden fleem…
Pátý postulát lze změnit dvěma způsoby:
(5) Přes daný bod nelze nakreslit žádnou přímku rovnoběžnou s danou přímkou.
(5) Přes daný bod lze nakreslit mnoho přímek rovnoběžných s danou přímkou.
Oba tyto nové postuláty dávají vzniknout různým SOUČASNÝM geometriím. která z nich je správná? Všechny jsou správné! Která z nich popisuje tento vesmír?
To je FYZIKA!