Professori Fisherin muistiinpanot tästä aiheesta PDF:nä
Professori Fisherin diat tästä aiheesta PDF:nä (salasana vaaditaan)
Professori Sekulan vanhat diat PDF:nä.

Induktio

Huomautus: Filosofit (mm. prof. Fisher) erottavat induktion (jonkin otoksen piirteiden yleistäminen muihin asioihin) abduktiosta (päättely parhaaseen selitykseen), kun taas alla oleva sisältö sekoittaa nämä molemmat yhteen yhden otsikon ”induktio” alle. Kun käydään tätä kurssia professori Fisherin kanssa, on parempi tukeutua hänen muistiinpanoihinsa tai dioihinsa tästä aiheesta kuin alla olevaan sisältöön.

Induktio on prosessi, jossa yritetään selvittää jonkin ilmiön toimintaa tutkimalla näytettä siitä. Työskentelet näytteen avulla, koska ilmiön kaikkien osatekijöiden tutkiminen ei ole mahdollista.Induktio on luova prosessi. Tutkijan on tutkittava huolellisesti näyte ilmiöstä ja muotoiltava sen jälkeen hypoteesi ilmiön selittämiseksi.Tämän jälkeen seuraa tieteellinen prosessi, jossa hypoteesi testataan.Näyttävimpiä tutkimustuloksia saavat ne tutkijat, jotka ovat tarpeeksi luovia keksimään oikeita tutkimuskysymyksiä.

Luonnontieteet (fysiikka, kemia, biologia jne.) ovat induktiivisia.Todisteita kerätään. Tieteellistä menetelmää sovelletaan.Aloitetaan tietyistä tuloksista (otos) ja yritetään arvata yleisiä sääntöjä. Hypoteeseja voidaan vain kumota, ei koskaan todistaa. Jos hypoteesi kestää useiden riippumattomien tutkijoiden toistuvia kokeita, luottamus hypoteesiin kasvaa. Kaikki hypoteesit ovat alustavia; mikä tahansa niistä voidaan kumota huomenna, mutta ”lain” tai ”tosiasian” kumoamiseen tarvitaan erittäin vahvaa todistusaineistoa.

Spesifinen -> Yleinen

Tässä on esimerkki induktiosta: Oletetaan, että olen ottanut 20 kuulaa sattumanvaraisesti suuresta kuulapussista. Jokainen niistä osoittautui valkoiseksi. Se on minunhavaintoni – jokainen ottamani kuula oli valkoinen. Voisin siis muodostaa hypoteesin, että tämä selittyisi, jos kaikki pussissa olevat kuulat olisivat valkoisia. Hypoteesin testaaminen vaatisi lisää näytteenottoa.Saattaa olla, että pussissa on joitain erivärisiä marmorikuulia, eikä ensimmäinen näytteenottoni yksinkertaisesti osunut mihinkään.

Sattumoisin tämä on yksi tapaus, jossa voisimme todistaa hypoteesin todeksi.Voisimme yksinkertaisesti heittää kaikki pussissa olevat marmorikuulat pois ja tutkia jokaisen.Tällaista toimenpidettä sanotaan väestölaskennaksi – tarkastellaan jokaista. Useimmissa tapauksissa, joissa käytetään induktiota, census ei ole toteutettavissa.

Abduktio: Inference to Best Explanation

Tämä on päättelymenetelmä, joka ei ole yhtä tiukka kuin deduktio.Oletetaan, että sinulla on havaintoja mielenkiintoisesta tapahtumasta. Et oleheti varma, mikä selittää havainnot. Ajattelet kaikkia mahdollisia hypoteeseja, jotka voisivat selittää havainnot uskottavasti.Tämä on luova prosessi, toisin kuin deduktio. Jotta tämä toimisi hyvin, sinun on tiedettävä mahdollisimman paljon tilanteesta. Ottaen huomioon kaiken, mitä tiedät, valitset hypoteesin, joka vaikuttaa järkevimmältä ja todennäköisimmältä.Olet valinnut näennäisesti parhaan selityksen, vaikka se voikin olla väärä.Mitään takeita ei ole. Selityksesi tarkempi tarkistaminen on yleensä hyvä ajatus, jos se on mahdollista; saatat löytää lisää tietoa, joka saa sinut harkitsemaan johtopäätöstäsi uudelleen.

Tällainen päättely on Sherlock Holmesin vahvuus. Conan Doylen tunnetusti ylihuomaavainen salapoliisi huomaa hyvin pienetkin vihjeet, jotka poliisitarkastaja yleensä jättää huomaamatta. Holmes yhdistää nämä vihjeet tapauksesta hankkimaansa yleistietoon ja keksii parhaan mahdollisen selityksen – kuka on murhaaja! Hän selittää myös, miten rikos on tehty.Lukijan kannalta mukavana yksityiskohtana Holmes selittää usein perustelut, jotka johtivat hänet ratkaisuun. Se vaikuttaa yksinkertaiselta, kun Holmes selittää sen…

Deduktio

Matematiikka on deduktiivinen tiede. Aksioomeja ehdotetaan. Niitä ei testata; niiden oletetaan olevan totta. Aksioomista johdetaan teoreemoja. Ottaen huomioon aksioomat ja logiikan säännöt kone voisi tuottaa teoreemoja.

Yleinen -> Konkreettinen

Aloitetaan yleisestä säännöstä ja johdetaan konkreettisia tuloksia.

Jos aksioomajoukko tuottaa teoreeman ja sennegatiivisuuden, aksioomajoukkoa sanotaan INKONSISTENTTISEKSI.

Esitettäköön, että meillä on seuraavat tunnetut olosuhteet.

• Meillä on suuri pussi marmorikuulia.
• Kaikkien pussissa olevien marmorien tiedetään olevan valkoisia.
• Minulla on satunnainen 20:n marmorin otos, joka on otettu pussista.

Näistä voin päätellä, että kaikki otoksessa olevat marmorit ovat valkoisia, vaikken edes katsoisikaan niitä. Tällaista päättelyä kutsutaan modus ponensiksi (tästä lisää alla ja professori Fisherin muistiinpanoissa).

Kuinkas tämä?

• Meillä on suuri pussi marmorikuulia.
• Kaikki pussissa olevat kuulat ovat valkoisia.
• Minulla on 20 sekavärisen kuulan näyte.

Tästä päättelen nopeasti, että näyte ei ole otettu pussin valkoisista kuuloista. Tällaista päättelyä kutsutaan modus tollensiksi (tästä lisää alla ja professori Fisherin muistiinpanoissa).

Deduktiiviset argumentit

Katsotaanpa deduktiivisen päättelyn ideaa (johdettu professori Fisherin muistiinpanoista).Tässä puhutaan argumentin laatimisesta jonkin idean tai johtopäätöksen puolesta, joka perustuu joukkoon premissejä (tosiasioita, ideoita jne.) Prof. Fisher huomauttaa, että filosofit esittävät tämän tavallisesti seuraavasti

1. Premise number 12. Premise number 2...------------------------C. Conclusion to be reached

Tämä rakenne muodostaa argumentin.Se kirjoitetaan joskus muotoon
Premissi 1, Premissi 2, Premissi… => Johtopäätös.
Lyhennetään tämä syllogismiksi näin:
P => C (Premissiot implikoivat johtopäätöstä, kuten edellä)
Tämä tarkoittaa yksinkertaisesti sitä, että jos premissiot ovat tosia, myös johtopäätös on tosia.
”Ollakseen hyvä argumentti, argumenteissa on oltava tosia premissejä, ja premisseillä on oltava todellisia lähtökohtia ja niiden on tarjottava tuke johtopäätökselle”. Vahvin mahdollinen tuki antaisi ehdottoman takuun siitä, että johtopäätös on tosi (olettaen tietenkin, että premissiot ovat totta).Tarkastelemme ensin tällaista tukea, mutta siirrymme sitten tarkastelemaan myös joitakin heikompia tukimuotoja.”” (Prof. Fisheriltä)
Yksi erityisen hyödyllinen argumenttilaji on deduktiivisesti pätevä argumentti. (Tästä käytetään usein lyhennettä ”pätevä argumentti” tai joskus ”deduktiivinen argumentti”.) Deduktiivisesti pätevät argumentit ovat argumentteja, joissa premissiot, jos ne olisivat totta, olisivat vahvin mahdollinen todiste siitä, että johtopäätös on tosi. Itse asiassa nämä argumentit antavat seuraavan takuun: jos premissiot ovat totta, myös johtopäätöksen on oltava tosi.
Argumentti, joka vaikuttaa deduktiiviselta, mutta jonka premissiot eivät tue johtopäätöstä (ei takuuta), on epäkelpoargumentti.
Kerrataanpa syllogismi P => C (Premissiot johtavat johtopäätökseen).Tästä voi esittää neljä mahdollista väitettä:

1. Kaikki premissit ovat tosia (P on tosi) (modus ponens päättely)
2. Yksi tai useampi premisseistä on väärä (P on väärä – ei P)
3. Johtopäätös on tosi (C on tosi)
4. Johtopäätös on epätosi (C on epätosi – ei C) (modus tollens – päättely)

Vain kaksi näistä (#1 ja #4) muodostavat deduktiivisesti pätevän päättelyn.Katsotaanpa syytä tähän, yksi valinta kerrallaan.

1. P on tosi (P) – Vahvistetaan antecedentti. Jos kaikki premissiot ovat tosiajohtopäätöksen on oltava tosi. Tämä on hyvin vahva argumentti. (modus ponens)
2. P on epätosi (ei P) – Antecedentin kieltäminen. Se, että P on väärä, ei takaa, että C on joko tosi tai väärä. Voi olla muitakin syitä.
3. C on tosi (C) – Johtopäätöksen vahvistaminen. Jos C on tosi, se voi olla jostain monesta syystä, ei tästä nimenomaisesta P:stä.
4. C on epätosi (ei C) – Johtopäätöksen kieltäminen. Tässä, jos C on väärä niinP:n täytyy myös olla väärä. Jos P olisi tosi, myös C olisi tosi. (modus tollens)

Lyhyesti sanottuna #1 ja #4 (modus ponens ja modus tollens) ovat deduktiivisesti päteviä, kun taas #2 ja #3 eivät ole.
Jos premissiot pätevät asioihin reaalimaailmassa, sinun on silti tehtävä testejä invaliditeetista. Lähestymistapoja on ainakin kolme.

1. Kokeile, löydätkö skenaarion, jossa premissiot ovat tosia, mutta johtopäätös on väärä.
2. Kokeile korvata argumentissa oleva substantiivi tai adjektiivi toisella.Korvaa kaikki tapaukset. Jos tämä ei selvästikään kelpaa, niin alkuperäinenei ollut kelvollinen.
3. Esittele P ja C Venn-diagrammissa.Jos pystyt tekemään tämän niin, että P on tosiMutta C on väärä, väite on virheellinen. Olemme tehneet nämä kaaviot sinulle alla.

Nyt otamme esille Venn-diagrammit. Niistä voi olla suurta hyötyä argumentin premissien tarkistamisessa.

Venn-diagrammit

Venn-diagrammit ovat graafinen tapa esittää logiikkaa.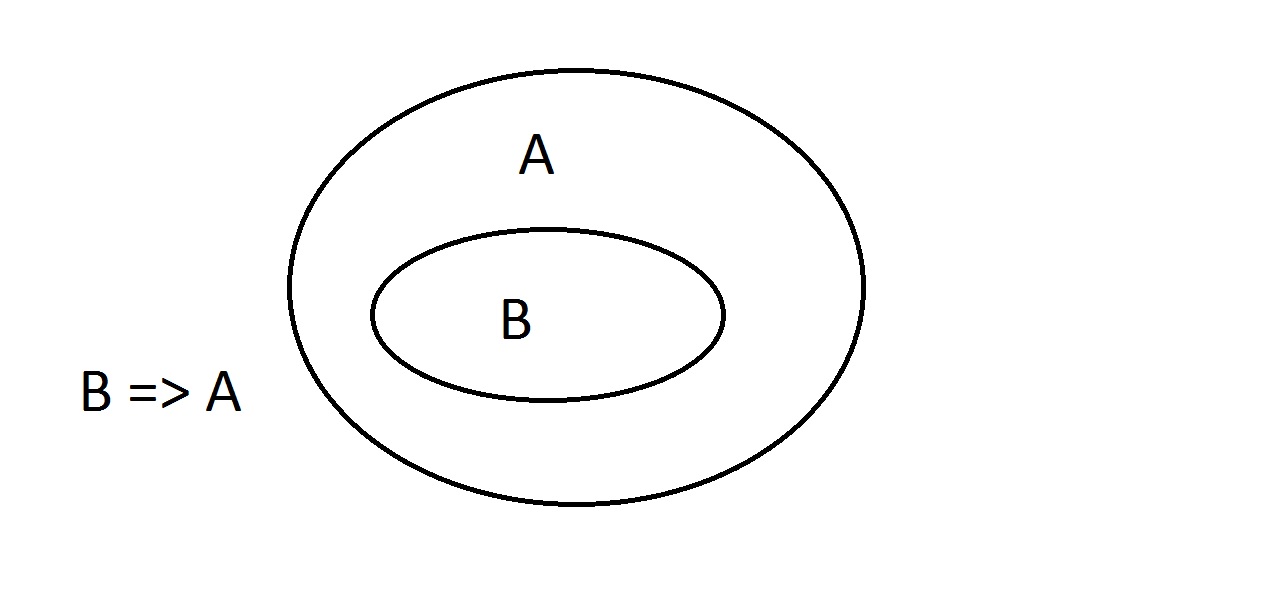
Tämä on suunnilleen yksinkertaisin diagrammi, jonka saat. Ulompi soikio sisältää kaikki asiat, joilla on ominaisuus A, kun taas sisempi soikio sisältää kaikki asiat, joilla on ominaisuus B sekä ominaisuus A. Tämä esitetään muodossa B=>A, mikä tarkoittaa, että kaikilla asioilla, joilla on ominaisuus B, on myös ominaisuus A. Voidaan myös sanoa: ”B implikoi A:n.” Jos B on totta, myös A:n täytyy olla totta. Tämä on edellä mainittu takuu.
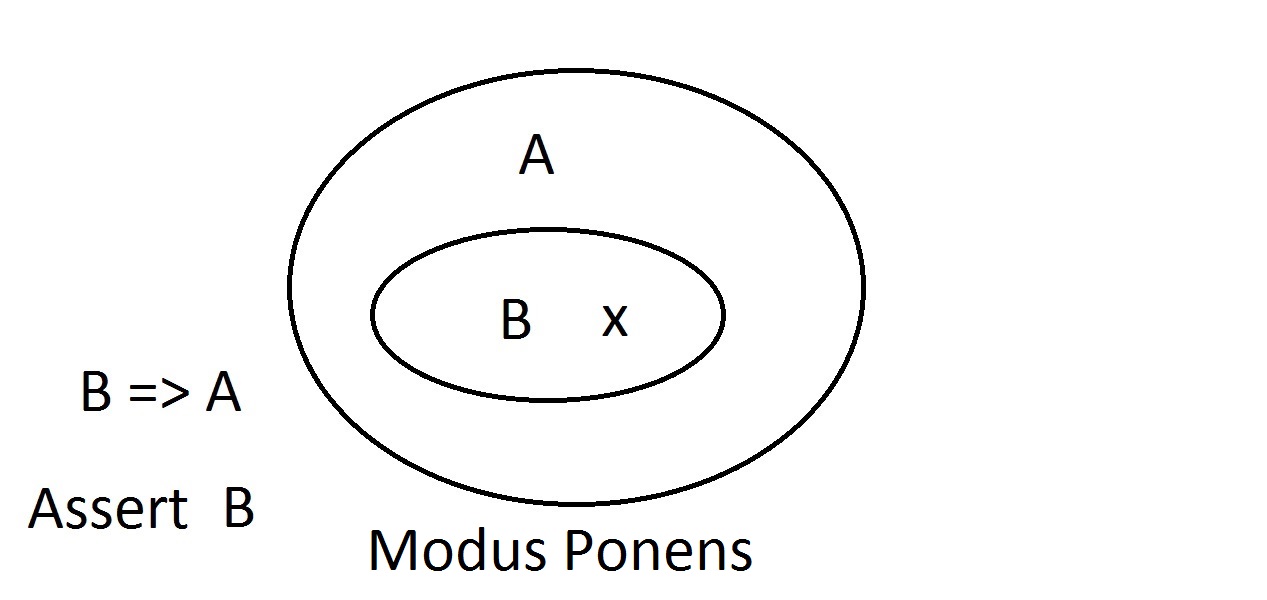Vakuutamme nyt, että meillä on jotain, jolla on ominaisuus B. Voimme varmuudella väittää, että illä on myös ominaisuus A. Tämä on Modus Ponens -ajattelua (antecedentin vahvistaminen). Minkä tahansa olion, jolla on ominaisuus B, on ilmeisesti oltava myös ominaisuus A -avaruudessa.
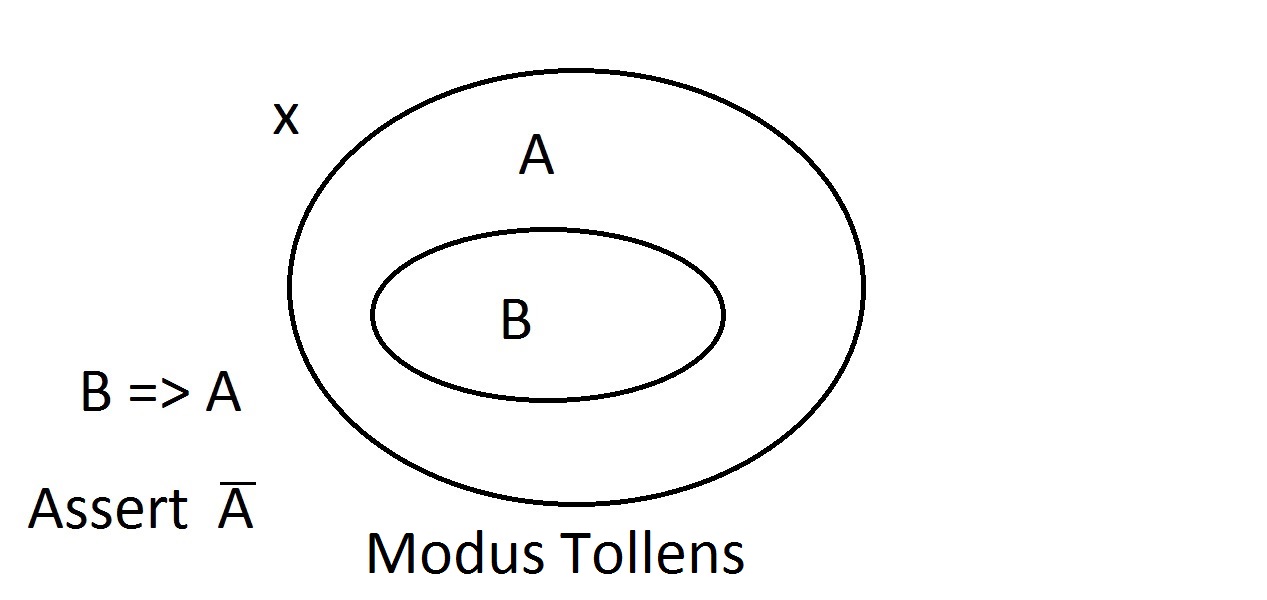Yritetään nyt väittää, että jollakin oliolla ei ole ominaisuutta A. Venn-diagrammi osoittaa, ettei sillä voi olla myöskään ominaisuutta B. Kaiken, mikä on ominaisuus A -avaruuden ulkopuolella, on oltava myös ominaisuus B -avaruuden ulkopuolella. Tämä on Modus Tollens -ajattelua (seurauksen kieltäminen)ja se on pätevää ja vahvaa.
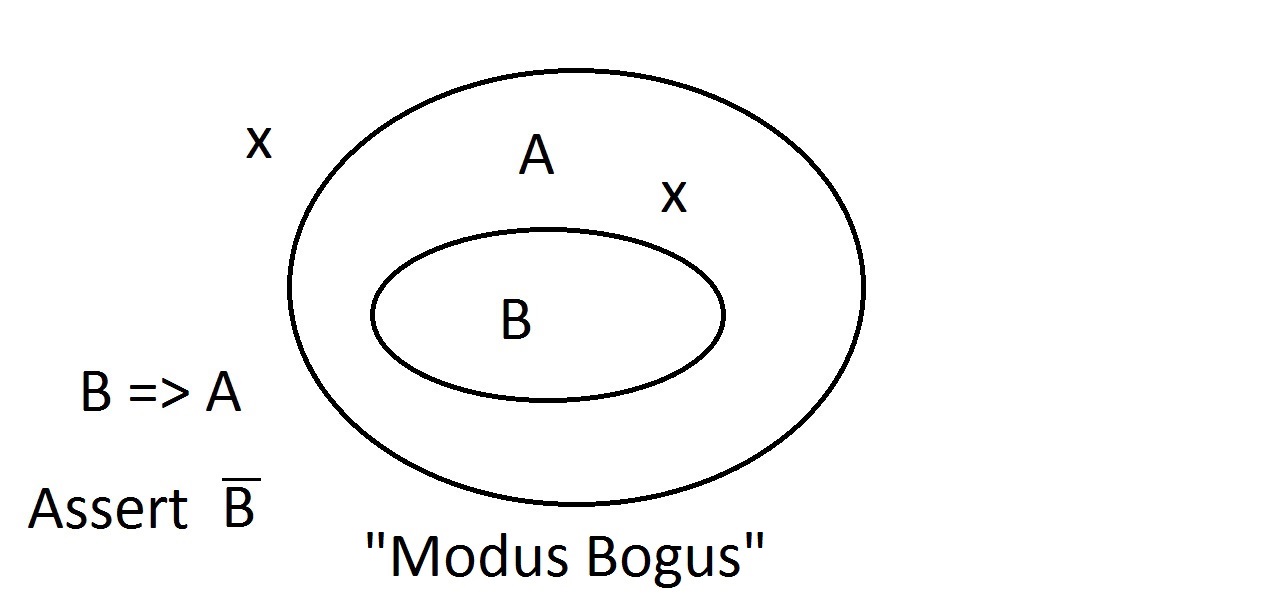Kokeilemme nyt väittää, että oliollamme ei ole ominaisuutta B. VilkaisuVenn-diagrammiin osoittaa tässä olevan ongelman. Olio, jolla ei ole ominaisuutta B, voi sijaita A-avaruuden sisällätai sen ulkopuolella. Väite ”ei B” ei kerro meille mitään A:sta. Tämä ei ole pätevääperustelua, joten kutsuimme sitä Modus Bogukseksi. Se on Antecedentin kieltämistä, eikä se ole pätevä.
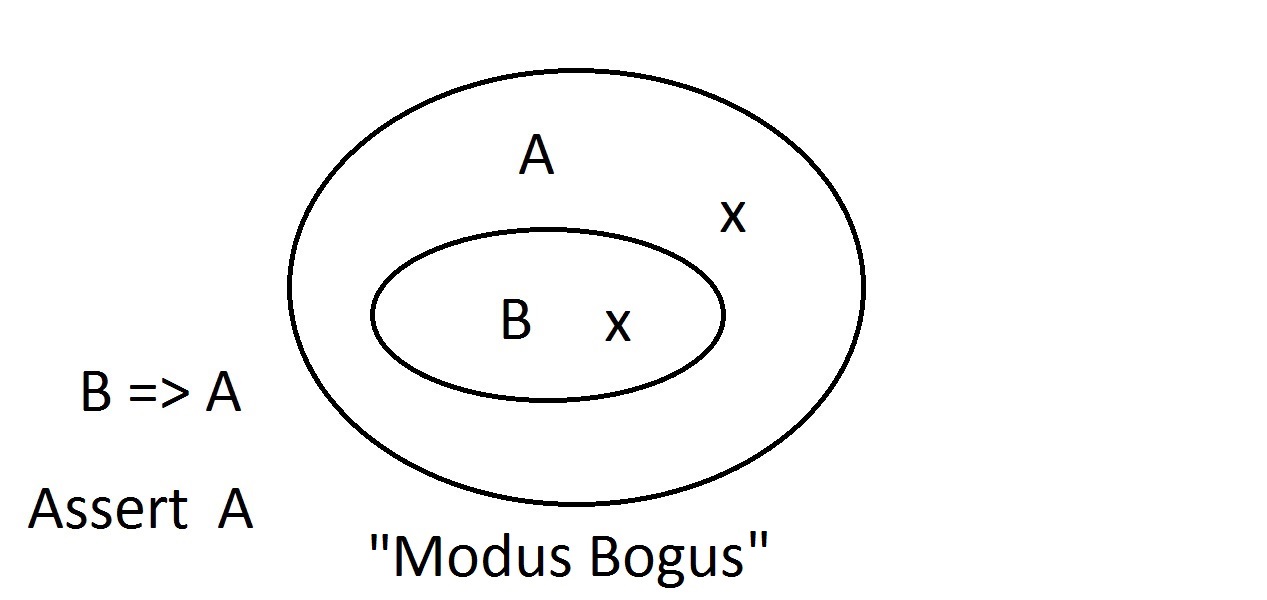Viimeinen mahdollisuus on väittää, että oliollamme on ominaisuus A.Venn-diagrammi osoittaa ongelman. Entiteetti voi sijaita missä tahansa A-avaruudessa,joko B-avaruuden sisällä tai ulkopuolella. Väittämällä, että oliolla on ominaisuus A, emme kerro mitään siitä, onko sillä myös ominaisuus B. Tämä on myös Modus Bogus eli virheellistä päättelyä.sitä kutsutaan seurauksen vahvistamiseksi.
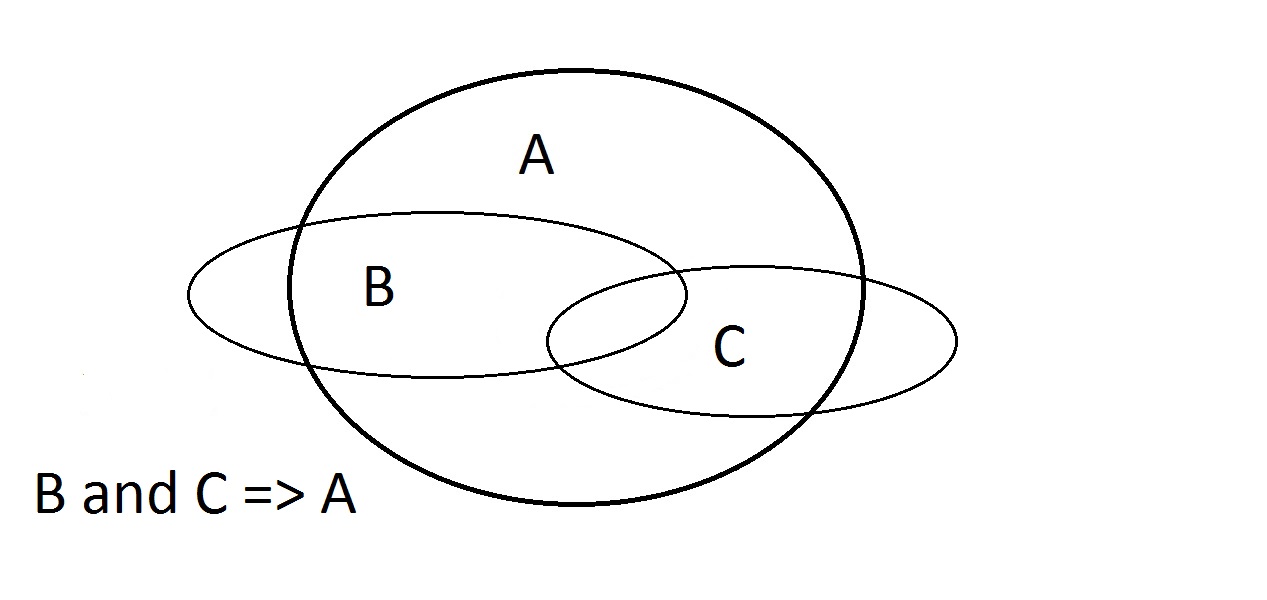Tässä on kyse ominaisuuksista A, B ja C.Tässä voimme taata vain sen, että oliolla, jolla on B ja C, on myös A.Huomaa, että osa B- ja C-avaruuksista sijaitsee A:n ulkopuolella.

• Varmistus A: Voi olla missä tahansa A:ssa
• Varmistus B: Osa B:stä sijaitsee A:n ulkopuolella
• Varmistus C: Osa C:stä sijaitsee A:n ulkopuolella
• Varmistus A ja B: Saattaa sisältää jonkin verran C:tä; saattaa olla, ettei.
• Väite B ja C: Leikkauspiste BC sijaitsee kokonaan A:ssa. Väite B ja C => A toimii.
• Väite A ja C: Saattaa sisältää jonkin verran B:tä; saattaa olla, ettei

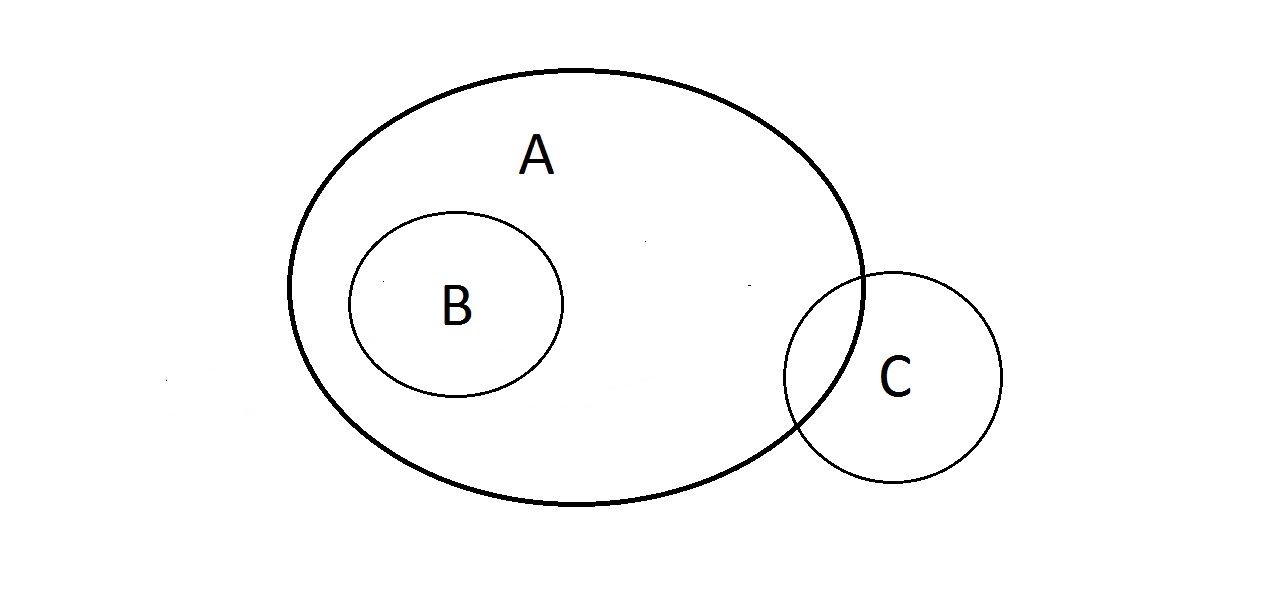
Mitä tällä voi tehdä? Ominaisuudet A ja B ovat kuten edellä, mutta entä C? Jokin, jolla on ominaisuus C, saattaa sijaita A:n sisällä tai sitten ei. Jokin, joka on A:ssa, saattaa olla myös C:ssä tai sitten ei. C:lle ei voi tehdä mitään. Meillä on kuitenkin takuu siitä, että jollakin, jolla on B, on myös A.

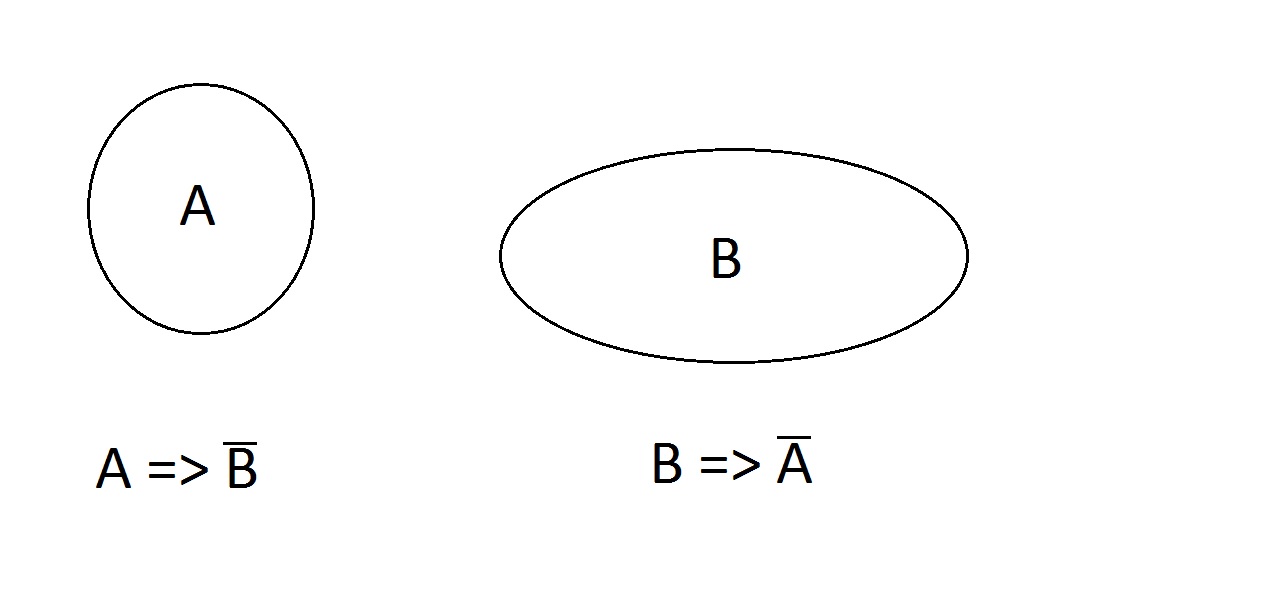
Kuinkas näin. Ominaisuudet ovat poissulkevia; oliolla ei voi olla molempia yhtä aikaa. sillä voi olla ei mitään, A tai B mutta ei AB. Väittämät A=> ei B ja B => ei A ovat päteviä.
Viimeiseksi haluamme, että väitteemme on järkevä. Jotta näin tapahtuisi, argumentin on oltava bededuktiivisesti pätevä kuten edellä ja premissien on oltava totta todellisessa maailmassa. Tämämerkitsee, että kaikki järkevät argumentit ovat päteviä, mutta kaikki pätevät argumentit eivät välttämättä ole järkeviä.

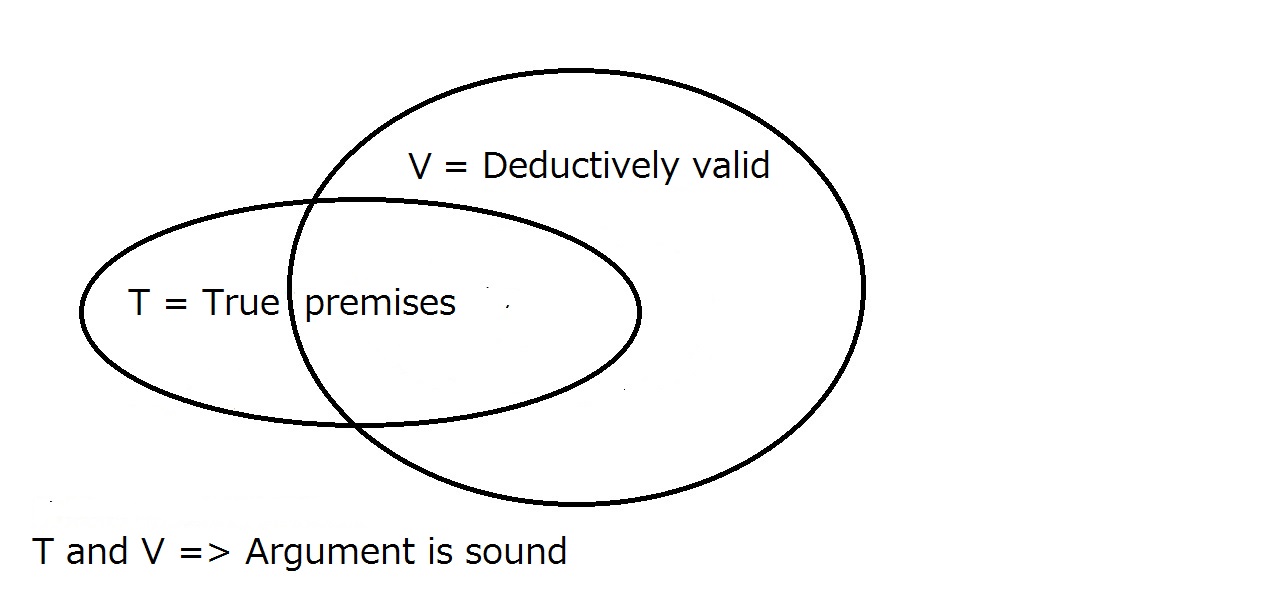
Hyvä argumentti edellyttää, että se on deduktiivisesti pätevä ja että sillä on tosia premissejä.Se, että toinen on olemassa, ei automaattisesti takaa toista. Alue, joka on sekä T:n että V:n sisällä, on äänekkäiden argumenttien alue.

Näin minä sen näen. Kuunnelkaa kaikki minua.

Aristoteles (384-322 eKr.)

Lähteestä http://www.rwe.org/images/aristotle.jpgExperiment?
Self-consistent?
Jos teoriasi ei ole itseään johdonmukainen tai teoriasi on ristiriidassa varovaisten kokeiden kanssa, teoriasi on väärä. Ei ole väliä kuinkakaunis teoria on; se on väärä.

Galileo Galilei (1564-1642)

Lähteestä http://helios.gsfc.nasa.gov/galileo.jpg

esim. Eukleideen viides postulaatti.

(1) Minkä tahansa kahden eri pisteen kautta on mahdollista piirtää yksi viiva.
(2) Äärellinen suora voidaan jatkaa yhtäjaksoisesti suorana.
(3) Ympyrä voidaan kuvata siten, että sen keskipisteenä on mikä tahansa piste ja säteenä mikä tahansa etäisyys.
(4) Kaikki suorat kulmat ovat yhtä suuret.
(5) Tietyn pisteen kautta voidaan piirtää vain yksi yhdensuuntainen suora.
Sanoilla ”piste” ja ”viiva” ei ole mitään varsinaista merkitystä.
Voidaan vaihtaa sanat ”piste” ja ”viiva” keskenään ja saada silti oikeat lauseet.
Voidaan sanoa
(1) Minkä tahansa kahden erilaisen räpylän kautta on mahdollista piirtää yksi fleem…
Viides postulaatti voidaan muuttaa kahdella tavalla:
(5) Tietyn pisteen kautta ei voida piirtää yhtään suoraa yhdensuuntaista suoraa.
(5) Tietyn pisteen kautta voidaan piirtää monta suoraa yhdensuuntaista suoraa.
Kumpikin näistä uusista postulaateista synnyttää erilaiset KONSISTENTTISET geometriat.kumpi on oikein? Ne kaikki ovat! Kumpi niistä kuvaa tätä maailmankaikkeutta?Se on FYSIIKKA!