Notes du professeur Fisher sur ce sujet en PDF
Diapositives du professeur Fisher sur ce sujet en PDF (mot de passe requis)
Anciennes diapositives du professeur Sekula en PDF.

Induction

Note : Les philosophes (dont le prof. Fisher) distinguent l’induction (généralisation des traits d’un certain échantillon à d’autres choses) de l’abduction (inférence à la meilleure explication), alors que le contenu ci-dessous brouille les deux ensemble sous le seul titre de « induction ». Lorsque vous suivez ce cours avec le professeur Fisher, il est préférable de s’appuyer sur ses notes ou ses diapositives sur ce sujet, plutôt que sur le contenu ci-dessous.

L’induction est un processus qui consiste à essayer de comprendre le fonctionnement d’un certain phénomène en étudiant un échantillon de celui-ci. Vous travaillez avec un échantillon parce qu’il n’est pas possible d’examiner toutes les composantes du phénomène.L’induction est un processus créatif. Le scientifique doit étudier soigneusement un échantillon d’un phénomène, puis formuler une hypothèse pour expliquer le phénomène.Le processus scientifique de test de l’hypothèse suit.Les scientifiques qui obtiennent les résultats de recherche les plus spectaculaires sont ceux qui sont assez créatifs pour penser aux bonnes questions de recherche.

Les sciences naturelles (physique, chimie, biologie, etc.) sont inductives.Les preuves sont collectées. On applique la méthode scientifique.On commence par des résultats spécifiques (un échantillon) et on essaie de deviner les règles générales. Les hypothèses ne peuvent être que réfutées, jamais prouvées. Si une hypothèse résiste à des essais répétés par de nombreux chercheurs indépendants, la confiance dans cette hypothèse augmente. Toutes les hypothèses sont provisoires ; n’importe laquelle pourrait être renversée demain, mais il faut des preuves très solides pour renverser une « loi » ou un « fait ».

Spécifique ->Général

Voici un exemple d’induction : Supposons que j’ai pris 20 billes au hasard dans un grand sac de billes. Chacune d’entre elles s’est avérée être blanche. C’est mon observation – chaque bille que j’ai prise était blanche. Je pourrais donc formuler l’hypothèse que cela s’expliquerait si toutes les billes du sac étaient blanches. Un échantillonnage supplémentaire serait nécessaire pour vérifier l’hypothèse.Il se pourrait qu’il y ait des billes de couleurs variées dans le sac et que mon premier échantillon n’en ait tout simplement pas touché.

Incidemment, c’est un cas où nous pourrions prouver que l’hypothèse est vraie.Nous pourrions simplement jeter toutes les billes du sac et examiner chacune d’entre elles.Une telle procédure s’appelle un recensement – regarder chacune d’entre elles. Dans la plupart des cas où l’induction est utilisée, un recensement n’est pas réalisable.

Abduction : Inférence à la meilleure explication

C’est une méthode de raisonnement qui n’est pas rigoureuse comme la Déduction.Supposons que vous ayez des observations d’une occurrence intéressante. Vous n’êtes pas immédiatement sûr de ce qui explique ces observations. Vous réfléchissez à toutes les hypothèses possibles qui pourraient expliquer les observations de façon plausible.C’est un processus créatif, contrairement à la déduction. Pour que cela fonctionne bien, vous devez en savoir le plus possible sur la situation. Compte tenu de tout ce que vous savez, vous choisissez l’hypothèse qui semble la plus raisonnable et la plus probable. Vous avez choisi la meilleure explication apparente, même si elle peut être fausse. Il n’y a aucune garantie. Une vérification plus approfondie de votre explication est généralement une bonne idée si elle est possible ; vous pourriez trouver d’autres informations qui pourraient vous faire reconsidérer votre conclusion.

Ce type de raisonnement est le point fort de Sherlock Holmes. Le célèbre détective hyper-observateur de Conan Doyle remarque même des indices minuscules qui échappent généralement à l’inspecteur de police. Holmes combine ces indices avec les connaissances générales qu’il a acquises sur l’affaire pour trouver la meilleure explication – le coupable ! Il explique également comment le crime a été commis et, ce qui est agréable pour le lecteur, Holmes explique souvent le raisonnement qui l’a conduit à la solution. Cela semble simple quand Holmes l’explique…

Déduction

Les mathématiques sont une science déductive. Des axiomes sont proposés. Elles ne sont pas testées ; elles sont supposées vraies. Les théorèmes sont déduits des axiomes. Étant donné les axiomes et les règles de la logique, une machine pourraitproduire des théorèmes.

Général ->Spécifique

On part de la règle générale et on en déduit des résultats spécifiques.Si l’ensemble des axiomes produit un théorème et sa négation, l’ensemble des axiomes est dit INCONSISTANT.

Supposons que nous ayons les conditions connues suivantes.

• Nous avons un grand sac de billes.
• On sait que toutes les billes du sac sont blanches.
• J’ai un échantillon aléatoire de 20 billes prises dans le sac.

Je peux en déduire que toutes les billes de l’échantillon sont blanches, même sans les regarder. Ce type de raisonnement est appelé modus ponens (plus d’informations à ce sujet ci-dessous et dans les notes du professeur Fisher).

Que diriez-vous de ceci ?

• Nous avons un grand sac de billes.
• Toutes les billes du sac sont blanches.
• J’ai un échantillon de 20 billes de couleurs mélangées.

J’en déduis rapidement que l’échantillon n’a pas été prélevé dans le sac de billes blanches. Ce type de raisonnement est appelé modus tollens (plus d’informations à ce sujet ci-dessous et dans les notes du professeur Fisher).

Arguments déductifs

Regardons l’idée de raisonnement déductif (dérivée des notes du professeur Fisher).Ici, nous parlons de faire un argument pour une certaine idée ou conclusion basée sur un ensemble de prémisses (faits, idées, etc).Prof. Fisher note que les philosophes montrent généralement cela comme

1. Premise number 12. Premise number 2...------------------------C. Conclusion to be reached

Cette structure constitue un argument.Elle s’écrit parfois comme
Premisse 1, Prémisse 2, Prémisse… => Conclusion.
Abrégeons cela en syllogisme comme ceci:
P => C (Les prémisses impliquent la conclusion, comme ci-dessus)
Cela signifie simplement que si les prémisses sont vraies, alors la conclusion est également vraie.
« Pour être bon, un argument doit avoir des prémisses vraies et les prémisses doivent offrir un soutien à la conclusion. Le soutien le plus fort possible fournirait une garantie absolue que la conclusion sera vraie (en présumant, bien sûr, que les prémisses sont vraies).Nous examinerons d’abord ce type de soutien, mais nous passerons ensuite à l’examen de certaines sortes de soutien plus faibles également. » (du professeur Fisher)
Une sorte d’argument particulièrement utile est un argument déductif valide. (Ce terme est souvent abrégé en « argument valide » ou parfois en « argument déductif »)Les arguments déductivement valides sont des arguments dans lesquels les prémisses, si elles étaient vraies, seraient la preuve la plus forte possible que la conclusion est vraie. En effet, ces arguments fournissent la garantie suivante : si les prémisses sont vraies, alors la conclusion doit l’être aussi.
Un argument qui semble être déductif mais dont les prémisses ne soutiennent pas la conclusion (aucune garantie) est un argument invalide.
Reprenons le syllogisme P => C (les prémisses mènent à la conclusion).Il y a quatre affirmations possibles que vous pourriez faire à ce sujet :

1. Toutes les prémisses sont vraies (P est vraie) (raisonnement modus ponens)
2. Une ou plusieurs des prémisses est fausse (P est fausse -. pas P)
3. La conclusion est vraie (C est vrai)
4. La conclusion est fausse (C est faux – pas C) (raisonnement modus tollens)

Seulement deux d’entre eux (#1 et #4) constituent un raisonnement déductif valide.Voyons-en la raison, un choix à la fois.

1. P est vrai (P) – Affirmation de l’antécédent. Si toutes les prémisses sont vraiesla conclusion doit être vraie. C’est un argument très fort. (modus ponens)
2. P est faux (pas P) – Négation de l’antécédent. Le fait que P soit faux ne garantit pas que C soit vrai ou faux. Il pourrait y avoir d’autres causes.
3. C est vrai (C) – Affirmation du conséquent. Si C est vrai, ce pourrait être pour une de plusieurs raisons, pas pour cette P spécifique.
4. C est faux (pas C) – Négation du conséquent. Ici, si C est faux, alors P doit aussi être faux. Si P était vrai, C le serait aussi. (modus tollens)

En bref, #1 et #4 (modus ponens et modus tollens) sont déductivement valides alors que #2 et #3 ne le sont pas.
Si les prémisses s’appliquent à des choses dans le monde réel, vous devez encore faire un test d’invalidité. Il y a au moins trois approches.

1. Voyez si vous pouvez trouver un scénario dans lequel les prémisses sont vraies mais la conclusion fausse.
2. Tentez de remplacer un nom ou un adjectif dans l’argument par un autre.Remplacez toutes les instances. Si cela n’est évidemment pas valable, alors l’original ne l’était pas.
3. Représentez P et C dans un diagramme de Venn.Si vous pouvez le faire de façon à ce que P soit vraimais que C soit faux, l’argument n’est pas valable. Nous avons fait ces diagrammes pour vous ci-dessous.

Nous abordons maintenant le sujet des diagrammes de Venn. Ceux-ci peuvent être d’une grande utilité pour vérifier les prémisses d’un argument.

Diagrammes de Venn

Les diagrammes de Venn sont une méthode graphique de représentation de la logique.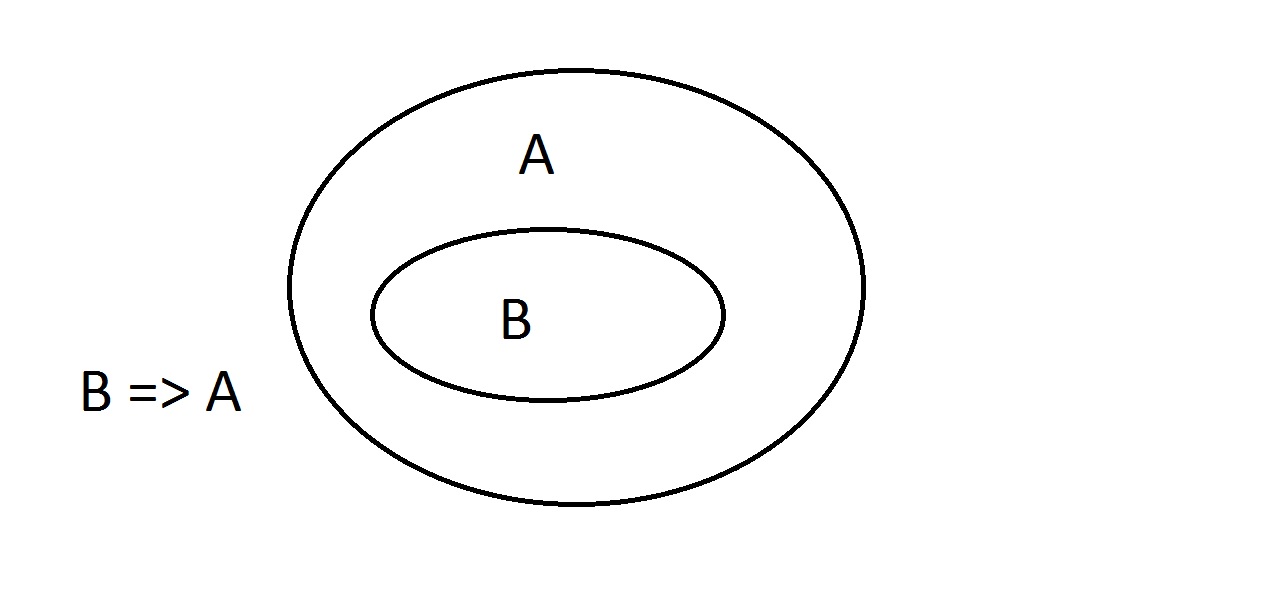
C’est à peu près le diagramme le plus simple que vous aurez. L’ovale extérieur contient toutes les choses ayant la propriété A, tandis que l’ovale intérieur contient toutes les choses ayant la propriété B ainsi que la propriété A.Ceci est montré comme B=>A, ce qui signifie que toutes les choses ayant la propriété B ont aussi la propriété A.Vous pourriez aussi dire « B implique A. « Si B est vrai, alors A doit l’être aussi. C’est la garantie mentionnée ci-dessus.
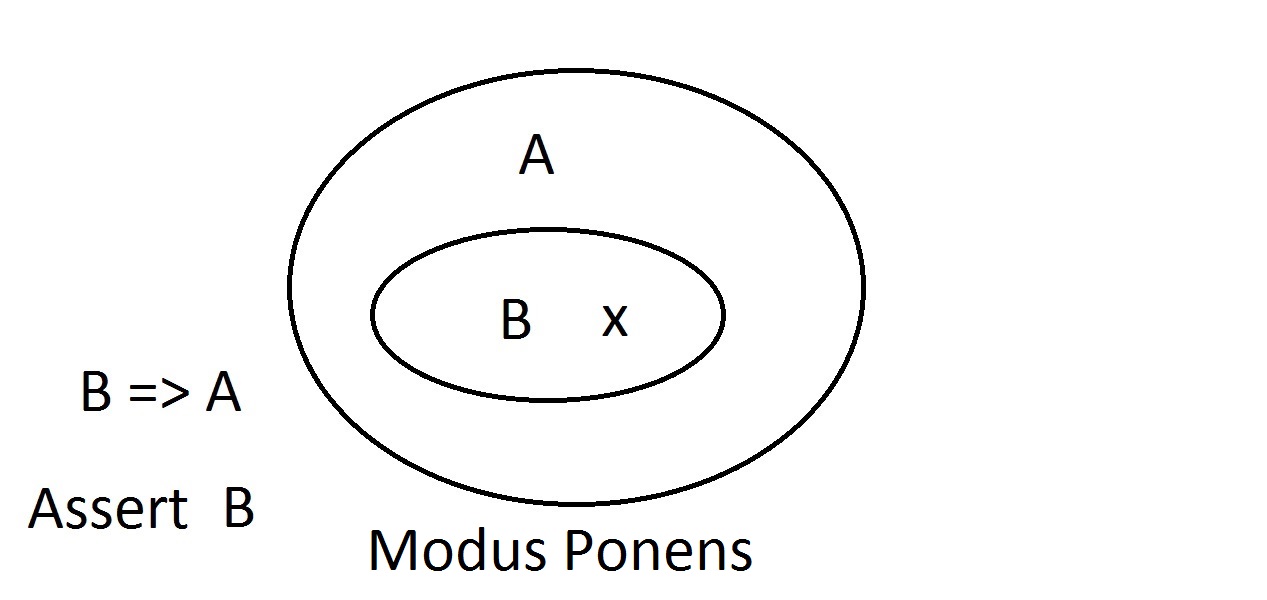Nous allons maintenant affirmer que nous avons quelque chose avec la propriété B. Nous pouvons affirmer avec confiance que ithas la propriété A aussi. C’est le raisonnement Modus Ponens (affirmer l’antécédent). Toute entité ayant la propriété B doit évidemment être aussi dans l’espace de la propriété A.
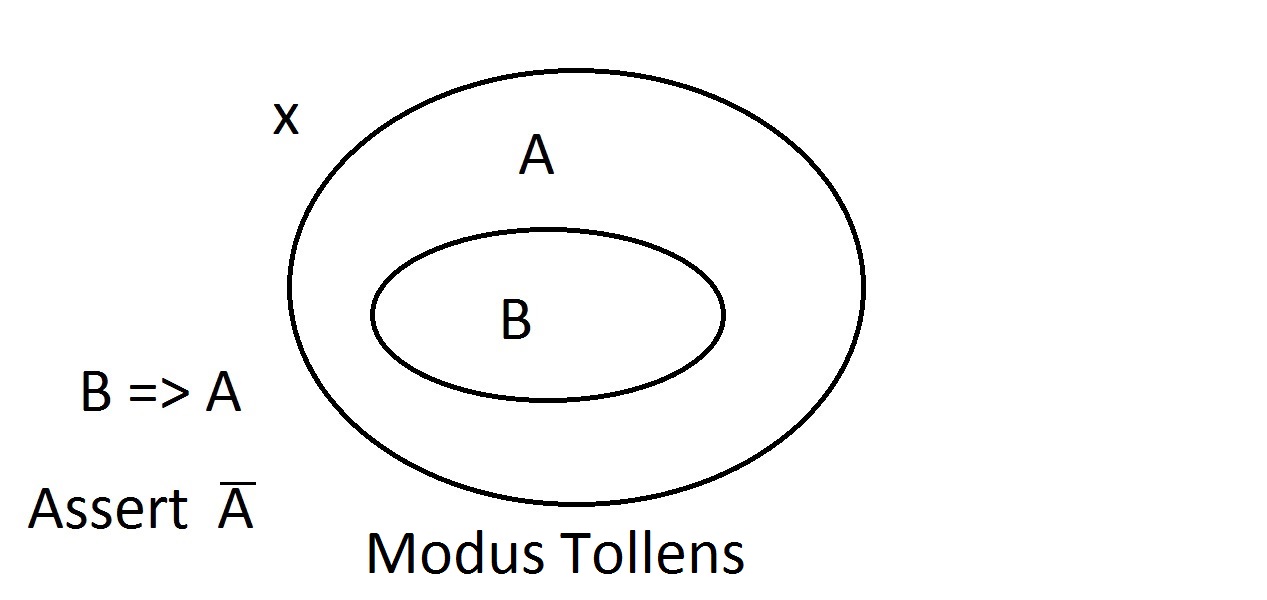Supposons que nous affirmions maintenant qu’une entité n’a pas la propriété A. Le diagramme de Venn montre qu’elle ne peut pas avoir la propriété B non plus. Tout ce qui est en dehors de l’espace de la propriété A doit également être en dehors de l’espace de la propriété B. C’est le raisonnement Modus Tollens (nier le conséquent)et il est valide et fort.
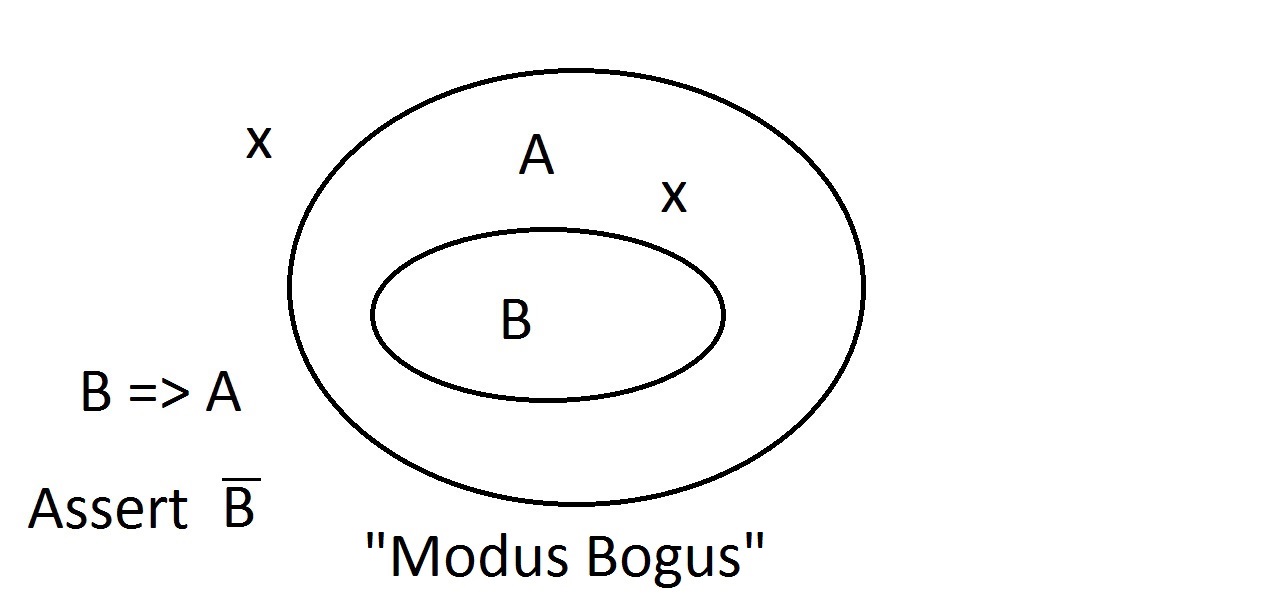Nous allons maintenant essayer d’affirmer que notre chose ne possède pas la propriété B. Un regard sur le diagramme deVenn montre le problème ici. Une entité ne possédant pas la propriété B peut se trouver à l’intérieur de l’espace A ou à l’extérieur de celui-ci. L’affirmation « pas B » ne nous dit rien sur A. Ce n’est pas un raisonnement valide, c’est pourquoi nous l’avons appelé Modus Bogus. C’est nier l’antécédent et ce n’est pas valide.
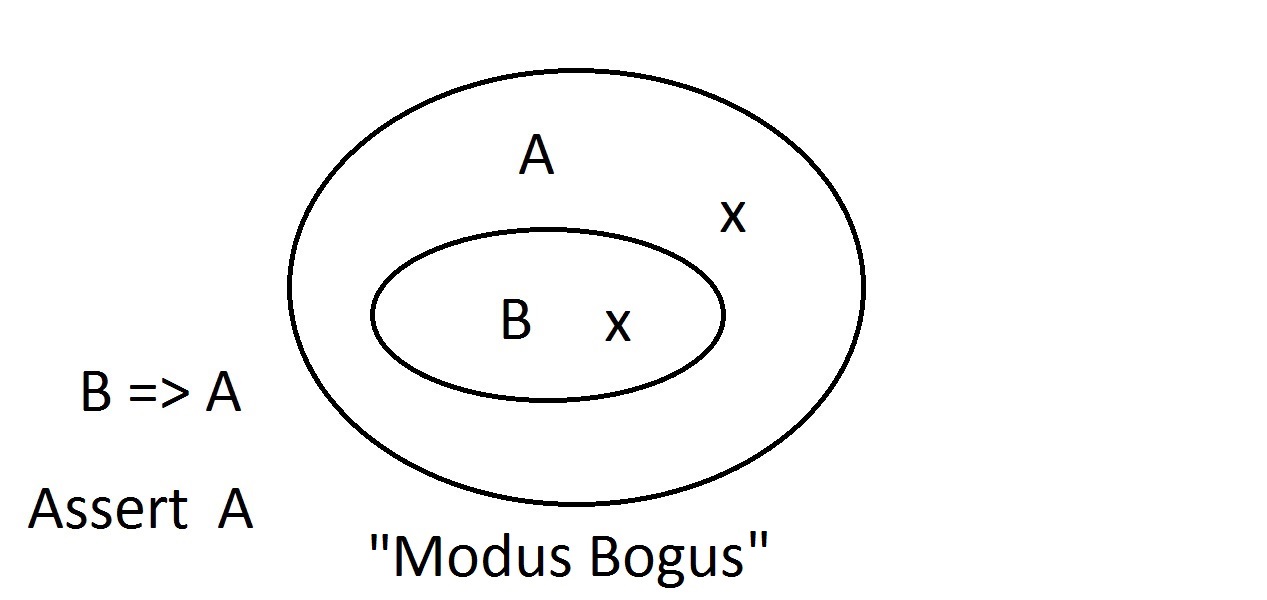La dernière possibilité est d’affirmer que notre chose a la propriété A.Le diagramme de Venn montre le problème. L’entité pourrait se trouver n’importe où dans l’espace A,à l’intérieur ou à l’extérieur de l’espace B. Affirmer que la chose a la propriété Atells ne vous dit rien sur le fait qu’elle a aussi B. C’est aussi le Modus Bogus, ou raisonnement invalide.On appelle cela Affirmer le Conséquent.
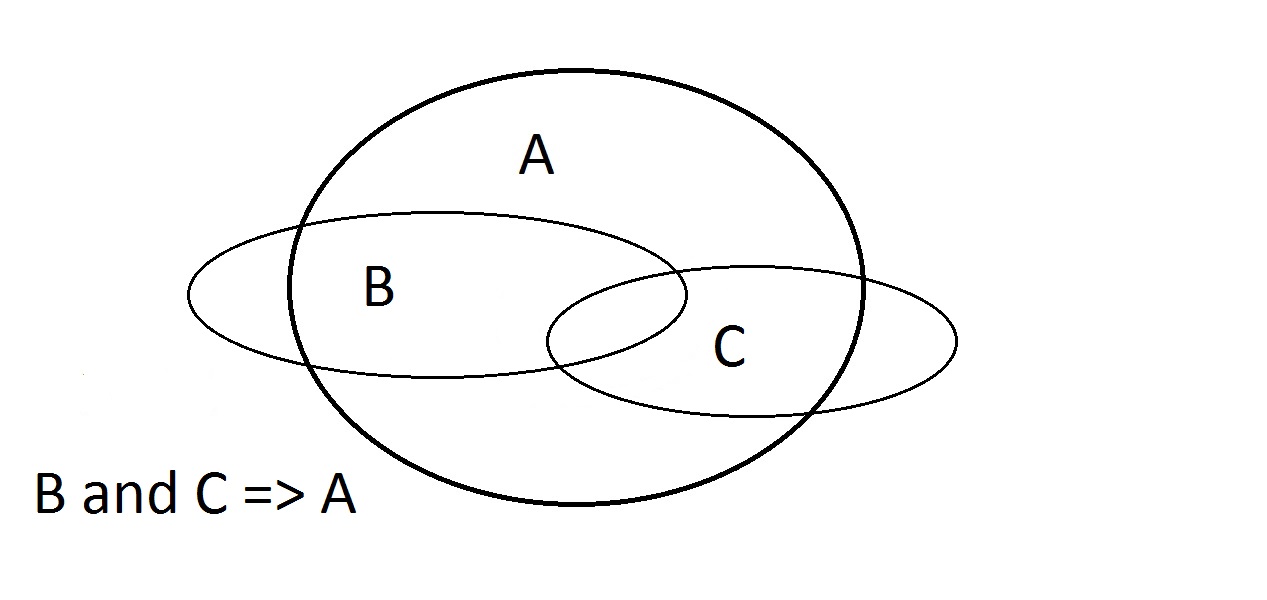Ici, nous avons affaire aux propriétés A, B, et C.Ici, nous pouvons garantir seulement qu’une entité ayant B et C a aussi A.Remarquez que certains des espaces B et C se trouvent à l’extérieur de A.

• Assert A : Pourrait être n’importe où dans A
• Assert B : Une partie de B se trouve en dehors de A
• Assert C : Une partie de C se trouve en dehors de A
• Assert A et B : Pourrait inclure une partie de C ; pourrait ne pas le faire.
• Assert B et C : L’intersection BC se trouve entièrement dans A. Argumenter que B et C => A fonctionne.
• Assert A et C : Pourrait inclure certains B ; pourrait ne pas

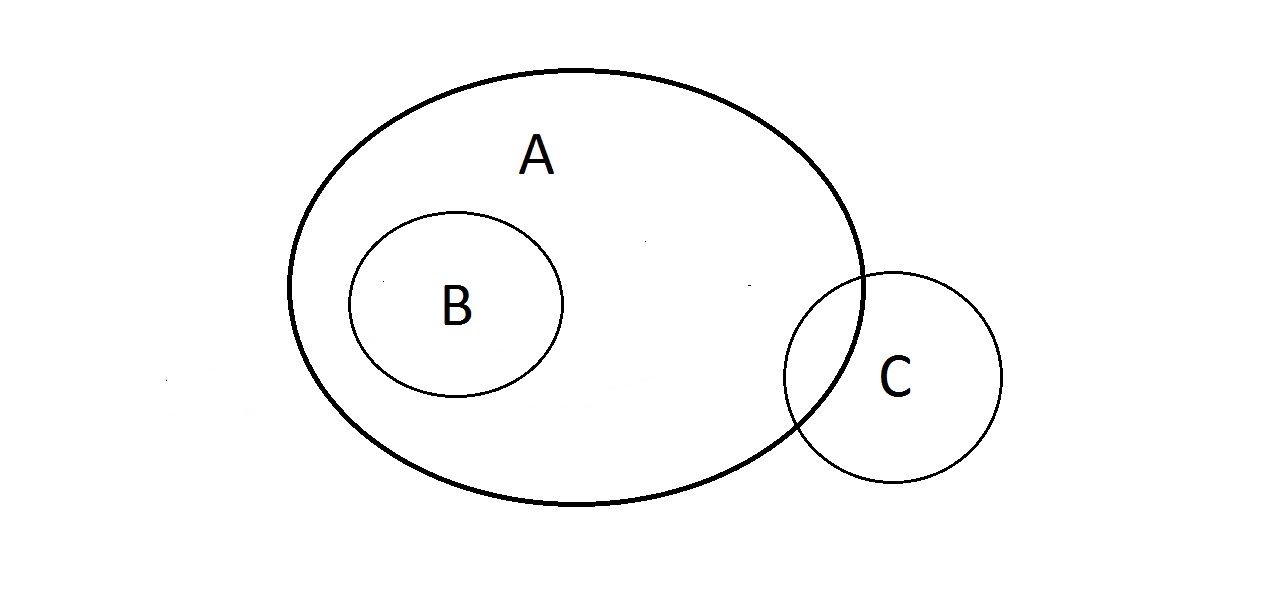
Que pouvez-vous faire avec cela ? Les propriétés A et B sont comme ci-dessus, mais qu’en est-il de C ? Quelque chose ayant la propriété C peut se trouver dans A ou pas. Quelque chose dans A peut aussi être dans C ou non. On ne peut rien faire avec C ici. Nous avons la garantie que quelque chose ayant B a aussi A.

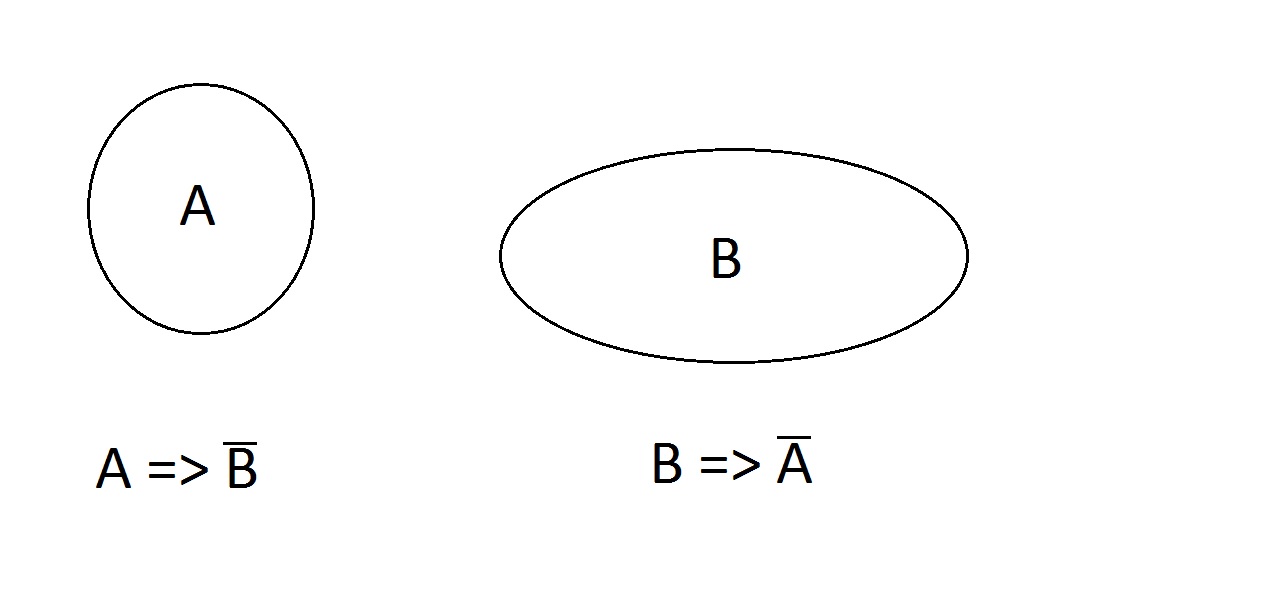
Qu’en est-il de ceci . Les propriétés sont exclusives ; une entité ne peut pas avoir les deux en même temps.Elle peut n’en avoir aucune, A, ou B mais pas AB. Les énoncés A=>non B et B =>non A sont valides.
Enfin, nous voulons que notre argument soit solide. Pour cela, l’argument doit être déductivement valide comme ci-dessus et les prémisses doivent être vraies dans le monde réel. Cela signifie que tous les arguments solides sont valides, mais que tous les arguments valides ne sont pas nécessairement solides.

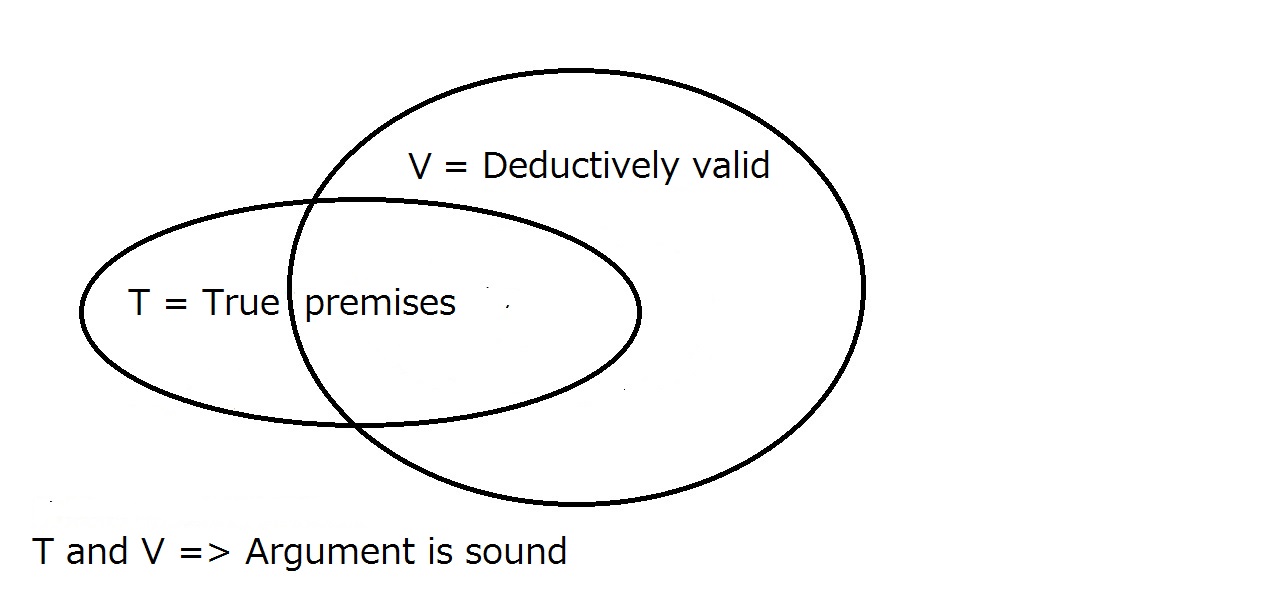
Un argument solide nécessite d’être déductivement valide et d’avoir des prémisses vraies.Avoir l’un ne garantit pas automatiquement l’autre. La région qui est à l’intérieur à la fois deT et de V est la région des arguments solides.

Voici comment je vois les choses. Tout le monde m’écoute.

Aristote (384-322 avant J.-C.)

De http://www.rwe.org/images/aristotle.jpgExperiment?
Self-consistent?
Si votre théorie n’est pas self-consistent, ou si votre théorie est en désaccord avec des expériences soigneuses, alors votre théorie est fausse. Peu importe la beauté de la théorie, elle est fausse.

Galilée (1564-1642)

D’après http://helios.gsfc.nasa.gov/galileo.jpg

par exemple le cinquième postulat d’Euclide.

(1) Par deux points différents quelconques, il est possible de tracer une ligne.
(2) Une droite finie peut être prolongée de façon continue en ligne droite.
(3) Un cercle peut être décrit avec n’importe quel point comme centre et n’importe quelle distance comme rayon.
(4) Tous les angles droits sont égaux.
(5) Par un point donné, on ne peut tracer qu’une seule ligne parallèle à une ligne donnée.
Les mots « point » et « ligne » n’ont pas de signification intrinsèque.
On pourrait échanger « point » et « ligne » et avoir quand même des théorèmes vrais.
On pourrait dire
(1) Par deux blargs différents quelconques, il est possible de tracer une flem…
Le cinquième postulat peut être modifié de deux façons:
(5) Par un point donné, on ne peut tracer aucune ligne parallèle à une ligne donnée.
(5) Par un point donné, on peut tracer de nombreuses lignes parallèles à une ligne donnée.
Ces deux nouveaux postulats donnent lieu à des géométries CONSISTANTES différentes.Laquelle est la bonne ? Elles le sont toutes ! Laquelle décrit cet Univers ? C’est la PHYSIQUE !