Fisher professzor jegyzetei a témáról PDF-ben
Fisher professzor diái a témáról PDF-ben (jelszó szükséges)
Sekula professzor régi diái PDF-ben.

Indukció

Megjegyzés: Filozófusok (köztük prof. Fisher) megkülönböztetik az indukciót (bizonyos minta tulajdonságainak általánosítása más dolgokra) az abdukciótól (következtetés a legjobb magyarázatra), míg az alábbi tartalom a kettőt összemosza egyetlen “indukció” címszó alatt. Ha ezt az órát Fisher professzorral vesszük fel, jobb, ha az ő jegyzeteire vagy diáira támaszkodunk ebben a témában, mint az alábbi tartalomra.

Az indukció egy olyan folyamat, amelynek során megpróbáljuk kitalálni valamilyen jelenség működését egy minta tanulmányozásával. Azért dolgozunk egy mintával, mert a jelenség minden komponensének vizsgálata nem kivitelezhető.Az indukció egy kreatív folyamat. A tudósnak alaposan meg kell vizsgálnia egy jelenség mintáját, majd hipotézist kell megfogalmaznia a jelenség magyarázatára.Ezt követi a hipotézis tesztelésének tudományos folyamata.Azok a tudósok érik el a leglátványosabb kutatási eredményeket, akik elég kreatívak ahhoz, hogy kitalálják a megfelelő kutatási kérdéseket.

A természettudományok (fizika, kémia, biológia stb.) induktívak.Bizonyítékokat gyűjtenek. A tudományos módszert alkalmazzák.Konkrét eredményekből (egy mintából) indulnak ki, és megpróbálják kitalálni az általános szabályokat. A hipotéziseket csak cáfolni lehet, bizonyítani soha. Ha egy hipotézis ellenáll sok független kutató ismételt próbáinak, akkor a hipotézisbe vetett bizalom növekszik. Minden hipotézis előzetes; bármelyik megdönthető holnap, de nagyon erős bizonyítékok szükségesek ahhoz, hogy egy “törvény” vagy “tény” megdönthető legyen.

Specifikus -> Általános

Íme egy példa az indukcióra: Tegyük fel, hogy véletlenszerűen kivettem 20 golyót egy nagy zsák golyóból. Mindegyikről kiderült, hogy fehér. Ez az énmegfigyelésem – minden golyó, amit kivettem, fehér volt. Ezért felállíthatom azt a hipotézist, hogy ez megmagyarázható, ha a zsákban lévő összes golyó fehér volt. A hipotézis teszteléséhez további mintavételre lenne szükség.Lehet, hogy van néhány különböző színű golyó a zsákban, és az első mintám egyszerűen nem talált egyet sem.

Mellesleg ez egy olyan eset, amikor bebizonyíthatjuk, hogy a hipotézis igaz.Egyszerűen kidobhatjuk az összes golyót a zsákban, és megvizsgálhatjuk mindegyiket.Az ilyen eljárást népszámlálásnak nevezik – nézzük meg mindegyiket. A legtöbb esetben, ahol indukciót használunk, az összeírás nem kivitelezhető.

Az indukció: Következtetés a legjobb magyarázatra

Ez egy olyan érvelési módszer, amely nem olyan szigorú, mint a dedukció.Tegyük fel, hogy megfigyeléseink vannak egy érdekes eseményről. Nem vagy azonnal biztos abban, hogy mi magyarázza a megfigyeléseket. Gondolkodsz az összes lehetséges hipotézisen, ami hihetően megmagyarázhatja a megfigyeléseket. ez egy kreatív folyamat, ellentétben a dedukcióval. Ahhoz, hogy ez jól működjön, a lehető legtöbbet kell tudnod a helyzetről. Mindent figyelembe véve, amit tudsz,kiválasztod azt a hipotézist, amely a legésszerűbbnek és legvalószínűbbnek tűnik.A látszólag legjobb magyarázatot választottad, bár lehet, hogy tévedsz.Garancia nincs. A magyarázatod további ellenőrzése általában jó ötlet, ha lehetséges; lehet, hogy több olyan információt találsz, ami miatt újra átgondolhatod a következtetésedet.

Ez a fajta érvelés Sherlock Holmes erőssége. Conan Doyle híresen hiperfigyelmes detektívje olyan apró nyomokat is észrevesz, amelyeket a rendőrfelügyelő általában nem vesz észre. Holmes ezeket a nyomokat kombinálja az ügyről felhalmozott általános ismereteivel, hogy a legjobb magyarázatra jusson – ki a tettes! Azt is megmagyarázza, hogyan történt a bűntény.Az olvasó számára kedves módon Holmes gyakran elmagyarázza, milyen érveléssel jutott el a megoldáshoz. Egyszerűnek tűnik, amikor Holmes elmagyarázza…

Dedukció

A matematika deduktív tudomány. Axiómákat javasolnak. Nem tesztelik őket; igaznak feltételezik őket. A tételeket az axiómákból vezetik le. Az axiómák és a logikai szabályok ismeretében egy gép képes lenne tételeket előállítani.

Általános -> Speciális

Az általános szabályból kiindulva levezetjük a speciális eredményeket.Ha az axiómák halmaza egy tételt és annak tagadását eredményezi, akkor az axiómák halmazát INKONSISTENSnek nevezzük.

Tegyük fel, hogy a következő ismert feltételek állnak fenn.

• Van egy nagy zsáknyi golyó.
• A zsákban lévő összes golyóról tudjuk, hogy fehér.
• Van egy 20 golyóból álló véletlenszerű mintám a zsákból.

Ezekből le tudom következtetni, hogy a mintában lévő összes golyó fehér, anélkül is, hogy megnézném őket. Ezt a fajta következtetést modus ponensnek nevezik (erről bővebben alább és Fisher professzor jegyzeteiben).

Hogyan állunk ezzel?

• Van egy nagy zsáknyi golyónk.
• A zsákban lévő összes golyó fehér.
• Van egy 20 darab vegyes színű golyóból álló mintám.

Ebből gyorsan kikövetkeztetem, hogy a minta nem a fehér golyókból álló zsákból származik. Ezt a fajta érvelést modus tollensnek nevezik (erről bővebben alább és Fisher professzor jegyzeteiben).

Deduktív érvelés

Nézzük meg a deduktív érvelés gondolatát (Fisher professzor jegyzeteiből).Itt arról van szó, hogy valamilyen gondolat vagy következtetés mellett érvelünk egy sor premissza (tény, ötlet stb.) alapján.” Fisher professzor megjegyzi, hogy a filozófusok ezt általában így mutatják be:

1. Premise number 12. Premise number 2...------------------------C. Conclusion to be reached

Ez a szerkezet alkotja az érvelést.Néha így írják le:
1. premissza, 2. premissza, premissza… => következtetés.
Rövidítsük ezt szillogizmusra így:
P => C (a premisszák implikálják a következtetést, mint fentebb)
Ez egyszerűen azt jelenti, hogy ha a premisszák igazak, akkor a következtetés is igaz.
“Ahhoz, hogy egy érv jó legyen, igaz premisszákkal kell rendelkeznie, és a premisszáknak támogatást kell nyújtaniuk a következtetéshez. A legerősebb lehetséges alátámasztás abszolút garanciát nyújtana arra, hogy a következtetés igaz lesz (természetesen feltételezve, hogy a premisszák igazak).” Először ezt a fajta alátámasztást fogjuk megvizsgálni, de aztán áttérünk néhány gyengébb fajta alátámasztás vizsgálatára is.” (Fisher professzortól)
Az egyik különösen hasznos érvfajta a deduktívan érvényes érv. (Ezt gyakran “érvényes érvként” vagy néha “deduktív érvként” rövidítik.) A deduktívan érvényes érvek olyan érvek, amelyekben a premisszák, ha igazak lennének, a lehető legerősebb bizonyítékai lennének annak, hogy a következtetés igaz. Valójában ezek az érvek a következő garanciát nyújtják: ha a premisszák igazak, akkor a következtetésnek is igaznak kell lennie.
Az olyan érv, amely deduktívnak tűnik, de olyan premisszák vannak benne, amelyek nem támasztják alá a következtetést (nincs garancia), érvénytelen érv.
Ismételjük meg a P => C szillogizmust (Premisszák vezetnek a következtetéshez).Erről négy lehetséges állítást tehetünk:

1. A premisszák mindegyike igaz (P igaz) (modus ponens érvelés)
2. A premisszák közül egy vagy több hamis (P hamis – nem P)
3. A következtetés igaz (C igaz)
4. A következtetés hamis (C hamis – nem C) (modus tollens érvelés)

Ezek közül csak kettő (#1 és #4) képez deduktívan érvényes érvelést.Nézzük meg ennek okát, választásonként egyenként.

1. P igaz (P) – Az antecedens megerősítése. Ha minden premissza igaza következtetésnek igaznak kell lennie. Ez egy nagyon erős érv. (modus ponens)
2. P hamis (nem P) – Az antecedens tagadása. Az, hogy P hamis, nem garantálja, hogy C vagy igaz vagy hamis. Lehetnek más okok is.
3. C igaz (C) – A következmény megerősítése. Ha C igaz, akkor az több ok közül valamelyik lehet, nem ez a konkrét P.
4. C hamis (nem C) – A következmény tagadása. Itt, ha C hamis, akkorP-nek is hamisnak kell lennie. Ha P igaz lenne, akkor C is az lenne. (modus tollens)

Röviden, az #1 és #4 (modus ponens és modus tollens) deduktívan érvényesek, míg a #2 és #3 nem.
Ha a premisszák a valós világ dolgaira vonatkoznak, akkor is meg kell tennünk egy érvénytelenségi tesztet. Legalább három megközelítés létezik.

1. Vizsgáld meg, hogy találsz-e olyan forgatókönyvet, amelyben a premisszák igazak, de a konklúzió hamis.
2. Próbálj meg egy főnevet vagy melléknevet egy másikkal helyettesíteni az érvelésben.Cseréld ki az összes esetet. Ha ez nyilvánvalóan nem érvényes, akkor az eredeti nem volt érvényes.
3. Elképezd P-t és C-t egy Venn-diagramban.Ha ezt úgy tudod megtenni, hogy P igaz, de C hamis, akkor az érv érvénytelen. Ezeket az ábrákat az alábbiakban elkészítettük neked.

Most felhozzuk a Venn-diagramok témáját. Ezek nagy hasznunkra lehetnek egy érv premisszáinak ellenőrzésében.

Venn-diagramok

A Venn-diagramok a logika ábrázolásának grafikus módszere.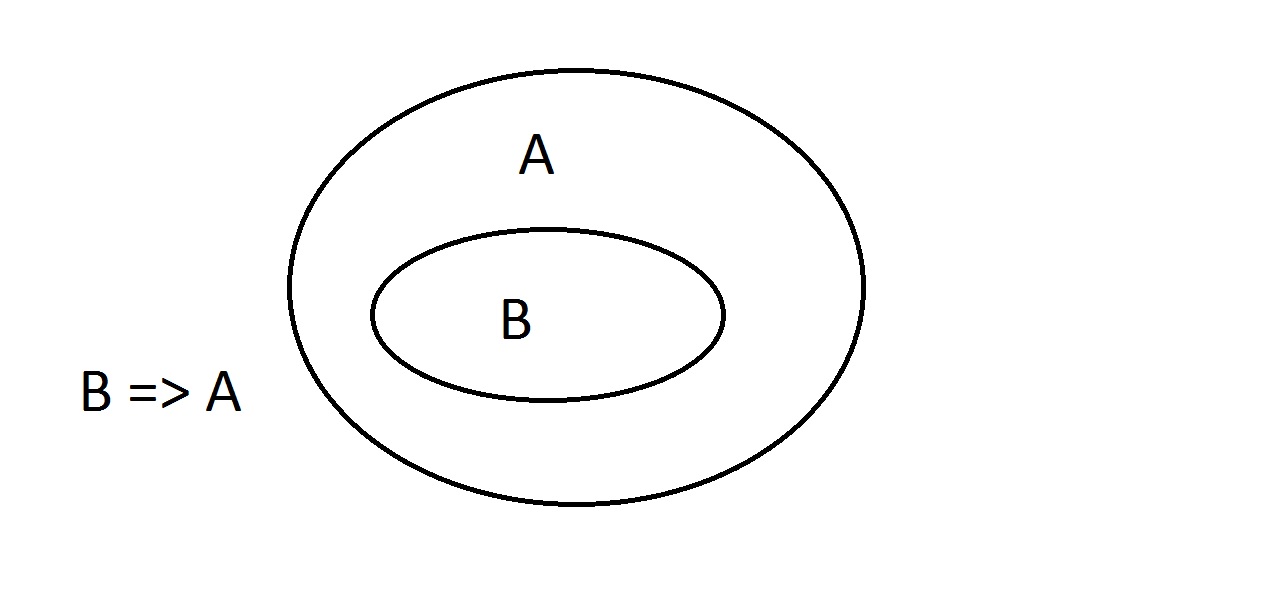
Ez körülbelül a legegyszerűbb diagram, amit kapunk. A külső ovális tartalmazza az összes olyan dolgot, amelynekAtulajdonsága van, míg a belső ovális tartalmazza az összes olyan dolgot, amelynek B tulajdonsága van, valamint A tulajdonsága.Ezt úgy ábrázoljuk, hogy B=>A, ami azt jelenti, hogy minden olyan dolognak, amelynek B tulajdonsága van, A tulajdonsága is van.Azt is mondhatjuk, hogy “B implikálja A-t.” Ha B igaz, akkor A-nak is igaznak kell lennie. Ez a fent említett garancia.
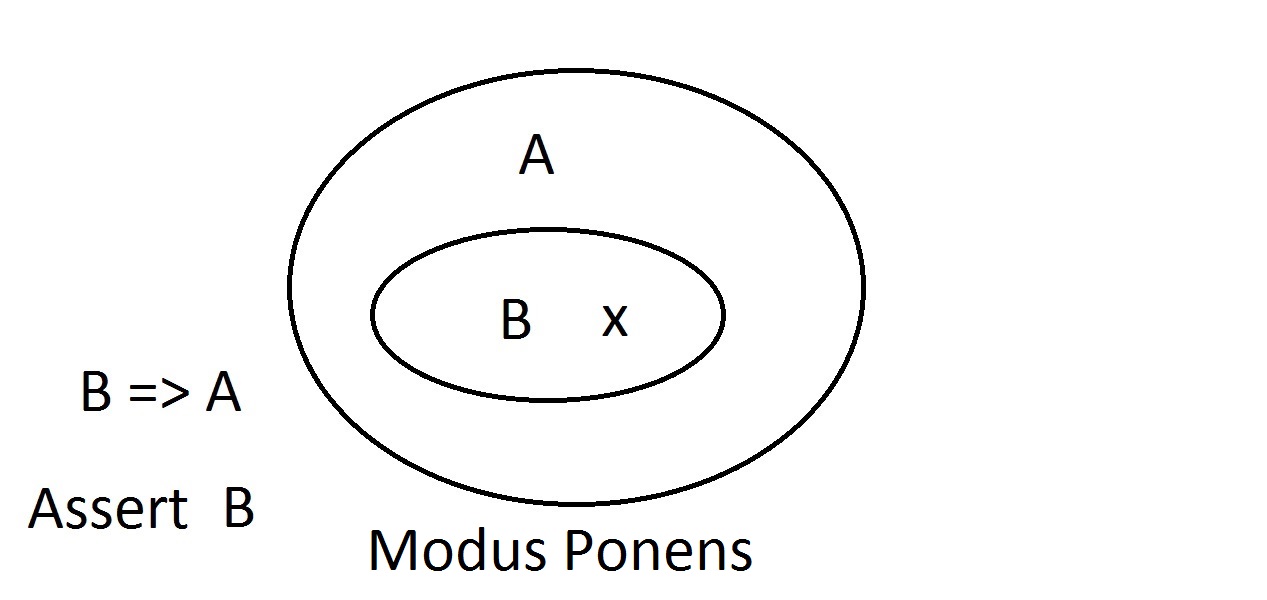Most azt állítjuk, hogy van valamink, aminek B tulajdonsága van. Bátran állíthatjuk, hogy ithoz A tulajdonság is tartozik. Ez a Modus Ponens (az előzményt megerősítő) érvelés. Bármely B tulajdonságú entitásnak nyilvánvalóan az A tulajdonságú térben is lennie kell.
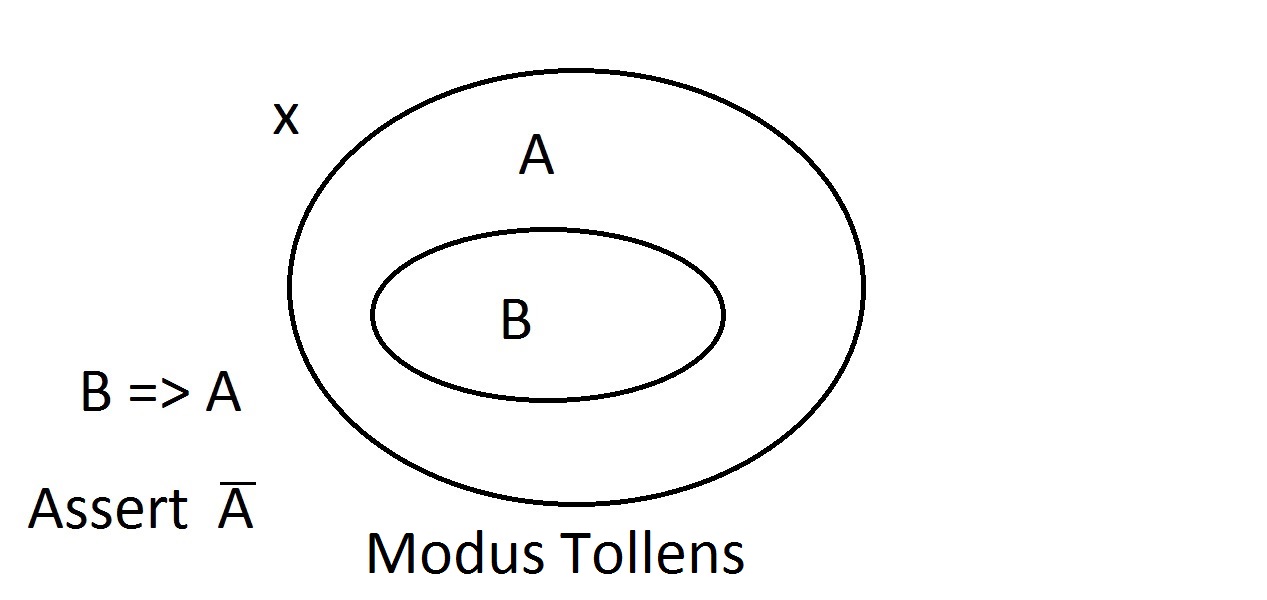Tegyük fel, hogy most azt állítjuk, hogy egy entitásnak nincs A tulajdonsága. A Venn-diagramból látható, hogy nem lehet B tulajdonsága sem. Bármi, ami az A tulajdonságú téren kívül van, annak a B tulajdonságú téren kívül is kell lennie. Ez a Modus Tollens (a következmény tagadása) érvelés, érvényes és erős.
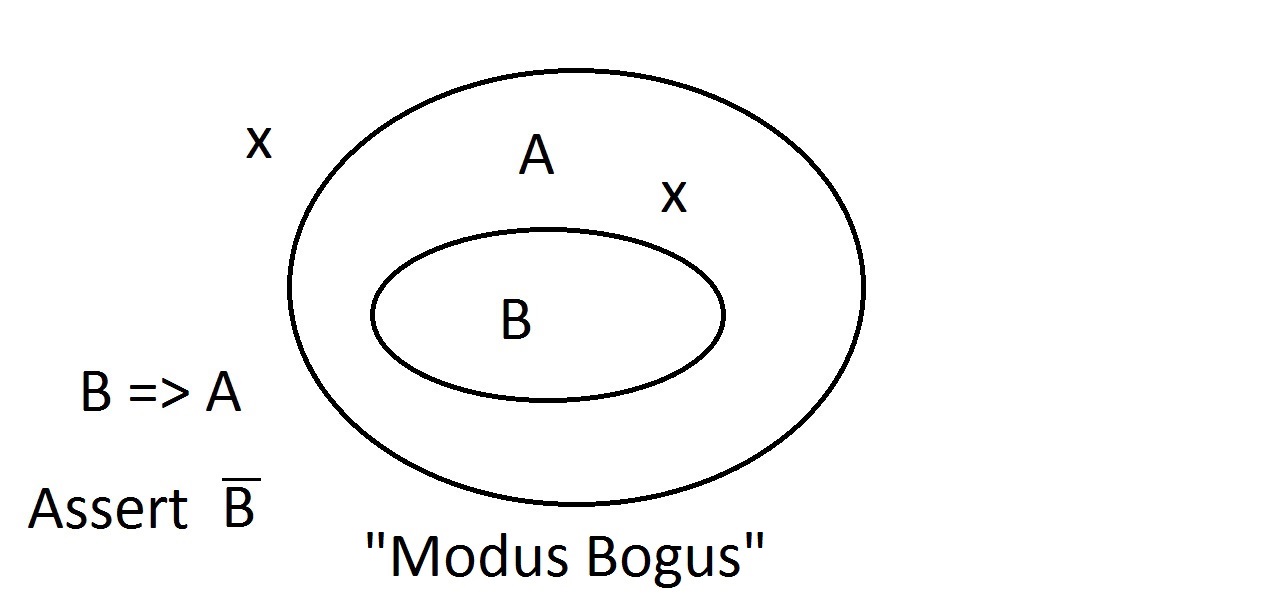Most megpróbáljuk azt állítani, hogy a dolog nem rendelkezik a B tulajdonsággal. Egy pillantás aVenn-diagramra megmutatja az itteni problémát. A B tulajdonsággal nem rendelkező entitás feküdhet az A téren belülvagy azon kívül. A “nem B” állítás semmit sem mond nekünk A-ról. Ez nem érvényesérvelés, ezért Modus Bogusnak neveztük el. Ez az előzmény tagadása, és nem érvényes.
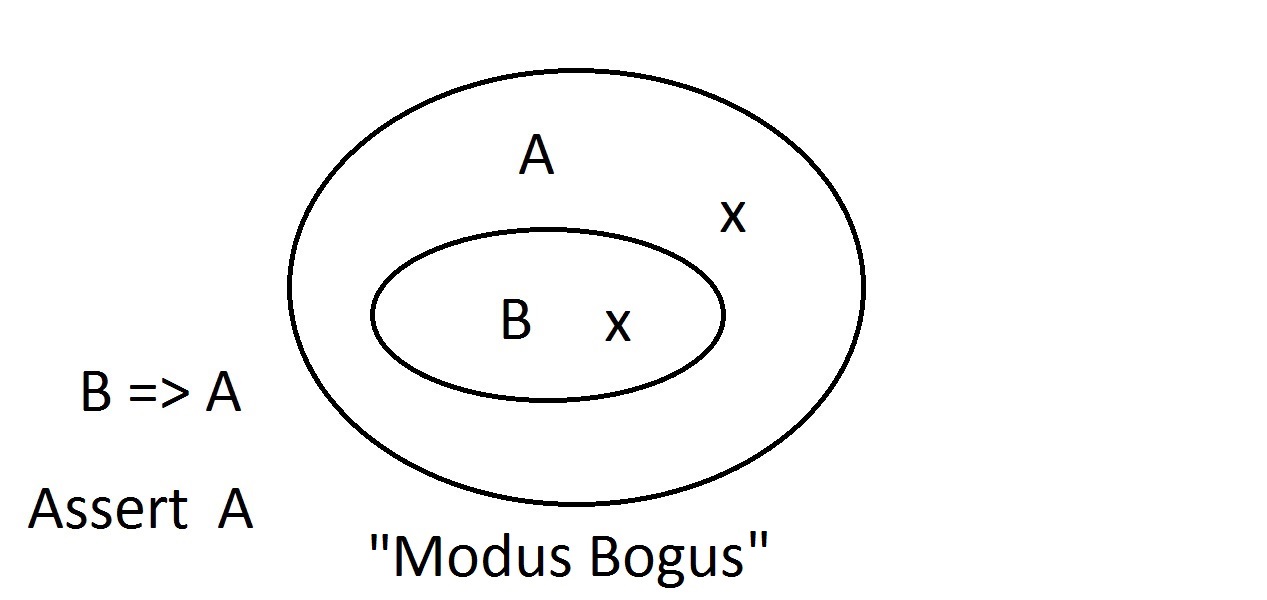Az utolsó lehetőség az, hogy azt állítjuk, hogy a dolognak A tulajdonsága van.A Venn-diagram mutatja a problémát. Az entitás bárhol feküdhet az A térben,a B téren belül vagy kívül. Azzal, hogy azt állítjuk, hogy a dolognak van Atulajdonsága, semmit sem mondunk arról, hogy B-vel is rendelkezik-e. Ez is Modus Bogus, vagyis érvénytelen érvelés.ezt hívják a következmény megerősítésének.
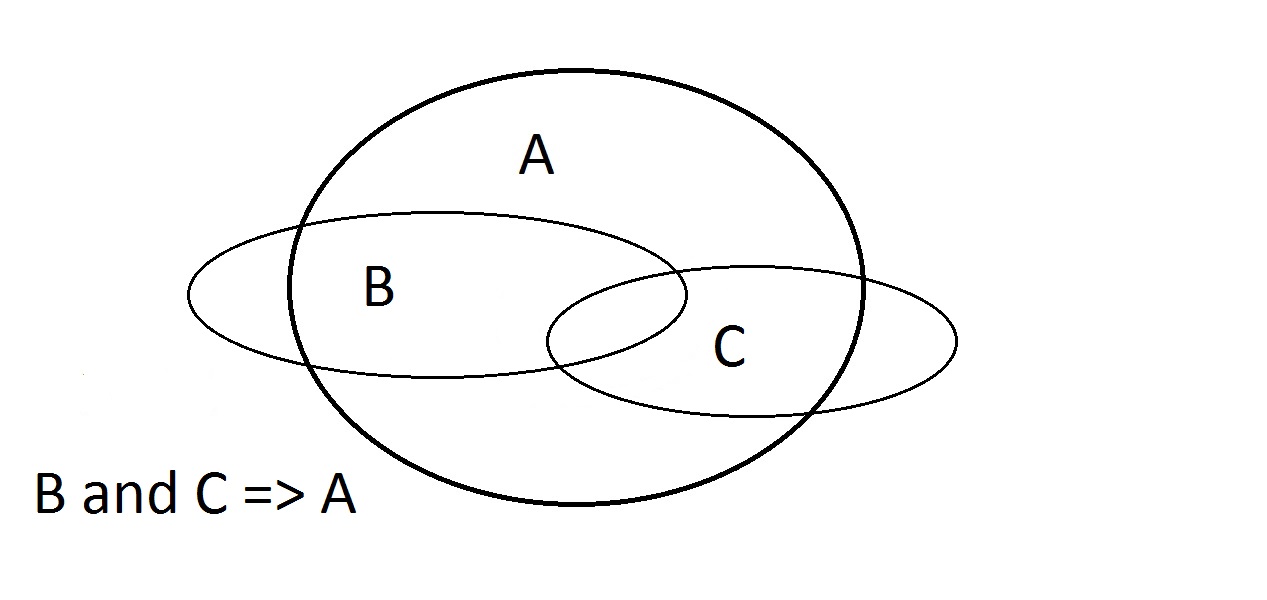Itt A, B és C tulajdonságokkal van dolgunk.itt csak azt tudjuk garantálni, hogy egy B-vel és C-vel rendelkező entitásnak A is van.vegyük észre, hogy a B és C terek egy része A-n kívül fekszik.

• Biztos A: Bárhol lehet A-ban
• Biztos B: B egy része A-n kívül fekszik
• Biztos C: C egy része A-n kívül fekszik
• Biztos A és B: Lehet, hogy magában foglalja C egy részét; lehet, hogy nem.
• B és C állítása: BC metszete teljes egészében A-ban fekszik. Azzal érvelve, hogy B és C => A működik.
• A és C állítása: Lehet, hogy B egy része benne van; lehet, hogy nem

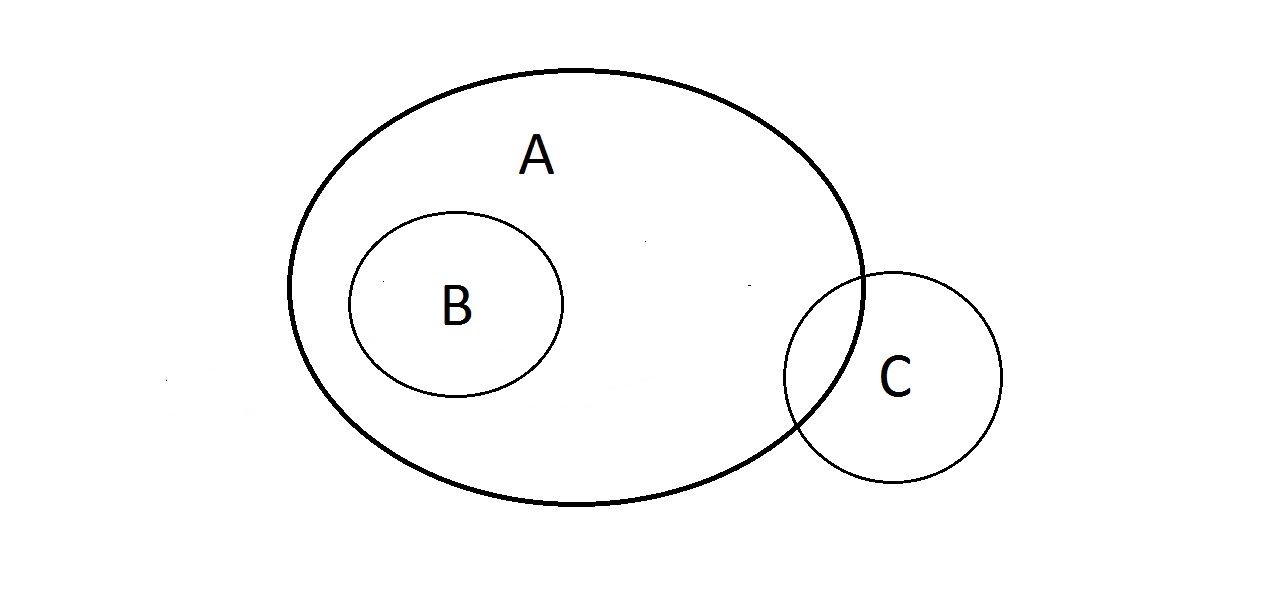
Mit lehet ezzel kezdeni? Az A és B tulajdonságok a fentiek szerint vannak, de mi a helyzet a C-vel? Valami, aminek C tulajdonsága van, lehet, hogy A-n belül van, de az is lehet, hogy nem. Valami, ami A-ban van, lehet, hogy C-ben is van, de lehet, hogy nem. Itt nem tudsz mit kezdeni C-vel. Arra viszont van garanciánk, hogy valaminek, aminek B van, A is van.

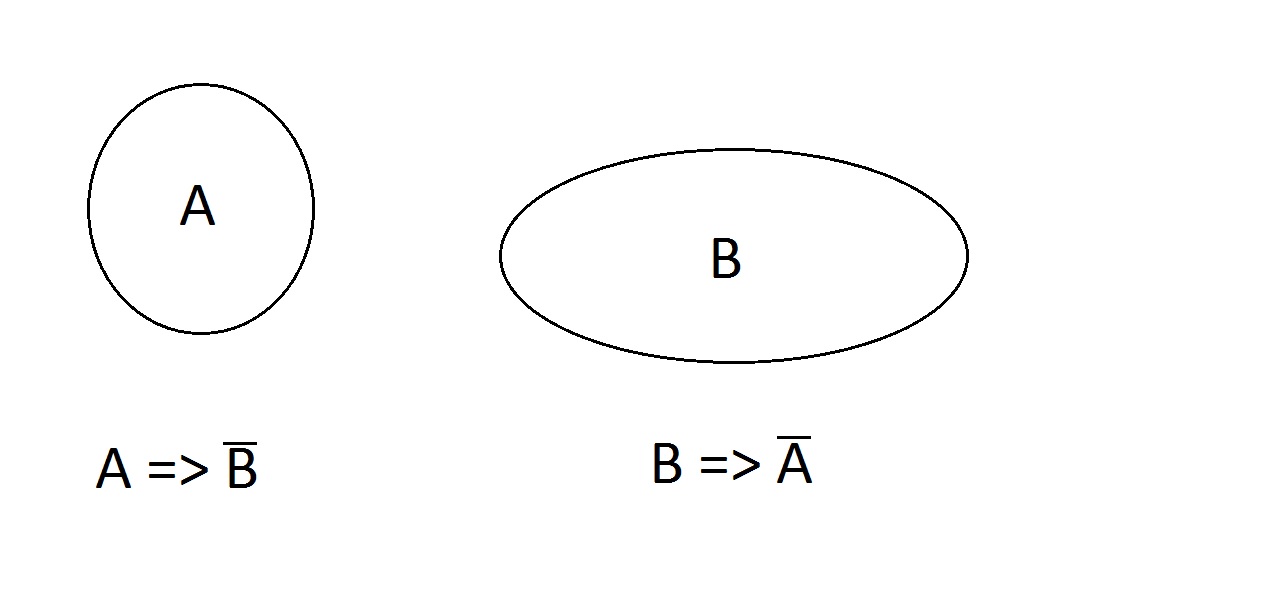
Hogyan állunk ezzel. A tulajdonságok kizárólagosak, egy entitás nem rendelkezhet egyszerre mindkettővel. nem rendelkezhet egyik, A vagy B-vel sem, de AB-vel sem. Az A=> nem B és a B => nem A állítások érvényesek.
Végül azt akarjuk, hogy az érvelésünk megalapozott legyen. Ehhez az érvelésnek a fentieknek megfelelően deduktívan érvényesnek kell lennie, és a premisszáknak a valóságban igaznak kell lenniük. Ez azt jelenti, hogy minden hangzatos érv érvényes, de nem feltétlenül minden érvényes érv hangzatos.

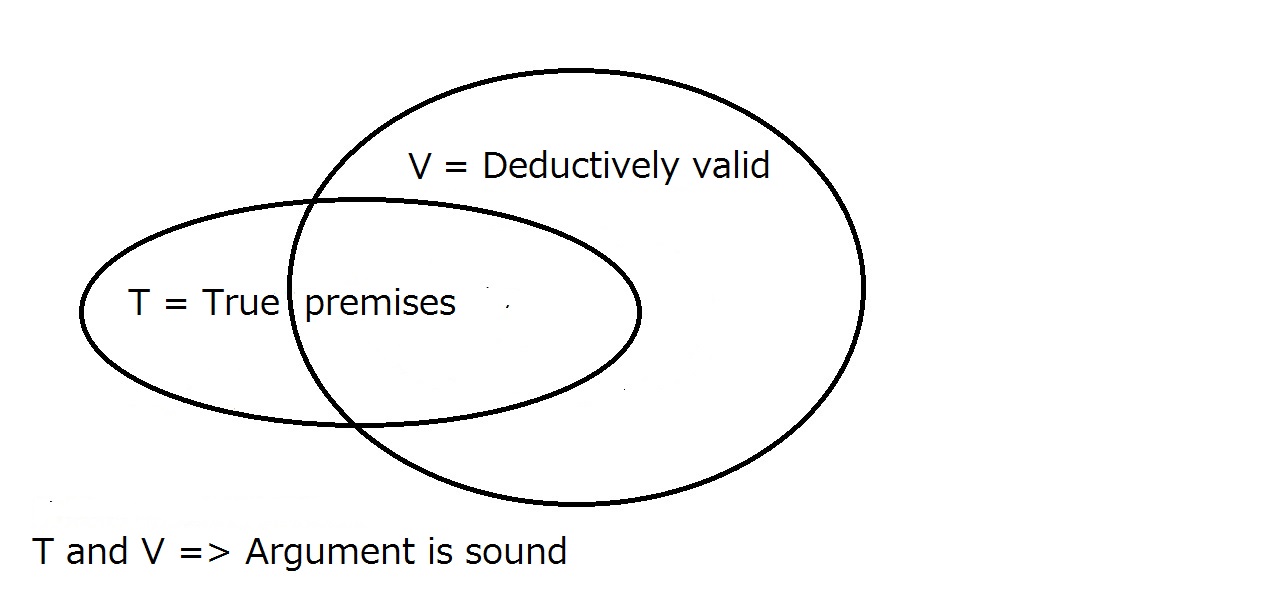
Egy hangzatos érv megköveteli, hogy deduktívan érvényes legyen és igaz premisszákkal rendelkezzen.Az egyik megléte nem garantálja automatikusan a másikat. Az a régió, amely mind a T-n, mind a V-n belül van, a hangzó érvek régiója.

Így látom én ezt. Mindenki figyeljen rám.

Aristotelész (Kr. e. 384-322)

Az http://www.rwe.org/images/aristotle.jpgExperiment-ből?
Self-consistent?
Ha az elméleted nem önkonzisztens, vagy az elméleted nem felel meg a gondos kísérleteknek, akkor az elméleted téves. Nem számít, hogy az elmélet mennyire szép; téves.

Galileo Galilei (1564-1642)

Forrás http://helios.gsfc.nasa.gov/galileo.jpg

pl. Euklidész ötödik posztulátuma.

(1) Bármely két különböző ponton keresztül lehet egy egyenest húzni.
(2) Egy véges egyenes folytonosan egyenesen meghosszabbítható.
(3) Egy kör leírható úgy, hogy bármely pont a középpontja és bármely távolság a sugara.
(4) Minden derékszög egyenlő.
(5) Egy adott ponton keresztül csak egy egyenest lehet párhuzamosan húzni.
A “pont” és az “egyenes” szavaknak nincs belső jelentése.
A “pont” és az “egyenes” szavakat felcserélhetnénk, és akkor is igaz lenne a tétel.
Mondhatnánk
(1) Bármely két különböző szögön keresztül lehet egy fleem…
Az ötödik posztulátumot kétféleképpen lehet megváltoztatni:
(5) Egy adott ponton keresztül nem lehet egy adott egyenessel párhuzamos egyenest húzni.
(5) Egy adott ponton keresztül sok egyenes lehet egy adott egyenessel párhuzamos.
Mindkét új posztulátum különböző KONZISZTENS geometriákat eredményez.melyik a helyes? Mindegyiknek igaza van! Melyik írja le ezt az Univerzumot?Ez a Fizika!