Notatki profesora Fishera na ten temat w PDF
Slajdy profesora Fishera na ten temat w PDF (wymagane hasło)
Stare slajdy profesora Sekuli w PDF.

Indukcja

Uwaga: Filozofowie (w tym prof. Fisher) odróżniają indukcję (uogólnianie cech jakiejś próbki na inne rzeczy) od abdukcji (wnioskowanie o najlepszym wyjaśnieniu), podczas gdy poniższa treść rozmywa oba te pojęcia pod jednym hasłem „indukcja”. Kiedy bierzesz tę klasę z profesorem Fisherem, lepiej polegać na jego notatkach lub slajdach na ten temat, niż na treści poniżej.

Indukcja jest procesem próbującym rozgryźć działanie jakiegoś zjawiska poprzez studiowanie jego próbki. Pracujesz z próbką, ponieważ przyjrzenie się każdemu składnikowi zjawiska nie jest wykonalne.Indukcja jest procesem twórczym. Naukowiec musi dokładnie zbadać próbkę zjawiska, a następnie sformułować hipotezę wyjaśniającą to zjawisko.Następnie następuje proces naukowy polegający na testowaniu hipotezy.Naukowcy, którzy uzyskują najbardziej spektakularne wyniki badań, to ci, którzy są wystarczająco kreatywni, aby wymyślić właściwe pytania badawcze.

Nauki przyrodnicze (fizyka, chemia, biologia itp.) są indukcyjne.Zbierane są dowody. Metoda naukowa jest stosowana.Zacznij od konkretnych wyników (próbka) i spróbuj odgadnąć ogólne zasady. Hipotezy mogą być tylko obalone, nigdy udowodnione. Jeśli hipoteza wytrzymuje wielokrotne próby przeprowadzane przez wielu niezależnych badaczy, rośnie zaufanie do niej. All hypotheses are tentative; any one could beoverted tomorrow, but very strong evidence is required to overthrowa „Law” or „Fact”.

Specific -> General

Here’s an example of induction: Załóżmy, że z dużego worka z kuleczkami wziąłem losowo 20 kulek. Okazało się, że każda z nich jest biała. To jest moje spostrzeżenie – każdy kamyk, który wyjąłem, był biały. Mógłbym zatem sformułować hipotezę, że można by to wyjaśnić, gdyby wszystkie kulki w worku były białe. Może się okazać, że w woreczku znajdują się różnokolorowe kulki, a moja pierwsza próbka po prostu ich nie trafiła.

Nawiasem mówiąc, jest to jeden z przypadków, w których możemy udowodnić prawdziwość hipotezy.Możemy po prostu wyrzucić wszystkie kulki z woreczka i zbadać każdą z nich.Taka procedura nazywa się spisem ludności – należy przyjrzeć się każdej z nich. W większości przypadków, w których stosuje się indukcję, spis nie jest wykonalny.

Abdukcja: Inference to Best Explanation

Jest to metoda rozumowania, która nie jest rygorystyczna jak Dedukcja.Załóżmy, że masz obserwacje interesującego zdarzenia. Nie jesteś natychmiast pewien, co wyjaśnia te obserwacje. Myślisz o wszystkich możliwych hipotezach, które mogłyby wiarygodnie wyjaśnić obserwacje. Jest to proces twórczy, w przeciwieństwie do dedukcji. Musisz wiedzieć jak najwięcej o sytuacji, aby ten proces był skuteczny. Biorąc pod uwagę wszystko, co wiesz, wybierasz hipotezę, która wydaje się najbardziej rozsądna i prawdopodobna. Wybrałeś pozornie najlepsze wyjaśnienie, choć może się ono mylić. Nie ma żadnej gwarancji. Dalsze sprawdzanie twojego wyjaśnienia jest zazwyczaj dobrym pomysłem, jeśli jest to możliwe; możesz znaleźć więcej informacji, które mogłyby sprawić, że ponownie rozważysz swój wniosek.

Ten rodzaj rozumowania jest mocną stroną Sherlocka Holmesa. Conan Doyle’s sfamously hiper-observant detektyw zauważa nawet bardzo małe wskazówki, że inspektor policji zwykle przegapić. Holmes łączy te wskazówki z ogólną wiedzą, jaką zgromadził na temat sprawy, aby wymyślić najlepsze wyjaśnienie – whodunit! On również wyjaśnia, jak zbrodnia została wykonana.W miłym akcentem dla czytelnika, Holmes często wyjaśnia rozumowanie, które doprowadziło go do rozwiązania. To wydaje się proste, kiedy Holmes wyjaśnia to …

Dedukcja

Matematyka jest nauką dedukcyjną. Aksjomaty są proponowane. Nie są one testowane; zakłada się, że są prawdziwe. Twierdzenia są wydedukowane z aksjomatów. Given the axioms and the rules of logic, a machine couldproduce theorems.

General -> Specific

Start with the general rule and deduce specific results.If the set of axioms produces a theorem and itsnegation, the set of axioms is called INCONSISTENT.

Suppose we have the following known conditions.

• Mamy duży worek kulek.
• Wiemy, że wszystkie kuleczki w worku są białe.
• Mam losową próbkę 20 kulek pobranych z worka.

Z nich mogę wywnioskować, że wszystkie kuleczki w próbce są białe, nawet bez patrzenia na nie. Ten rodzaj rozumowania nazywamy modus ponens (więcej na ten temat poniżej i w notatkach prof. Fishera).

A co powiesz na to?

• Mamy duży worek kulek.
• Wszystkie kulki w worku są białe.
• Mam próbkę 20 kulek o mieszanych kolorach.

Z tego szybko wnioskuję, że próbka nie została pobrana z worka białych kulek. Ten rodzaj rozumowania nazywamy modus tollens (więcej na ten temat poniżej i w notatkach prof. Fishera).

Dedukcyjne argumentowanie

Przyjrzyjrzyjmy się idei dedukcyjnego rozumowania (zaczerpniętej z notatek prof. Fishera).Prof. Fisher zauważa, że filozofowie zazwyczaj przedstawiają to jako

1. Premise number 12. Premise number 2...------------------------C. Conclusion to be reached

Ta struktura stanowi argument.Czasami zapisuje się ją jako
Przesłanka 1, Przesłanka 2, Przesłanka… =>Wniosek.
Skróćmy to do sylogizmu w ten sposób:
P =>C (Przesłanki implikują Wniosek, tak jak powyżej)
To po prostu oznacza, że jeśli przesłanki są prawdziwe, to wniosek też jest prawdziwy.
„Aby argument był dobry, musi mieć prawdziwe przesłanki, a przesłanki muszą oferować wsparcie dla wniosku. Najsilniejsze możliwe wsparcie dostarczyłoby absolutnej gwarancji, że wniosek będzie prawdziwy (zakładając, oczywiście, że przesłanki są prawdziwe).Rozważymy ten rodzaj wsparcia najpierw, ale potem przejdziemy do rozważenia słabszych rodzajów wsparcia, jak również.” (od prof. Fishera)
Jednym ze szczególnie użytecznych rodzajów argumentów jest argument ważny dedukcyjnie. (Jest to często skracane jako „argument ważny” lub czasami jako „argument dedukcyjny”.)Argumenty dedukcyjnie ważne to argumenty, w których przesłanki, gdyby były prawdziwe, byłyby najsilniejszym możliwym dowodem na to, że wniosek jest prawdziwy. Rzeczywiście te argumenty zapewniają następującą gwarancję: jeśli przesłanki są prawdziwe, to wniosek również musi być prawdziwy.

An argument, który wydaje się być dedukcyjny, ale ma przesłanki, które nie wspierają wniosku (brak gwarancji) jest invalidargument.
Powtórzmy sylogizm P => C (przesłanki prowadzą do wniosku).Istnieją cztery możliwe twierdzenia, które można na ten temat sformułować:

1. Wszystkie przesłanki są prawdziwe (P jest prawdziwe) (rozumowanie modus ponens)
2. Jedna lub więcej z przesłanek jest fałszywa (P jest fałszywe -. nie P)
3. Wniosek jest prawdziwy (C jest prawdziwe)
4. Wniosek jest fałszywy (C jest fałszywe – nie C) (rozumowanie modus tollens)

Tylko dwie z nich (#1 i #4) stanowią rozumowanie dedukcyjnie poprawne.Przyjrzyjmy się powodom takiego stanu rzeczy, po jednym wyborze na raz.

1. P jest prawdziwe (P) – Potwierdzenie przesłanki. Jeśli wszystkie przesłanki są prawdziwe, to wniosek musi być prawdziwy. Jest to bardzo mocny argument. (modus ponens)
2. P jest fałszywe (nie P) – Zaprzeczenie antecedencji. P jest fałszywe nie gwarantuje, że C jest albo prawdziwe, albo fałszywe. There could be other causes.
3. C is true (C) – Potwierdzenie następstwa. Jeśli C jest prawdziwe to może być z jednego z kilku powodów, a nie z tego konkretnego P.
4. C jest fałszywe (nie C) – Zaprzeczenie następstwa. Tutaj, jeśli C jest fałszywe toP musi być również fałszywe. Gdyby P było prawdziwe, to C też by było. (modus tollens)

W skrócie, #1 i #4 (modus ponens i modus tollens) są dedukcyjnie poprawne, podczas gdy #2 i #3 nie są.
Jeśli przesłanki odnoszą się do rzeczy w prawdziwym świecie, nadal musisz zrobić test na nieważność. Istnieją co najmniej trzy podejścia.

1. Sprawdź, czy możesz znaleźć scenariusz, w którym przesłanki są prawdziwe, ale wniosek jest fałszywy.
2. Spróbuj zastąpić rzeczownik lub przymiotnik w argumencie innym.Zamień wszystkie przypadki. Jeśli to oczywiście nie jest ważne, to oryginał nie był ważny.
3. Przedstaw P i C w diagramie Venn.Jeśli można to zrobić tak, że P jest prawdziweebut C jest fałszywe, argument jest nieważny. Zrobiliśmy te diagramy dla Ciebie poniżej.

Teraz poruszamy temat diagramów Venna. Mogą one być bardzo pomocne w sprawdzaniu przesłanek argumentu.

Schematy Venna

Schematy Venna są graficzną metodą przedstawiania logiki.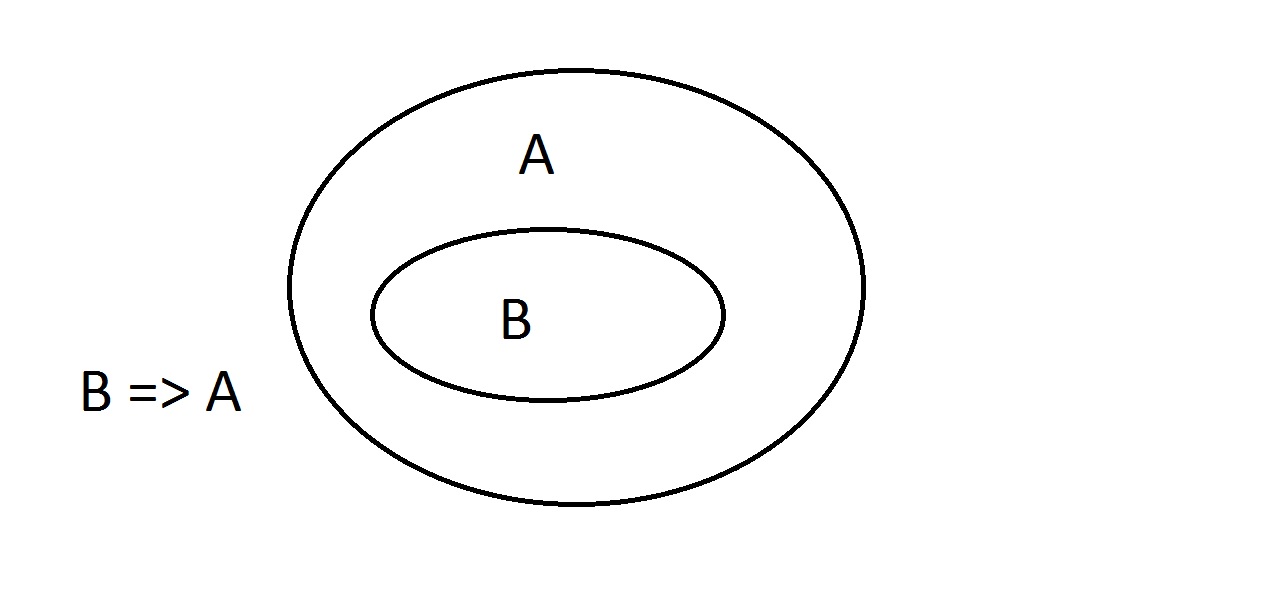
To jest najprostszy schemat, jaki można otrzymać. Zewnętrzny owal zawiera wszystkie rzeczy posiadające własność A, podczas gdy wewnętrzny owal zawiera wszystkie rzeczy posiadające własność B, jak również własność A.Jest to pokazane jako B=>A, co oznacza, że wszystkie rzeczy posiadające własność B mają również własność A.Można również powiedzieć „B implikuje A. „Jeśli B jest prawdziwe, to A musi być również. To jest gwarancja wspomniana powyżej.
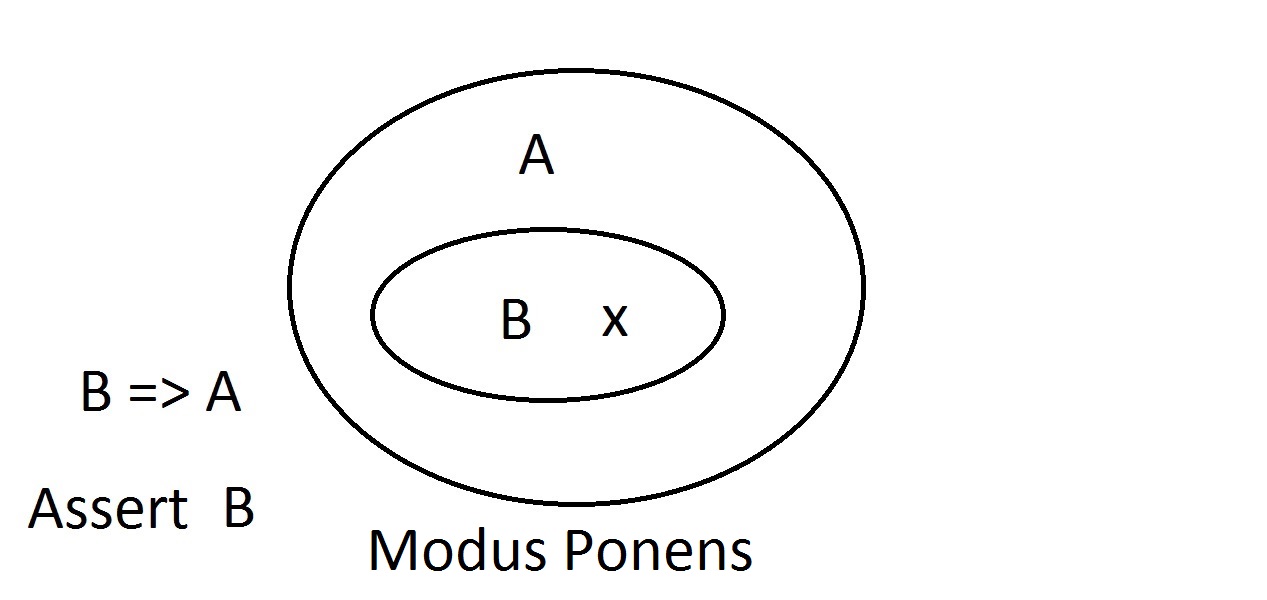Teraz będziemy twierdzić, że mamy coś z własnością B. Możemy śmiało argumentować, że ma ono również własność A. Jest to rozumowanie Modus Ponens (potwierdzające poprzednik). Każdy byt z własnością B oczywiście musi być również w przestrzeni własności A.
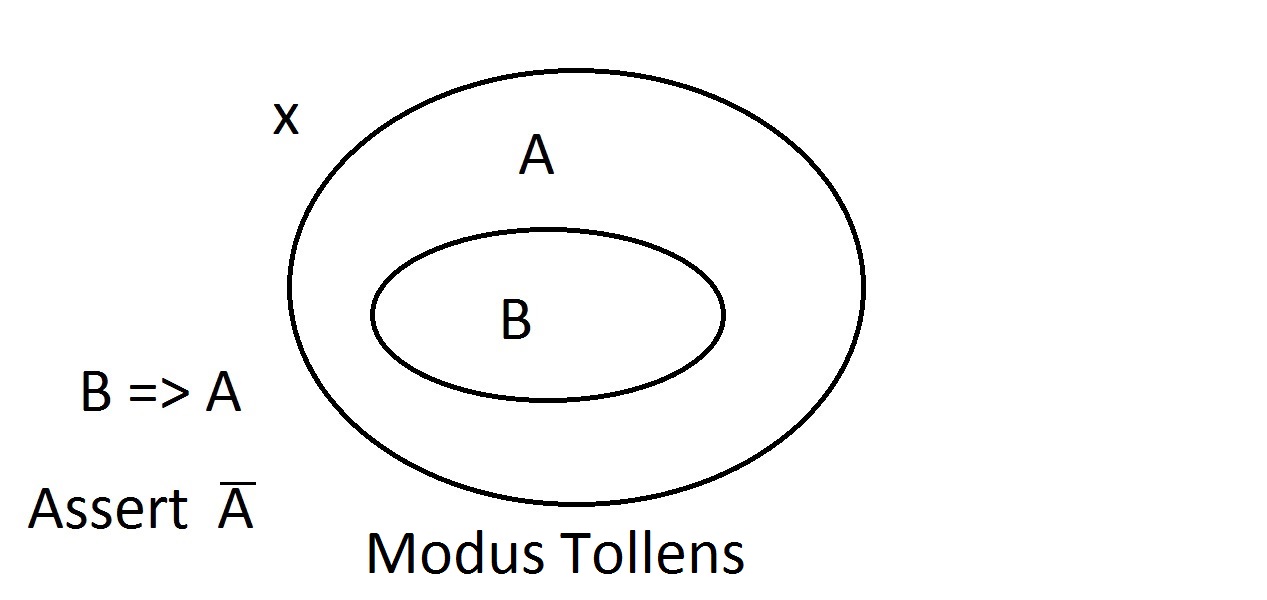Załóżmy, że teraz twierdzimy, że jakiś byt nie ma własności A. Diagram Venna pokazuje, że nie może mieć również własności B. Wszystko, co jest poza przestrzenią własności A, musi być również poza przestrzenią własności B. Jest to rozumowanie Modus Tollens (zaprzeczające skutkowi) i jest ono ważne i silne.
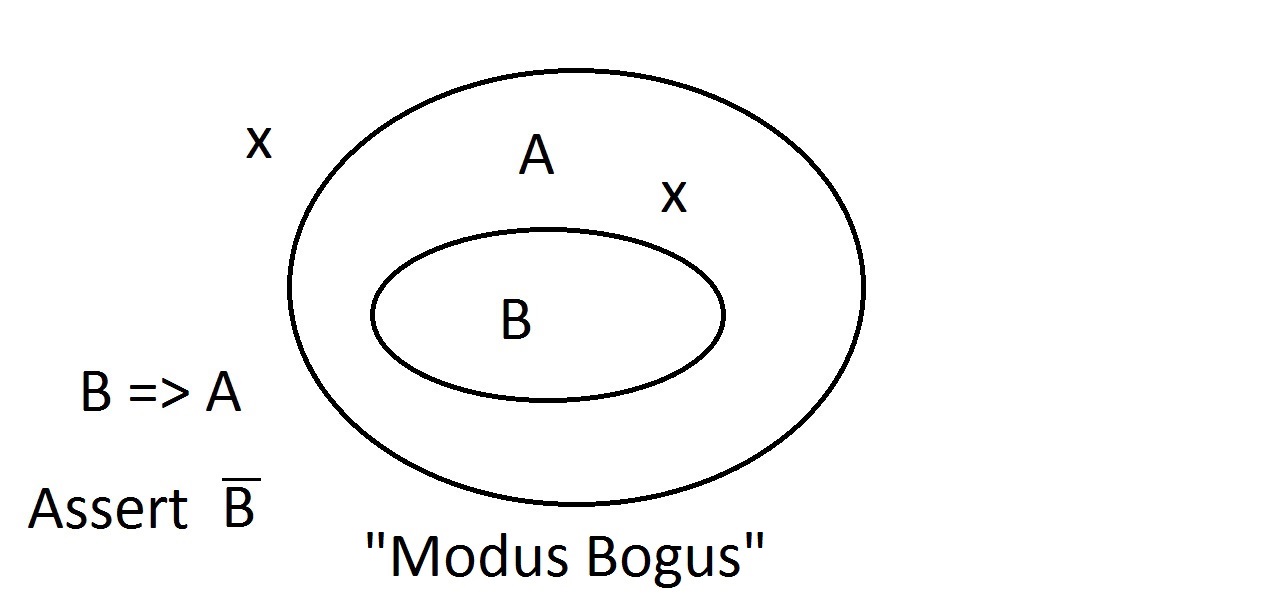Spróbujemy teraz twierdzić, że nasza rzecz nie posiada własności B. Spojrzenie na diagram Venna pokazuje, na czym polega problem. Byt nie posiadający własności B może leżeć wewnątrz przestrzeni A lub poza nią. Twierdzenie „nie B” nie mówi nam nic o A. To nie jest poprawne rozumowanie, więc nazwaliśmy je Modus Bogus. Jest to zaprzeczanie poprzednikowi i nie jest ważne.
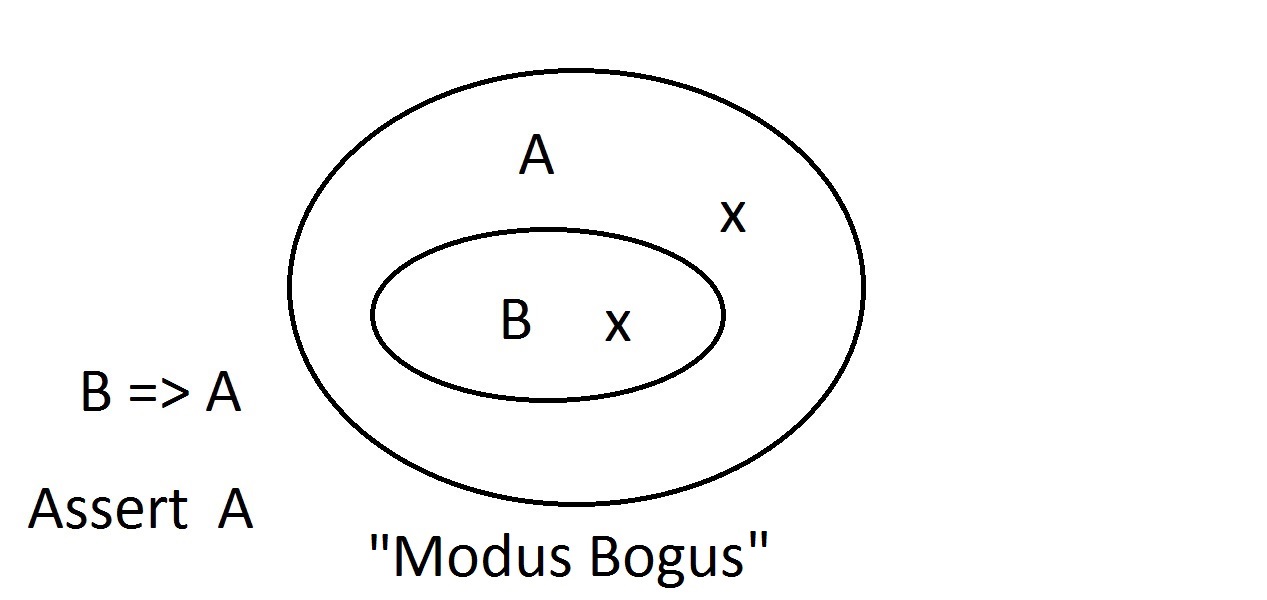Ostatnią możliwością jest twierdzenie, że nasza rzecz ma własność A.Diagram Venn pokazuje problem. Istota może leżeć gdziekolwiek w przestrzeni A, albo wewnątrz albo na zewnątrz przestrzeni B. Twierdzenie, że rzecz ma własność A nie mówi nic o tym, czy ma ona również B. Jest to również Modus Bogus, czyli błędne rozumowanie. Nazywa się to Afirmacją Konsekwencji.
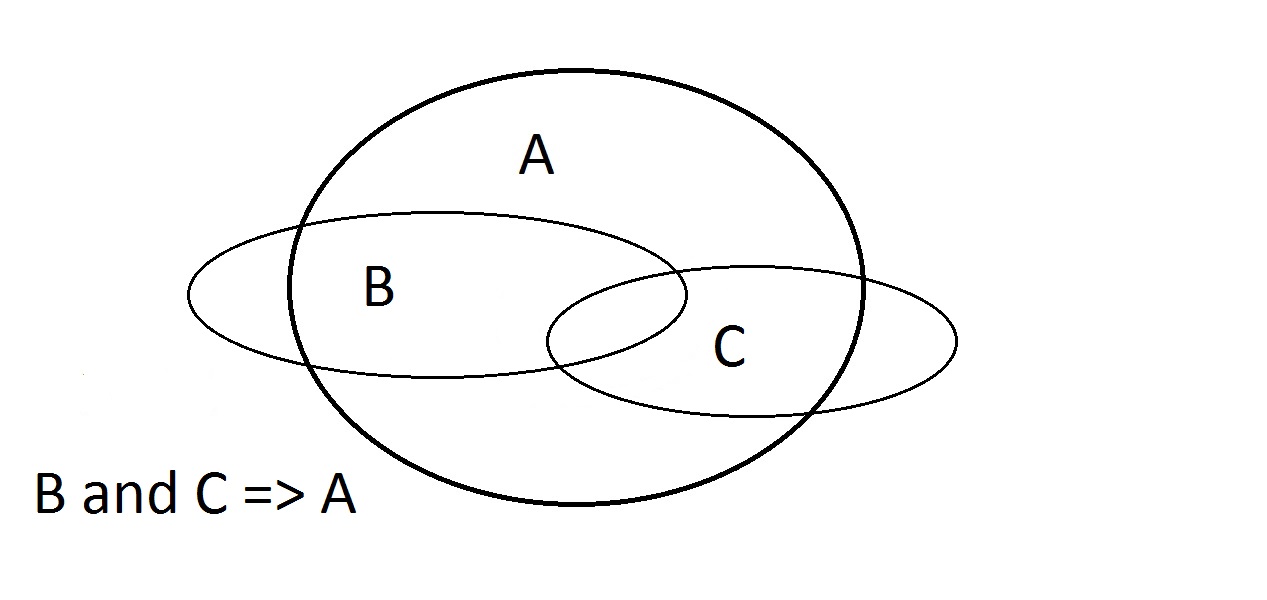Tutaj mamy do czynienia z własnościami A, B i C. Tutaj możemy zagwarantować tylko to, że istota posiadająca B i C posiada również A. Zauważmy, że niektóre przestrzenie B i C leżą poza A.

• Assert A: Could be anywhere in A
• Assert B: Some of B lies outside of A
• Assert C: Some of C lies outside of A
• Assert A and B: Might include some C; might not.
• Assert B and C: The intersection BC lies entirely in A. Arguing that B and C => A works.
• Assert A and C: Might include some B; might not

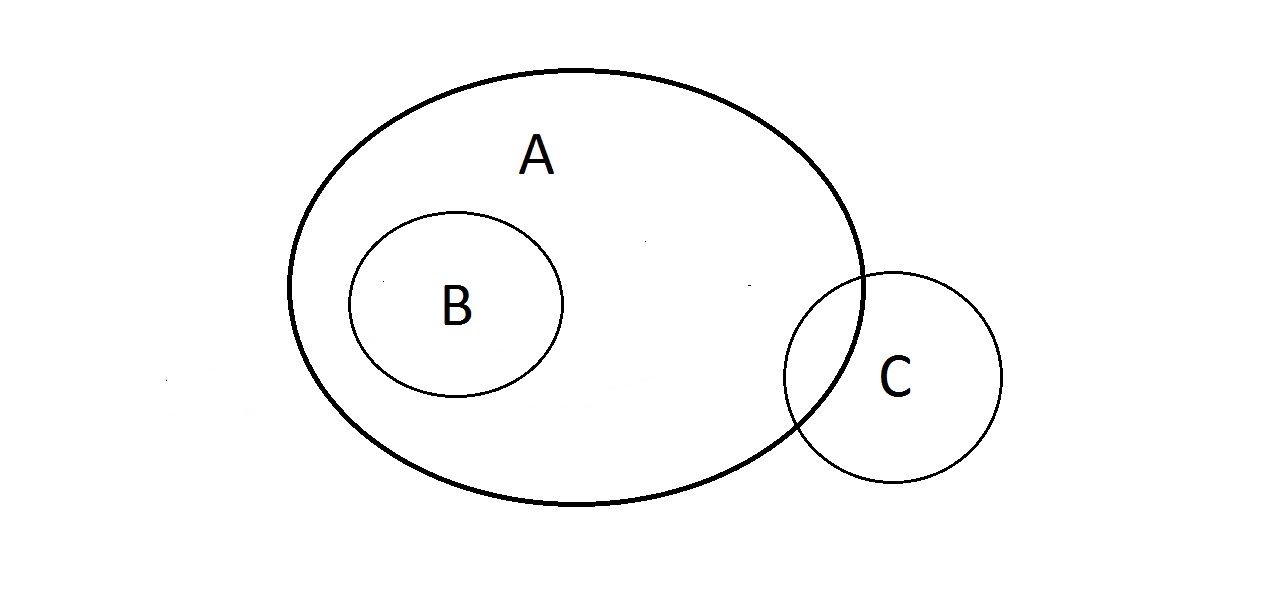
Co można z tym zrobić? Własności A i B są takie jak powyżej, ale co z C? Coś, co ma własność C może leżeć w A lub nie. Coś w A może być również w C lub nie. Z C nie da się tu nic zrobić. Mamy jednak gwarancję, że coś posiadającego B posiada również A.

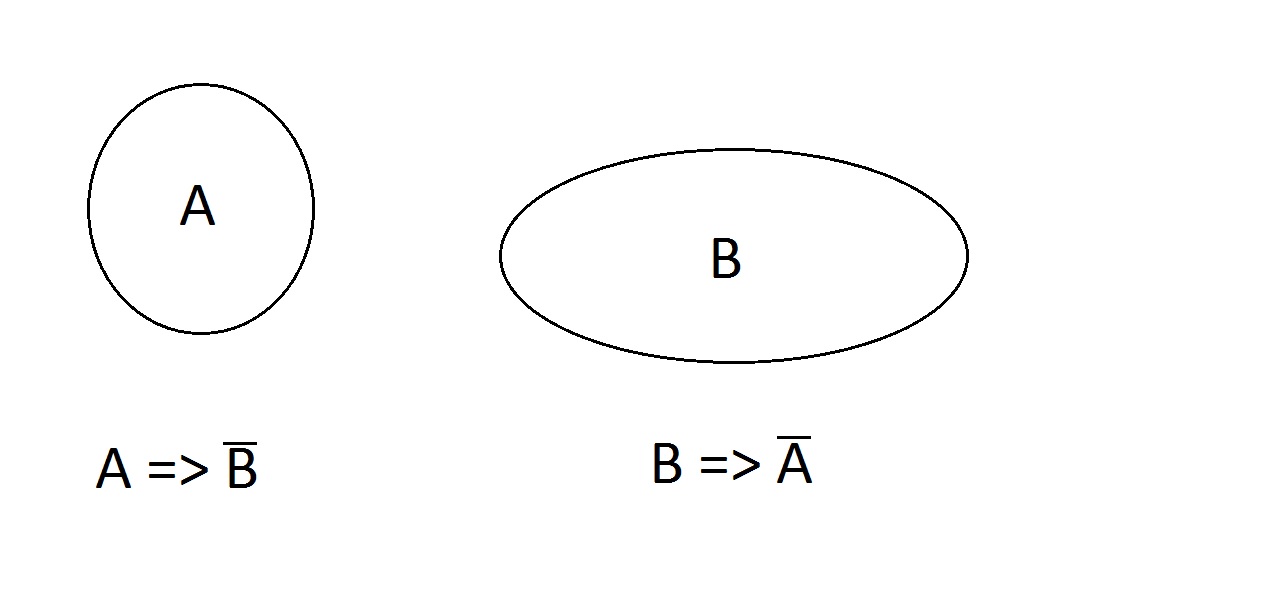
Co powiesz na to. Własności są wykluczające się; byt nie może mieć obu jednocześnie.Może nie mieć żadnej, A, lub B, ale nie AB. Stwierdzenia A=>nie B i B =>nie A są ważne.
Na koniec chcemy, aby nasz argument był solidny. Aby to się stało, argument musi bedeductively ważne jak powyżej i przesłanki muszą być prawdziwe w świecie rzeczywistym. Oznacza to, że wszystkie rozsądne argumenty są ważne, ale wszystkie ważne argumenty niekoniecznie są rozsądne.

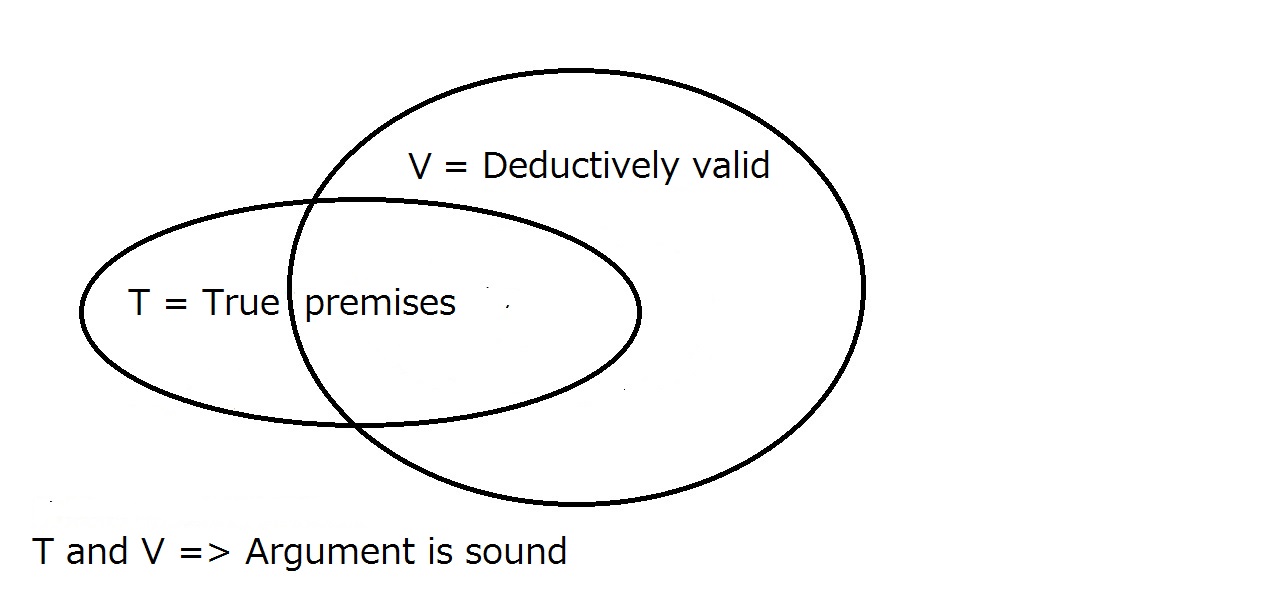
Dobry argument wymaga, aby był dedukcyjnie ważny i miał prawdziwe przesłanki.Posiadanie jednego nie gwarantuje automatycznie drugiego. Region, który znajduje się zarówno wewnątrz T jak i V jest regionem zdrowych argumentów.

Ja widzę to tak. Wszyscy mnie słuchajcie.

Arystoteles (384-322 p.n.e.)

Od http://www.rwe.org/images/aristotle.jpgExperiment?
Self-consistent?
Jeśli twoja teoria nie jest self-consistent, lub twoja teoria nie zgadza się z ostrożnymi eksperymentami, to twoja teoria jest błędna. Nie ma znaczenia, jak piękna jest teoria; jest błędna.

Galileo Galilei (1564-1642)

Z http://helios.gsfc.nasa.gov/galileo.jpg

np. piąty postulat Euklidesa.

(1) Przez dowolne dwa różne punkty można poprowadzić jedną prostą.
(2) Prostą skończoną można przedłużać w sposób ciągły w linii prostej.
(3) Okrąg można opisać mając dowolny punkt za środek i dowolną odległość za promień.
(4) Wszystkie kąty proste są równe.
(5) Przez dany punkt można poprowadzić tylko jedną prostą równoległą do danej prostej.
Słowa „punkt” i „prosta” nie mają żadnego wewnętrznego znaczenia.
Można zamienić miejscami słowa „punkt” i „prosta” i nadal mieć prawdziwe twierdzenia.
Można powiedzieć
(1) Przez dowolne dwie różne łopatki można narysować jedną p…
Piąty postulat można zmienić na dwa sposoby:
(5) Przez dany punkt nie można poprowadzić żadnej prostej równoległej do danej prostej.
(5) Przez dany punkt można poprowadzić wiele prostych równoległych do danej prostej.
Oba te nowe postulaty dają różne KONSEKWENTNE geometrie.Który z nich jest słuszny? Wszystkie są! Która z nich opisuje ten Wszechświat? To jest FIZYKA!