
Galileo este adesea considerat părintele științei moderne. El a fost cel care a reunit principiile experimentului, teoriei și matematicii într-un cadru standard. Probabil că, mai mult decât oricine altcineva, Galileo a fost persoana responsabilă pentru dezvoltarea științei moderne.
Se spune că Galileo a aruncat două bile de oțel cu mase diferite, dar din același material, de pe turnul înclinat din Pisa și că acestea au aterizat în același timp. Ceea ce este remarcabil la acest experiment este că el a inaugurat o nouă metodă de a face știință, în care se face un experiment pentru a testa o ipoteză. El a arătat că trebuie să facem mai mult decât să credem că ceva este adevărat, ci trebuie să și demonstrăm acest lucru.

Galileu a descoperit un paradox interesant în timp ce era șeful Departamentului de Matematică de la Universitatea din Pisa.
Definiție: Un paradox, cunoscut și sub numele de antinomie, este o afirmație contradictorie din punct de vedere logic sau o afirmație care este contrară așteptărilor cuiva. (Wikipedia). (Greacă: „para” = dincolo, „doxa” = credință)
Paradoxul lui Galileo se referea la a determina dacă două seturi care conțin obiecte infinite sunt echivalente unul cu celălalt. De exemplu, fie P este ansamblul numerelor întregi pozitive unde P= {0,1,2,2,3,…} și E este ansamblul numerelor pare unde E = {0,2,4,6,…}. Galileo susținea că dimensiunile acestor două seturi vor fi aceleași pentru că putem împerechea fiecare număr întreg pozitiv din setul P cu numerele pare din setul E.

Atunci cum poate fi aceeași dimensiunea celor două seturi atunci când în E apare un număr „mai mic”? Acest lucru a fost numit paradoxul lui Galileo și a început o nouă dezbatere despre conceptul de infinit.
După Galileo, studentul său Evangelista Torricelli a devenit șeful Departamentului de Matematică de la Universitatea din Pisa. Este posibil să fi auzit de el datorită lucrărilor sale privind presiunea atmosferică și inventarea barometrului. Deoarece Toricelli este interesat și de matematică, el se întreabă:
Este posibil să avem un obiect cu un volum finit și o suprafață infinită? În primul rând, un astfel de lucru pare improbabil pentru cei mai mulți dintre noi. Cu toate acestea, matematica ne spune că un astfel de lucru s-ar putea întâmpla. Torricelli și-a răspuns singur la întrebare și a descoperit Trompeta lui Toricelli, a cărei suprafață este infinită, dar al cărei volum este finit. Descoperirea sa văzută ca un paradox „incredibil”.
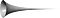
De altfel, există o regulă esențială în filozofia matematicii; Indiferent de epoca filozofiei sau a matematicii de care te ocupi, aceasta este legată de istoria, cultura și religia regiunii respective. De aceea se numește trompeta lui Toricelli și Cornul lui Gabriel. Aici se face o trimitere la Biblie, deoarece creștinii cred că îngerul Gabriel va sufla în corn în Ziua Judecății.
Atunci cum se formează trompeta lui Toricelli? Știm cu toții cum se face graficul y=x. Dacă, în schimb, reprezentați grafic ecuația y=1/x unde x este mai mare sau egal cu 1, graficul va fi așa:
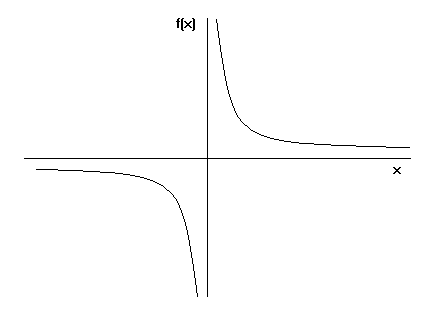
Când luăm graficul lui y=1/x și îl rotim în jurul axei x, vedem trompeta lui Toricelli.

Din fericire, avem în mână formule matematice pentru a calcula aria și volumul trompetei lui Toricelli. Când folosim formula de integrare de mai jos pentru volumul trompetei, obținem o cantitate finită.
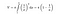
Dar, când aplicăm formula de integrare pentru suprafața trompetei, de data aceasta, suprafața acesteia devine infinită. Nu este interesant acest rezultat?
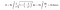
Din moment ce volumul trompetei lui Toricelli este finit, o putem umple cu o cantitate finită de vopsea. De exemplu, să presupunem că volumul acesteia este de 100 de litri. Mă duc la Home Depot și cumpăr 100 de litri de vopsea și o umplu. Cu toate acestea, ceea ce face acest lucru interesant este faptul că voi fi vopsit suprafața infinită cu acei 100 de litri de vopsea. Astăzi, cei mai mulți oameni numesc acest paradox, „paradoxul pictorului.”
Houston, avem o problemă aici! Situația care este imposibilă în practică devine posibilă în matematică. Așadar, cum poate fi reală trompeta lui Torricelli? Sau, cum putem potrivi cu exactitate toate elementele seturilor în timp ce unul dintre seturi este un subansamblu al altuia în exemplul lui Galileo?
Motivul pentru toate aceste conflicte este faptul că conceptul de infinit nu este similar cu alte concepte pe care le cunoaștem, iar acest lucru îi derutează pe mulți oameni. Galileo spune pentru paradoxul său,
„Da, prietene, există infinitul. Este zadarnic să te opui la el. Seturile la care lucrez eu sunt exemple de seturi închise care implică infinitul. Ele pornesc de la un punct și merg până la infinit, și totuși, sunt tot seturi. Cu toate acestea, comentariile și conceptele mele despre infinit trebuie să fie diferite de cele pe care le-aș folosi pentru mărimi finite. Dacă aveți de-a face cu mărimi finite, puteți spune că 3 kilograme sunt mai mici decât 5 kilograme, sau că 32 de metri sunt mai lungi decât 7 metri. Dar când vine vorba de infinit, nu poți spune că acest infinit este mai mare, mai mic sau egal cu acela.”
Aceasta a fost soluția lui Galileo în anii 1600.
Din păcate, soluția lui Galileo a declanșat o nouă dezbatere despre infinit. Matematicienii și filozofii nu au reușit să se pună de acord asupra unui răspuns specific până când Cantor a împărtășit „teoria seturilor”, pe care elevii o învață astăzi în școala primară.
Potem să istorisim periodic dezvoltarea ideii de infinit. Ea a apărut pentru prima dată de la Eleatici, care a fost o școală de filosofie presocratică fondată de Parmenide la începutul secolului al V-lea î.Hr. în orașul antic Elea. În această școală au existat trei mari filosofi, precum Zenon, Xenofan și Parmenide. În această școală, filozofia acceptată era că existența era singulară și că nu exista pluralitate. Zeno a fost faimos pentru paradoxurile sale despre infinit la Eleatici. Mai târziu, în anii 300 î.Hr, Aristoteles a apărut și a propus o pereche de concepte pentru a explica paradoxurile lui Zenon, care erau infinitul potențial și infinitul real.
Infinitul potențial este un grup de numere sau un grup de „lucruri” care continuă fără să se termine, continuând sau repetându-se la nesfârșit, fără un punct final recognoscibil.
Infinitul real implică seturi sau „lucruri” care nu se termină niciodată într-un spațiu care are un început și un sfârșit; este o serie care, din punct de vedere tehnic, este „terminată”, dar care constă dintr-un număr infinit de membri.
Aristotel credea că nu există un infinit real. Această idee a lui Aristotel a dominat lumea filozofiei până în anii 1600. Apoi, filozofi precum Cusa și Bruno au susținut că există un infinit real, dar nu putem să-i dăm un sens. După Cuso și Bruno, marele gânditor Spinoza s-a alăturat în acest subiect.
Spinoza a spus că putem înțelege conceptul de infinit și le-a clasificat în funcție de mărime. Cu toate acestea, el a declarat, de asemenea, că nu a putut face calcule matematice cu ele. De exemplu, el putea adăuga 3 la 5, dar nu putea adăuga un infinit la altul.
În cele din urmă, pentru a încheia aceste dezbateri, a apărut un om frumos, Georg Cantor, care a găsit teoria seturilor, care este încă baza matematicii. El a pus punctul final în discuțiile despre infinit cu teoria sa despre seturi.
Ne-a arătat că un set infinit ar fi mai mare sau mai mic decât un alt set infinit. Mai mult, Cantor a afirmat că putem adăuga și multiplica seturile de infinit. Până în acel moment, oamenii au urmat ideile lui Aristotel despre infinit. Potrivit lui Aristotel, dacă înmulțim numărul 3 cu infinitul, acesta ar fi din nou infinit. Infinitul ar înghiți totul. Pe baza acestui fapt, el susținea că ar exista doar un infinit potențial, nu un infinit real.
Cu toate acestea, Cantor ne-a demonstrat contrariul ideii lui Aristotel cu ajutorul teoriei seturilor. Dacă adăugăm unu la un set infinit, acesta nu va mai fi același set. El a încercat să compare infinitele. De exemplu, Cantor a demonstrat că ansamblul tuturor funcțiilor din (0,1)→ℕ este numărabil. Astfel, el a definit o funcție unu-la-unu și onto de la intervalul (0,1) la numerele naturale.
Cu alte cuvinte, el a demonstrat că toate numerele naturale pot încăpea între 0 și 1, deoarece între 0 și 1 existau infinite numere raționale, iar aceste infinituri pot fi împerecheate. Apoi a făcut ceva și mai periculos decât să găsească două infinituri egale. A comparat infinitatea numerelor reale cu infinitatea numerelor naturale și a constatat că infinitatea numerelor reale este mai mare decât cealaltă. El chiar s-a uitat la demonstrația sa și i-a spus prietenului său Dedekind: „O văd, dar nici eu nu pot să cred…”.
Cantor a fost, de asemenea, un matematician cu preocupări filosofice și religioase foarte serioase. În timp ce dezvolta teoria seturilor, el a spus: „Dumnezeu mi-a dictat teoria seturilor”.
Teoria seturilor nu a fost larg acceptată atunci când a fost dezvoltată pentru prima dată. Companiile nici măcar nu l-au angajat pe Cantor pentru vreo slujbă. Un matematician, Henri Poincaré, a spus odată: „Ideile acestui Cantor sunt o boală rea care se lipește de gulerul matematicii. Iar matematica îl va trata într-o bună zi”. Cantor a fost nevoit să meargă la un spital de nebuni pentru o vreme și a murit acolo. Dar astăzi, îl considerăm un geniu.
Cantor a fost un om singuratic la marginea infinitului. El a citat Biblia la începutul articolului său despre Numerele Transfinite: „Tot ceea ce este ascuns va fi scos la lumină.”
.