Identitatea lui Euler pare deconcertantă:

Ea apare dintr-o formulă mai generală:

Yowza – raportăm un exponent imaginar la sinus și cosinus! Și cumva dacă introducem pi rezultă -1? Ar putea fi acest lucru vreodată intuitiv?

Nu conform matematicianului Benjamin Peirce din anii 1800:

Este absolut paradoxal; nu-l putem înțelege și nu știm ce înseamnă, dar l-am demonstrat și, prin urmare, știm că trebuie să fie adevărul.

Argh, această atitudine îmi face sângele să fiarbă! Formulele nu sunt vrăji magice care trebuie memorate: trebuie, trebuie, trebuie să găsim o înțelegere. Iată-o pe a mea:

Formula lui Euler descrie două moduri echivalente de a te deplasa într-un cerc.

Asta e tot? Această ecuație uluitoare este despre rotirea în jurul valorii de? Da – și o putem înțelege bazându-ne pe câteva analogii:

• Începând de la numărul 1, vedeți înmulțirea ca pe o transformare care schimbă numărul: $1 \cdot e^{i \pi}$
• Creșterea exponențială regulată crește continuu 1 cu o anumită rată pentru o anumită perioadă de timp; creșterea exponențială imaginară îl rotește continuu pe 1 pentru o anumită perioadă de timp
• Creșterea pentru unități de timp „pi” înseamnă parcurgerea unei distanțe de pi radiani în jurul unui cerc
• În consecință, $e^{i \pi}$ înseamnă să începi de la 1 și să rotești pi (la jumătatea unui cerc) pentru a ajunge la -1

Aceasta este viziunea de nivel înalt, să ne scufundăm în detalii. Apropo, dacă cineva încearcă să vă impresioneze cu $e^{i \pi} = -1$, întrebați-l despre i la puterea i-a. Dacă nu se pot gândi până la capăt, formula lui Euler este încă o vrajă pentru ei.

Update: În timp ce scriam, m-am gândit că un videoclip ar putea ajuta la explicarea mai clară a ideilor:

Înțelegerea cos(x) + i * sin(x)

Semnul egal este supraîncărcat. Uneori vrem să spunem „să punem un lucru la altul” (cum ar fi x = 3), iar alteori vrem să spunem „aceste două lucruri descriu același concept” (cum ar fi $\sqrt{-1} = i$).

Formula lui Euler este cea din urmă: ea oferă două formule care explică cum să ne mișcăm într-un cerc. Dacă examinăm mișcarea circulară folosind trigonometria și ne deplasăm pe x radiani:

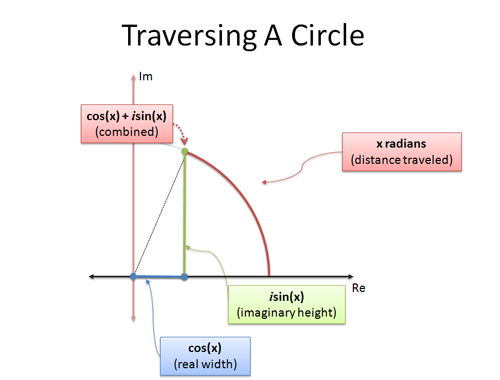
• cos(x) este coordonata x (distanța orizontală)
• sin(x) este coordonata y (distanța verticală)

Declarația

este o modalitate inteligentă de a îngloba coordonatele x și y într-un singur număr. Analogia „numerele complexe sunt bidimensionale” ne ajută să interpretăm un singur număr complex ca o poziție pe un cerc.

Când fixăm x la $\pi$, călătorim cu $\pi$ unități de-a lungul exteriorului cercului unitar. Deoarece circumferința totală este de $2\pi$, vechiul $\pi$ simplu este la jumătatea distanței, ceea ce ne plasează la -1.

Neato: Partea dreaptă a formulei lui Euler ($\cos(x) + i \sin(x)$) descrie mișcarea circulară cu numere imaginare. Acum haideți să ne dăm seama cum o realizează partea e a ecuației.

Ce este creșterea imaginară?

Combinarea coordonatelor x- și y- într-un număr complex este complicată, dar gestionabilă. Dar ce înseamnă un exponent imaginar?

Să facem un pas înapoi puțin. Când văd $3^4$, mă gândesc la el astfel:

• 3 este rezultatul final al creșterii instantanee (folosind e) cu o rată de ln(3). Cu alte cuvinte: $3 = e^{{\ln(3)}$
• $3^4$ este același lucru ca și cum ai crește până la 3, dar apoi crești de 4 ori mai mult. Deci $3^4 = e^{{\ln(3) \cdot 4} = 81$

În loc să vedeți numerele ca atare, vă puteți gândi la ele ca la ceva la care e a trebuit să „crească”. Numerele reale, cum ar fi 3, dau o rată a dobânzii de ln(3) = 1,1, și asta este ceea ce e „colectează” pe măsură ce se deplasează, crescând continuu.

Creșterea regulată este simplă: continuă să „împingă” un număr în aceeași direcție reală în care mergea. 3 × 3 împinge în direcția inițială, făcându-l de 3 ori mai mare (9).

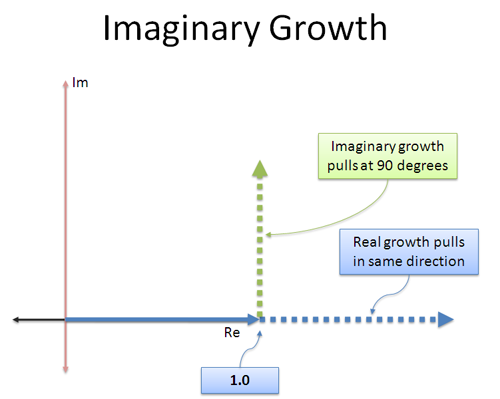
Creșterea imaginară este diferită: „dobânda” pe care o câștigăm este într-o direcție diferită! Este ca un motor cu reacție care a fost legat lateral – în loc să mergem înainte, începem să împingem la 90 de grade.

Ceea ce este interesant la o împingere ortogonală (perpendiculară) constantă este că nu te accelerează sau te încetinește – te rotește! Luând orice număr și înmulțind cu i nu-i va schimba magnitudinea, ci doar direcția pe care o indică.

Intuitiv, iată cum văd eu rata de creștere imaginară continuă: „Când cresc, nu mă împingeți înainte sau înapoi în direcția în care merg deja. În schimb, rotește-mă.”

Dar nu ar trebui să ne rotim din ce în ce mai repede?

Mi-am pus și eu această întrebare. Creșterea regulată se compune în direcția noastră inițială, așa că mergem 1, 2, 4, 8, 16, înmulțind de fiecare dată de 2 ori și rămânând în numerele reale. Putem considera acest lucru $e^{\ln(2)x}$, ceea ce înseamnă să creștem instantaneu cu o rată de ln(2) timp de „x” secunde.

Și hei — dacă rata noastră de creștere ar fi de două ori mai rapidă, 2ln(2) vs ln(2), ar arăta la fel ca și cum am crește de două ori mai mult timp (2x vs x). Magia lui e ne permite să schimbăm rata și timpul; 2 secunde la ln(2) este aceeași creștere ca și 1 secundă la 2ln(2).

Acum, imaginați-vă că avem o rată de creștere pur imaginară (Ri) care ne rotește până când ajungem la i, sau 90 de grade în sus. Ce se întâmplă dacă dublăm această rată la 2Ri, ne vom roti în afara cercului?

Nu! Având o rată de 2Ri înseamnă că pur și simplu ne rotim de două ori mai repede sau, alternativ, ne rotim cu o rată de R de două ori mai mult timp, dar rămânem pe cerc. Dacă ne rotim de două ori mai mult înseamnă că acum suntem orientați la 180 de grade.

După ce ne dăm seama că o anumită rată de creștere exponențială ne poate duce de la 1 la i, creșterea acestei rate nu face decât să ne rotească și mai mult. Nu vom scăpa niciodată din cerc.

Cu toate acestea, dacă rata noastră de creștere este complexă (a+bi vs Ri), atunci partea reală (a) ne va crește ca de obicei, în timp ce partea imaginară (bi) ne rotește. Dar haideți să nu devenim pretențioși: Formula lui Euler, $e^{ix}$, se referă la creșterea pur imaginară care ne menține pe cerc (mai multe mai târziu).

O scurtă verificare a sănătății mintale

În timp ce scriam, a trebuit să-mi clarific câteva întrebări:

De ce să folosim $e^x$, nu rotim numărul 1?

e reprezintă procesul de a începe de la 1 și de a crește continuu cu o dobândă de 100% timp de 1 unitate de timp.

Când scriem e, capturăm întregul proces într-un singur număr – e reprezintă toată tevatura de creștere continuă. Deci, de fapt, $e^x$ spune „începe de la 1 și crește continuu la 100% timp de x secunde”, și începe de la 1, așa cum ne dorim.

Dar ce face i ca exponent?

Pentru un exponent obișnuit ca $3^4$ ne întrebăm:

• Care este rata de creștere implicită? Crescem de la 1 la 3 (baza exponentului).
• Cum schimbăm această rată de creștere? O scalăm cu 4x (puterea exponentului).

Putem converti creșterea noastră în format „e”: rata noastră instantanee este ln(3) și o creștem la ln(3) * 4. Din nou, puterea exponentului (4) tocmai a scalat rata noastră de creștere.

Când exponentul superior este i (ca în $3^i$), pur și simplu înmulțim rata noastră de creștere implicită cu i. Deci, în loc să creștem la vechea rată de creștere ln(3), creștem la ln(3) * i.

Partea de sus a exponentului modifică rata de creștere implicită a părții de jos.

Detalii amănunțite

Să aruncăm o privire mai atentă. Amintiți-vă această definiție a lui e:

Cel $\frac{100\%}{n}$ reprezintă partea de dobândă pe care am câștigat-o în fiecare perioadă microscopică. Am presupus că rata dobânzii a fost de 100% în dimensiunea reală – dar ce s-ar întâmpla dacă ar fi 100% în direcția imaginară?

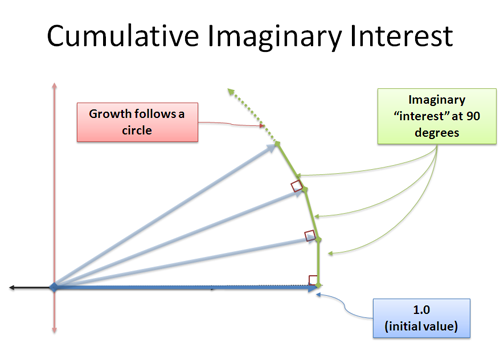
Acum, dobânda noastră nou formată se adaugă la noi în direcția de 90 de grade. În mod surprinzător, acest lucru nu ne schimbă lungimea – acesta este un concept înșelător, deoarece pare să facă un triunghi în care ipotenuza trebuie să fie mai mare. Avem de-a face cu o limită, iar distanța suplimentară se află în marja de eroare pe care o specificăm. Acesta este un subiect pe care vreau să îl abordez într-o altă zi, dar credeți-mă pe cuvânt: creșterea perpendiculară continuă vă va roti. Aceasta este inima sinusului și a cosinusului, unde schimbarea este perpendiculară pe poziția voastră curentă și vă deplasați în cerc.

Aplicăm i unități de creștere în creșteri infinit de mici, fiecare împingându-ne la un unghi de 90 de grade. Nu există o rotație „din ce în ce mai rapidă” – în schimb, ne târâm de-a lungul perimetrului pe o distanță de |i| = 1 (mărimea lui i).

Și hei — distanța târâtă în jurul unui cerc este un unghi în radiani! Am găsit o altă modalitate de a descrie mișcarea circulară!

Pentru a obține mișcarea circulară: Schimbați continuu prin rotație la un unghi de 90 de grade (aka rata de creștere imaginară).

Deci, formula lui Euler spune „creșterea exponențială, imaginară trasează un cerc”. Iar această traiectorie este aceeași cu deplasarea într-un cerc folosind sinus și cosinus în planul imaginar.

În acest caz, cuvântul „exponențial” este confuz, deoarece ne deplasăm în jurul cercului cu o rată constantă. În majoritatea discuțiilor, se presupune că creșterea exponențială are un efect cumulativ, compus.

Câteva exemple

Nu mă crezi cu adevărat, nu-i așa? Iată câteva exemple și cum să te gândești la ele în mod intuitiv.

Exemplu: $e^i$

Unde este x? Ah, este doar 1. Intuitiv, fără să scoatem un calculator, știm că asta înseamnă „parcurge 1 radian de-a lungul cercului unitar”. În capul meu, îl văd pe „e” încercând să crească 1 la 100% tot în aceeași direcție, dar i continuă să miște mingea și îl forțează pe „1” să crească de-a lungul marginii unui cerc:

Nu este cel mai frumos număr, dar iată-l. Nu uitați să vă puneți calculatorul în modul radian atunci când îl introduceți.

Exemplu: $3^i$

Acest lucru este complicat – nu este în formatul nostru standard. Dar țineți minte,

Vrem o creștere inițială de 3x la sfârșitul perioadei, sau o rată instantanee de ln(3). Dar, vine i și schimbă acea rată de ln(3) în „i * ln(3)”:

Credeam că ne vom transforma la o rată regulată de ln(3), puțin mai rapidă decât o creștere continuă de 100%, deoarece e este de aproximativ 2,718. Dar oh nu, i-am învârtit: acum ne transformăm cu o rată imaginară, ceea ce înseamnă că doar ne rotim în jurul. Dacă i ar fi fost un număr regulat, cum ar fi 4, ne-ar fi făcut să creștem de 4 ori mai repede. Acum creștem cu o viteză de ln(3), dar în lateral.

Ar trebui să ne așteptăm la un număr complex pe cercul unitar – nu există nimic în rata de creștere care să ne mărească dimensiunea. Rezolvarea ecuației:

Atunci, în loc să ajungem cu „1” unitate în jurul cercului (ca $e^i$) ajungem cu ln(3) unități în jur.

Exemplu: $i^i$

Cu câteva luni în urmă, acest lucru m-ar fi făcut să plâng. Nu și astăzi! Să descompunem transformările:

Începem cu 1 și vrem să îl modificăm. Cum ar fi să rezolvăm $3^i$, care este rata de creștere instantanee reprezentată de i ca bază?

Hrm. În mod normal, am face ln(x) pentru a obține rata de creștere necesară pentru a ajunge la x la sfârșitul a 1 unitate de timp. Dar pentru o rată imaginară? Trebuie să mai tărăgănăm asta.

Pentru a începe cu 1 și a crește până la i, trebuie să începem să ne rotim de la început. Cât de repede? Ei bine, trebuie să obținem 90 de grade (pi/2 radiani) în 1 unitate de timp. Deci, rata noastră este $i \frac{\pi}{2}$. Amintiți-vă că rata noastră trebuie să fie imaginară, deoarece ne rotim, nu creștem! Vechea $\frac{\pi}{2}$ este de aproximativ 1,57 și are ca rezultat o creștere regulată.

Acest lucru ar trebui să aibă sens: pentru a transforma 1,0 în i la sfârșitul unei unități, ar trebui să rotim $\frac{\pi}{2}$ radiani (90 de grade) în acest interval de timp. Așadar, pentru a obține „i” putem folosi $e^{i \frac{\pi}{2}}$.

Phew. Asta descrie i ca bază. Cum rămâne cu exponentul?

Bine, celălalt i ne spune să ne schimbăm rata – da, acea rată pe care am petrecut atât de mult timp să o calculăm! Deci, mai degrabă decât să ne rotim cu o viteză de $i \frac{\pi}{2}$, ceea ce înseamnă o bază de i, transformăm rata în:

I-urile se anulează și fac ca rata de creștere să fie din nou reală! Am rotit rata noastră și ne-am împins în numere negative. Iar o rată de creștere negativă înseamnă că ne micșorăm – ar trebui să ne așteptăm ca $i^i$ să facă lucrurile mai mici. Și așa este:

Tada! (Căutați „i^i” pe Google pentru a folosi calculatorul său)

Rezuflați: Vă puteți da seama intuitiv cum ar trebui să se comporte bazele imaginare și exponenții imaginari. Uau.

Și, ca bonus, v-ați dat seama de ln(i) – pentru a face ca $e^x$ să devină i, faceți ca e să se rotească cu $\frac{\pi}{2}$ radiani.

Exemplu: (i^i)^i

Un exponent imaginar dublu? Dacă insistați. În primul rând, știm care va fi rata noastră de creștere în interiorul parantezei:

Obținem o rată de creștere negativă (de micșorare) de -pi/2. Și acum modificăm din nou această rată cu i:

Și acum avem o rotație negativă! Ne deplasăm în jurul cercului cu o rată de $-\frac{\pi}{2}$ pe unitate de timp. Cât timp mergem? Ei bine, există o unitate de timp implicită „1” în partea de sus a acestui lanț de exponenți; implicit, valoarea implicită este de a merge pentru 1 unitate de timp (la fel ca $e = e^1$). 1 unitate de timp ne dă o rotație de $-\frac{\pi}{2}$ radiani (-90 de grade) sau -i!

Și, ca să ne distrăm, dacă ridicăm la pătrat acest rezultat nebunesc:

Este „doar” de două ori mai mare decât rotația: 2 este un număr regulat, așa că ne dublează rata de rotație la un total de -180 de grade într-o unitate de timp. Sau, o puteți privi ca și cum ați aplica o rotație de -90 de grade de două ori la rând.

La prima vedere, aceștia sunt exponenți foarte ciudați. Dar cu ajutorul analogiilor noastre le putem lua cu ușurință.

Creștere complexă

Potem avea creștere reală și imaginară în același timp: partea reală ne scalează în sus, iar partea imaginară ne rotește:

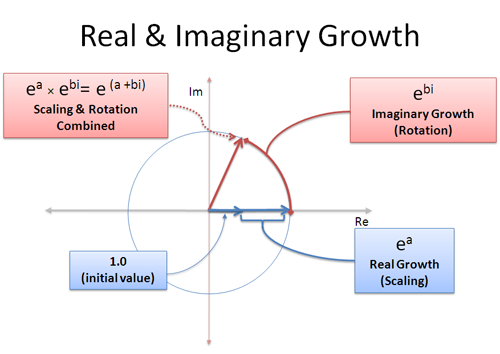
O rată de creștere complexă precum (a + bi) este un amestec de creștere reală și imaginară. Partea reală a, înseamnă „crește la 100% timp de a secunde”, iar partea imaginară b înseamnă „se rotește timp de b secunde”. Țineți minte, rotațiile nu beneficiază de avantajul compunerii, deoarece continuați să „împingeți” într-o direcție diferită – rotația se adună liniar.

Cu acest lucru în minte, putem reprezenta orice punct de pe orice cerc de orice dimensiune folosind (a+bi)! Raza este $e^a$, iar unghiul este determinat de $e^{bi}$. Este ca și cum am pune numărul în expand-o-tron pentru două cicluri: o dată pentru a-l crește la dimensiunea potrivită (a secunde), altă dată pentru a-l roti la unghiul potrivit (b secunde). Sau, ai putea să-l rotești mai întâi și apoi să-l crești!

Să spunem că vrem să știm cantitatea de creștere pentru a ajunge la 6 + 8i. Acest lucru cere de fapt logaritmul natural al unui număr imaginar: cum creștem e pentru a obține (6 + 8i)?

• Radiu: Cât de mare este cercul de care avem nevoie? Ei bine, mărimea este $\sqrt{6^2 + 8^2} = \sqrt{100} = 10$. Ceea ce înseamnă că trebuie să creștem timp de ln(10) = 2,3 secunde pentru a ajunge la această sumă.
• Cantitatea de rotit: Care este unghiul din acel punct? Putem folosi arctanul pentru a ne da seama: atan(8/6) = 53 de grade = 0,93 radian.
• Combinați rezultatul: ln(6+8i) = 2,3 + 0,93i

Acest lucru înseamnă că putem ajunge la punctul aleatoriu (6 + 8i) dacă folosim $e^{2.3 + .93i}$.

De ce este aceasta utilă?

Formula lui Euler ne oferă o altă modalitate de a descrie mișcarea într-un cerc. Dar am putea face deja acest lucru cu sinus și cosinus – ce este atât de special?

Este vorba de perspectivă. Sinusul și cosinusul descriu mișcarea în termenii unei grile, trasând coordonate orizontale și verticale.

Formula lui Euler folosește coordonate polare — care este unghiul și distanța ta? Din nou, sunt două moduri de a descrie mișcarea:

• Sistemul grilă: Mergi 3 unități spre est și 4 unități spre nord
• Coordonate polare: Mergi 5 unități la un unghi de 53,13 grade

În funcție de problemă, coordonatele polare sau rectangulare sunt mai utile. Formula lui Euler ne permite să facem conversia între cele două pentru a folosi cel mai bun instrument de lucru. De asemenea, deoarece $e^{ix}$ poate fi convertit în sinus și cosinus, putem rescrie formulele din trigonometrie ca variații ale lui e, ceea ce este foarte util (nu este nevoie să memorați sin(a+b), puteți să o derivați – mai multe într-o altă zi). Și este frumos că fiecare număr, real sau complex, este o variație a lui e.

Dar utilitate, schmutilitate: cel mai important rezultat este conștientizarea faptului că ecuațiile derutante pot deveni intuitive cu analogiile potrivite. Nu lăsați ca ecuațiile frumoase, cum ar fi formula lui Euler, să rămână o vrajă magică – construiți pe baza analogiilor pe care le cunoașteți pentru a vedea intuițiile din interiorul ecuației.

Matematică fericită.

Apendice

Screencast-ul a fost distractiv, iar feedback-ul este cu siguranță binevenit. Cred că ajută ideile să iasă în evidență, iar parcurgerea articolului m-a ajutat să găsesc lacune în intuiția mea.

• Brian Slesinsky are o prezentare îngrijită despre formula lui Euler
• Visual Complex Analysis are o discuție grozavă despre formula lui Euler – a se vedea p. 10 în Google Book Preview
• Am făcut o prezentare la Math and Analogies care explică identitatea lui Euler mai vizual:

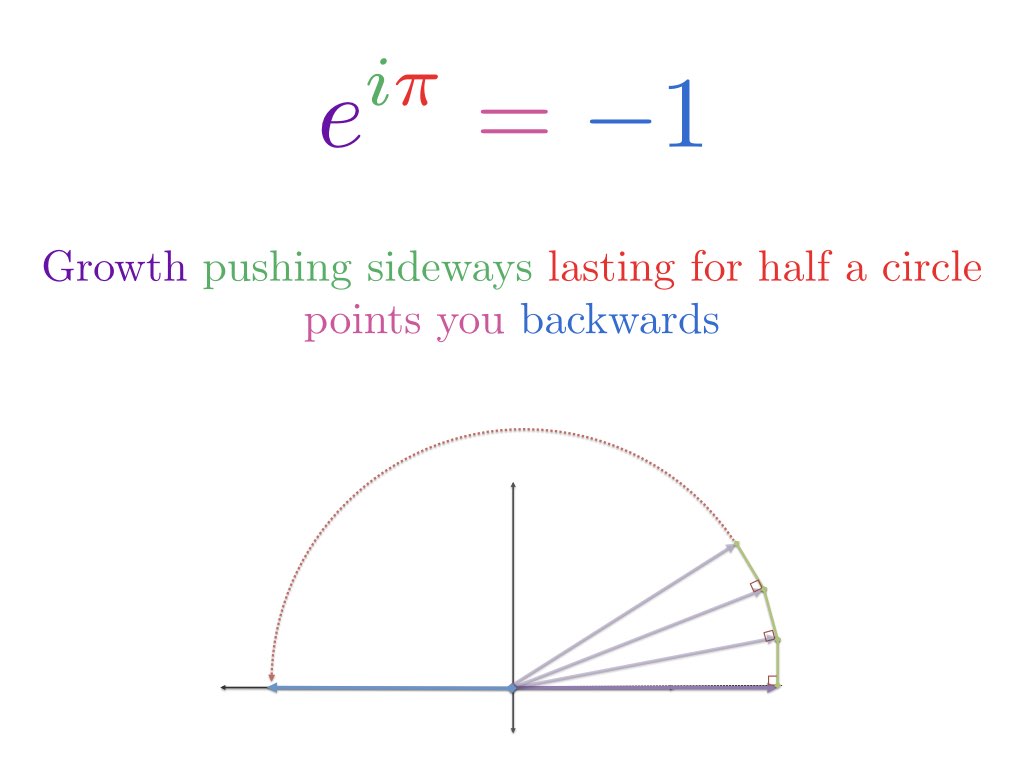
Alte postări din această serie

1. Un ghid vizual, intuitiv al numerelor imaginare
2. Aritmetică intuitivă cu numere complexe
3. Înțelegând de ce funcționează înmulțirea complexă
4. Ghid intuitiv al unghiurilor, grade și radiani
5. Înțelegerea intuitivă a formulei lui Euler
6. Un ghid interactiv al transformării Fourier
7. Ghid intuitiv al convoluției
8. Ghid intuitiv al convoluției

.

9. Înțelegerea intuitivă a undelor sinusoidale
10. Un ghid intuitiv de algebră liniară
11. Intuiția unui programator pentru înmulțirea matricelor
12. Înțelegerea intuitivă a înmulțirii matricelor
13. Înmulțirea imaginară vs. înmulțirea imaginară. Exponenți imaginari