Obiective de învățare
- Înțelegerea reprezentării 3D a orbitalilor electronici
Un orbital este rafinamentul mecanic cuantic al orbitei lui Bohr. Spre deosebire de conceptul său de orbită simplă circulară\(r\) cu o rază fixă, orbitalii sunt regiuni ale spațiului derivate matematic, cu probabilități diferite de a conține un electron.
Un mod de a reprezenta distribuțiile de probabilitate ale electronilor a fost ilustrat anterior pentru orbitalul 1s al hidrogenului. Deoarece Ψ2 dă probabilitatea de a găsi un electron într-un anumit volum de spațiu (cum ar fi un picometru cubic), o reprezentare grafică a lui Ψ2 în funcție de distanța față de nucleu (r) este o reprezentare grafică a densității de probabilitate. Orbitalul 1s este sferic simetric, astfel încât probabilitatea de a găsi un electron 1s în orice punct dat depinde doar de distanța acestuia față de nucleu. Densitatea de probabilitate este cea mai mare la \(\(r\) = 0\) (la nucleu) și scade în mod constant odată cu creșterea distanței. La valori foarte mari ale lui r, densitatea de probabilitate a electronului este foarte mică, dar nu nulă.
În schimb, putem calcula probabilitatea radială (probabilitatea de a găsi un electron 1s la o distanță \(r\) față de nucleu) prin însumarea în același timp\(r\) a probabilităților ca un electron să se afle în toate punctele unei serii de x învelișuri sferice de rază r1, r2, r3,…, rx – 1, rx. De fapt, împărțim atomul în învelișuri concentrice foarte subțiri, la fel ca straturile unei cepe (Figura \(\PageIndex{1a}\)), și calculăm probabilitatea de a găsi un electron pe fiecare înveliș sferic. Reamintim că densitatea de probabilitate a electronilor este cea mai mare la \(r\) = 0 (Figura \(\(\PageIndex{1b}\)), astfel încât densitatea de puncte este cea mai mare pentru \(r\) cele mai mici cochilii sferice din partea (a) din Figura \(\PageIndex{1}\). În schimb, suprafața fiecărei cochilii sferice este egală cu \(4πr^2\), care crește foarte rapid odată cu creșterea \(r\) (Figura \(\PageIndex{1c}\)). Deoarece suprafața învelișurilor sferice crește mai rapid odată cu creșterea \(r\) decât scade densitatea de probabilitate a electronilor, graficul probabilității radiale are un maxim la o anumită distanță\(r\) (Figura \(\PageIndex{1d}\)). Cel mai important, atunci când \(r\) este foarte mică, suprafața unui înveliș sferic este atât de mică încât probabilitatea totală de a găsi un electron în apropierea nucleului este foarte scăzută; la nucleu, probabilitatea electronului dispare (Figura \(\PageIndex{1d}\)).

Fo(r\) atomul de hidrogen, vârful din graficul probabilității radiale apare la \(r\) = 0,529 Å (52,9 pm), care este exact raza calculată de Boh\(r\) fo\(r\) pentru orbita n = 1. Astfel, raza cea mai probabilă obținută din mecanica cuantică este identică cu raza calculată de mecanica clasică. Cu toate acestea, în modelul lui Bohr, s-a presupus că electronul se află la această distanță 100% din timp, în timp ce în modelul Schrödinge\(r\), el se află la această distanță doar o parte din timp. Diferența dintre cele două modele poate fi atribuită comportamentului ondulatoriu al electronului și principiului de incertitudine Heisenberg.
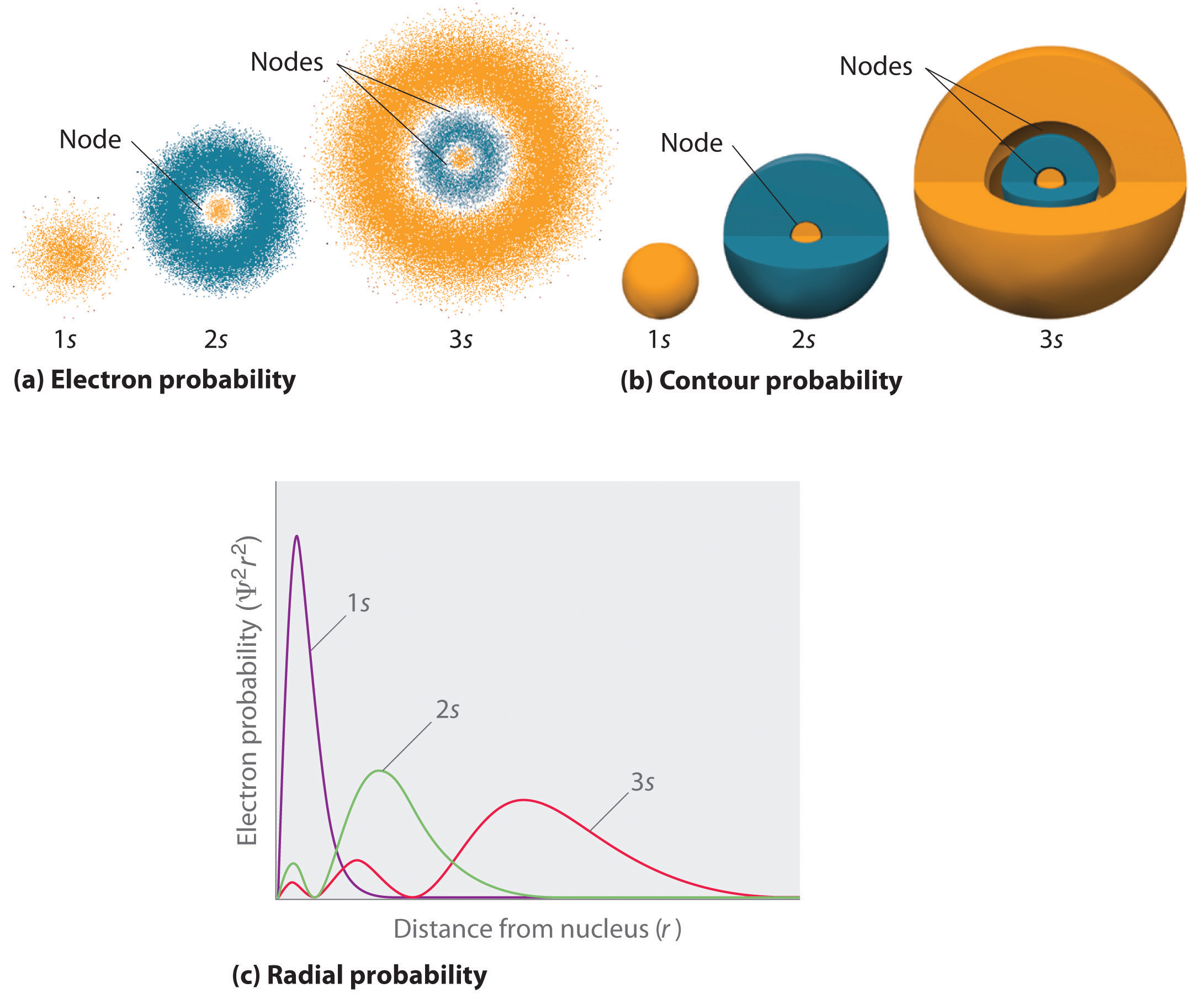
Figura \(\PageIndex{2}\) compară densitățile de probabilitate ale electronilor pentru orbitalele 1s, 2s și 3s ale hidrogenului. Observați că toți trei sunt sferic simetrici. Pentru orbitalii 2s și 3s, totuși (precum și pentru toți ceilalți orbitali s), densitatea de probabilitate a electronilor nu scade lin odată cu creșterea \(r\\). În schimb, se observă o serie de minime și maxime în diagramele de probabilitate radială (Figura \(\(\PageIndex{2c}\)). Minimele corespund nodurilor sferice (regiuni de probabilitate zero a electronilor), care alternează cu regiuni sferice de probabilitate diferită de zero a electronilor. Existența acestor noduri este o consecință a schimbărilor de fază de undă în funcția de undă Ψ.
Orbitalii s (l=0)
Trei lucruri se întâmplă cu orbitalii s pe măsură ce n crește (Figura \(\PageIndex{2}\)):
- Devin mai mari, extinzându-se mai departe\(r\) de nucleu.
- Conțin mai multe noduri. Acest lucru se aseamănă cu o undă staționară care are regiuni de amplitudine semnificativă separate de noduri, puncte cu amplitudine zero.
- Pentru un atom dat, orbitalii s devin, de asemenea, mai mari în energie pe măsură ce n crește, din cauza distanței crescute față de nucleu.
Orbitalele sunt în general desenate ca suprafețe tridimensionale care înglobează 90% din densitatea de electroni, așa cum s-a arătat pentru orbitalele 1s, 2s și 3s ale hidrogenului în partea (b) din figura \(\PageIndex{2}\). Deși astfel de desene arată dimensiunile relative ale orbitalilor, ele nu arată în mod normal nodurile sferice din orbitalii 2s și 3s, deoarece nodurile sferice se află în interiorul suprafeței de 90%. Din fericire, pozițiile nodurilor sferice nu sunt importante pentru legăturile chimice fo\(r\).
Orbitalii p (l=1)
Doar orbitalii s sunt sferic simetrici. Pe măsură ce crește valoarea lui l, crește numărul\(r\) de orbitali dintr-o anumită subshell, iar formele orbitalilor devin mai complexe. Deoarece subshell-ul 2p are l = 1, cu trei valori ale lui ml (-1, 0 și +1), există trei orbitali 2p.
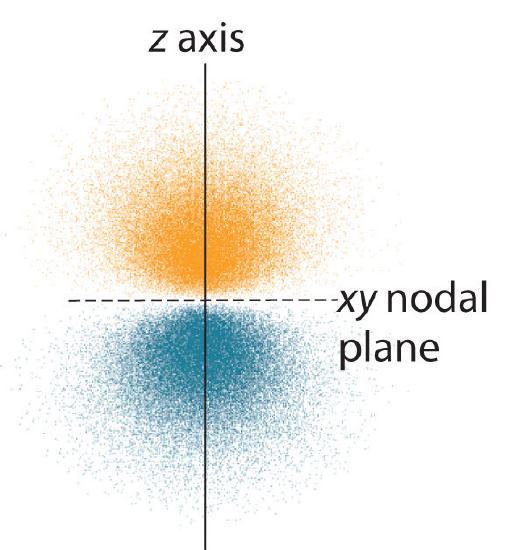
Distribuția de probabilitate a electronilor fo\(r\) unul dintre orbitalii 2p ai hidrogenului este prezentată în figura \(\PageIndex{3}\). Deoarece acest orbital are doi lobi de densitate de electroni dispuși de-a lungul axei z, cu o densitate de electroni egală cu zero în planul xy (adică planul xy este un plan nodal), este un orbital \(2p_z\). După cum se arată în figura \(\(\PageIndex{4}\), ceilalți doi orbitali 2p au forme identice, dar sunt așezați de-a lungul axei x (\(2p_x\)) și, respectiv, a axei y (\(2p_y\)). Rețineți că fiecare orbital p are doar un singur plan nodal. În fiecare caz, faza funcției de undă fo\(r\) a fiecăruia dintre orbitalii 2p este pozitivă fo\(r\) pentru lobul care punctează de-a lungul axei pozitive și negativă fo\(r\) pentru lobul care punctează de-a lungul axei negative. Este important de subliniat că aceste semne corespund fazei undei care descrie mișcarea electronului, nu sarcinilor pozitive o\(r\) negative.
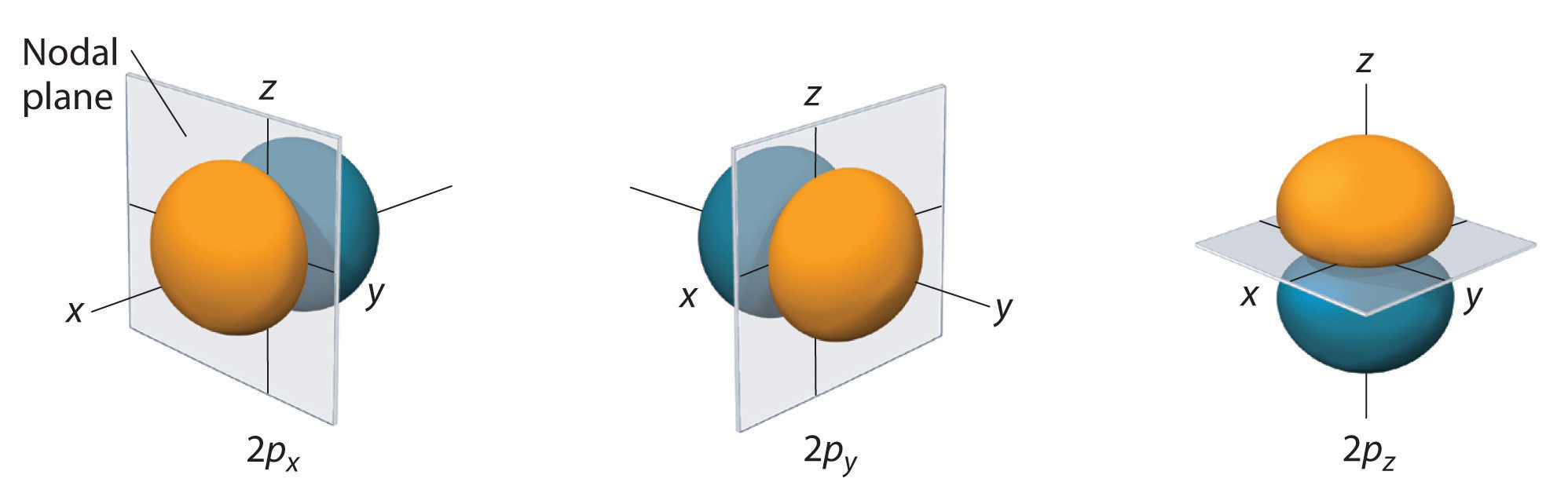
Suprafețele arătate cuprind 90% din probabilitatea totală a electronilor fo\(r\) orbitalii 2px, 2py și 2pz. Fiecare orbital este orientat de-a lungul axei indicate de indice și un plan nodal care este perpendicular pe această axă bisectează fiecare orbital 2p. Faza funcției de undă este pozitivă (portocalie) în regiunea spațială în care x, y, o\(r\) z este pozitivă și negativă (albastră) în regiunea în care x, y, o\(r\) z este negativă. La fel ca în cazul orbitalilor s, dimensiunea și complexitatea orbitalilor p fo\(r\) oricărui atom cresc pe măsură ce crește numărul cuantic principal n. Cu toate acestea, formele suprafețelor de probabilitate de 90% ale orbitalilor 3p, 4p și ale orbitalilor p de energie mai mare sunt, în esență, aceleași cu cele prezentate în figura \(\PageIndex{4}\).
Orbitalii d (l=2)
Subshell-urile cu l = 2 au cinci orbitali d; primul shell principal care are un subshell d corespunde la n = 3. Cei cinci orbitali d au valorile ml de -2, -1, 0, +1 și +2.
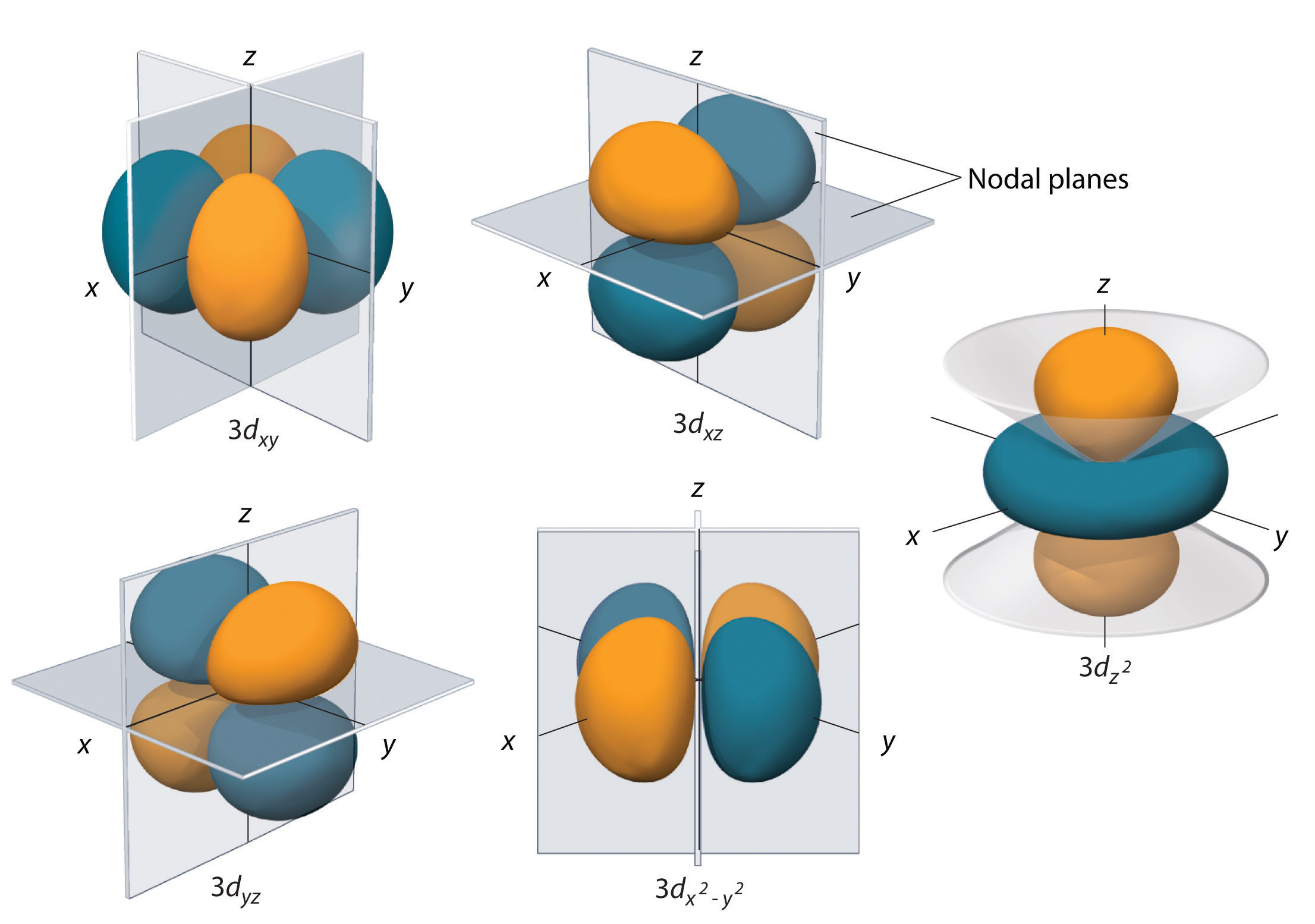
Orbitalele 3d ale hidrogenului, prezentate în figura \(\PageIndex{5}\), au forme mai complexe decât orbitalii 2p. Toți cei cinci orbitali 3d conțin două suprafețe nodale, în comparație cu unul fo\(r\) pentru fiecare orbital p și zero fo\(r\) pentru fiecare orbital s. În trei dintre orbitalii d, lobii densității electronice sunt orientați între planurile x și y, x și z și y și z; acești orbitali sunt denumiți orbitalii \(3d_{xy}\), \)3d_{xz}\) și, respectiv, \(3d_{yz}\). Un al patrulea orbital d are lobi situați de-a lungul axelor x și y; acesta este orbitalul \(3d_{x^2-y^2}\). Al cincilea orbital 3d, numit orbitalul \(3d_{z^2}\), are o formă unică: arată ca un orbital \(2p_z\) combinat cu o gogoașă suplimentară de probabilitate electronică situată în planul xy. În ciuda formei sale ciudate, orbitalul \(3d_{z^2}\) este echivalent din punct de vedere matematic cu celălalt \(r\) fou\(r\) și are aceeași energie. Spre deosebire de orbitalii p, faza funcției de undă pentru orbitalii d este aceeași pentru perechile opuse de lobi. Așa cum se arată în figura \(\(\PageIndex{5}\), faza funcției de undă este pozitivă fo\(r\) cei doi lobi ai orbitalului \(dz^2\) care se află de-a lungul axei z, în timp ce faza funcției de undă este negativă fo\(r\) gogoașa densității de electroni din planul xy. Ca și în cazul orbitalilor s și p, pe măsură ce n crește, mărimea orbitalilor d crește, dar formele generale rămân simila\\(r\) cu cele reprezentate în figura \(\PageIndex{5}\).
f Orbitalii (l=3)
Învelișurile principale cu n = 4 pot avea subînvelișuri cu l = 3 și valori ml de -3, -2, -1, 0, +1, +2 și +3. Aceste subshell-uri sunt formate din șapte orbitali f. Fiecare orbital f are trei suprafețe nodale, astfel încât formelei\(r\) sunt complexe. Deoarece orbitalii f nu sunt deosebit de importanți pentru scopurile noastre, nu îi discutăm în continuare, iar orbitalii cu valori mai mari ale lui l nu sunt discutați deloc.
Energii orbitale
Deși am discutat formele orbitalilor, am spus puține lucruri despre energiile comparativei\(r\\). Începem discuția noastră despre energiile orbitalilor luând în considerare atomii sau ionii cu un singur electron (cum ar fi H sau He+).
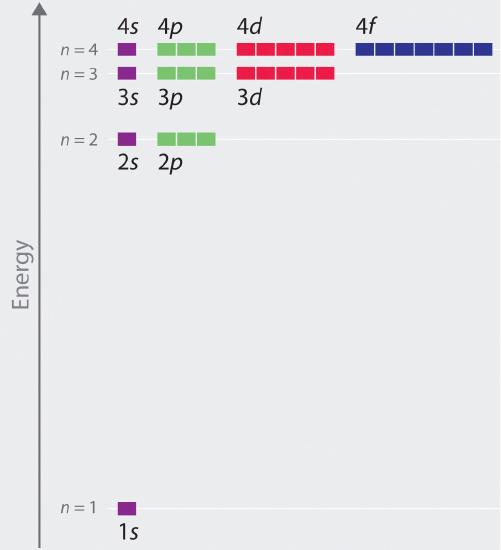
Energii relative ale orbitalilor atomici cu n ≤ 4 pentru un atom de hidrogen sunt reprezentate în figura \(\PageIndex{6}\); rețineți că energiile orbitalilor depind doar de numărul cuantic principal n. În consecință, energiile orbitalilor 2s și 2p ai hidrogenului sunt aceleași; energiile orbitalilor 3s, 3p și 3d sunt aceleași; și așa mai departe. Mecanica cuantică prezice că, în atomul de hidrogen, toți orbitalii cu aceeași valoare a lui n (de exemplu, cei trei orbitali 2p) sunt degenerate, ceea ce înseamnă că au aceeași energie. Energiile orbitale obținute pentru hidrogenul fo\(r\) folosind mecanica cuantică sunt exact aceleași cu energiile permise calculate de Boh\(r\). Spre deosebire însă de modelul lui Bohr, care permitea un singur orbital fo\(r\) pentru fiecare nivel energetic, mecanica cuantică prezice că există 4 orbitali cu distribuții diferite ale densității electronice în învelișul principal n = 2 (un orbital 2s și trei 2p), 9 în învelișul principal n = 3 și 16 în învelișul principal n = 4.Valorile diferite ale lui l și ml pentru orbitalii individuali din cadrul unui anumit înveliș principal nu sunt importante pentru înțelegerea spectrelor de emisie sau de absorbție ale atomului de hidrogen în majoritatea condițiilor, dar ele explică separările liniilor principale care sunt observate atunci când atomii de hidrogen sunt plasați într-un câmp magnetic. Figura \(\(\PageIndex{6}\) arată că nivelurile de energie devin apropiate\(r\) și apropiate\(r\) între ele\(r\) pe măsură ce valoarea lui n crește, așa cum era de așteptat datorită dependenței 1/n2 a energiilor orbitale.
Energia orbitalilor în orice specie cu un singur electron poate fi calculată printr-o variație mino\(r\) a ecuației lui Bohr, care poate fi extinsă la alte specii cu un singur electron prin încorporarea sarcinii nucleului \(Z\) (numărul\(r\) de protoni din nucleu):
\
În general, atât energia cât și raza scad pe măsură ce crește sarcina nucleară (r\(r\)). Astfel, cei mai stabili orbitali (cei cu cea mai mică energie) sunt cei mai apropiați de nucleu. Fo\(r\\) exemplu, în starea fundamentală a atomului de hidrogen, un singur electron se află pe orbitalul 1s, în timp ce în prima stare excitată, atomul a absorbit energie și electronul a fost promovat pe unul dintre orbitalii n = 2. În cazul ionilor cu un singur electron, energia unui anumit orbital depinde numai de n, iar toate subînvelișurile din cadrul unui înveliș principal, cum ar fi orbitalii \(p_x\), \(p_y\) și \(p_z\), sunt degenerate.
Rezumat
Tipurile de orbitali atomici importanți din punct de vedere chimic fou\(r\) corespund valorilor \(\ell = 0\), \(1\), \(2\) și \(3\). Orbitalii cu \(\ell = 0\) sunt orbitali s și sunt sferic simetrici, cu cea mai mare probabilitate de a găsi electronul în nucleu. Toți orbitalii cu valorile \(n > 1\) și \(ell = 0\) conțin mai multe noduri o\(r\). Orbitalii cu \(\ell = 1\) sunt orbitali p și conțin un plan nodal care include nucleul, dând naștere la o formă de halteră. Orbitalii cu \(\ell = 2\) sunt orbitali d și au forme mai complexe, cu cel puțin două suprafețe nodale. Orbitalii cu \(\ell = 3\) sunt orbitali f, care sunt și mai complecși.
Pentru că distanța medie față de nucleu determină energia unui electron, fiecărui orbital atomic cu un anumit set de numere cuantice îi este asociată o energie particulară, energia orbitalului.
\
În atomii o\(r\) ioni cu un singur electron, toți orbitalii cu aceeași valoare a lui \(n\) au aceeași energie (sunt degenerate), iar energiile învelișurilor principale cresc lin pe măsură ce \(n\) crește. Un ion atom o\(r\(r\) cu electronul (electronii) în orbitalul (orbitalii) de cea mai joasă energie se spune că se află în starea fundamentală, în timp ce un ion atom o\(r\) în care unul sau mai mulți electroni ocupă orbitali de energie mai mare se spune că se află într-o stare excitată.
Contribuții și atribuții
-
Modificat de Joshua Halpern (Howard University)
.