Ca și în cazul regulatorului P-Only, algoritmul Proporțional-Integral (PI) calculează și transmite un semnal de ieșire a regulatorului (CO) la fiecare timp de eșantionare, T, către elementul final de control (de exemplu, supapă, pompă cu viteză variabilă). CO calculat de algoritmul PI este influențat de parametrii de reglare a regulatorului și de eroarea regulatorului, e(t).
Reglatoarele PI au doi parametri de reglare. Deși acest lucru le face mai dificil de reglat decât un regulator numai P, ele nu sunt la fel de complexe ca regulatorul PID cu trei parametri.
Acțiunea integrală permite regulatorilor PI să elimine decalajul, un punct slab major al unui regulator numai P. Astfel, controlorii PI oferă un echilibru între complexitate și capacitate care îi face de departe cel mai utilizat algoritm în aplicațiile de control al proceselor.
Algoritmul PI
În timp ce diferiți vânzători prezintă ceea ce este în esență același algoritm în forme diferite, aici explorăm ceea ce este descris în diverse moduri ca fiind forma dependentă, ideală, continuă, de poziție:
![]()
Unde:
CO = semnalul de ieșire al regulatorului (ieșirea firului)
CObias = polarizarea regulatorului sau valoarea nulă; setată prin transfer fără goluri, așa cum se explică mai jos
e(t) = eroarea curentă a regulatorului, definită ca SP – PV
SP = punctul de setare
PV = variabila de proces măsurată (firul de intrare)
Kc = câștigul regulatorului, un parametru de reglare
Ti = timpul de resetare, un parametru de reglare
Primii doi termeni din dreapta semnului egal sunt identici cu regulatorul P-Only la care se face referire în partea de sus a acestui articol.
Modul integral al regulatorului este ultimul termen al ecuației. Funcția sa este de a integra sau de a însuma continuu eroarea controlerului, e(t), în timp.
Câteva lucruri pe care ar trebui să le știm despre parametrul de reglare a timpului de resetare, Ti:
| ▪ | Acesta oferă o pondere separată pentru termenul integral, astfel încât influența acțiunii integrale poate fi reglată independent. | |
| ▪ | Se află la numitor, astfel încât valorile mai mici asigură o pondere mai mare pentru (i.e. crește influența) termenului integral. | |
| ▪ | Acesta are unități de timp, astfel încât este întotdeauna pozitiv. |
Funcția termenului proporțional
Ca și în cazul regulatorului P-Only, termenul proporțional al regulatorului PI, Kc-e(t), se adaugă sau se scade din CObias în funcție de mărimea erorii regulatorului e(t) la fiecare timp t.
Cum e(t) crește sau se micșorează, cantitatea adăugată la CObias crește sau se micșorează imediat și proporțional. Istoricul trecut și traiectoria curentă a erorii controlerului nu au nicio influență asupra calculului termenului proporțional.
Tratciculul de mai jos (faceți clic pentru o vizualizare mai mare) ilustrează această idee pentru un răspuns la punctul de setare. Eroarea utilizată în calculul proporțional este indicată pe grafic:
▪ La timpul t = 25 min, e(25) = 60-56 = 4
▪ La timpul t = 40 min, e(40) = 60-62 = -2
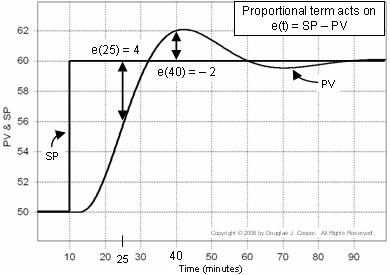
Reamintind că eroarea controlerului e(t) = SP – PV, mai degrabă decât să privim PV și SP ca urme separate, așa cum facem mai sus, putem calcula și reprezenta grafic e(t) la fiecare punct din timpul t.
Datele de mai jos (faceți clic pentru o vizualizare mai mare) sunt identice cu cele de mai sus, doar că sunt refăcute ca un traseu al lui e(t) însuși. Observați că în graficul de mai sus, PV = SP = 50 pentru primele 10 min, în timp ce în graficul de eroare de mai jos, e(t) = 0 pentru aceeași perioadă de timp.
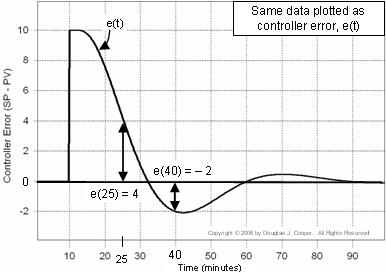
Acest grafic este util deoarece ne ajută să vizualizăm modul în care eroarea controlorului își schimbă în mod continuu mărimea și semnul pe măsură ce trece timpul.
Funcția termenului integral
În timp ce termenul proporțional ia în considerare mărimea curentă a lui e(t) doar în momentul calculării regulatorului, termenul integral ia în considerare istoricul erorii, sau cât timp și cât de departe a fost variabila de proces măsurată față de punctul de setare de-a lungul timpului.
Integrarea este o însumare continuă. Integrarea erorii în timp înseamnă că însumăm întregul istoric al erorii controlerului până în prezent, începând din momentul în care controlerul a fost comutat pentru prima dată pe automat.
Eroarea controlerului este e(t) = SP – PV. În graficul de mai jos (faceți clic pentru o vizualizare mai mare), suma integrală a erorii este calculată ca zone umbrite între urmele SP și PV.
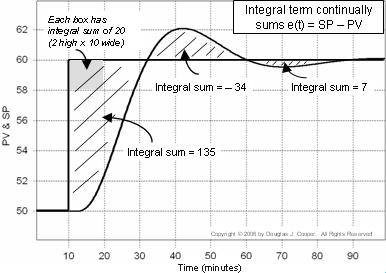
Care cutie din grafic are o sumă integrală de 20 (2 înălțime pe 10 lățime). Dacă numărăm numărul de căsuțe (inclusiv fracțiunile de căsuțe) conținute în zonele umbrite, putem calcula suma integrală a erorii.
Atunci când PV traversează pentru prima dată punctul de referință în jurul valorii de t = 32, suma integrală a crescut la aproximativ 135. Scriem termenul integral al regulatorului PI ca:
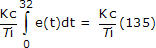
Din moment ce eroarea regulatorului este cea care conduce calculul, obținem o vizualizare directă a situației dintr-un grafic al erorii regulatorului, așa cum se arată mai jos (faceți clic pentru o vizualizare mare):

Rețineți că integrala fiecărei porțiuni umbrite are același semn ca și eroarea. Deoarece suma integrală începe să se acumuleze atunci când regulatorul este pus pentru prima dată în regim automat, suma integrală totală crește atâta timp cât e(t) este pozitivă și se micșorează atunci când este negativă.
La timpul t = 60 min pe diagrame, suma integrală este 135 – 34 = 101. Răspunsul se reglează în mare parte la t = 90 min, iar suma integrală este atunci 135 – 34 + 7 = 108.
Acțiunea integrală elimină decalajul
Firma precedentă face o observație subtilă, dar foarte importantă. Răspunsul este în mare parte complet la momentul t = 90 min, dar suma integrală a tuturor erorilor nu este zero.
În acest exemplu, suma integrală are o valoare finală sau reziduală de 108. Această valoare reziduală este cea care permite acțiunea integrală a regulatorului PI pentru a elimina decalajul.
După cum s-a discutat într-un articol anterior, cele mai multe procese aflate sub control numai P experimentează decalaj în timpul funcționării normale. Offsetul este o valoare susținută pentru eroarea controlerului (de exemplu, PV nu este egal cu SP la starea de echilibru).
Recunoaștem din controlerul P-Only:
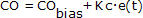
că CO va fi întotdeauna egal cu CObias, cu excepția cazului în care adăugăm sau scădem ceva din el.
Singurul mod în care avem ceva de adăugat sau de scăpat din CObias în ecuația P-Only de mai sus este dacă e(t) nu este zero. Dacă e(t) nu este constant la zero, atunci PV nu este egal cu SP și avem offset.
Cu toate acestea, cu controlerul PI:
![]()
să știm acum că suma integrală a erorilor poate avea o valoare finală sau reziduală după ce un răspuns este complet. Acest lucru este important deoarece înseamnă că e(t) poate fi zero, dar totuși putem avea ceva care să se adauge sau să se sustragă din CObias pentru a forma ieșirea finală a regulatorului, CO.
Atunci, atâta timp cât există o eroare (atâta timp cât e(t) nu este zero), termenul integral va crește sau se va micșora ca dimensiune pentru a avea un impact asupra CO. Modificările în CO vor înceta numai atunci când PV este egal cu SP (când e(t) = 0) pentru o perioadă de timp susținută.
În acel moment, termenul integral poate avea o valoare reziduală, așa cum tocmai am discutat. Această valoare reziduală din integrare, atunci când este adăugată la CObias, creează în esență o nouă valoare globală de polarizare care corespunde noului nivel de funcționare.
De fapt, acțiunea integrală resetează continuu valoarea de polarizare pentru a elimina decalajul pe măsură ce nivelul de funcționare se schimbă.
Provocările controlului PI
Există provocări în utilizarea algoritmului PI:
| ▪ | Cei doi parametri de reglare interacționează unul cu celălalt și influența lor trebuie să fie echilibrată de către proiectant. | |
| ▪ | Termenul integral tinde să crească comportamentul oscilator sau de rulare al răspunsului procesului. |
Pentru că cei doi parametri de reglaj interacționează unul cu celălalt, poate fi dificil să se ajungă la „cele mai bune” valori de reglaj. Valoarea și importanța rețetei noastre de proiectare și reglare crește pe măsură ce controlerul devine mai complex.
Inițializarea controlerului pentru transferul fără goluri
Când trecem orice controler din modul manual în cel automat (de la buclă deschisă la buclă închisă), dorim ca rezultatul să fie fără evenimente. Altfel spus, nu dorim ca trecerea să provoace acțiuni bruște de control care să aibă un impact sau să perturbe procesul nostru
Astăzi obținem acest rezultat dorit la trecere prin inițializarea sumei integrale a erorii controlerului la zero. De asemenea, punctul de setare și valoarea de polarizare a regulatorului sunt inițializate prin setarea:
▪ SP egal cu PV curent
▪ CObias egal cu CO curent
Cu suma integrală a erorii setată la zero, nu există nimic de adăugat sau de sustras din CObias care să provoace o schimbare bruscă în ieșirea curentă a regulatorului. Cu punctul de setare egal cu variabila de proces măsurată, nu există nicio eroare care să determine o modificare a CO nostru. Și cu polarizarea controlerului setată la valoarea noastră curentă de CO, suntem pregătiți în mod implicit să menținem funcționarea curentă.
Așa, când trecem de la modul manual la cel automat, avem un „transfer fără probleme”, fără surprize. Acesta este un rezultat pe care toată lumea îl apreciază.
Timp de resetare față de rata de resetare
Diferiți furnizori își prezintă algoritmii de control în forme ușor diferite. Unii folosesc banda proporțională mai degrabă decât câștigul regulatorului. De asemenea, unii folosesc rata de resetare, Tr, în loc de timpul de resetare. Aceștia sunt pur și simplu inversul unul al celuilalt:
Tr = 1/Ti
Nu contează cum sunt exprimați parametrii de reglare, algoritmii PI sunt toți la fel de capabili.
Dar este esențial să vă cunoașteți producătorul înainte de a începe reglarea regulatorului, deoarece valorile parametrilor trebuie să se potrivească cu forma particulară a algoritmului dumneavoastră.Un software comercial pentru proiectarea și reglarea regulatorului va rezolva automat această problemă pentru dumneavoastră.
Implementarea unui regulator PI
Explorăm proiectarea, reglarea și implementarea regulatorului PI pe schimbătorul de căldură în acest articol și pe rezervoarele drenate prin gravitație în acest articol.
.