O asimptotă este o dreaptă de care un grafic se apropie, dar nu se intersectează.
În această lecție, vom învăța cum să găsim asimptote verticale, asimptote orizontale și asimptote oblice (înclinate) ale funcțiilor raționale.
Subiecte conexe:
Mai multe lecții de calcul

Diagrama următoare prezintă diferitele tipuri de asimptote: asimptote orizontale, asimptote verticale și asimptote oblice. Derulați în josul paginii pentru mai multe exemple și soluții cu privire la modul de găsire a asimptotelor.

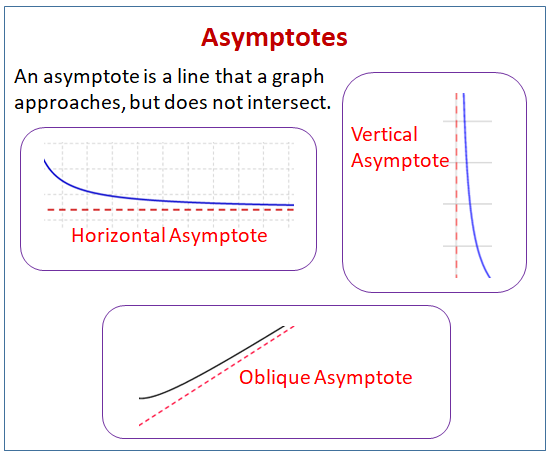
Cum se determină asimptota verticală?

Metoda 1: Folosiți definiția asimptotei verticale

Dreapta x = a se numește asimptotă verticală a curbei y = f(x) dacă cel puțin una dintre următoarele afirmații este adevărată.

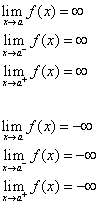
Metoda 2:

Pentru funcțiile raționale, asimptotele verticale sunt drepte verticale care corespund zerourilor numitorului.
Dată funcția rațională, f(x)

Pasul 1: Scrieți f(x) în formă redusă

Pasul 2: dacă x – c este un factor la numitor atunci x = c este asimptota verticală.

Exemplu:

Căutați asimptotele verticale ale lui

Soluție:

Căutați asimptotele verticale ale lui

:

Metoda 1: Folosiți definiția asimptotei verticale.

Dacă x este apropiat de 3, dar mai mare decât 3, atunci numitorul x – 3 este un număr pozitiv mic și 2x este apropiat de 8. Deci, este un număr mare pozitiv.

Intuitiv, vedem că

În mod similar, dacă x este apropiat de 3 dar mai mic decât 3, atunci x – 3 este un număr mic negativ și 2x este apropiat de 8. Deci, este un număr negativ mare.

Dreapta x = 3 este asimptota verticală.

Metoda 2:

Etapa 1: f(x) este deja în formă redusă.

Etapa 2: Numitorul este x – 3, deci asimptota verticală este la x = 3.

Cercetarea asimptotelor verticale ale funcțiilor raționale

Ce trebuie să căutăm, pentru a găsi asimptotele verticale ale funcțiilor raționale.

• Arată soluțiile pas cu pas

Asimptotele verticale ale funcțiilor raționale: Mod rapid de a le găsi

Exemplu de găsire a asimptotelor verticale ale funcțiilor raționale.

• Show Step-by-step Solutions

Cum se găsesc asimptotele verticale ale funcțiilor raționale

• Show Step-by-step Solutions

Cum se determină asimptota orizontală?

Metoda 1: Utilizați definiția asimptotei orizontale

Dreapta y = L se numește asimptotă orizontală a curbei y = f(x) dacă fie

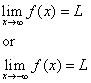
Metoda 2:

Pentru funcția rațională, f(x)

Dacă gradul lui x de la numărător este mai mic decât gradul lui x de la numitor, atunci y = 0 este asimptota orizontală.

Dacă gradul lui x din numitor este egal cu gradul lui x din numitor atunci y = c unde c se obține prin împărțirea coeficienților inițiali.

Exemplu:

Căutați asimptotele orizontală și verticală ale funcției.

Soluție:

Metoda 1:

Dividați atât numărătorul cât și numitorul cu x.

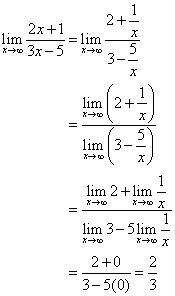
Dreapta este asimptota orizontală.

Metoda 2:

Gradul lui x din numitor este egal cu gradul lui x din numitor.

Divizând coeficienții inițiali obținem

Dreapta este asimptota orizontală.

Shortcut pentru a găsi asimptotele orizontale ale funcțiilor raționale

Câteva trucuri care fac ca găsirea asimptotelor orizontale ale funcțiilor raționale să fie foarte ușor de făcut

• Show Step-by-step Solutions

Acest videoclip va oferi o prezentare generală de bază a asimptotelor orizontale. Vom determina dacă funcțiile raționale date au asimptote orizontale și care sunt acestea.

• Show Step-by-step Solutions

Acest videoclip va intra în detalii suplimentare despre regulile asimptotelor orizontale.

• Show Step-by-step Solutions

Asimptota oblică sau asimptota oblică

Câteva curbe au asimptote care sunt oblice, adică nici orizontale, nici verticale.

Dacă atunci dreapta y = mx + b se numește asimptotă oblică sau oblică, deoarece distanțele verticale dintre curba y = f(x) și dreapta y = mx + b se apropie de 0.

Pentru funcțiile raționale, asimptotele oblice apar atunci când gradul numitorului este cu unul mai mare decât gradul numitorului. Într-un astfel de caz, ecuația asimptotei oblice poate fi găsită prin împărțire lungă.

Exemplu:

Găsește asimptotele funcției

Soluție:

Căutați asimetriile funcției

:

Din moment ce numitorul x2 + 1 nu este niciodată 0, nu există asimptotă verticală.

Din moment ce gradul lui x din numitor este mai mare decât gradul lui x din numitor nu există asimptotă orizontală.

Din moment ce gradul lui x din numitor este cu unu mai mare decât gradul lui x din numitor putem folosi împărțirea lungă pentru a obține asimptota oblică.

Deci, dreapta y = x este asimptota oblică.

Căutarea asimptotelor oblice ale funcțiilor raționale

Acest videoclip descrie când o funcție rațională are o asimptotă oblică, descrie pe scurt ce este o asimptotă oblică și apoi face două exemple.

• Show Step-by-step Solutions

Find Asymptotes of a Rational Function (Vertical, Horizontal and Oblique/Slant)

Acest videoclip arată cum să găsim asimptotele verticale și o asimptotă înclinată / oblică a unei funcții raționale.

• Show Step-by-step Solutions

Finding All Asymptotes of a Rational Function (Vertical, Horizontal, Oblique / Slant)

Aici ne uităm la o funcție și găsim asimptota verticală și, de asemenea, concluzionăm că nu există asimptote orizontale, dar că există o asimptotă oblică. Apoi folosim diviziunea lungă pentru a găsi asimptota oblică.

• Arată soluțiile pas cu pas

Încercați calculatorul gratuit Mathway și rezolvatorul de probleme de mai jos pentru a exersa diverse subiecte de matematică. Încercați exemplele date sau introduceți propria problemă și verificați-vă răspunsul cu ajutorul explicațiilor pas cu pas.