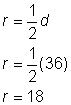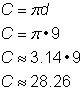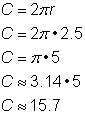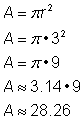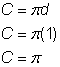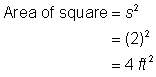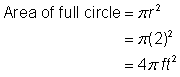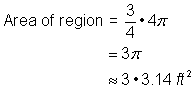Cercuri
Obiectivul (obiectivele) de învățare
– Să identifice proprietățile cercurilor.
– Să găsească circumferința unui cerc.
– Aflați aria unui cerc.
– Aflați aria și perimetrul unor figuri geometrice compuse.
Introducere
Cercurile sunt o formă comună. Le vedeți peste tot – roțile unei mașini, Frisbee-uri care trec prin aer, discuri compacte care livrează date. Toate acestea sunt cercuri.
Un cerc este o figură bidimensională, la fel ca poligoanele și cvadrilateralele. Cu toate acestea, cercurile sunt măsurate diferit față de aceste alte forme – trebuie chiar să folosiți niște termeni diferiți pentru a le descrie. Să aruncăm o privire asupra acestei forme interesante.
Proprietăți ale cercurilor
Un cerc reprezintă un set de puncte, toate aflate la aceeași distanță de un punct fix, din mijloc. Acest punct fix se numește centru. Distanța de la centrul cercului la orice punct de pe cerc se numește rază.
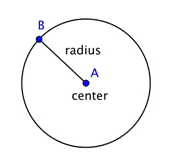
Când două raze (pluralul lui radius) sunt puse împreună pentru a forma un segment de dreaptă care traversează cercul, se obține un diametru. Diametrul unui cerc trece prin centrul cercului și își are extremitățile pe cercul însuși.
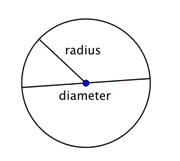
Diametrul oricărui cerc este de două ori lungimea razei acelui cerc. El poate fi reprezentat prin expresia 2r, sau „de două ori raza”. Deci, dacă știți raza unui cerc, o puteți înmulți cu 2 pentru a afla diametrul; acest lucru înseamnă, de asemenea, că dacă știți diametrul unui cerc, îl puteți împărți la 2 pentru a afla raza.
|
Exemplu |
||
|
Problemă |
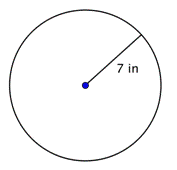
Găsește diametrul cercului.
|
|
|
d = 2r d = 2(7) d = 14 |
Diametrul este de două ori mai mare decât raza, sau 2r. Raza acestui cerc este de 7 inci, deci diametrul este 2(7) = 14 inci. |
|
|
Răspuns |
Diametrul este de 14 inci. |
|
|
Exemplu |
||
|
Problemă |
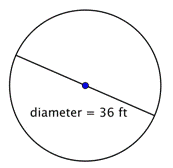
Găsește raza cercului.
|
|
|
|
Raza este jumătate din diametru, adică |
|
|
Răspuns |
Raza este de 18 picioare. |
|
Circumferința
Distanța în jurul unui cerc se numește circumferință. (Reamintim, distanța în jurul unui poligon este perimetrul.)
O proprietate interesantă despre cercuri este aceea că raportul dintre circumferința unui cerc și diametrul său este același pentru toate cercurile. Indiferent de mărimea cercului, raportul dintre circumferință și diametru va fi același.
Câteva măsurători reale ale unor obiecte diferite sunt furnizate mai jos. Măsurătorile sunt exacte cu o precizie de un milimetru sau un sfert de inch (în funcție de unitatea de măsură folosită). Priviți raportul dintre circumferință și diametru pentru fiecare dintre ele – deși articolele sunt diferite, raportul pentru fiecare este aproximativ același.
|
Articolul |
Circumferința (C) (rotunjită la cea mai apropiată sutime) |
.
Diametru (d) |
Raport |
|
|
Cup |
253 mm . |
79 mm |
|
|
|
sfert |
84 mm |
27 mm |
|
|
|
Bowl |
37.25 in |
11.75 in |
|
Circumferința și diametrul sunt măsurători aproximative, deoarece nu există o modalitate precisă de a măsura exact aceste dimensiuni. Cu toate acestea, dacă ați putea să le măsurați mai precis, ați constata că raportul ![]() s-ar apropia de 3,14 pentru fiecare dintre elementele date. Denumirea matematică a raportului
s-ar apropia de 3,14 pentru fiecare dintre elementele date. Denumirea matematică a raportului ![]() este pi și este reprezentată de litera greacă
este pi și este reprezentată de litera greacă ![]() .
.
![]() este o zecimală care nu se termină și nu se repetă, așa că este imposibil să o scriem complet. Primele 10 cifre ale lui
este o zecimală care nu se termină și nu se repetă, așa că este imposibil să o scriem complet. Primele 10 cifre ale lui ![]() sunt 3,141592653; este adesea rotunjit la 3,14 sau estimat ca fracția
sunt 3,141592653; este adesea rotunjit la 3,14 sau estimat ca fracția ![]() . Rețineți că atât 3,14, cât și
. Rețineți că atât 3,14, cât și ![]() sunt aproximări ale lui
sunt aproximări ale lui![]() și sunt folosite în calculele în care nu este important să fie precise.
și sunt folosite în calculele în care nu este important să fie precise.
Din moment ce știți că raportul dintre circumferință și diametru (sau ![]() ) este consecvent pentru toate cercurile, puteți folosi acest număr pentru a găsi circumferința unui cerc dacă îi cunoașteți diametrul.
) este consecvent pentru toate cercurile, puteți folosi acest număr pentru a găsi circumferința unui cerc dacă îi cunoașteți diametrul.
![]() =
= ![]() , deci C =
, deci C = ![]() d
d
De asemenea, deoarece d = 2r, atunci C = ![]() d =
d = ![]() (2r) = 2
(2r) = 2![]() r.
r.
Circumferința unui cerc
Pentru a afla circumferința (C) unui cerc, folosiți una dintre următoarele formule:
Dacă știți diametrul (d) unui cerc: ![]()
Dacă cunoașteți raza (r) unui cerc: ![]()
|
Exemplu |
||
|
Problemă |
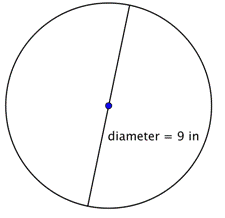
Găsește circumferința cercului.
|
|
|
|
Pentru a calcula circumferința dat fiind un diametru de 9 inci, folosiți formula Din moment ce folosiți o aproximație pentru |
|
|
Răspuns |
Circumferința este 9 |
|
|
Exemplu |
||
|
Problemă |
Găsește circumferința unui cerc cu raza de 2.5 yarzi. |
|
|
|
Pentru a calcula circumferința unui cerc având o rază de 2,5 yarzi, folosiți formula |
|
|
Răspuns |
Circumferința este 5 |
|
Un cerc are o rază de 8 inci. Care este circumferința sa, rotunjită la cel mai apropiat inch?
A) 25 inches
B) 50 inches
C) 64 inci2
D) 201 inci
Arie
![]() este un număr important în geometrie. L-ați folosit deja pentru a calcula circumferința unui cerc. Folosiți
este un număr important în geometrie. L-ați folosit deja pentru a calcula circumferința unui cerc. Folosiți ![]() și atunci când calculați aria unui cerc.
și atunci când calculați aria unui cerc.
Aria unui cerc
Pentru a afla aria (A) unui cerc, folosiți formula: ![]()
|
Exemplu |
||
|
Problemă |
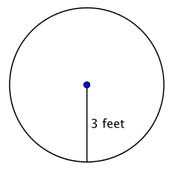
Găsește aria cercului.
|
|
|
|
Pentru a afla aria acestui cerc, folosiți formula Amintiți-vă să scrieți răspunsul în unități pătrate, deoarece găsiți aria. |
|
|
Răspuns |
Aria este 9 |
|
Un nasture are un diametru de 20 milimetri. Care este aria butonului? Folosiți 3,14 ca o aproximare a ![]() .
.
A) 62,8 mm
B) 314 mm2
C) 400 mm2
D) 1256 mm2
Figura compusă
Acum că știți cum să calculați circumferința și aria unui cerc, puteți folosi aceste cunoștințe pentru a găsi perimetrul și aria figurilor compuse. Trucul pentru a rezolva aceste tipuri de probleme este să identificați formele (și părțile de forme) din cadrul figurii compuse, să le calculați dimensiunile individuale și apoi să le adunați.
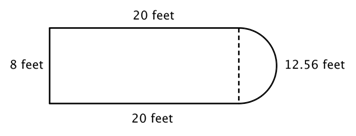
De exemplu, priviți imaginea de mai jos. Este posibil să găsim perimetrul?
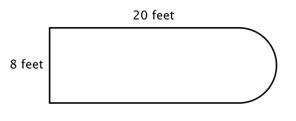
Primul pas este să identificăm figuri mai simple în cadrul acestei figuri compuse. Puteți să o descompuneți într-un dreptunghi și un semicerc, așa cum se arată mai jos.
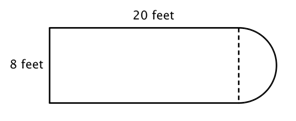
Știți cum să găsiți perimetrul unui dreptunghi și știți cum să găsiți circumferința unui cerc. Aici, perimetrul celor trei laturi pline ale dreptunghiului este 8 + 20 + 20 + 20 = 48 de picioare. (Observați că numai trei laturi ale dreptunghiului se vor adăuga în perimetrul figurii compuse, deoarece cealaltă latură nu se află la o muchie; ea este acoperită de semicerc!)
Pentru a afla circumferința semicercului, folosiți formula ![]() cu un diametru de 8 picioare, apoi luați jumătate din rezultat. Circumferința semicercului este
cu un diametru de 8 picioare, apoi luați jumătate din rezultat. Circumferința semicercului este ![]() , sau aproximativ 12,56 picioare, deci perimetrul total este de aproximativ 60,56 picioare.
, sau aproximativ 12,56 picioare, deci perimetrul total este de aproximativ 60,56 picioare.
|
Exemplu |
||
|
Problemă |
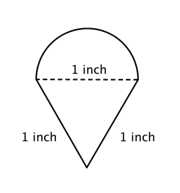
Găsește perimetrul (cu aproximație de o sutime) al figurii compuse, formată dintr-un semicerc și un triunghi.
|
|
|
|
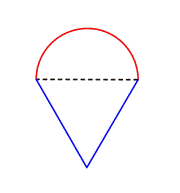
Identificați formele mai mici din interiorul figurii compuse. Această figură conține un semicerc și un triunghi. |
|
|
Diametru (d) = 1
Circumferința semicercului = |
Găsește circumferința cercului. Apoi împărțiți la 2 pentru a afla circumferința semicercului. |
|
|
|
|
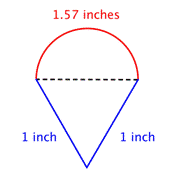
Găsește perimetrul total prin însumarea circumferinței semicercului și a lungimilor celor două picioare. Deoarece măsurarea noastră a circumferinței semicercului este aproximativă, perimetrul va fi, de asemenea, o aproximație. |
|
Răspuns |
Aproximativ 3.57 inch |
|
|
Exemplu |
||
|
Problemă |
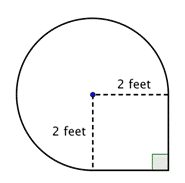
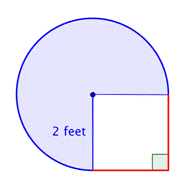
Găsește aria figurii compuse, formată din trei sferturi de cerc și un pătrat, cu o precizie de o sutime.
|
|
|
|
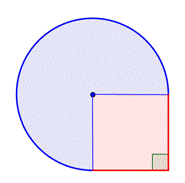
Identificați formele mai mici din interiorul figurii compuse. Această figură conține o regiune circulară și un pătrat. Dacă găsiți aria fiecăreia dintre ele, puteți afla aria întregii figuri. |
|
|
|
Căutați aria pătratului. |
|
|
|
|
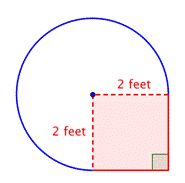
Găsește aria regiunii circulare. Raza este de 2 picioare. Rețineți că regiunea este |
|
|
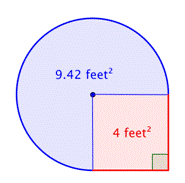
4 picioare2 + |
Adunați cele două regiuni. Deoarece măsurarea suprafeței circularei este aproximativă, suprafața figurii va fi, de asemenea, o aproximație. |
|
Răspuns |
Suprafața este de aproximativ 13.42 picioare2. |
|
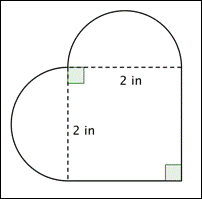
Care este aria (la cea mai apropiată sutime) a figurii prezentate mai jos? (Ambele regiuni rotunjite sunt semicercuri.)
A) 16,56 in2
B) 7,14 in2
C) 4 in2
D) 3.14 in2
Rezumat
Circuitele sunt o formă geometrică importantă. Distanța în jurul unui cerc se numește circumferință, iar spațiul interior al unui cerc se numește arie. Calcularea circumferinței și a ariei unui cerc necesită un număr numit pi (![]() ), care este o zecimală care nu se termină și nu se repetă. Pi este adesea aproximat prin valorile 3,14 și
), care este o zecimală care nu se termină și nu se repetă. Pi este adesea aproximat prin valorile 3,14 și ![]() . Puteți afla perimetrul sau aria formelor compuse – inclusiv a formelor care conțin secțiuni circulare – aplicând formulele circumferinței și ariei, acolo unde este cazul.
. Puteți afla perimetrul sau aria formelor compuse – inclusiv a formelor care conțin secțiuni circulare – aplicând formulele circumferinței și ariei, acolo unde este cazul.
.