Ceea ce urmează este părerea mea despre câteva probleme de matematică din presupusa „matematică de bază comună” sau „noua matematică” care au circulat pe internet. Consider că acestea ne arată o implementare greșită a CCS.
Atenție, nu tot ceea ce vedeți în cărțile de matematică sau pe internet este realizat corect pe baza CCS. În unele dintre exemplele pe care le vedeți, se pare că oamenii aruncă la gunoi bunul simț atunci când fac probleme de matematică pentru a răspunde standardelor de bază comune!
Nu sunt surprins că implementarea a ajuns să fie „ratată” în unele locuri. CCS reprezintă o schimbare atât de mare pentru majoritatea profesorilor, încât aceștia au nevoie de mult sprijin și reeducare înainte de a fi nevoiți să predea conform acestora.
Întotdeauna am crezut că problema PRINCIPALĂ cu care se confruntă educația matematică în clasele primare din școlile publice este că mulți profesori de școală primară nu înțeleg matematica suficient de bine pentru a o putea preda corect chiar și la nivel elementar. De exemplu, mulți dintre ei nu înțeleg conceptele, de ce și pentru ce ale algoritmilor pe care îi predau. Nu este vina lor – problema se trage de la ceea ce au fost învățați în formarea profesorilor și în propria lor școlarizare.
Inclusiv documentul de standarde în sine este oarecum greu de urmărit pe alocuri. Citirea lui necesită o anumită gândire. Mi-aș dori ca cineva să producă o broșură care să explice standardele într-un limbaj simplu și cu numeroase exemple.
Exemple proaste de „common core” sau „noua matematică”
Exemplu 1
Recent am văzut pe Facebook o imagine cu strategii de scădere care pretindea că este dintr-o carte de matematică de clasa I și că este „Common Core math”.”
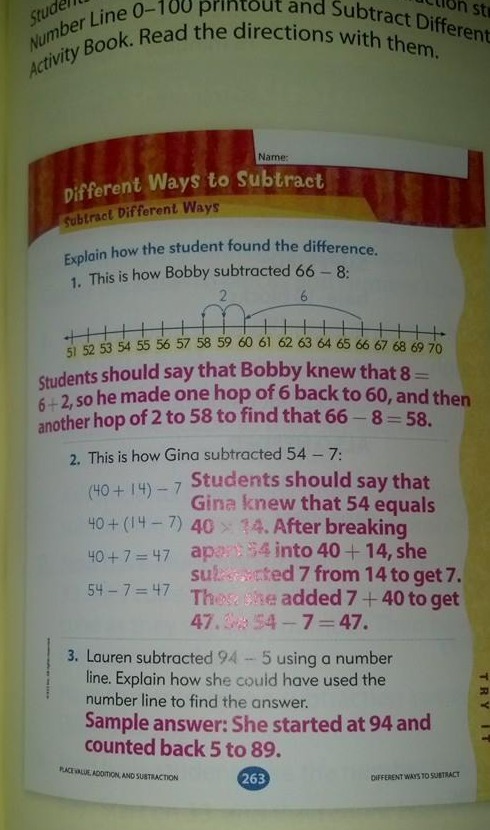
Cred că metoda 2 este mult prea dificilă pentru clasa I și aș lăsa chiar și metoda 1 pentru clasa a II-a.
Chiar dacă acea carte nici măcar nu pare să se alinieze la standardele Common Core. Standardele pentru clasa I pur și simplu nu includ acest tip de probleme de scădere!
Aceasta este ceea ce găsim în standarde:
Adăugare și scădere în limita a 20.
1.OA.5
Relaționează numărarea cu adunarea și scăderea (de exemplu, prin numărarea pe 2 pentru a adăuga 2).
1.OA.6.
Adaugă și scade în limita a 20, demonstrând fluență pentru adunarea șisubstracția în limita a 10. Folosește strategii cum ar fi numărarea de la un număr la altul; realizarea a zece (de exemplu, 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14); descompunerea unui număr care duce la zece (de exemplu, 13 – 4 = 13 – 3 – 1 = 10 – 1 = 9); utilizarea relației dintre adunare și scădere (de exemplu, știind că 8 + 4 = 12, se știe că 12 – 8 = 4); și crearea de sume echivalente, dar mai ușoare sau cunoscute (de ex, adunarea 6 + 7 prin crearea echivalentului cunoscut 6 + 6 + 1 = 12 + 1 = 13).
Exemplul din manualul școlar pare să vrea să abordeze 1.OA.6 de mai sus, dar acesta este în mod clar pentru adunarea și scăderea în limita a 20, nu cu numere mai mari.
Mai târziu, în standardele pentru clasa I, vedem două standarde care au legătură cu scăderea numerelor de două cifre (în limita a 100):
1.NBT.5.
Dat un număr de două cifre, găsiți mental cu 10 mai mult sau cu 10 mai puțin decât numărul, fără a fi nevoie să numărați; explicați raționamentul folosit.
1.NBT.6.
Suprimați multiplii de 10 în intervalul 10-90 din multiplii de 10 în intervalul 10-90 (diferențe pozitive sau zero), folosind modele concrete sau desene și strategii bazate pe valoarea locului, proprietățile operațiilor și/sau relația dintre adunare și scădere; raportați strategia la o metodă scrisă și explicați raționamentul folosit.
Nota Mariei: aceasta înseamnă scăderi precum 34 – 20 sau 89 – 60.
dar niciuna dintre acestea nu include subtrageri precum 54 – 7 sau 82 – 6. Acestea sunt în clasa a 2-a:
2.NBT.5
Să adune și să sustragă fluent în limita a 100 folosind strategii bazate pe valoarea locului, proprietățile operațiilor și/sau relația dintre adunare și scădere.
Rețineți că standardul pentru clasa a II-a nu specifică CUM se face scăderea (dacă se folosesc strategii de matematică mentală sau se scriu numere unul sub altul și se împrumută/se grupează).
Exemplu 2
De la Houghton Mifflin, se presupune:
Juanita vrea să le dea pungi de autocolante prietenilor ei. Ea vrea să dea același număr de autocolante fiecărui prieten. Ea nu este sigură dacă are nevoie de 4 pungi sau de 6 pungi de autocolante. Câte abțibilduri ar putea cumpăra astfel încât să nu mai rămână niciun abțibild?
Problema abțibildurilor are de-a face cu conceptul de cel mai mic multiplu comun (LCM). (Răspunsul este că ea ar trebui să cumpere 12, 24, 36 sau orice alt multiplu de 12 abțibilduri, pentru că astfel le poate împărți fie în 4 pungi, fie în 6 pungi.)
Sigur, problema este FOARTE neclară și prost formulată. Părerea mea este că broșura în care apare acest lucru este pur și simplu needitată. Nu este vina standardelor în sine. Sunt de acord cu Bart Goddard pe Math Forum. Acesta este un simptom al grabei oarbe de a produce probleme de poveste „din viața reală” care sfârșesc prin a fi fără sens.
Din documentul PDF în care apare, concluzionez că problema este pentru clasa a IV-a, deoarece toate celelalte probleme de cuvinte din broșură corespund standardelor pentru clasa a IV-a (factori, numere prime). Dar, CCS nu include nici măcar cel mai mic multiplu comun în standardele pentru clasa a 4-a (este în clasa a 6-a)!!! Ceva a luat-o razna cu adevărat cu această problemă de cuvinte.
Exemplul 3
Încă o dată, se presupune că este de la Houghton Mifflin pentru clasa I. Acesta se potrivește cu standardul pe care l-am citat deja mai sus:
Adăugați și scădeți în limita a 20.
1.OA.6.
Adaugați și scădeți în limita a 20, demonstrând fluență pentru adunări și scăderi în limita a 10. Folosește strategii cum ar fi: numărarea în continuare; realizarea a zece (de exemplu, 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14); descompunerea unui număr care duce la zece (de exemplu, 13 – 4 = 13 – 3 – 1 = 10 – 1 = 9); utilizarea relației dintre adunare și scădere (de ex, știind că 8 + 4 = 12, se știe că 12 – 8 = 4); și crearea unor sume echivalente, dar mai ușoare sau cunoscute (de exemplu, adunarea 6 + 7 prin crearea echivalentului cunoscut 6 + 6 + 1 = 12 + 1 = 13).
Acum, în primul rând, strategia de „a face zece” are legătură cu ADĂUGAREA, nu cu scăderea. În cazul scăderii, se numește „descompunerea unui număr care duce la zece”. Așadar, instrucțiunile ar trebui să spună: „Care arată o modalitate de a descompune un număr care duce la zece?”. Consider că este o prostie totală să le cerem elevilor de clasa I să cunoască o astfel de terminologie.
Dar mai este o problemă aici. Dacă citiți cu adevărat toate standardele, veți observa că în alte câteva locuri li se cere elevilor să explice raționamentul folosit sau să relaționeze o anumită metodă vizuală cu strategia, dar NU în acest standard!
După cum văd eu acest standard, profesorii ar trebui să ÎNVĂȚE diversele trategii menționate și apoi să le dea elevilor probleme SIMPLE de adunare și scădere în limita a 20, cum ar fi 15 – 8 și 10 – 6. NU văd că acest standard le cere elevilor să recunoască dacă un anumit model vizual corespunde unei anumite strategii.
Din nou, se pare că autorul aruncă la gunoi bunul simț… și nu înțelege de fapt standardele.
Exemplul 4
Exemplul de mai jos este foarte prost formulat, dar CONCEPTUL din spatele lui este foarte bun și se găsește și în Math Mammoth. Prin urmare, îmi pot da seama ce vor.
Vezi cinci pătrate. Colorează unele în albastru și restul în roșu. Asta e clar.
Colorați apoi pătratele din „legătura numerică” în același mod. Legătura numerică merge la aceste trei cercuri. Un copil care a fost prezent la o lecție în care profesorul predă legăturile numerice știe, sperăm, ce înseamnă acest lucru. Este același concept ca o familie de fapte… numărul de sus este suma sau totalul (5), iar numerele care merg la cercurile de jos corespund la câte ai colorat în albastru și câte în roșu, în acest caz 1 și 4.
Apoi cred că partenerii ascunși sunt tot 1 și 4. Arătați degetele 1 și 4 unui adult. În cele din urmă colorați degetele 1 și 4 din imagine (și nu propriile degete cum se pare).
În opinia mea partea cu degetele este superfloare și confuză. Cu toate acestea, conceptul de legături numerice este mult mai vechi decât CCS. Legăturile numerice nu sunt de fapt menționate în CCS, deși se leagă de acest standard:
1.OA.4
Înțelegeți scăderea ca o problemă de adunare necunoscută. De exemplu, scade 10 – 8 prin găsirea numărului care face 10 atunci când este adăugat la 8.
și cu acesta
1.OA.6.
Adaugați și scădeți în limita a 20, demonstrând fluență pentru adunare și scădere în limita a 10.
Nu știu de ce acea fișă de lucru cu legături numerice este dată ca exemplu de Common Core Math. Ar fi mult mai bine intitulată ca un exemplu de fișă de lucru de matematică prost formulată care POATE data chiar de dinainte de Common Core (și care este doar reutilizată în acest curriculum particular)… pentru că, așa cum am spus, legăturile numerice NU sunt menționate în CCS.
Ce nu sunt standardele de matematică din Common Core
- Nu sunt „matematică nouă”. În comparație cu multe programe de matematică folosite în anii 2000, care puneau accentul pe algoritmi netradiționali, CCS reprezintă o mișcare clară către algoritmi tradiționali și memorare. Consultați aceste standarde specifice:
2.OA.2
Adaugați și scădeți fluent în limita a 20 folosind strategii mentale. Până la sfârșitul clasei a 2-a, să știe din memorie toate sumele a două numere de o cifră.
Nota Mariei: acestea sunt faptele de bază ale adunării, cum ar fi 7 + 7 sau 5 + 4.3.OA.7
Înmulțițiți și împărțiți fluent în limita a 100, folosind strategii cum ar fi relația dintre înmulțire și împărțire (de exemplu, știind că 8 × 5 = 40, se știe că 40 ÷ 5 = 8) sau proprietățile operațiilor. Până la sfârșitul clasei a 3-a, să cunoască din memorie toți produsele a două numere de o cifră.
Nota Mariei: aceasta înseamnă tabele de înmulțire și fapte de bază de împărțire.4.NBT.4
Să adune și să sustragă fluent numere întregi de mai multe cifre folosind algoritmul standard.5.NBT.5
Să înmulțească fluent numere întregi de mai multe cifre folosind algoritmul standard.
Nota Mariei: aceasta nu înseamnă că elevii înmulțesc numere întregi de mai multe cifre doar în clasa a V-a; acest lucru este studiat și în clasele a III-a și a IV-a. - Standardele nu impun profesorilor și elevilor strategii ciudate sau modele vizuale. Multe standarde lasă la latitudinea profesorilor și elevilor. De exemplu:
2.NBT.5
Să adune și să sustragă în mod fluent în limita a 100 folosind strategii bazate pe valoarea locului, pe proprietățile operațiilor și/sau pe relația dintre adunare și scădere.Rețineți „și/sau” în propoziția de mai sus. Aceasta înseamnă că profesorii și elevii NU sunt limitați la utilizarea unor strategii specifice și nici nu li se spune să utilizeze mai multe strategii. Algoritmul tradițional de „împrumut” este o strategie bazată pe valoarea locului, așa că este inclusă chiar aici în 2.NBT.5.
2.NBT.9
Explicați de ce funcționează strategiile de adunare și scădere, folosind valoarea loculuiși proprietățile operațiilor. Explicațiile pot fi susținute de desene sau obiecte.Dice „pot fi susținute de desene”, dar nu vă obligă să faceți acest lucru și nici nu vă limitează la utilizarea unui anumit model vizual sau tip de desen.
3.OA.3
Utilizează înmulțirea și împărțirea în limita a 100 pentru a rezolva probleme de tip word insituții care implică grupuri egale, tablouri și mărimi de măsură,de exemplu, folosind desene și ecuații cu un simbol pentru numărul necunoscut pentru a reprezenta problema.Elevul nu TREBUIE să folosească un desen. Acesta este doar menționat ca o posibilitate.
4.NBT.5
Multiplicați un număr întreg de până la patru cifre cu un număr întreg de o cifră și multiplicați două numere de două cifre, folosind strategii bazate pe valoarea locului și pe proprietățile operațiilor. Ilustrați și explicați calculul folosind ecuații, matrice dreptunghiulară, și/sau modele de suprafață.Rețineți „și/sau”. Ilustrează calculul, dar este suficient să îl ilustreze folosind ecuații. Nu TREBUIE să îl ilustrați folosind matrici.
Acestea fiind spuse, unele standarde menționează un model vizual specific, cum ar fi o linie numerică sau un model de arie dreptunghiulară, dar acest lucru este mai puțin frecvent decât să oferiți o alegere ca în standardele de mai sus.
Matematică conceptuală
Există unele standarde care abordează latura conceptuală a matematicii pe care profesorii de școală primară ar putea să nu le înțeleagă dacă nu sunt învățați ce înseamnă; de exemplu:
5. NF.7b
Interpretați împărțirea unui număr întreg la o fracție unitară și calculați astfel de cupluri. De exemplu, creați un context de poveste pentru 4 ÷ (1/5) și folosiți un model vizual de fracție pentru a arăta cuplul. Folosiți relația dintre înmulțire și împărțire pentru a explica faptul că 4 ÷ (1/5) = 20, deoarece 20 × (1/5) = 4.
O astfel de problemă de poveste ar fi: câte bucăți care au lungimea de 1/5 de metru puteți tăia dintr-o bucată de material de 1,5 metri? Un model vizual ar putea arăta 4 întregi, împărțite în cincimi. Putem apoi să numărăm că 4 întregi au un total de 20 de cincimi.
5.NF.4b
Căutați aria unui dreptunghi cu lungimi de latură fracționară prin așezarea acestuia cu pătrate unitare cu lungimi de latură de fracție unitară corespunzătoare și arătați că aria este aceeași cu cea care ar fi obținută prin înmulțirea lungimilor de latură. Înmulțiți lungimile fracționare ale laturilor pentru a găsi suprafețele dreptunghiurilor și reprezentați produsele fracțiunilor ca suprafețe dreptunghiulare.
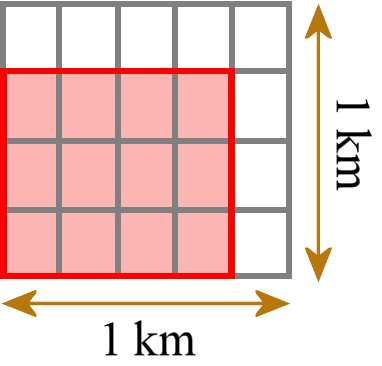Acest lucru înseamnă, de exemplu, un dreptunghi cu lungimi ale laturilor de 3/4 km și 4/5 km. Apoi îl acoperim cu mici dreptunghiuri unitare (nu pătrate unitare; aici standardul însuși are o terminologie greșită) care au fiecare laturile cu lungimi de 1/4 km și 1/5 km.
Putem număra câte mici dreptunghiuri avem nevoie. Avem nevoie de 12 astfel de plăcuțe. Fiecare plăcuță are o suprafață de 1/20 km2, deci suprafața totală este de 12/20 km2. Apoi verificăm și comparăm că obținem același răspuns ca și cum am fi înmulțit cele două lungimi ale laturilor folosind înmulțirea obișnuită a fracțiilor (3/4 km × 4/5 km = 12/20 km2).
Întotdeauna am avut acest tip de probleme în cărțile mele – chiar înainte de apariția CCS.
Unii oameni susțin că copiii nu au nevoie de o astfel de înțelegere conceptuală sau că este prea dificilă. Personal, nu sunt de acord. Întotdeauna (și înainte de CCS) m-am străduit să explic conceptele aritmeticii fracțiilor, astfel încât elevii să nu ajungă să „urmeze orbește regulile”, capabili să calculeze cu fracții doar dacă se întâmplă să-și amintească corect regula. Întotdeauna am pus accentul pe înțelegerea conceptuală în matematică (după cum știu cititorii mei!).
Dar, sper că puteți vedea cum unele dintre aceste lucruri pot fi necunoscute pentru profesorii școlari și părinți și, prin urmare, nu este de mirare că urmărirea standardelor Common Core este dificilă pentru ei.
Speranța mea este că Math Mammoth Light Blue Series și unitățile pe care le vând în magazinele mele Teachers Pay Teachers și Teachers’ Notebook îi pot ajuta pe acei profesori & părinți care au nevoie de materiale aliniate la Common Core. Și, așa cum am spus, restul dintre voi puteți fi încrezători în utilizarea lor, de asemenea. Ele nu conțin nicio matematică „ciudată” sau fără sens, ci, ca întotdeauna, se bazează pur și simplu pe fundamentul solid al predării conceptelor de matematică împreună cu procedurile.
De Maria Miller