Imaginează-ți un pătrat de hârtie întins pe birou. Vă rog să închideți ochii. Auziți cum se deplasează hârtia. Când deschideți ochii, hârtia nu pare să se fi schimbat. Ce aș fi putut să-i fac în timp ce nu vă uitați?
Este evident că nu am rotit hârtia cu 30 de grade, pentru că atunci hârtia ar arăta diferit.

De asemenea, nu am răsturnat-o peste o linie care leagă, să zicem, unul dintre colțuri de punctul median al unei alte muchii. Hârtia ar fi arătat diferit dacă aș fi făcut-o.

Ceea ce aș fi putut face, totuși, ar fi fost să rotesc hârtia în sensul acelor de ceasornic sau în sens invers cu orice multiplu de 90 de grade, sau să o întorc peste oricare dintre liniile diagonale sau peste liniile orizontale și verticale.
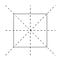
Un mod util de a vizualiza transformările este de a marca colțurile pătratului.

Ultima opțiune este aceea de a nu face nimic. Aceasta se numește transformarea identității. Împreună, toate acestea se numesc transformări de simetrie ale pătratului.
Pot combina transformări de simetrie pentru a face alte transformări de simetrie. De exemplu, două răsturnări peste segmentul de dreaptă BD produc identitatea, la fel ca și patru rotații succesive de 90 de grade în sens invers acelor de ceasornic. O întoarcere în jurul liniei verticale urmată de o întoarcere în jurul liniei orizontale are efectul sigur ca o rotație de 180 de grade. În general, orice combinație de transformări de simetrie va produce o transformare de simetrie. Tabelul de mai jos prezintă regulile de compunere a transformărilor de simetrie:

În acest tabel, R cu indicele 90, 180 și 270 denotă rotații în sens invers acelor de ceasornic cu 90, 180 și 270 de grade, H înseamnă o răsturnare în jurul liniei orizontale, V este o răsturnare în jurul liniei verticale, MD este o răsturnare în jurul diagonalei de la stânga sus la dreapta jos, iar OD înseamnă o răsturnare pe cealaltă diagonală. Pentru a afla produsul dintre A și B, treceți la rândul lui A și apoi la coloana lui B. De exemplu, H∘MD=R₉₀.
Există câteva lucruri pe care le puteți observa uitându-vă la tabel:
- Operația ∘ este asociativă, ceea ce înseamnă că A∘(B∘C) = (A∘B)∘C pentru orice transformări A, B și C.
- Pentru orice pereche de transformări de simetrie A și B, compoziția A∘B este, de asemenea, o transformare de simetrie
- Există un element e astfel încât A∘e=e∘A pentru orice A
- Pentru orice transformare de simetrie A, există o singură transformare de simetrie A-¹ astfel încât A∘A-¹=A-¹∘A=e
Prin urmare, spunem că ansamblul transformărilor de simetrie ale unui pătrat, combinat cu compoziția, formează o structură matematică numită grup. Acest grup se numește D₄, grupul diedru pentru pătrat. Aceste structuri sunt subiectul acestui articol.
Definiția unui grup
Un grup ⟨G,*⟩ este un ansamblu G cu o regulă * pentru combinarea oricăror două elemente din G care satisface axiomele de grup:
În abstract, deseori suprimăm * și scriem a*b ca ab și ne referim la * ca înmulțire.

Nu este necesar ca * să fie comutativ, ceea ce înseamnă că a*b=b*a. Puteți vedea acest lucru uitându-vă la tabelul lui D₄, unde H∘MD=R₉₀ dar MD∘H=R₂₇₀. Grupurile în care * este comutativ se numesc grupuri abeliene după Neils Abel.
Grupurile abeliene sunt mai degrabă excepția decât regula. Un alt exemplu de grup non-abelian este reprezentat de transformările de simetrie ale unui cub. Să considerăm doar rotirile în jurul axelor:
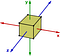
Dacă voi roti mai întâi 90 de grade în sens invers acelor de ceasornic în jurul axei y și apoi 90 de grade în sens invers acelor de ceasornic în jurul axei z, atunci rezultatul său va fi diferit decât dacă aș roti 90 de grade în jurul axei z și apoi 90 de grade în jurul axei y.

Este posibil ca un element să fie propriul său invers. Să considerăm grupul care este format din 0 și 1 cu operația de adunare binară. Tabelul său este:

Este clar că 1 este propriul său invers. Acesta este, de asemenea, un grup abelian. Nu vă faceți griji, majoritatea grupurilor nu sunt atât de plictisitoare.
Câteva alte exemple de grupuri includ:
- Asamblul numerelor întregi cu adunare.
- Asamblul numerelor raționale care nu includ 0 cu înmulțire.
- Asamblul soluțiilor ecuației polinomiale xⁿ-1=0, numite a n-a rădăcină a unității, cu înmulțire.
Iată câteva exemple care nu sunt grupuri:
- Asamblul numerelor naturale supuse adunării nu este un grup, deoarece nu există inverse, care ar fi numerele negative.
- Asamblul tuturor numerelor raționale inclusiv 0 cu înmulțire nu este un grup deoarece nu există un număr rațional q pentru care 0/q=1, deci nu fiecare element are un invers.
Structura grupurilor
Un grup este mult mai mult decât o simplă pată care satisface cele patru axiome. Un grup poate avea o structură internă, iar această structură poate fi foarte complexă. Una dintre problemele de bază în algebra abstractă este de a determina cum arată structura internă a unui grup, deoarece în lumea reală grupurile care sunt studiate efectiv sunt mult mai mari și mai complicate decât exemplele simple pe care le-am dat aici.
Unul dintre tipurile de bază de structură internă este un subgrup. Un grup G are un subgrup H atunci când H este un subansamblu al lui G și:
- Pentru a,b∈H, a*b∈H și b*a∈H
- Pentru a∈H, a-¹∈H
- Identitatea este un element al lui H
Dacă H≠G atunci se spune că H este un subgrup propriu-zis. Subgrupul lui G format numai din identitate se numește subgrup trivial.
Un grup neabelian poate avea subgrupuri comutative. Să considerăm grupul diedru pătrat pe care l-am discutat în introducere. Acest grup nu este abelian, dar subgrupul de rotații este abelian și ciclic:
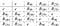
Dăm acum două exemple de structură de grup.
Chiar dacă un grup G nu este abelian, se poate întâmpla totuși să existe o colecție de elemente ale lui G care comută cu tot ce există în G. Această colecție se numește centrul lui G. Centrul C este un subgrup al lui G. Demonstrație:
Să presupunem acum că f este o funcție al cărei domeniu și domeniu sunt ambele G. O perioadă a lui f este un element a∈G astfel încât f(x)=f(ax) pentru tot x∈G. Ansamblul P al perioadelor lui f este un subgrup al lui G. Demonstrație:
Grupurile finite sunt finit generate
Am văzut că grupurile ciclice sunt generate de un singur element. Atunci când este posibil să scriem fiecare element al unui grup G ca produse ale unui subansamblu (nu neapărat propriu) A din G, atunci spunem că A generează G și scriem acest lucru sub forma G=⟨A⟩. Cea mai „well, duh” dovadă pe care o veți vedea vreodată este dovada că toate grupurile finite sunt generate de un ansamblu generator finit:
- Să fie G finit. Fiecare element al lui G este un produs al altor două elemente ale lui G, deci G=⟨G⟩. QED.

Vom încheia acest articol cu o aplicație.
Comunicare rezistentă la erori
Cel mai simplu mod de a transmite informații digitale este de a le codifica în șiruri binare de lungime fixă. Nici o schemă de comunicare nu este complet lipsită de interferențe, astfel încât există întotdeauna posibilitatea ca datele greșite să fie recepționate. Metoda de decodare cu probabilitate maximă este o abordare simplă și eficientă pentru detectarea și corectarea erorilor de transmisie.
Să fie 𝔹ⁿ setul de șiruri binare, sau cuvinte, de lungime n. Este simplu de demonstrat că 𝔹ⁿ este un grup abelian sub adunare binară fără portare (astfel încât, de exemplu, 010+011=001). Rețineți că fiecare element este propriul său invers. Un cod C este un subansamblu al lui 𝔹ⁿ. Următorul este un exemplu de cod în 𝔹⁶:
C = {000000, 001011, 010110, 011101, 100101, 101110, 110011, 111000}
Elementele unui cod se numesc cuvinte de cod. Numai cuvintele de cod vor fi transmise. Se spune că apare o eroare atunci când o interferență modifică un bit dintr-un cuvânt transmis. Distanța d(a,b) dintre două cuvinte de cod a și b este numărul de cifre în care diferă două cuvinte de cod. Distanța minimă a unui cod este cea mai mică distanță dintre oricare două dintre cuvintele sale de cod. Pentru exemplul de cod de mai sus, distanța minimă este trei.
În metoda de decodare cu probabilitate maximă, dacă primim un cuvânt x, care poate conține erori, receptorul trebuie să interpreteze x ca fiind cuvântul de cod a astfel încât d(a,x) să fie minimă. Voi arăta că, pentru un cod cu distanța minimă m, aceasta poate întotdeauna (1) să detecteze erorile care modifică mai puțin de m biți și (2) să corecteze erorile care modifică ½(m-1) sau mai puțini biți.

În exemplul nostru de cod, m=3 și sfera de rază ½(m-1)=1 în jurul cuvântului de cod 011101 este {011101, 111101, 111101, 001101, 011001, 010101, 01111111, 011100}. Deci, dacă receptorul primește oricare dintre aceste cuvinte, el știe că trebuia să primească 011101.
Așa că toate acestea sunt bune și frumoase, dar ce legătură au toate acestea cu teoria grupurilor? Răspunsul se află în modul în care producem de fapt codurile cu care lucrează această metodă.
Este posibil ca un cod din 𝔹ⁿ să formeze un subgrup. În acest caz spunem că acel cod este un cod de grup. Codurile de grup sunt grupuri finite, deci sunt finit generate. Vom vedea cum să producem un cod prin găsirea unui ansamblu generator.
Un cod poate fi specificat astfel încât primii câțiva biți din fiecare cuvânt de cod să fie numiți biți de informație, iar biții de la sfârșit să fie numiți biți de paritate. În exemplul nostru de cod C, primii trei biți sunt biți de informație și ultimii trei sunt biți de paritate. Biții de paritate satisfac ecuațiile de verificare a parității. Pentru un cuvânt de cod A₁A₂A₃A₄A₅A₆, ecuațiile de paritate sunt A₄=A₁+A₂, A₅=A₂+A₃ și A₆=A₁+A₃. Ecuațiile de paritate oferă un alt nivel de protecție împotriva erorilor: dacă oricare dintre ecuațiile de paritate nu este satisfăcută, atunci s-a produs o eroare.
Iată ce facem. Să presupunem că dorim cuvinte de cod cu m biți de informație și n biți de paritate. Pentru a genera un cod de grup, scrieți o matrice cu m rânduri și m+n coloane. În blocul format de primele m coloane, scrieți matricea identitate m×m. În coloana j pentru m+1≤j≤m_n, scrieți un 1 în al k-lea rând dacă Aₖ apare în ecuația de paritate pentru bitul de paritate Aⱼ și 0 în caz contrar. În exemplul nostru de cod, matricea este:

O astfel de matrice se numește matrice generatoare pentru codul de grup. Se poate verifica direct că rândurile generează C:

Rândurile oricărei matrice generatoare formează un ansamblu generator pentru un cod de grup C. Demonstrație:
- Identitate și inverse: Orice rând adăugat la el însuși dă identitatea, un șir format din toate zerourile.
- Cercetare: Dacă A,B∈C atunci A și B sunt sume de rânduri ale matricei generatoare, deci A+B este de asemenea o sumă de rânduri ale matricei generatoare. Prin urmare A+B∈C.
Aceasta ne permite să generăm un cod, acum voi arăta cum să generăm un cod util.
Definiți greutatea w(x) ca însemnând numărul de unu din x. De exemplu, w(100101)=3. Este evident că w(x)=d(x,0) unde 0 este un cuvânt ale cărui cifre sunt toate zerouri. Greutatea minimă W a unui cod este greutatea cuvântului de cod diferit de zero cu cei mai puțini unu din cod. Pentru un cod de distanță minimă m, d(x,0)≥m deci w(x)≥m și, prin urmare, W=m.
Reamintim că pentru ca un cuvânt să fie considerat cuvânt de cod, trebuie să satisfacă un set de ecuații de verificare a parității. Pentru exemplul nostru de cod, acestea sunt A₄=A₁+A₂, A₅=A₂+A₃, și A₆=A₁+A₃. Putem, de asemenea, să le scriem ca un sistem liniar:
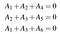
Care la rândul său poate fi scris în termeni de produse de puncte:

Sau într-o formă mai compactă ca Ha=0 unde a=(A₁,A₂,A₂,A₃,A₄,A₅,A₆) și H este matricea de verificare a parității pentru cod:

Se poate verifica prin calcul direct că dacă w(a)≤2 atunci nu putem avea Ha=0. În general, ponderea minimă este t+1, unde t este cel mai mic număr astfel încât orice colecție de t coloane din H să nu însumeze zero (adică să fie liniar independente). Demonstrarea acestui lucru ne-ar duce un pic prea departe în algebra liniară.
Dacă asta vă sperie, nu vă faceți griji. Putem produce niște coduri foarte bune fără ea, profitând de faptul că rezultatul pe care tocmai l-am menționat implică faptul că, dacă fiecare coloană din H este diferită de zero și nu există două coloane egale, atunci greutatea minimă și, prin urmare, distanța minimă a codului, este de cel puțin trei. Acest lucru este foarte bun: dacă se așteaptă ca sistemul nostru de comunicații să aibă o eroare de un bit la fiecare sută de cuvinte transmise, atunci doar unul din zece mii de cuvinte transmise va avea o eroare necorectată și unul din un milion de cuvinte transmise va avea o eroare nedetectată.
Acum avem o rețetă pentru producerea unui cod util pentru schema de detecție cu probabilitate maximă pentru cuvinte de cod care conțin m biți de informație și n biți de paritate:
- Crearea unei matrice cu m+n coloane și n rânduri. Completați matricea cu unu și zerouri astfel încât nici două coloane să nu fie identice și nici o coloană să nu aibă doar zerouri.
- Cărui rând al matricei de verificare a parității rezultate îi corespunde una dintre ecuațiile biților de paritate. Scrieți-le sub forma unui sistem de ecuații și rezolvați-le astfel încât fiecare bit de paritate să fie scris în funcție de biții de informație.
- Creați o matrice cu m+n coloane și m rânduri. În blocul format de primele m coloane, scrieți matricea identitate m×m. În coloana j pentru m+1≤j≤m_n, scrieți un 1 în al k-lea rând dacă Aₖ apare în ecuația de paritate pentru bitul de paritate Aⱼ și 0 în caz contrar.
- Rândurile acestei matrice sunt generatoarele unui grup de coduri cu distanța minimă de cel puțin trei. Acesta este codul pe care îl vom folosi.
Ca exemplu, să presupunem că am nevoie de un cod simplu, de opt cuvinte și că am nevoie doar de o detecție de bază a erorilor și nu de corecție, deci pot scăpa cu o distanță minimă de doi. Vreau trei biți de informație și doi biți de paritate. Scriu următoarea matrice de verificare a parității:
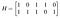
Există două perechi de coloane care sunt egale, astfel încât cel mai mic t pentru care orice colecție de t coloane este liniar independentă este unu, deci greutatea minimă și, prin urmare, distanța minimă pe care o voi avea, este doi. Rândurile reprezintă ecuațiile de verificare a parității A₄=A₁+A₃ și A₅=A₁+A₂+A₃. Matricea mea generatoare este deci:

Și rândurile acestei matrice generează grupul de coduri:
- {00000, 00111, 01001, 01110, 10011, 10100, 111010, 11101}
Observații de încheiere
Algebra abstractă este un subiect profund, cu implicații de anvergură, dar și foarte ușor de învățat. În afară de câteva mențiuni trecătoare de algebră liniară, aproape tot ceea ce am discutat aici este accesibil cuiva care a avut doar algebră de liceu.
Când mi-a venit ideea de a scrie acest articol am vrut neapărat să vorbesc despre cubul Rubik, dar în cele din urmă am vrut să aleg un exemplu care să poată fi acoperit doar cu cele mai elementare idei din teoria grupurilor. În plus, sunt atât de multe de spus despre grupul cubului lui Rubik încât merită un articol de sine stătător, așa că acesta va apărea în curând.
Cursurile mele de la facultate de algebră abstractă s-au bazat pe cartea A Book of Abstract Algebra de Charles Pinter, care este și o tratare accesibilă. Exemplele din acest articol au fost toate împrumutate cu unele modificări de la Pinter.
Ca o notă finală, toate imaginile care nu sunt citate sunt opera mea originală și pot fi folosite cu atribuire. Ca întotdeauna, apreciez orice corecții sau cereri de clarificare.
.